Assessment and Improvement of Global Gridded Sea Surface Temperature Datasets in the Yellow Sea Using In Situ Ocean Buoy and Research Vessel Observations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Satellite SST Products
2.2. In Situ SST Data in the Yellow Sea
2.3. Bias Correction Method of the L4 SST Products
2.4. OSTIA SST Interpolation Scheme
3. Results
3.1. Comparison with In Situ SST Observations
3.2. Spatial and Temporal Variations of the SST RMSD
3.2.1. Spatial Distribution of the SST RMSD
3.2.2. Seasonal Variation of the RMSD and Bias
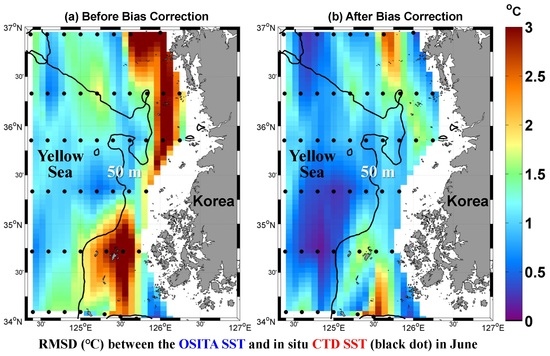
3.3. Bias Correction of the L4 SST Products in the YS
4. Discussion
4.1. Spatial Pattern of Warm Bias in the Shallow Region
4.2. Sea Fog Formation in the Eastern YS
4.3. Availabily of a L3 SST in the YS
4.4. Background and Covariances Used for the Optimal Interpolation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- O’Carroll, A.G.; Armstrong, E.M.; Beggs, H.M.; Bouali, M.; Casey, K.S.; Corlett, G.K.; Dash, P.; Donlon, C.J.; Gentemann, C.L.; Hoeyer, J.; et al. Observational needs of sea surface temperature. Front. Mar. Sci. 2019, 6, 420. [Google Scholar] [CrossRef]
- Kwon, K.M.; Choi, B.-J.; Lee, S.-H.; Kim, Y.H.; Seo, G.-H.; Cho, Y.-K. Effect of model error representation in the Yellow and East China Sea modeling system based on the ensemble Kalman filter. Ocean Dyn. 2016, 66, 263–283. [Google Scholar] [CrossRef]
- Kwon, K.; Choi, B.-J.; Lee, S.-H. Assimilation of different SST datasets to a coastal ocean modeling system in the Yellow and East China Sea. J. Coast. Res. 2018, 85, 1041–1045. [Google Scholar] [CrossRef]
- Browne, P.; Rosnay, P.D.; Zuo, H.; Bennett, A.; Dawson, A. Weakly coupled ocean–atmosphere data assimilation in the ECMWF NWP system. Remote Sens. 2019, 11, 234. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.-P. Ocean–atmosphere interaction and tropical climate. In Tropical Meteorology; Wang, Y., Ed.; The Encyclopedia of Life Support Systems (EOLSS): Paris, France, 2009; pp. 189–201. [Google Scholar]
- Martin, M.; Dash, P.; Ignatov, A.; Banzon, V.; Beggs, H.; Brasnett, B.; Cayula, J.-F.; Cummings, J.; Donlon, C.; Gentemann, C.; et al. Group for high resolution sea surface temperature (GHRSST) analysis fields inter-comparisons. Part 1: A GHRSST multi-product ensemble (GMPE). Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 21–30. [Google Scholar]
- Dash, P.; Ignatov, A.; Martin, M.; Donlon, C.; Brasnett, B.; Reynolds, R.W.; Banzon, V.; Beggs, H.; Cayula, J.F.; Chao, Y.; et al. Group for high resolution sea surface temperature (GHRSST) analysis fields inter-comparisons. Part 2: Near real time web-based Level 4 SST quality monitor (L4-SQUAM). Deep Sea Res. Part II Top. Stud. Oceanogr. 2012, 77, 31–43. [Google Scholar]
- Xie, J.; Zhu, J.; Yan, L. Assessment and inter-comparison of five high-resolution sea surface temperature products in the shelf and coastal seas around China. Cont. Shelf Res. 2008, 28, 1286–1293. [Google Scholar] [CrossRef]
- Castro, S.L.; Wick, G.A.; Steele, M. Validation of satellite sea surface temperature analyses in the Beaufort Sea using UpTempO buoys. Remote Sens. Environ. 2016, 187, 458–475. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite SST analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Zhang, H.-M.; Smith, T.M.; Gentemann, C.L.; Wentz, F. Impacts of in situ and additional satellite data on the accuracy of a sea-surface temperature analysis for climate. Int. J. Clim. 2005, 25, 857–864. [Google Scholar] [CrossRef]
- Pisano, A.; Nardelli, B.B.; Tronconi, C.; Santoleri, R. The new Mediterranean optimally interpolated pathfinder AVHRR SST dataset (1982–2012). Remote Sens. Environ. 2016, 176, 107–116. [Google Scholar] [CrossRef]
- Ding, Y.; Chan, J.C.L. The East Asian summer monsoon: An overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar]
- Cho, Y.-K.; Kim, M.-O.; Kim, B.-C. Sea fog around the Korean peninsula. J. Appl. Meteor. 2000, 39, 2473–2479. [Google Scholar]
- Fu, G.; Guo, J.; Xie, S.-P.; Duan, Y.; Zhang, M. Analysis and high-resolution modeling of a dense sea fog event over the Yellow Sea. Atmos. Res. 2006, 81, 293–303. [Google Scholar] [CrossRef]
- Gao, S.H.; Lin, H.; Shen, B.; Fu, G. A heavy sea fog event over the Yellow Sea in March 2005: Analysis and numerical modeling. Adv. Atmos. Sci. 2007, 24, 65–81. [Google Scholar]
- Zhang, H.M.; Reynolds, R.W.; Lumpkin, R.; Molinari, R.; Arzayus, K.; Johnson, M.; Smith, T.M. An integrated global observing system for sea surface temperature using satellites and in situ data: Research to operations. Bull. Am. Meteorol. Soc. 2009, 90, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Seo, G.-H.; Cho, Y.-K.; Choi, B.-J. Variations of heat transport in the northwestern Pacific marginal seas inferred from high-resolution reanalysis. Prog. Oceanogr. 2014, 121, 98–108. [Google Scholar] [CrossRef]
- Seo, G.-H.; Choi, B.-J.; Cho, Y.-K.; Kim, Y.H.; Kim, S. Evaluation of a regional ocean reanalysis system for the east Asian marginal seas based on the ensemble Kalman filter. Ocean Sci. J. 2015, 50, 29–48. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, C.; Shang, S. Validation and inter-comparison of multi-satellite merged sea surface temperature products in the South China Sea and its adjacent waters. J. Remote Sens. 2015, 19, 328–338. (In Chinese) [Google Scholar]
- Kim, E.J.; Kang, S.K.; Jang, S.T.; Lee, J.H.; Kim, Y.H.; Kang, H.W.; Kwon, Y.Y.; Seung, Y.H. Satellite-derived SST validation based on in-situ data during summer in the East China Sea and western North Pacific. Ocean Sci. J. 2010, 45, 159–170. [Google Scholar] [CrossRef]
- Donlon, C.J.; Nightingale, T.J.; Sheasby, T.; Turner, J.; Robinson, I.S.; Emery, W.J. Implications of the oceanic thermal skin temperature deviation at high wind speeds. Geophys. Res. Lett. 1999, 26, 2505–2508. [Google Scholar] [CrossRef]
- Donlon, C.J.; Minnett, P.J.; Gentemann, C.; Nightingale, T.J.; Barton, I.J.; Ward, B.; Murray, M.J. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 2002, 15, 353–369. [Google Scholar] [CrossRef] [Green Version]
- Barton, I.J. Interpretation of satellite-derived sea surface temperatures. Adv. Space Res. 2001, 28, 165–170. [Google Scholar] [CrossRef]
- Murray, M.J.; Allen, M.R.; Merchant, C.J.; Harris, A.R.; Donlon, C.J. Direct observations of skin-depth SST variability. Geophys. Res. Lett. 2000, 27, 1171–1174. [Google Scholar] [CrossRef] [Green Version]
- Kwak, M.-T.; Seo, G.-H.; Cho, Y.-K.; Kim, B.-G.; You, S.H.; Seo, J.-W. Long-term Comparison of satellite and in-situ sea surface temperatures around the Korean Peninsula. Ocean Sci. J. 2015, 50, 109–117. [Google Scholar]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.C.; Schlax, M.G. Daily high-resolution blended analyses for sea surface temperature. J. Clim. 2007, 23, 5473–5496. [Google Scholar] [CrossRef]
- Kurihara, Y.; Sakurai, T.; Kuragano, T. Global daily sea surface temperature analysis using data from satellite microwave radiometer, satellite infrared radiometer and in-situ observations. Weath. Bull. 2006, 73, 1–18. (In Japanese) [Google Scholar]
- Donlon, C.J.; Martin, M.; Stark, J.D.; Robert-Jones, J.; Fiedler, E.; Wimmer, W. The operational sea surface temperature and sea ice analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar]
- Gentemann, C.L.; Wentz, F.J.; DeMaria, M. Near real time global optimum interpolated microwave SSTs: Applications to hurricane intensity forecasting. In Proceedings of the 27th Conference on Hurricanes and Tropical Meteorology, Monterey, CA, USA, 23–28 April 2006. [Google Scholar]
- Gentemann, C.L.; Wentz, F.J.; Brewer, M.; Hilburn, K.; Smith, D. Passive Microwave Remote Sensing of the Ocean: An Overview. In Oceanography from Space; Barale, V., Gower, J.F.R., Alberotanza, L., Eds.; Springer: The Hague, The Netherlands, 2010; pp. 13–33. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap. In Monographs on Statistics and Applied Probability; Chapman & Hall/CRC: New York, NY, USA, 1993; pp. 1–436. [Google Scholar]
- Lorenc, A.C.; Bell, R.S.; Macpherson, B. The Meteorological Office analysis correction data assimilation scheme. Quart. J. R. Meteor. Soc. 1991, 117, 59–89. [Google Scholar] [CrossRef]
- Martin, M.J.; Hines, A.; Bell, M.J. Data assimilation in the FOAM operational short-range ocean forecasting system: A description of the scheme and its impact. Quart. J. R. Meteor. Soc. 2007, 133, 981–995. [Google Scholar] [CrossRef]
- Bell, M.J.; Forbes, R.M.; Hines, A. Assessment of the FOAM global data assimilation system for real-time operational ocean forecasting. J. Mar. Syst. 2000, 25, 1–22. [Google Scholar] [CrossRef]
- Bell, M.; Barciela, R.; Hines, A.; Martin, M.; McCulloch, M.; Storkey, D. The forecasting ocean assimilation model (FOAM) system. In Building the European Capacity in Operational Oceanography; Dahlin, H., Flemming, N.C., Nittis, K., Petersson, S.E., Eds.; Elsevier: Athens, Greece, 2003; pp. 197–202. [Google Scholar]
- Bell, M.J.; Barciela, R.; Hines, A.; Martin, M.; Sellar, A.; Storkey, D. The Forecasting Ocean Assimilation Model (Foam) System. In Ocean Weather Forecasting; Chassignet, E.P., Verron, J., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 397–411. [Google Scholar]
- Tokinaga, H.; Xie, S.-P. Ocean tidal cooling effect on summer sea fog over the Okhotsk Sea. J. Geophys. Res. 2009, 114, D14102. [Google Scholar] [CrossRef] [Green Version]
- Heo, K.; Ha, K. A coupled model study on the formation and dissipation of sea fogs. Mon. Weather Rev. 2010, 138, 1186–1205. [Google Scholar] [CrossRef]
- Zhang, S.-P.; Xie, S.-P.; Liu, Q.-Y.; Yang, Y.-Q.; Wang, X.-G.; Ren, Z.-P. Seasonal variations of Yellow Sea fog: Observations and mechanisms. J. Clim. 2009, 22, 6758–6772. [Google Scholar]
- Kilpatrick, K.A.; Podesta, G.P.; Evans, R. Overview of the NOAA/NASA advanced very high resolution radiometer Pathfinder algorithm for sea surface temperature and associated matchup database. J. Geophys. Res. 2001, 106, 9179–9198. [Google Scholar] [CrossRef]



















| Product | Grid Spacing & SST Type | Institution and Country | Reference |
|---|---|---|---|
| OISST | 0.25° 0.5-m bulk | NCDC/NOAA, USA | Reynolds et al. [27] |
| MGDSST | 0.25° Foundation | Japan Meteorological Agency, Japan | Kurihara et al. [28] |
| OSTIA | 0.05° Foundation | Met Office, UK | Donlon et al. [29] |
| MWIR | 9 km Foundation | Remote Sensing Systems, USA | Gentemann et al. [30] |
| GMPE | 0.25° Ensemble | Met Office, UK | Martin et al. [6] |
| Product | Argo Floats | Buoys GTS | Ships GTS | AVHRR NOAA | AVHRR MetOP | MODIS Aqua,Terra | SEVIRI MSG | TMI TRMM | WindSat |
|---|---|---|---|---|---|---|---|---|---|
| OISST | ● | ● | |||||||
| MGDSST | ● | ● | ● | ● | ● | ||||
| OSTIA | ● | ● | ● | ● | ● | ● | |||
| MWIR | ● | ● | ● |
| Location | OISST | MGDSST | OSTIA | MWIR | GMPE | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSD | Bias | RMSD | Bias | RMSD | Bias | RMSD | Bias | RMSD | Bias | |
| KB (1399) | 1.00 0.04 | −0.08 0.05 | 0.79 0.03 | −0.20 0.04 | 0.77 0.03 | −0.11 0.04 | 0.83 0.03 | 0.17 0.04 | 0.68 0.03 | −0.12 0.04 |
| SB (632) | 1.13 0.06 | −0.04 0.09 | 0.95 0.05 | 0.20 0.07 | 0.82 0.04 | −0.14 0.06 | 0.87 0.04 | 0.17 0.07 | 0.87 0.05 | 0.11 0.07 |
| D (1240) | 1.97 0.07 | 1.37 0.08 | 1.46 0.05 | 1.02 0.06 | 0.88 0.04 | 0.41 0.04 | 2.22 0.09 | 1.41 0.10 | 1.54 0.06 | 1.07 0.06 |
| O (1283) | 1.04 0.04 | 0.36 0.05 | 0.78 0.03 | 0.39 0.06 | 0.45 0.02 | 0.04 0.02 | 0.98 0.04 | 0.50 0.05 | 0.76 0.03 | 0.38 0.04 |
| NIFS (1246) | 1.26 0.05 | 0.27 0.07 | 1.02 0.04 | 0.06 0.06 | 0.96 0.04 | 0.13 0.05 | 1.39 0.06 | 0.45 0.07 | 1.04 0.05 | 0.25 0.06 |
| Mean | 1.17 | 0.38 | 0.95 | 0.29 | 0.88 | 0.12 | 1.12 | 0.54 | 0.91 | 0.34 |
| Mixedregion | March–May | June–August | September–November | December–February | ||||
|---|---|---|---|---|---|---|---|---|
| Buoy | CTD | Buoy | CTD | Buoy | CTD | Buoy | CTD | |
| OISST | 1.50 0.07 | 1.50 0.16 | 2.09 0.11 | 2.43 0.30 | 0.79 0.04 | 0.86 0.12 | 0.95 0.04 | 1.20 0.14 |
| MGDSST | 0.70 0.04 | 0.85 0.12 | 1.55 0.08 | 2.19 0.26 | 0.90 0.05 | 0.79 0.11 | 0.92 0.05 | 0.86 0.10 |
| OSTIA | 0.59 0.03 | 0.94 0.14 | 0.93 0.06 | 1.82 0.21 | 0.49 0.03 | 0.72 0.09 | 0.45 0.02 | 1.06 0.12 |
| MWIR | 1.07 0.05 | 0.86 0.12 | 2.26 0.14 | 2.85 0.35 | 1.02 0.06 | 1.49 0.23 | 1.43 0.07 | 1.68 0.19 |
| GMPE | 0.79 0.04 | 0.88 0.13 | 1.78 0.10 | 2.40 0.30 | 0.64 0.04 | 0.85 0.13 | 0.77 0.04 | 0.95 0.12 |
| Mean | 0.93 | 1.01 | 1.72 | 2.34 | 0.77 | 0.94 | 0.90 | 1.15 |
| Stratifiedregion | March–May | June–August | September–November | December–February | ||||
|---|---|---|---|---|---|---|---|---|
| Buoy | CTD | Buoy | CTD | Buoy | CTD | Buoy | CTD | |
| OISST | 1.04 0.05 | 1.16 0.11 | 1.45 0.09 | 1.14 0.09 | 0.80 0.05 | 0.50 0.06 | 0.60 0.03 | 0.71 0.06 |
| MGDSST | 0.82 0.04 | 0.70 0.07 | 1.13 0.06 | 1.11 0.10 | 0.74 0.05 | 0.64 0.06 | 0.53 0.03 | 0.45 0.04 |
| OSTIA | 0.70 0.04 | 0.50 0.05 | 0.94 0.05 | 0.95 0.08 | 0.66 0.04 | 0.54 0.06 | 0.70 0.04 | 0.58 0.05 |
| MWIR | 0.89 0.04 | 0.81 0.07 | 0.85 0.05 | 0.84 0.07 | 0.74 0.05 | 0.57 0.07 | 0.93 0.05 | 0.73 0.06 |
| GMPE | 0.59 0.04 | 0.45 0.05 | 0.98 0.07 | 0.80 0.09 | 0.67 0.04 | 0.65 0.08 | 0.37 0.02 | 0.45 0.04 |
| Mean | 0.81 | 0.72 | 1.07 | 0.97 | 0.72 | 0.58 | 0.63 | 0.58 |
| Quality Flag | Best | Acceptable | Low | Bad | Worst | Total Number |
|---|---|---|---|---|---|---|
| Sea fog formation | 0 | 0 | 31 | 14 | 77 | 122 |
| No sea fog | 17 | 12 | 17 | 8 | 269 | 323 |
| Total number | 17 | 12 | 48 | 22 | 346 | 445 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, K.; Choi, B.-J.; Kim, S.-D.; Lee, S.-H.; Park, K.-A. Assessment and Improvement of Global Gridded Sea Surface Temperature Datasets in the Yellow Sea Using In Situ Ocean Buoy and Research Vessel Observations. Remote Sens. 2020, 12, 759. https://doi.org/10.3390/rs12050759
Kwon K, Choi B-J, Kim S-D, Lee S-H, Park K-A. Assessment and Improvement of Global Gridded Sea Surface Temperature Datasets in the Yellow Sea Using In Situ Ocean Buoy and Research Vessel Observations. Remote Sensing. 2020; 12(5):759. https://doi.org/10.3390/rs12050759
Chicago/Turabian StyleKwon, Kyungman, Byoung-Ju Choi, Sung-Dae Kim, Sang-Ho Lee, and Kyung-Ae Park. 2020. "Assessment and Improvement of Global Gridded Sea Surface Temperature Datasets in the Yellow Sea Using In Situ Ocean Buoy and Research Vessel Observations" Remote Sensing 12, no. 5: 759. https://doi.org/10.3390/rs12050759
APA StyleKwon, K., Choi, B. -J., Kim, S. -D., Lee, S. -H., & Park, K. -A. (2020). Assessment and Improvement of Global Gridded Sea Surface Temperature Datasets in the Yellow Sea Using In Situ Ocean Buoy and Research Vessel Observations. Remote Sensing, 12(5), 759. https://doi.org/10.3390/rs12050759