Evaluation and Comparison of Light Use Efficiency and Gross Primary Productivity Using Three Different Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.1.1. Data from FLUXNET
2.1.2. MODIS Data Processing
2.1.3. GLASS Data
2.1.4. ERA-Interim Data
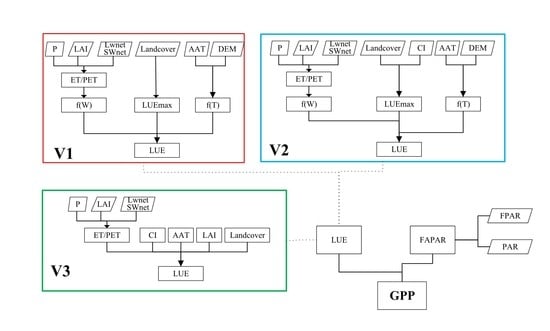
2.2. Methods
2.2.1. LUE Estimation
2.2.2. GPP Estimation
2.2.3. Calibration and Validation
3. Results
3.1. Validation of Global LUE and GPP Results in 2014
3.2. LUE
3.2.1. Parameterization Approach without the CI
3.2.2. Parameterization Approach with CI
3.2.3. Cubist Regression Tree Approach
3.3. GPP
4. Discussion
4.1. Comparison of Three Approaches
4.1.1. Comparison between the Parameterization Approach with and without the CI
4.1.2. Comparison between Parameterization Approaches and Regression Tree Approach
4.2. Uncertainty Analysis
4.3. Error Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Running, S.W.; Baldocchi, D.; Turner, D.; Gower, S.T.; Bakwin, P.; Hibbard, K. A global terrestrial monitoring network integrating tower fluxes, flask sampling, ecosystem modeling and EOS satellite data. Remote Sens. Environ. 1999, 70, 108–127. [Google Scholar] [CrossRef]
- Tramontana, G.; Ichii, K.; Camps-Valls, G.; Tomelleri, E.; Papale, D. Uncertainty analysis of gross primary production upscaling using Random Forests, remote sensing and eddy covariance data. Remote Sen. Environ. 2015, 168, 360–373. [Google Scholar] [CrossRef]
- McCallum, I.; Franklin, O.; Moltchanova, E.V.; Merbold, L.; Schmullius, C.; Shvidenko, A.; Schepaschenko, D.; Fritz, S. Improved light and temperature responses for light-use-efficiency-based GPP models. Biogeosciences 2013, 10, 6577–6590. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Chen, J.M.; Liu, J.; Bélair, S.; Luo, X. Assessment of SMAP soil moisture for global simulation of gross primary production. J. Geophys. Res. 2017, 122, 1549–1563. [Google Scholar] [CrossRef]
- Fletcher, B.J.; Gornall, J.L.; Poyatos, R.; Press, M.C.; Stoy, P.C.; Huntley, B.; Baxter, R.; Phoenix, G.K. Photosynthesis and productivity in heterogeneous arctic tundra: Consequences for ecosystem function of mixing vegetation types at stand edges. J. Ecol. 2012, 100, 441–451. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Guan, L.; Liu, X. Directly estimating diurnal changes in GPP for C3 and C4 crops using far-red sun-induced chlorophyll fluorescence. Agric. For. Meteorol. 2017, 232, 1–9. [Google Scholar]
- Missik, J.; Benson, M.C.; Oishi, A.C.; Novick, K.A.; Miniat, C. Quantifying Age-Related Hydraulic and Biochemical Constraints on Tree Photosynthesis in the Southern Appalachian Mountains. In Proceedings of the Agu Fall Meeting, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Wang, S.; Ibrom, A.; Bauer-Gottwein, P.; Garcia, M. Incorporating diffuse radiation into a light use efficiency and evapotranspiration model: An 11-year study in a high latitude deciduous forest. Agric. For. Meteorol. 2018, 248, 479–493. [Google Scholar] [CrossRef] [Green Version]
- Cramer, W.; Kicklighter, D.W.; Bondeau, A.; Iii, B.M.; Churkina, G.; Nemry, B.; Ruimy, A.; Schloss, A.L.; Intercomparison, T.P. Comparing global models of terrestrial net primary productivity (NPP): Overview and key results. Glob. Chang. Biol. 1999, 5, 1–15. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Sun, G.; Band, L.E.; McNulty, S.; Noormets, A.; Zhang, Q.; Zhang, Z. Development of a coupled carbon and water model for estimating global gross primary productivity and evapotranspiration based on eddy flux and remote sensing data. Agric. For. Meteorol. 2016, 223, 116–131. [Google Scholar] [CrossRef] [Green Version]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Christian, B.; Markus, R.; Enrico, T.; Philippe, C.; Martin, J.; Nuno, C.; Christian, R.D.; M Altaf, A.; Dennis, B.; Bonan, G.B. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar]
- Dan, L.; Wenwen, C.; Jiangzhou, X.; Wenjie, D.; Guangsheng, Z.; Yang, C.; Haicheng, Z.; Wenping, Y. Global validation of a process-based model on vegetation gross primary production using eddy covariance observations. PLoS ONE 2014, 9, e110407. [Google Scholar]
- Anav, A.; Friedlingstein, P.; Beer, C.; Ciais, P.; Harper, A.; Jones, C.; Murray-Tortarolo, G.; Papale, D.; Parazoo, N.C.; Peylin, P. Spatio-temporal patterns of terrestrial gross primary production: A review. Rev. Geophys. 2015, 53, 785–818. [Google Scholar] [CrossRef] [Green Version]
- Maosheng, Z.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940. [Google Scholar]
- Pan, S.; Tian, H.; Dangal, S.R.S.; Ouyang, Z.; Chaoqun, L.U.; Yang, J.; Tao, B. Impacts of climate variability and extremes on global net primary production in the first decade of the 21st century. J. Geogr. Sci. 2015, 25, 1027–1044. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore III, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Wu, C.; Chen, J.M.; Huang, N. Predicting gross primary production from the enhanced vegetation index and photosynthetically active radiation: Evaluation and calibration. Remote Sens. Environ. 2011, 115, 3424–3435. [Google Scholar] [CrossRef]
- Shi, H.; Li, L.; Eamus, D.; Huete, A.; Cleverly, J.; Tian, X.; Yu, Q.; Wang, S.; Montagnani, L.; Magliulo, V. Assessing the ability of MODIS EVI to estimate terrestrial ecosystem gross primary production of multiple land cover types. Ecol. Indic. 2017, 72, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1977, 281, 277–294. [Google Scholar]
- Monteith, J. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef] [Green Version]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global Terrestrial Gross and Net Primary Productivity from the Earth Observing System. In Methods in Ecosystem Science; Springer: Berlin/Heidelberg, Germany, 2000; pp. 44–57. [Google Scholar]
- Wu, C.Y.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Mäkelä, A.; Pulkkinen, M.; Kolari, P.; Lagergren, F.; Berbigier, P.; Lindroth, A.; Loustau, D.; Nikinmaa, E.; Vesala, T.; Hari, P. Developing an empirical model of stand GPP with the LUE approach: Analysis of eddy covariance data at five contrasting conifer sites in Europe. Glob. Chang. Biol. 2008, 14, 92–108. [Google Scholar] [CrossRef]
- McCallum, I.; Wagner, W.; Schmullius, C.; Shvidenko, A.; Obersteiner, M.; Fritz, S.; Nilsson, S. Satellite-based terrestrial production efficiency modeling. Carbon Balance Manag. 2009, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Jia, G.; Fu, C.; Feng, J.; Zhao, T.; Ma, Z. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ. 2010, 114, 2248–2258. [Google Scholar] [CrossRef]
- Norman, J.; Anderson, M.; Diak, G. An approach for mapping light-use efficiency on regional scales using satellite observations. In Proceedings of the 1996 International Geoscience and Remote Sensing Symposium, Lincoln, NE, USA, 27–31 May 1996; pp. 2358–2360. [Google Scholar]
- Gamon, J.A.; Bond, B. Effects of irradiance and photosynthetic downregulation on the photochemical reflectance index in Douglas-fir and ponderosa pine. Remote Sens. Environ. 2013, 135, 141–149. [Google Scholar] [CrossRef]
- Castro, S.; Sanchez-Azofeifa, A. Testing of Automated Photochemical Reflectance Index Sensors as Proxy Measurements of Light Use Efficiency in an Aspen Forest. Sensors 2018, 18, 3302. [Google Scholar] [CrossRef] [Green Version]
- Hmimina, G.; Merlier, E.; Dufrene, E.; Soudani, K. Deconvolution of pigment and physiologically related photochemical reflectance index variability at the canopy scale over an entire growing season. Plant Cell Environ. 2015, 38, 1578–1590. [Google Scholar] [CrossRef] [PubMed]
- Merlier, E.; Hmimina, G.; Dufrene, E.; Soudani, K. Explaining the variability of the photochemical reflectance index (PRI) at the canopy-scale: Disentangling the effects of phenological and physiological changes. J. Photochem. Photobiol. B-Biol. 2015, 151, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Ju, W.; Chen, J.; Wang, H.; Yang, F.; Fan, W.; Huang, Q.; Zheng, T.; Feng, Y.; Zhou, Y.; et al. Ability of the Photochemical Reflectance Index to Track Light Use Efficiency for a Sub-Tropical Planted Coniferous Forest. Remote Sens. 2015, 7, 16938–16962. [Google Scholar] [CrossRef] [Green Version]
- Porcar-Castell, A.; Garcia-Plazaola, J.I.; Nichol, C.J.; Kolari, P.; Olascoaga, B.; Kuusinen, N.; Fernandez-Marin, B.; Pulkkinen, M.; Juurola, E.; Nikinmaa, E. Physiology of the seasonal relationship between the photochemical reflectance index and photosynthetic light use efficiency. Oecologia 2012, 170, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Huete, A.; Yu, Q.; Restrepo-Coupe, N.; Beringer, J.; Hutley, L.B.; Kanniah, K.D.; Cleverly, J.; Eamus, D. Parameterization of an ecosystem light-use-efficiency model for predicting savanna GPP using MODIS EVI. Remote Sens. Environ. 2014, 154, 253–271. [Google Scholar] [CrossRef]
- Wei, S.; Yi, C.; Fang, W.; Hendrey, G. A global study of GPP focusing on light-use efficiency in a random forest regression model. Ecosphere 2017, 8, e01724. [Google Scholar] [CrossRef]
- Horn, J.E.; Schulz, K. Spatial extrapolation of light use efficiency model parameters to predict gross primary production. J. Adv. Model. Earth Syst. 2011, 3. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Song, C.H.; Sun, G.; Band, L.E.; Noormets, A.; Zhang, Q.F. Understanding moisture stress on light use efficiency across terrestrial ecosystems based on global flux and remote-sensing data. J. Geophys. Res. Biogeosci. 2015, 120, 2053–2066. [Google Scholar] [CrossRef]
- Xin, Q.C.; Gong, P.; Suyker, A.E.; Si, Y.L. Effects of the partitioning of diffuse and direct solar radiation on satellite-based modeling of crop gross primary production. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 51–63. [Google Scholar] [CrossRef]
- He, M.Z.; Ju, W.M.; Zhou, Y.L.; Chen, J.M.; He, H.L.; Wang, S.Q.; Wang, H.M.; Guan, D.X.; Yan, J.H.; Li, Y.N.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Xie, X.; Li, A.; Jin, H.; Yin, G.; Nan, X. Derivation of temporally continuous leaf maximum carboxylation rate (V-cmax) from the sunlit leaf gross photosynthesis productivity through combining BEPS model with light response curve at tower flux sites. Agric. For. Meteorol. 2018, 259, 82–94. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, J.M. Photochemical reflectance ratio for tracking light use efficiency for sunlit leaves in two forest types. Isprs J. Photogramm. Remote Sens. 2017, 123, 47–61. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Hilker, T.; Ju, W.M.; Coops, N.C.; Black, T.A.; Chen, J.M.; Wu, X.C. Modeling Gross Primary Production for Sunlit and Shaded Canopies Across an Evergreen and a Deciduous Site in Canada. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1859–1873. [Google Scholar] [CrossRef]
- Kumar, R.; Umanand, L. Estimation of global radiation using clearness index model for sizing photovoltaic system. Renew. Energy 2005, 30, 2221–2233. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Wei, H.; Li, C.; Qiao, Q.; Armaghani, D.J. Random forests and cubist algorithms for predicting shear strengths of rockfill materials. Appl. Sci. 2019, 9, 1621. [Google Scholar] [CrossRef] [Green Version]
- Noi, P.T.; Degener, J.; Kappas, M. Comparison of multiple linear regression, cubist regression, and random forest algorithms to estimate daily air surface temperature from dynamic combinations of MODIS LST data. Remote Sens. 2017, 9, 398. [Google Scholar] [CrossRef] [Green Version]
- Houborg, R.; McCabe, M.F. A hybrid training approach for leaf area index estimation via Cubist and random forests machine-learning. ISPRS J. Photogramm. Remote Sens. 2018, 135, 173–188. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Schwalm, C.R.; Jassal, R.S.; Black, T.A.; Krishnan, P. Effects of mutual shading of tree crowns on prediction of photosynthetic light-use efficiency in a coastal Douglas-fir forest. Tree phys. 2008, 28, 825–834. [Google Scholar] [CrossRef]
- Schubert, P.; Lagergren, F.; Aurela, M.; Christensen, T.; Grelle, A.; Heliasz, M.; Klemedtsson, L.; Lindroth, A.; Pilegaard, K.; Vesala, T.; et al. Modeling GPP in the Nordic forest landscape with MODIS time series data—Comparison with the MODIS GPP product. Remote Sens. Environ. 2012, 126, 136–147. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S. A continuous measure of gross primary production for the conterminous United States derived from MODIS and AmeriFlux data. Remote Sens. Environ. 2010, 114, 576–591. [Google Scholar] [CrossRef] [Green Version]
- Boyte, S.P.; Wylie, B.K.; Howard, D.M.; Dahal, D.; Gilmanov, T. Estimating carbon and showing impacts of drought using satellite data in regression-tree models. Int. J. Remote Sens. 2017, 39, 374–398. [Google Scholar] [CrossRef]
- McCree, K.J. Test of current definitions of photosynthetically active radiation against leaf photosynthesis data. Agric. Meteorol. 1972, 10, 443–453. [Google Scholar] [CrossRef]
- Vermote, E.F.; El Saleous, N.; Justice, C.O.; Kaufman, Y.J.; Privette, J.L.; Remer, L.; Roger, J.C.; Tanré, D. Atmospheric correction of visible to middle-infrared EOS-MODIS data over land surfaces: Background, operational algorithm and validation. J. Geophys. Res. Atmos. 1997, 102, 17131–17141. [Google Scholar] [CrossRef] [Green Version]
- Vermote, E.F.; Saleous, E.L.; Nazmi, Z.; Christopher, O. Atmospheric correction of MODIS data in the visible to middle infrared: First results. Remote Sens. Environ. 2002, 83, 97–111. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M.; Shuey, C.J.; Walthall, C.; Daughtry, C.; Morisette, J.; Schaaf, C.; Strahler, A. Validating MODIS land surface reflectance and albedo products: Methods and preliminary results. Remote Sens. Environ. 2002, 83, 149–162. [Google Scholar] [CrossRef]
- Chen, J.M.; Feng, D.; Mingzhen, C. Locally adjusted cubic-spline capping for reconstructing seasonal trajectories of a satellite-derived surface parameter. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2230–2238. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Sun, R. Evaluation of Three Long Time Series for Global Fraction of Absorbed Photosynthetically Active Radiation (FAPAR) Products. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5509–5524. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.; Liu, Z.; Yang, B.; Chen, C.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 2: Validation and Intercomparison. Remote Sens. 2016, 8, 460. [Google Scholar] [CrossRef] [Green Version]
- Liang, S.; Zhang, X.; Xiao, Z.; Cheng, J.; Liu, Q.; Zhao, X. Global LAnd Surface Satellite (GLASS) Products: Algorithms, Validation and Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Muñoz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef] [Green Version]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Rui, S.; Xu, Z.; Lei, Z.; Liu, L.; Hao, L.; Jiang, G. A Study of Shelterbelt Transpiration and Cropland Evapotranspiration in an Irrigated Area in the Middle Reaches of the Heihe River in Northwestern China. IEEE Geosci. Remote Sens. Lett. 2015, 12, 369–373. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.J.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol. 2009, 379, 92–110. [Google Scholar] [CrossRef]
- Priestley, C.H.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar]
- Cui, T.; Wang, Y.; Sun, R.; Qiao, C.; Fan, W.; Jiang, G.; Hao, L.; Zhang, L. Estimating Vegetation Primary Production in the Heihe River Basin of China with Multi-Source and Multi-Scale Data. PLoS ONE 2016, 11, e0153971. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar]
- Jiang, Z.; Chen, Z.; Ren, J.; Huang, Q. Inversion of winter wheat leaf area index based on canopy reflectance model and HJ CCD image. In Proceedings of the Second International Conference on Agro-geoinformatics, Fairfax, VA, USA, 12–16 August 2013. [Google Scholar]
- Gupta, V.K. Optimal Use of the SCE-UA Global Optimization Method for Calibrating Watershed Models. J. Hydrol. 1994, 158, 265–284. [Google Scholar]
- Kan, G.; He, X.; Ding, L.; Li, J.; Liang, K.; Hong, Y. A heterogeneous computing accelerated SCE-UA global optimization method using OpenMP, OpenCL, CUDA, and OpenACC. Water Sci. Technol. 2017, 76, 1640–1651. [Google Scholar]
- Jeon, J.H.; Park, C.G.; Engel, B.A. Comparison of Performance between Genetic Algorithm and SCE-UA for Calibration of SCS-CN Surface Runoff Simulation. Water 2014, 6, 3433–3456. [Google Scholar] [CrossRef] [Green Version]
- Huijuna, X.U.; Chen, Y.; Zeng, B.; Jinxianga, H.E.; Liao, Z. Application of SCE-UA Algorithm to Parameter Optimization of Liuxihe Model. Trop. Geogr. 2012, 32, 32–37. [Google Scholar]
- Song, X.; Zhan, C.; Xia, J. Integration of a statistical emulator approach with the SCE-UA method for parameter optimization of a hydrological model. Sci. Bull. 2012, 57, 3397–3403. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M.; Johnson, K. Regression trees and rule-based models. In Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; pp. 173–220. [Google Scholar]
- Running, S.W.; Zhao, M. Daily GPP and annual NPP (MOD17A2/A3) products NASA Earth Observing System MODIS land algorithm. 2015. Available online: https://www.ntsg.umt.edu/files/modis/MOD17UsersGuide2015_v3.pdf (accessed on 15 March 2020).
- Hoffman, M.T.; Carrick, P.; Gillson, L.; West, A. Drought, climate change and vegetation response in the succulent karoo, South Africa. S. Afr. J. Sci. 2009, 105, 54–60. [Google Scholar] [CrossRef]
- Carrao, H.; Naumann, G.; Barbosa, P. Mapping global patterns of drought risk: An empirical framework based on sub-national estimates of hazard, exposure and vulnerability. Glob. Environ. Chang. 2016, 39, 108–124. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hutley, L. Exploring the link between clouds, radiation, and canopy productivity of tropical savannas. Agric. Forest Meteorol. 2013, 182, 304–313. [Google Scholar] [CrossRef]














| IGBP Vegetation Type | Vegetation Type Abbreviation | |||
|---|---|---|---|---|
| Evergreen Needleleaf Forests | ENF | 1.432 | 0.573 | 2.556 |
| Evergreen Broadleaf Forests | EBF | 1.491 | 0.596 | 2.603 |
| Deciduous Needleleaf Forests | DNF | 0.831 | 0.332 | 1.400 |
| Deciduous Broadleaf Forests | DBF | 1.434 | 0.573 | 2.556 |
| Mixed Forests | MF | 1.540 | 0.616 | 2.494 |
| Closed Shrublands | CSH | 1.168 | 0.467 | 2.070 |
| Open Shrublands | OSH | 0.761 | 0.304 | 1.510 |
| Woody Savannas | WSA | 1.120 | 0.460 | 2.298 |
| Savannas | SAV | 1.301 | 0.520 | 2.466 |
| Grasslands | GRA | 1.277 | 0.511 | 2.398 |
| Croplands | CRO | 1.587 | 0.943 | 2.466 |
| Rule 1 | conditions | vegetation type in {CRO, DNF, WSA, OSH, GRA}, LAI ≤ 0.7 and EF ≤ 0.753 |
| linear formula | LUE = 0.047 + 0.159 LAI + 0.78 EF − 0.11 CI | |
| Rule 2 | conditions | vegetation type in {DBF, SAV} and Tmean ≤ 11.562 |
| linear formula | LUE = -0.042 + 0.13 LAI + 0.62 EF + 0.0119 Tmean − 0.07 CI | |
| Rule 3 | conditions | vegetation type = WSA |
| linear formula | LUE = 0.338 + 1 EF - 0.006 Tmean + 0.02 LAI | |
| Rule 4 | conditions | vegetation type in {CRO, DNF, OSH, GRA}, LAI > 0.7 and EF ≤ 0.753 |
| linear formula | LUE = 0.207 + 1.08 EF + 0.091 LAI − 0.006 Tmean − 0.4 CI | |
| Rule 5 | conditions | vegetation type in {MF, ENF, EBF, CSH} and Tmean ≤ 11.562 |
| linear formula | LUE = 0.784 + 0.029 Tmean + 0.68 EF − 1.12 CI + 0.062 LAI | |
| Rule 6 | conditions | vegetation type in {DBF, SAV, MF, ENF, EBF, CSH}, Tmean > 11.562 and EF ≤ 0.753 |
| linear formula | LUE = 0.682 + 1.17 EF − 0.57 CI - 0.0066 Tmean + 0.014 LAI | |
| Rule 7 | conditions | LAI ≤ 1.8 and EF > 0.753 |
| linear formula | LUE = -0.514 + 0.409 LAI + 1.47 EF + 0.025 Tmean − 1.05 CI | |
| Rule 8 | conditions | vegetation type in {DBF, WSA, SAV, MF, GRA, ENF, EBF, CSH}, LAI > 1.8 and EF > 0.7531864 |
| linear formula | LUE = 0.862 + 1.26 EF − 1.41 CI + 0.021 LAI | |
| Rule 9 | conditions | CI <= 0.447, LAI > 1.8 and EF > 0.753 |
| linear formula | LUE = 0.439 + 1.71 EF − 0.93 CI | |
| Rule 10 | conditions | vegetation type = CRO, LAI > 1.8 and EF > 0.753 |
| linear formula | LUE = −0.831 + 3.24 EF + 0.0316 Tmean − 1.53 CI |
| IGBP | V1 | V2 | V3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LUE | GPP | LUE | GPP | LUE | GPP | |||||||
| R2 | RMSE (gC/MJ) | R2 | RMSE (gC/m2/d) | R2 | RMSE (gC/MJ) | R2 | RMSE (gC/m2/d) | R2 | RMSE (gC/MJ) | R2 | RMSE (gC/m2/d) | |
| CRO | 0.02 | 0.58 | 0.46 | 2.74 | 0.03 | 0.57 | 0.46 | 2.73 | 0.01 | 0.88 | 0.22 | 4.42 |
| DBF | 0.43 | 0.42 | 0.64 | 3.14 | 0.45 | 0.41 | 0.65 | 3.06 | 0.11 | 0.73 | 0.40 | 3.74 |
| DNF | 0.43 | 0.24 | 0.80 | 1.70 | 0.48 | 0.24 | 0.74 | 1.76 | 0.48 | 0.20 | 0.61 | 1.24 |
| EBF | 0.00 | 0.46 | 0.53 | 3.18 | 0.01 | 0.43 | 0.50 | 3.03 | 0.26 | 0.37 | 0.48 | 3.18 |
| ENF | 0.13 | 0.46 | 0.49 | 2.65 | 0.17 | 0.46 | 0.50 | 2.61 | 0.09 | 0.62 | 0.51 | 2.80 |
| GRA | 0.26 | 0.42 | 0.56 | 2.45 | 0.34 | 0.41 | 0.61 | 2.27 | 0.22 | 0.49 | 0.52 | 2.58 |
| MF | 0.29 | 0.37 | 0.72 | 2.29 | 0.36 | 0.35 | 0.72 | 2.15 | 0.20 | 0.37 | 0.64 | 2.16 |
| OSH | 0.10 | 0.31 | 0.21 | 0.88 | 0.19 | 0.28 | 0.31 | 0.86 | 0.07 | 0.35 | 0.23 | 1.13 |
| SAV | 0.06 | 0.26 | 0.48 | 1.52 | 0.19 | 0.23 | 0.54 | 1.51 | 0.12 | 0.35 | 0.32 | 2.01 |
| WSA | 0.38 | 0.29 | 0.62 | 1.82 | 0.38 | 0.29 | 0.66 | 1.81 | 0.55 | 0.26 | 0.70 | 1.73 |
| Site ID | Site Name | Latitude (°) | Longitude (°) | Elevation (m) | Landcover | Mean Annual Temperature (°C) | Mean Annual Precipitation (mm) |
|---|---|---|---|---|---|---|---|
| IT-Isp | Ispra ABC-IS | 45.813 | 8.634 | 210 | DBF | 12.2 | 1300 |
| AU-Whr | Whroo | −36.673 | 145.029 | 152 | EBF | 16.7 | 625 |
| CH-Cha | Chamau | 47.210 | 8.410 | 393 | GRA | 9.5 | 1136 |
| SE-St1 | Stordalen grassland | 68.354 | 19.050 | 351 | WET | −0.7 | 303.3 |
| US-WCr | Willow Creek | 45.806 | −90.080 | 520 | DBF | 4.02 | 787 |
| US-Me2 | Metolius mature ponderosa pine | 44.452 | −121.557 | 1253 | ENF | 6.28 | 523 |
| AU-Gin | Gingin | −31.376 | 115.714 | 105 | WSA | 18.76 | 346 |
| DE-Kli | Klingenberg | 50.893 | 13.522 | 478 | CRO | 7.6 | 842 |
| CH-Oe2 | Oensingen crop | 47.286 | 7.734 | 452 | CRO | 9.8 | 1155 |
| US-Los | Lost Creek | 46.083 | −89.979 | 480 | WET | 4.08 | 828 |
| US-Tw4 | Twitchell East End Wetland | 38.103 | −121.641 | −5 | WET | 15.6 | 421 |
| CH-Lae | Laegern | 47.478 | 8.364 | 689 | MF | 8.3 | 1100 |
| US-SRG | Santa Rita Grassland | 31.789 | −110.828 | 1291 | GRA | 17 | 420 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Sun, R.; Zhu, A.; Xiao, Z. Evaluation and Comparison of Light Use Efficiency and Gross Primary Productivity Using Three Different Approaches. Remote Sens. 2020, 12, 1003. https://doi.org/10.3390/rs12061003
Wang M, Sun R, Zhu A, Xiao Z. Evaluation and Comparison of Light Use Efficiency and Gross Primary Productivity Using Three Different Approaches. Remote Sensing. 2020; 12(6):1003. https://doi.org/10.3390/rs12061003
Chicago/Turabian StyleWang, Mengjia, Rui Sun, Anran Zhu, and Zhiqiang Xiao. 2020. "Evaluation and Comparison of Light Use Efficiency and Gross Primary Productivity Using Three Different Approaches" Remote Sensing 12, no. 6: 1003. https://doi.org/10.3390/rs12061003
APA StyleWang, M., Sun, R., Zhu, A., & Xiao, Z. (2020). Evaluation and Comparison of Light Use Efficiency and Gross Primary Productivity Using Three Different Approaches. Remote Sensing, 12(6), 1003. https://doi.org/10.3390/rs12061003