Optical Water Type Guided Approach to Estimate Optical Water Quality Parameters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites and In Situ Dataset
2.1.1. Water-Leaving Reflectance (R(λ))
2.1.2. Analysis of Water Samples
2.2. Classification of Optical Water Types (OWTs)
2.3. Algorithms for Retrieving Water Quality Parameters
- RMSE (Root Mean Squared Error)—represents the average difference between the measured values and the values predicted by the model. This metric indicates the fit of the model to the data. The lower the RMSE, the better the model.
- RMSLE (Root Mean Squared Logarithmic Error)—represents the average difference between the log-transformed measured values and the log-transformed values predicted by the model. This metric does not penalize big differences when both the predicted and the measured values are big numbers. This is useful when the measurement values are in a wide range. The lower the RMSLE, the better the model.
- MAE (Mean Absolute Error)—represents the average absolute difference between the measured and predicted model values. This metric measures the model prediction error and is robust against the effect of outliers. The lower the MAE, the better the model.
- MAPE (Mean Absolute Percentage Error)—measures the average absolute percentage error from the measured value and the values predicted by the model divided by the measured value. This metrics shows the model prediction accuracy. The lower the MAPE, the better the model.
- R2—represents the squared correlation between the measured values and the predicted values by the model. This metric shows the percentage of variance explained by the model. The closer to 1 the R2, the better the model.
- BIAS—represents the average amount by which the measured value is greater than predicted. The lower the bias, the better the model.
- p-value—tests the null hypothesis and shows if the model is statistically significant or not. A low p-value (<0.05) suggests that the model is statistically significant.
2.4. Satellite Dataset
3. Results
3.1. Description of In Situ Dataset
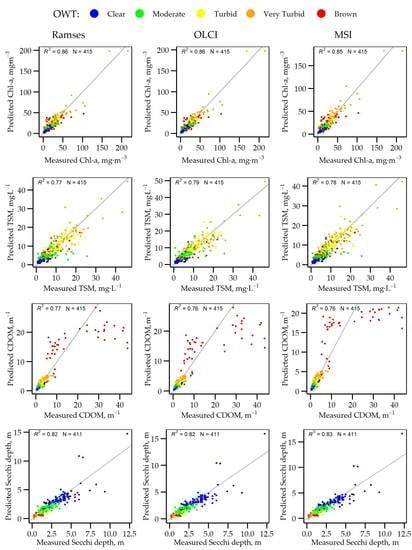
3.2. Predictive Models for Concentration of Chlorophyll-a (Chl-a)
| OWT | Model | Model Formula | ST 1 | R2 | p-value |
|---|---|---|---|---|---|
| Ramses | |||||
| Clear | CHL69 | LR | 0.79 | < 2.2E-16 | |
| Moderate | CHL97 | LR | 0.62 | < 2.2E-16 | |
| Turbid | CHL88 | LR | 0.79 | < 2.2E-16 | |
| Very Turbid | CHL97 | LR | 0.88 | < 2.2E-16 | |
| Brown | CHL67 | LR | 0.41 | 4.3E-06 | |
| OLCI | |||||
| Clear | CHL69 | LR | 0.78 | < 2.2E-16 | |
| Moderate | CHL65 | LR | 0.67 | < 2.2E-16 | |
| Turbid | CHL98 | LR | 0.79 | < 2.2E-16 | |
| Very Turbid | CHL97 | LR | 0.89 | < 2.2E-16 | |
| Brown | CHL67 | LR | 0.38 | 5.9E-06 | |
| MSI | |||||
| Clear | CHL101 | LR | 0.61 | < 2.2E-16 | |
| Moderate | CHL65 | LR | 0.60 | < 2.2E-16 | |
| Turbid | CHL57 | LR | 0.63 | < 2.2E-16 | |
| Very Turbid | CHL65 | LR | 0.89 | < 2.2E-16 | |
| Brown | CHL67 | LR | 0.40 | 6.0E-06 |
3.3. Predictive Models for Concentration of Total Suspended Matter (TSM)
| OWT | Model | Model Formula | ST 1 | R2 | p-value |
|---|---|---|---|---|---|
| Ramses | |||||
| Clear | TSM39 | LT-MLR | 0.47 | 5.7E-13 | |
| Moderate | TSM38 | LT-MLR | 0.36 | 1.5E-11 | |
| Turbid | TSM20 | LLR | 0.69 | < 2.2E-16 | |
| Very Turbid | TSM18 | LR | 0.68 | 9.8E-14 | |
| Brown | TSM18 | LR | 0.61 | 8.4E-10 | |
| OLCI | |||||
| Clear | TSM39 | LT-MLR | 0.47 | 3.5E-13 | |
| Moderate | TSM18 | LR | 0.45 | < 2.2E-16 | |
| Turbid | TSM18 | LR | 0.69 | < 2.2E-16 | |
| Very Turbid | TSM38 | LLR | 0.60 | 4.0E-09 | |
| Brown | TSM31 | LT-LR | 0.49 | 2.0E-07 | |
| MSI | |||||
| Clear | TSM39 | LT-MLR | 0.49 | 4.0E-14 | |
| Moderate | TSM38 | LT-MLR | 0.36 | 3.4E-10 | |
| Turbid | TSM18 | LR | 0.64 | < 2.2E-16 | |
| Very Turbid | TSM18 | LR | 0.68 | < 2.2E-16 | |
| Brown | TSM18 | LR | 0.54 | 1.8E-08 |
3.4. Predictive Models for Absorption Coefficient of Coloured Dissolved Organic Matter (CDOM)
| OWT | Model | Model Formula | ST 1 | R2 | p-value |
|---|---|---|---|---|---|
| Ramses | |||||
| Clear | CDOM131 | LLR | 0.74 | < 2.2E-16 | |
| Moderate | CDOM124 | LLR | 0.36 | 1.4E-13 | |
| Turbid | CDOM124 | LLR | 0.45 | 4.2E-14 | |
| Very Turbid | CDOM119 | LR | 0.42 | 2.3E-07 | |
| Brown | CDOM117 | LT-MLR | 0.38 | 8.1E-05 | |
| OLCI | |||||
| Clear | CDOM122 | LLR | 0.74 | < 2.2E-16 | |
| Moderate | CDOM122 | LLR | 0.33 | 7.1E-12 | |
| Turbid | CDOM122 | LLR | 0.32 | 6.8E-10 | |
| Very Turbid | CDOM119 | LR | 0.38 | 2.3E-06 | |
| Brown | CDOM117 | LT-MLR | 0.41 | 1.6E-05 | |
| MSI | |||||
| Clear | CDOM122 | LLR | 0.74 | < 2.2E-16 | |
| Moderate | CDOM122 | LLR | 0.42 | 1.6E-14 | |
| Turbid | CDOM122 | LLR | 0.31 | 1.9E-09 | |
| Very Turbid | CDOM119 | LR | 0.39 | 8.7E-08 | |
| Brown | CDOM133 | LT-MLR | 0.41 | 2.2E-05 |
3.5. Predictive Models for Secchi Disk Depth
| OWT | Model | Model Formula | ST 1 | R2 | p-value |
|---|---|---|---|---|---|
| Ramses | |||||
| Clear | ZSD104 | LT-MLR | 0.60 | < 2.2E-16 | |
| Moderate | ZSD104 | LT-MLR | 0.64 | < 2.2E-16 | |
| Turbid | ZSD104 | LT-MLR | 0.74 | < 2.2E-16 | |
| Very Turbid | ZSD112 | MLR | 0.48 | 9.6E-07 | |
| Brown | ZSD109 | LLR | 0.27 | 0.0005 | |
| OLCI | |||||
| Clear | ZSD104 | LT-MLR | 0.62 | < 2.2E-16 | |
| Moderate | ZSD104 | LT-MLR | 0.65 | < 2.2E-16 | |
| Turbid | ZSD104 | LT-MLR | 0.69 | < 2.2E-16 | |
| Very Turbid | ZSD112 | MLR | 0.48 | 1.6E-06 | |
| Brown | ZSD109 | LLR | 0.28 | 0.0003 | |
| MSI | |||||
| Clear | ZSD104 | LT-MLR | 0.64 | < 2.2E-16 | |
| Moderate | ZSD104 | LT-MLR | 0.68 | < 2.2E-16 | |
| Turbid | ZSD104 | LT-MLR | 0.63 | < 2.2E-16 | |
| Very Turbid | ZSD112 | MLR | 0.51 | 9.7E-09 | |
| Brown | ZSD109 | LLR | 0.29 | 0.0002 |
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Algorithm | Stat. Tech. | Sensor | Data Range | Waterbody | Country | Reference | |
|---|---|---|---|---|---|---|---|---|
| TSM1 | R858 | P2R | MODIS | 0.3–145.6 | Bay of Biscay | France | Petus et al. (2010) | [105] |
| TSM2 | R858/R645 | LR | MODIS | 77–2182 | Gironde Estuary | France | Chavula et al. (2009) | [106] |
| TSM3 | R645 | LR | MODIS | 1–55 | Gulf of Mexico | USA | Miller, McKee (2004) | [107] |
| TSM4 | R850/R550 | P3R | Radiometric | 13–985 | Gironde Estuary | France | Doxaran et al. (2002) | [108] |
| TSM5 | (R485-R830)/(R660-R830) | LT-LR | LS TM | 0.7–23 | Southern Finland lakes | Finland | Härmä et al. (2001) | [109] |
| TSM6 | R702 | LR | AISA | 0.7–32 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| TSM7 | R709.5) | LR | AISA | 0.7–32 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| TSM8 | R551 | LR | MODIS | 1.2–110.3 | Southern North Sea | Nechad et al. (2010) | [111] | |
| TSM9 | R850/R550 | LR | Radiometric | 13–985 | Gironde Estuary | France | Doxaran et al. (2002) | [108] |
| TSM10 | R702-R751 | LR | AISA | 0.7–32 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| TSM11 | (R560-R520)/(R560+R520) | LLR | Radiometric | 1–66 | Hungarian, Bulgarian, Germany lakes | Gitelson et al. (1993) | [112] | |
| TSM12 | R709-R779 | LR | MERIS | 0.7–23 | Finnish lakes | Finland | Härmä et al. (2001) | [109] |
| TSM13 | R490/R645 | LLR | Radiometric | Baltic Sea - southern | Poland | Woźniak (2014) | [113] | |
| TSM14 | R555/R645 | LLR | Radiometric | Baltic Sea - southern | Poland | Woźniak (2014) | [113] | |
| TSM15 | (R545+R645)/2 | LLR | SPOT, LS TM | Frisian lakes | Netherlands | Dekker et al. (2002) | [114] | |
| TSM16 | (R545+R645)/2 | LR | SPOT, LS TM | Frisian lakes | Netherlands | Dekker et al. (2002) | [114] | |
| TSM17 | max(R700–R720)-(R646+R770)/2 | LR | Radiometric | 0.75–63.33 | Estonian lakes | Estonia | Kutser et al. (2016) | [65] |
| TSM18 | R810-(R770+R840)/2 | LR | Radiometric | 0.75–63.33 | Estonian lakes | Estonia | Kutser et al. (2016) | [65] |
| TSM19 | R635 | LR | SEVIRI | 2–100 | North Sea – Belgian coast | Belgium | Neukermans et al. (2009) | [115] |
| TSM20 | R620·R681/R510 | LLR | New Caledonia lagoon, Cienfuegos Bay, Suva Harbour and Laucala Bay | New Caledonia, Cuba, Fiji | Ouillon et al. (2008) | [116] | ||
| TSM21 | R620·R681/R412 | LLR | New Caledonia lagoon, Cienfuegos Bay, Suva Harbour and Laucala Bay | New Caledonia, Cuba, Fiji | Ouillon et al. (2008) | [116] | ||
| TSM22 | R681 | P2R | New Caledonia lagoon, Cienfuegos Bay, Suva Harbour and Laucala Bay | New Caledonia, Cuba, Fiji | Ouillon et al. (2008) | [116] | ||
| TSM23 | R443/R670 | LLR | New Caledonia lagoon, Cienfuegos Bay, Suva Harbour and Laucala Bay | New Caledonia, Cuba, Fiji | Ouillon et al. (2008) | [116] | ||
| TSM24 | R560, R660, R830 | MLR | LS TM | 11.5–33.5 | Lake Reelfoot | USA | Wang et al. (2006) | [74] |
| TSM25 | R709/R754 | LT-LR | OLCI | 1.2–9.14 | Baltic Sea | Estonia | Toming et al. (2017) | [30] |
| TSM26 | R745/R490 | LT-LR | GOCI | 8–5275 | Lake Taihu | China | He et al. (2019) | [117] |
| TSM27 | R560 | LR | MSI | 5–38.76 | Gorky Reservoir | Russia | Molkov et al. (2019) | [118] |
| TSM28 | R560 | P2RR | MSI | 5–38.76 | Gorky Reservoir | Russia | Molkov et al. (2019) | [118] |
| TSM29 | R740 | P2R | MSI | 5–38.76 | Gorky Reservoir | Russia | Molkov et al. (2019) | [118] |
| TSM30 | R740/R705 | P2R | MSI | 5–38.76 | Gorky Reservoir | Russia | Molkov et al. (2019) | [118] |
| TSM31 | R705-(R740+R665)/2 | LT-LR | MSI | 5–38.76 | Gorky Reservoir | Russia | Molkov et al. (2019) | [118] |
| TSM32 | R908 | LR | WV 2 | >820 | inland waters in Deqing County | China | Shi et al. (2018) | [119] |
| TSM33 | R427 | LR | WV 2 | >820 | inland waters in Deqing County | China | Shi et al. (2018) | [119] |
| TSM34 | R658 | LR | WV 2 | >820 | inland waters in Deqing County | China | Shi et al. (2018) | [119] |
| TSM35 | R840/R545 | LT-LR | SPOT | 35–2000 | Gironde estuary | France | Doxaran et al. (2002) | [108] |
| TSM36 | R840/R645 | LT-LR | SPOT | 35–2000 | Gironde estuary | France | Doxaran et al. (2002) | [108] |
| TSM37 | (R550+R670)/(R550/R670) | LT10-LR | Han et al. (2006) | [120] | ||||
| TSM38 | log(R555), R645, log(R488/R555) | LT10-MLR | Gulf of Naples | Italy | Tassan (1993) | [121] | ||
| TSM39 | R555, R645, R488/R555 | LT10-MLR | Yellow Sea | China | Zhang et al. (2010) | [66] | ||
| CHL40 | R443/R551 | LR | MODIS | 0.1–0.4 | Lake Malawi | Malawi | Chavula et al. (2009) | [106] |
| CHL41 | R688/R674 | LR | AISA | 1.0–100 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| CHL42 | (1/R665-1/R708)/R753 | LR | MERIS | 0.63–65.51 | Taganrog Bay, Azov Sea | Russia | Moses et al. (2009) | [122] |
| CHL43 | R705/R664 | LR | CASI | 2.5–18.9 | Lake Märalen | Sweden | Ammenberg et al. (2002) | [68] |
| CHL44 | R550 | LR | CASI | 2.9–50.6 | Lakes Erken and Mälaren | Sweden | Flink et al. (2001) | [87] |
| CHL45 | R708/R678 | LR | CASI | 2.9–50.6 | Lakes Erken and Mälaren | Sweden | Flink et al. (2001) | [87] |
| CHL46 | R708/R678, R643/R628 | MLR | CASI | 2.9–50.6 | Lakes Erken and Mälaren | Sweden | Flink et al. (2001) | [87] |
| CHL47 | R700/R670 | LLR | Radiometric | 6.3–58.2 | Lake Chagan | China | Duan et al. (2007) | [88] |
| CHL48 | R560/R660 | LLR | LS TM | ∼5–50 | New York Harbour | USA | Hellweger et al. (2004) | [71] |
| CHL49 | (R485-R660)/R560 | LR | LS TM | 3.0–6.0 | Lake Garda | Italy | Brivio et al. (2001) | [123] |
| CHL50 | ln(R485), ln(R560) | LT-MLR | LS TM | 3.0–6.0 | Lake Garda | Italy | Brivio et al. (2001) | [123] |
| CHL51 | R485/R560 | LLR | LS TM | Arabian Sea | Dwivedi, Narain (1987) | [124] | ||
| CHL52 | R660/R485 | LLR | LS TM | 2.0–70.0 | Haifa Bay | Israel | Gitelson et al. (1996) | [125] |
| CHL53 | max(R400–R900)/R670 | LR | Radiometric | 5.1–185 | Lake Kinneret | Israel | Yacobi et al. (1995) | [126] |
| CHL54 | R830/R660 | LR | LS TM | 5.1–185 | Lake Kinneret | Israel | Yacobi et al. (1995) | [126] |
| CHL55 | R560 | LLR | LS TM | 1.0–50.3 | Lake Michigan | USA | Lathrop, Lillesand(1986) | [127] |
| CHL56 | R710/R670 | LT-LR | CASI-2 | ∼4–63 | Barton Broad | UK | Hunter et al. (2008) | [128] |
| CHL57 | (1/R650-1/R710)·R740 | LR | Radiometric | 107–3078 | Tamar Estuary | UK | Zimba, Gitelson (2006) | [11] |
| CHL58 | R704/R672 | LR | Radiometric | 3–185 | Inland waters | Neatherlands | Gons (1999) | [90] |
| CHL59 | sum(R670–R850) | LR | 21.0–280 | Carter Lake | USA | Schalles et al. (1998) | [129] | |
| CHL60 | sum(R670–R730) | LR | Radiometric | 3.1–7.3 | Lake Kinneret | Israel | Gitelson et al. (1994) | [130] |
| CHL61 | R700/R680 | LR | AMMS | 2–79 | Tennessee Vally | USA | Dierberg, Carriker (1994) | [89] |
| CHL62 | R688/R681 | LR | AISA | 1.0–100 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| CHL63 | R702/R664 | LR | AISA | 22–130 | Gulf of Finland | Finland | Koponen et al. (2007) | [91] |
| CHL64 | R665/R754 | LR | OLCI | 0–6.02 | Baltic Sea | Toming et al. (2017) | [30] | |
| CHL65 | R674/R709 | LR | OLCI | 0–6.02 | Baltic Sea | Toming et al. (2017) | [30] | |
| CHL66 | R674/R754 | LR | OLCI | 0–6.02 | Baltic Sea | Toming et al. (2017) | [30] | |
| CHL67 | R748/R667 | LR | MODIS | Dnieper River, Sea of Azov | Russia | Moses et al. (2009) | [92] | |
| CHL68 | (R490-R665)/R560 | LR | LS TM | 3-7 | Lake Kinneret | Israel | Mayo et al. (1995) | [131] |
| CHL69 | R709-(R665+R754)/2 | LR | Gitelson et al. (1992) | [60] | ||||
| CHL70 | R709-R754 | LR | Gitelson et al. (1992) | [60] | ||||
| CHL71 | R705-(R665+R740)/2 | LR | MSI | 3.6–72.9 | Estonian lakes | Estonia | Toming et al. (2016) | [27] |
| CHL72 | R709/R681 | LR | OLCI | 5.99–117.54 | Manguaba | Brazil | Lins et al. (2017) | [10] |
| CHL73 | R709/R665 | LR | OLCI | 5.99–117.54 | Manguaba | Brazil | Lins et al. (2017) | [10] |
| CHL74 | R705/R665 | LR | MSI | 5.99–117.54 | Manguaba | Brazil | Lins et al. (2017) | [10] |
| CHL75 | (1/R681-1/R709)/R674 | LR | OLCI | 5.99–117.54 | Manguaba | Brazil | Lins et al. (2017) | [10] |
| CHL79 | (1/R650-1/R710)·R740 | LR | 4.4–3078 | National Warm-water Aquaculture Center, Stonevill | USA | Zimba, Gitelson (2006) | [11] | |
| CHL80 | (R485-R660)/R560 | LR | LS TM | 3.0–7.0 | Lake Kinneret | Israel | Mayo et al. (1995) | [131] |
| CHL81 | log(R710/R670) | LR | CASI-2 | Barton Broad | UK | Hunter et al. (2008) | [128] | |
| CHL82 | log(R483)/log(R660) | LR | LS ETM+ | 1.14–23.23 | Pensacola Bay | Florida | Han, Jordan (2005) | [132] |
| CHL83 | R483/R660 | LT-LR | LS TM | 2.1–183 | Minnesota lakes | USA | Brezonik et al. (2005) | [102] |
| CHL84 | R483/R660 | LR | LS TM | 2.1–183 | Minnesota lakes | USA | Brezonik et al. (2005) | [102] |
| CHL85 | R830/(R485+R560+R830) | LR | LS TM | 1.8–18 | Sweden | Lindell et al. (1999) | [54] | |
| CHL86 | R660/R565 | LR | LS TM | 66.0–188.59 | Lake Reelfoot | USA | Wang et al. (2006) | [74] |
| CHL87 | R700/R670 | LR | Radiometric | 2–79 | Tennessee | USA | Dierberg, Carriker (1994) | [89] |
| CHL88 | R702/R674 | LR | AISA | 2.6–100 | Finnish lakes | Finland | Kutser et al. (1999) | [63] |
| CHL89 | R681-R665-(R709-R665)·((681-665)/(709-665)) | LR | MERIS | Gower et al. (1999) | [94] | |||
| CHL90 | (1/R662-1/R693)/(1/R740-1/705) | LR | 0.98–89.23 | Lake Taihu | China | Le et al. (2009) | [12] | |
| CHL91 | R708/R665 | LR | MERIS | 1.0–100 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| CHL92 | R710/R688 | LR | AISA | 1.0–100 | Finnish lakes | Finland | Kallio et al. (2001) | [110] |
| CHL93 | R719/R667 | LR | Radiometric | 0–0.2 | Lake Tai | China | Jiao et al. (2006) | [133] |
| CHL94 | R550/R590 | LR | Radiometric | 0.6–70 | Baltic Sea | Darecki et al. (2003) | [72] | |
| CHL95 | R555/R645 | LR | MODIS | 1–100 | Baltic Sea | Woźniak (2014) | [113] | |
| CHL96 | (1/R681-1/R709)/(1/R753-1/R709) | LR | MERIS | Zhou (2011) | [95] | |||
| CHL97 | (1/R705-1/R665)/(1/R705+1/R665) | LR | MERIS | 1–60 | Mishra, Mishra (2012) | [62] | ||
| CHL98 | (1/R670-1/R710)·R750 | LR | Radiometric | 2.07–183.5 | Fremont State lakes | USA | Gitelson et al. (2009) | [64] |
| CHL99 | log(max(R443/R560, R490/R560, R510/R560)) | P4R | MERIS | OC4E for MERIS | ||||
| CHL100 | log(max(R443/R547, R488/R547)) | P4R | MODIS | OC3M for MODIS | ||||
| CHL101 | R709-R681-(709-681)/(753-681)·(R753-R681) | LR | MERIS | Gower et al. (2008) | [61] | |||
| CHL102 | max(R670-R850) | LR | Radiometric | 20–280 | Lake Carter | USA | Schalles et al. (1998) | [129] |
| ZSD103 | R560 | LLR | LS TM | 0.5–9.0 | Lake Michigan | USA | Lathrop, Lillesand (1986) | [127] |
| ZSD104 | R485/R660, R485 | LR-MLR | TS TM | ~0.5–5 | Minnesota lakes | USA | Kloiber et al. (2002) | [69] |
| ZSD105 | R485/R560 | LR | LS TM | 4.6–6.8 | Lake Iseo | Italy | Giardino et al. (2001) | [134] |
| ZSD106 | (R488-R748)/(R667-R748) | LR | LS TM | 0.4–7.0 | Southern lakes | Finland | Härma et al. (2001) | [109] |
| ZSD107 | R560, R660 | MLR | LS TM | 0.16-0.33 | Reelfoot Lake | USA | Wang et al. (2006) | [74] |
| ZSD109 | R660 | LLR | LS TM | 0.45–2 | New York Harbour | USA | Hellweger et al. (2004) | [71] |
| ZSD110 | R485/R660 | LR | LS ETM+ | 0.5–5.5 | Southern Lakes | Finland | Kallio et al. (2008) | [99] |
| ZSD111 | R660/R560 | LT-LR | LS TM | 0.22–0.79 | Lake Chagan, Xinmiao, Kuli | China | Duan et al. (2009) | [135] |
| ZSD112 | ln(R555)/R488, (R645+R858)/R469, R555 | MLR | MODIS | 0.25–1.2 | Chaohu Lake | China | Wu et al. (2009) | [70] |
| ZSD113 | R490/R620 | LT-LR | MERIS | 3.0–6.0 | Himmerf-Järden Bay | Sweden | Kratzer et al. (2008) | [24] |
| ZSD114 | R560/R709 | LLR | OLCI | (turbid waters) | Baltic Sea | Estonia | Alikas, Kratzer (2017) | [25] |
| ZSD115 | R490/R709 | LLR | OLCI | (clear waters) | Baltic Sea | Estonia | Alikas, Kratzer (2017) | [25] |
| CDOM116 | R670/R412 | LR | Radiometric | 0.1–1.5 (440 nm) | Clyde Sea | Scotland | Bowers et al. (2000) | [136] |
| CDOM117 | R485, R485/R830 | LT-MLR | LS TM | 0.6–19.4 (440 nm) | Minnesota lakes | USA | Brezonik et al. (2005) | [102] |
| CDOM118 | R443/R510 | LTLR | SeaWiFS | 0.07–1.1 (412 nm) | Gulf of Mexico | USA | D’Sa, Miller (2003) | [137] |
| CDOM119 | R664/R550 | LR | MERIS | 1.13–2.07 (420 nm) | Lake Mälaren | Sweden | Ammenberg et al. (2002) | [68] |
| CDOM120 | R565/R660 | LR | ALI | 0.68–11.1 (420 nm) | Finnish and Sweden lakes | Kutser et al. (2005) | [98] | |
| CDOM121 | R565/R660 | LLR | ALI | 0.68–11.1 (420 nm) | Finnish and Sweden lakes | Kutser et al. (2005) | [98] | |
| CDOM122 | R670/R550 | LLR | 0.35–11.9 (440 nm) | Minnesota lakes | USA | Menken et al. (2006) | [67] | |
| CDOM123 | R700/R670 | LR | 0.35–11.9 (440 nm) | Minnesota lakes | USA | Menken et al. (2006) | [67] | |
| CDOM124 | R570/R655 | LLR | Radiometric | 0.23–17.4 (440 nm) | Pomeranian lakes, Baltic Sea | Poland | Ficek et al. (2011) | [75] |
| CDOM125 | R412/R510 | LLR | SeaWiFS | 0.07–1.1 (412 nm) | Gulf of Mexico | USA | D’Sa, Miller (2003) | [137] |
| CDOM126 | R510/R590 | LLR | SeaWiFS | 0.07–1.1 (412 nm) | Gulf of Mexico | USA | D’Sa, Miller (2003) | [137] |
| CDOM127 | R400/R600 | LLR | Radiometric | 0.1–1.9 (440 nm) | Tamar Estuary | UK | Doxaran et al. (2005) | [97] |
| CDOM128 | R665/R490 | LR | AISA | 1.29–2.61 (400 nm) | Gulf of Finland | Finland | Koponen et al. (2007) | [91] |
| CDOM129 | R560/R660 | LR | LS ETM+ | 1.1–12.2 (400 nm) | Finnish lakes and rivers | Finland | Kallio et al. (2008) | [99] |
| CDOM130 | (R480-R700/R675-R520)/(R480-R700/R675+R520) | LLR | Radiometric | 0.1–12 (380 nm) | Hungarian, Bulgarian, German lakes | Gitelson et al. (1993) | [112] | |
| CDOM131 | R560/R660 | LLR | LS ETM+ | 1–12.2 (400 nm) | Finnish lakes | Finland | Kallio et al. (2008) | [99] |
| CDOM132 | R412+R700/R670 | MLR | 0.35–11.9 (440 nm) | Minnesota lakes | USA | Menken et al. (2006) | [67] | |
| CDOM133 | R660, R560/R485 | LT-MLR | LS TM | 1.38–6.45 (400 nm) | Kolyma River | Russia | Griffin et al. (2011) | [138] |
| CDOM134 | log(R490/R550) | LT-P2R | MODIS; MERIS, SeaWiFS | 0.4–2 (400 nm) | Baltic Sea | Poland | Kowalczuk et al. (2005) | [139] |
| CDOM135 | R510/R753.75 | LLR | OLCI | 0.51–25.1 (440 nm) | Lakes and rivers | USA | Brezonik et al. (2015) | [100] |
| CDOM136 | R490/R740 | LLR | MSI | 0.51–25.1 (440 nm) | Lakes and rivers | USA | Brezonik et al. (2015) | [100] |
Appendix B




Appendix C
| Symbol | Meaning |
|---|---|
| OWT | Optical water type |
| OSC | Optically significant constituent |
| R(λ) | Water-leaving reflectance |
| TSM | Total suspended matter, mg·L−1 |
| SPIM | Suspended particulate inorganic matter, mg·L−1 |
| SPOM | Suspended particulate organic matter, mg·L−1 |
| CDOM | Coloured dissolved organic matter |
| aCDOM(442) | Absorption coefficient of CDOM at a wavelength of 442 nm, m−1 |
| Chl-a | Chlorophyll-a, mg·m−3 |
| ZSD | Secchi disk depth, m |
| NIR | Near-infrared |
| SRF | Spectral response function |
| MSI | Multispectral Instrument |
| OLCI | Ocean and Land Colour Instrument |
| MERIS | Medium Resolution Imaging Spectrometer |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| ALI | Advanced Land Imager |
| LS TM | Landsat Thematic Mapper |
| LS ETM+ | Landsat Enhanced Thematic Mapper Plus |
| AISA | The Airborne Imaging Spectrometer for Applications |
| SPOT | Satellite Pour l’Observation de la Terre (in French) |
| SEVIR | Spinning Enhanced Visible and Infrared Imager |
| GOCI | Geostationary Ocean Color Imager |
| WV2 | WorldView-2 |
| CASI | Compact Airborne Spectrographic Imager |
| AMMS | Airborne Multispectral Measurement System |
| SeaWiFS | Sea-viewing Wide Field-of-view Sensor |
| LR | Linear regression |
| MLR | Multiple linear regression |
| LT-LR | Log-transformed linear regression |
| LT-MLR | Log-transformed multiple linear regression |
| LLR | Log-log regression |
| P2R | Polynomial regression (number indicated degree of polynomial) |
| LT10-LR | Log-transformed linear regression with base 10 |
| LL10R | Log-log regression with base 10 |
| LT-P2R | Log-transformed polynomial regression |
References
- The European Parliament; The Council of of the E.U. WFD Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for Community action in the field of water policy. Off. J. Eur. Parliam. 2000, 327, 1–73. [Google Scholar]
- Carstensen, J.; Klais, R.; Cloern, J.E. Phytoplankton blooms in estuarine and coastal waters: Seasonal patterns and key species. Estuar. Coast. Shelf Sci. 2015, 162, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Jickells, T. External inputs as a contributor to eutrophication problems. J. Sea Res. 2005, 54, 58–69. [Google Scholar] [CrossRef]
- Gustafsson, B.G.; Schenk, F.; Blenckner, T.; Eilola, K.; Meier, H.E.M.; Müller-Karulis, B.; Neumann, T.; Ruoho-Airola, T.; Savchuk, O.P.; Zorita, E. Reconstructing the Development of Baltic Sea Eutrophication 1850–2006. AMBIO 2012, 41, 534–548. [Google Scholar] [CrossRef] [Green Version]
- Diaz, R.J.; Rosenberg, R. Spreading Dead Zones and Consequences for Marine Ecosystems. Science (80-) 2008, 321, 926–929. [Google Scholar] [CrossRef]
- Voss, M.; Dippner, J.W.; Humborg, C.; Hürdler, J.; Korth, F.; Neumann, T.; Schernewski, G.; Venohr, M. History and scenarios of future development of Baltic Sea eutrophication. Estuar. Coast. Shelf Sci. 2011, 92, 307–322. [Google Scholar] [CrossRef]
- Dickey, T.; Lewis, M.; Chang, G. Optical oceanography: Recent advances and future directions using global remote sensing and in situ observations. Rev. Geophys. 2006, 44, RG1001. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: San Diego, CA, USA, 1994; ISBN 0-12-502750-8. [Google Scholar]
- Gordon, H.R.; Morel, A.Y. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review; Lecture Notes on Coastal and Estuarine Studies; American Geophysical Union: Washington, DC, USA, 1983; Volume 4, ISBN 0-387-90923-0. [Google Scholar]
- Lins, R.; Martinez, J.-M.; Motta Marques, D.; Cirilo, J.; Fragoso, C. Assessment of Chlorophyll-a Remote Sensing Algorithms in a Productive Tropical Estuarine-Lagoon System. Remote Sens. 2017, 9, 516. [Google Scholar] [CrossRef] [Green Version]
- Zimba, P.V.; Gitelson, A. Remote estimation of chlorophyll concentration in hyper-eutrophic aquatic systems: Model tuning and accuracy optimization. Aquaculture 2006, 256, 272–286. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Raag, L.; Sipelgas, L.; Uiboupin, R. Analysis of natural background and dredging-induced changes in TSM concentration from MERIS images near commercial harbours in the Estonian coastal sea. Int. J. Remote Sens. 2014, 35, 6764–6780. [Google Scholar] [CrossRef]
- Kyryliuk, D.; Kratzer, S. Total suspended matter derived from MERIS data as indicator for coastal processes in the Baltic Sea. Ocean Sci. Discuss. 2016, 1–30. [Google Scholar] [CrossRef]
- Pozdnyakov, D.; Grassl, H. Colour of Inland and Coastal Waters. A Metgodology for Its Interpretation; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-540-00200-0. [Google Scholar]
- Leppäranta, M.; Myrberg, K. Physical Oceanography of the Baltic Sea; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-79702-9. [Google Scholar]
- Shi, W.; Zhang, Y.; Wang, M. Deriving Total Suspended Matter Concentration from the Near-Infrared-Based Inherent Optical Properties over Turbid Waters: A Case Study in Lake Taihu. Remote Sens. 2018, 10, 333. [Google Scholar] [CrossRef] [Green Version]
- Brando, V.E.; Anstee, J.M.; Wettle, M.; Dekker, A.G.; Phinn, S.R.; Roelfsema, C. A physics based retrieval and quality assessment of bathymetry from suboptimal hyperspectral data. Remote Sens. Environ. 2009, 113, 755–770. [Google Scholar] [CrossRef]
- Tzortziou, M.; Zeri, C.; Dimitriou, E.; Ding, Y.; Jaffé, R.; Anagnostou, E.; Pitta, E.; Mentzafou, A. Colored dissolved organic matter dynamics and anthropogenic influences in a major transboundary river and its coastal wetland. Limnol. Oceanogr. 2015, 60, 1222–1240. [Google Scholar] [CrossRef]
- Markager, S.; Vincent, W.F. Spectral light attenuation and the absorption of UV and blue light in natural waters. Limnol. Oceanogr. 2000, 45, 642–650. [Google Scholar] [CrossRef]
- Menon, H.B.; Sangekar, N.P.; Lotliker, A.A.; Vethamony, P. Dynamics of chromophoric dissolved organic matter in Mandovi and Zuari estuaries—A study through in situ and satellite data. ISPRS J. Photogramm. Remote Sens. 2011, 66, 545–552. [Google Scholar] [CrossRef]
- Matsuoka, A.; Hooker, S.B.; Bricaud, A.; Gentili, B.; Babin, M. Estimating absorption coefficients of colored dissolved organic matter (CDOM) using a semi-analytical algorithm for southern Beaufort Sea waters: Application to deriving concentrations of dissolved organic carbon from space. Biogeosciences 2013, 10, 917–927. [Google Scholar] [CrossRef] [Green Version]
- Preisendorfer, R.W. Secchi disk science: Visual optics of natural waters1. Limnol. Oceanogr. 1986, 31, 909–926. [Google Scholar] [CrossRef] [Green Version]
- Kratzer, S.; Brockmann, C.; Moore, G. Using MERIS full resolution data to monitor coastal waters–A case study from Himmerfjärden, a fjord-like bay in the northwestern Baltic Sea. Remote Sens. Environ. 2008, 112, 2284–2300. [Google Scholar] [CrossRef]
- Alikas, K.; Kratzer, S. Improved retrieval of Secchi depth for optically-complex waters using remote sensing data. Ecol. Indic. 2017, 77, 218–227. [Google Scholar] [CrossRef]
- ESA Sentinel Online. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi (accessed on 27 January 2020).
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First Experiences in Mapping Lake Water Quality Parameters with Sentinel-2 MSI Imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef] [Green Version]
- Dogliotti, A.; Gossn, J.; Vanhellemont, Q.; Ruddick, K. Detecting and Quantifying a Massive Invasion of Floating Aquatic Plants in the Río de la Plata Turbid Waters Using High Spatial Resolution Ocean Color Imagery. Remote Sens. 2018, 10, 1140. [Google Scholar] [CrossRef] [Green Version]
- Soriano-González, A.; Fernández-Tejedor, D. Alcaraz First Results of Phytoplankton Spatial Dynamics in Two NW-Mediterranean Bays from Chlorophyll-a Estimates Using Sentinel 2: Potential Implications for Aquaculture. Remote Sens. 2019, 11, 1756. [Google Scholar] [CrossRef] [Green Version]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef] [Green Version]
- Caballero, I.; Stumpf, R.; Meredith, A. Preliminary Assessment of Turbidity and Chlorophyll Impact on Bathymetry Derived from Sentinel-2A and Sentinel-3A Satellites in South Florida. Remote Sens. 2019, 11, 645. [Google Scholar] [CrossRef] [Green Version]
- Ruescas, A.B.; Hieronymi, M.; Mateo-Garcia, G.; Koponen, S.; Kallio, K.; Camps-Valls, G. Machine learning regression approaches for colored dissolved organic matter (CDOM) retrieval with S2-MSI and S3-OLCI simulated data. Remote Sens. 2018, 10, 786. [Google Scholar] [CrossRef] [Green Version]
- Poddar, S.; Chacko, N.; Swain, D. Estimation of Chlorophyll-a in Northern Coastal Bay of Bengal Using Landsat-8 OLI and Sentinel-2 MSI Sensors. Front. Mar. Sci. 2019, 6, 598. [Google Scholar] [CrossRef]
- Ligi, M.; Kutser, T.; Kallio, K.; Attila, J.; Koponen, S.; Paavel, B.; Soomets, T.; Reinart, A. Testing the performance of empirical remote sensing algorithms in the Baltic Sea waters with modelled and in situ reflectance data. Oceanologia 2017, 59, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Ohde, T.; Siegel, H.; Gerth, M. Validation of MERIS Level-2 products in the Baltic Sea, the Namibian coastal area and the Atlantic Ocean. Int. J. Remote Sens. 2007, 28, 609–624. [Google Scholar] [CrossRef]
- Harvey, T. Bio-Optics, Satellite Remote Sensing and Baltic Sea Ecosystems: Applications for Monitoring and Management; Stockholm University: Stockholm, Sweden, 2015. [Google Scholar]
- Grendaitė, D.; Stonevičius, E.; Karosienė, J.; Savadova, K.; Kasperovičienė, J. Chlorophyll-a concentration retrieval in eutrophic lakes in Lithuania from Sentinel-2 data. Geol. Geogr. 2018, 4, 15–28. [Google Scholar] [CrossRef]
- Barale, V.; Schlittenhardt, P.M. (Eds.) Ocean Colour: Theory and Applications in a Decade of CZCS Experience; Eurocourses: Remote Sensing; Springer: Dordrecht, The Netherlands, 1993; Volume 3, ISBN 978-94-010-4788-3. [Google Scholar]
- IOCCG. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex, Waters; IOCCG: Dartmounth, NS, Canada, 2000; Volume 3. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Moore, T.S.; Dowell, M.D.; Bradt, S.; Ruiz Verdu, A. An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 2014, 143, 97–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mélin, F.; Vantrepotte, V.; Clerici, M.; D’Alimonte, D.; Zibordi, G.; Berthon, J.-F.; Canuti, E. Multi-sensor satellite time series of optical properties and chlorophyll-a concentration in the Adriatic Sea. Prog. Oceanogr. 2011, 91, 229–244. [Google Scholar] [CrossRef]
- Ye, H.; Li, J.; Li, T.; Shen, Q.; Zhu, J.; Wang, X.; Zhang, F.; Zhang, J.; Zhang, B. Spectral Classification of the Yellow Sea and Implications for Coastal Ocean Color Remote Sensing. Remote Sens. 2016, 8, 321. [Google Scholar] [CrossRef] [Green Version]
- Vantrepotte, V.; Loisel, H.; Dessailly, D.; Mériaux, X. Optical classification of contrasted coastal waters. Remote Sens. Environ. 2012, 123, 306–323. [Google Scholar] [CrossRef]
- Uudeberg, K.; Ansko, I.; Põru, G.; Ansper, A.; Reinart, A. Using Optical Water Types to Monitor Changes in Optically Complex Inland and Coastal Waters. Remote Sens. 2019, 11, 2297. [Google Scholar] [CrossRef] [Green Version]
- Zhurbas, V.; Laanemets, J.; Vantera, E. Modeling of the mesoscale structure of coupled upwelling/downwelling events and the related input of nutrients to the upper mixed layer in the Gulf of Finland, baltic sea. J. Geophys. Res. Ocean. 2008, 113, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Uiboupin, R.; Laanemets, J. Upwelling characteristics derived from satellite sea surface temperature data in the Gulf of Finland, Baltic sea. Boreal Environ. Res. 2009, 14, 297–304. [Google Scholar]
- Tilstone, G.H.; Moore, G.F.; Doerffer, R.; Røttgers, R.; Ruddick, K.G.; Pasterkamp, R.; Jørgensen, P.V. Regional Validation of MERIS Chlorophyll products in North Sea REVAMP Protocols Regional Validation of MERIS Chlorophyll products. In Proceedings of the Working meeting on MERIS and AATSR Calibration and Geophysical Validation (ENVISAT MAVT-2003), Frascati, Italy, 20–24 October 2003. [Google Scholar]
- MSI SRFs. Available online: https://earth.esa.int/web/sentinel/user-guides/sentinel-2-msi/document-library/-/asset_publisher/Wk0TKajiISaR/content/sentinel-2a-spectral-responses (accessed on 24 July 2019).
- OLCI SRFs. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-olci/olci-instrument/spectral-response-function-data (accessed on 24 July 2019).
- The International Organization for Standardization. ISO 5667-3:2018 Water Quality—Sampling—Part 3: Preservation and Handling of Water Samples; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- The International Organization for Standardization. ISO 10260:1992 Water quality—Measurement of Biochemical Parameters—Spectrometric Determination of the Chlorophyll-a Concentration; ISO: Geneva, Switzerland, 1992. [Google Scholar]
- Jeffrey, S.W.; Humphrey, G.F. New spectrophotometric equations for determining chlorophylls a, b, c1 and c2 in higher plants, algae and natural phytoplankton. Biochem. Physiol. Pflanz. 1975, 167, 191–194. [Google Scholar] [CrossRef]
- Lindell, T.; Pierson, D.; Premazzi, G.; Zilioti, E. Manual for Monitoring European Lakes Using Remote Sensing Techniques; EU: Brussels, Belgium, 1999; ISBN 928285390X. [Google Scholar]
- Lorenzen, C.J. Determination of Chlorophyll and Pheo-pigments: Spectrophotometric Equations. Limnol. Oceanogr. 1967, 12, 343–346. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling, 1st ed.; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6848-6. [Google Scholar]
- Kuhn, M. The Caret Package. Available online: http://topepo.github.io/caret/index.html (accessed on 21 January 2020).
- Metrics. Available online: https://cran.r-project.org/web/packages/Metrics/ (accessed on 2 February 2020).
- ESTHub Processing Platform. Available online: https://ehcalvalus.maaamet.ee/calest/calvalus.jsp (accessed on 9 February 2020).
- GITELSON, A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Goncalves, P. Global monitoring of plankton blooms using MERIS MCI. Int. J. Remote Sens. 2008, 29, 6209–6216. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Kutser, T.; Kallio, K.; Eloheimo, K.; Hannonen, T.; Pyhälahti, T.; Koponen, S.; Pulliainen, J. Quantitative monitoring of water properities with the airborne imaging spectrometer AISA. Proc. Est. Acad. Sci. Biol. Ecol. 1999, 48, 25–36. [Google Scholar]
- Gitelson, A.A.; Gurlin, D.; Moses, W.J.; Barrow, T. A bio-optical algorithm for the remote estimation of the chlorophyll- a concentration in case 2 waters. Environ. Res. Lett. 2009, 4, 045003. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote Sensing of Black Lakes and Using 810 nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, J.; Dong, Q.; Song, Q.T.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Menken, K.D.; Brezonik, P.L.; Bauer, M.E. Influence of chlorophyll and colored dissolved organic matter (CDOM) on lake reflectance spectra: Implications for measuring lake properties by remote sensing. Lake Reserv. Manag. 2006, 22, 179–190. [Google Scholar] [CrossRef] [Green Version]
- Ammenberg, P.; Flink, P.; Lindell, T.; Pierson, D.; Strömbeck, N. Bio-optical modelling combined with remote sensing to assess water quality. Int. J. Remote Sens. 2002, 23, 1621–1638. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Brezonik, P.L.; Bauer, M.E. Application of Landsat imagery to regional-scale assessments of lake clarity. Water Res. 2002, 36, 4330–4340. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, W.; Wang, X.; Luo, D. Application of MODIS satellite data in monitoring water quality parameters of Chaohu Lake in China. Environ. Monit. Assess. 2009, 148, 255–264. [Google Scholar] [CrossRef]
- Hellweger, F.L.; Schlosser, P.; Lall, U.; Weissel, J.K. Use of satellite imagery for water quality studies in New York Harbor. Estuar. Coast. Shelf Sci. 2004, 61, 437–448. [Google Scholar] [CrossRef]
- Darecki, M.; Weeks, A.; Sagan, S.; Kowalczuk, P.; Kaczmarek, S. Optical characteristics of two contrasting Case 2 waters and their influence on remote sensing algorithms. Cont. Shelf Res. 2003, 23, 237–250. [Google Scholar] [CrossRef]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Han, L.; Kung, H.T.; van Arsdale, R.B. Applications of Landsat-5 TM imagery in assessing and mapping water quality in Reelfoot Lake, Tennessee. Int. J. Remote Sens. 2006, 27, 5269–5283. [Google Scholar] [CrossRef]
- Ficek, D.; Zapadka, T.; Dera, J. Remote sensing reflectance of Pomeranian lakes and the Baltic. Oceanologia 2011, 53, 959–970. [Google Scholar] [CrossRef] [Green Version]
- Simis, S.G.H.; Ylöstalo, P.; Kallio, K.Y.; Spilling, K.; Kutser, T. Contrasting seasonality in optical-biogeochemical properties of the Baltic Sea. PLoS ONE 2017, 12, e0173357. [Google Scholar] [CrossRef]
- Soomets; Uudeberg; Jakovels; Zagars; Reinart; Brauns; Kutser Comparison of Lake Optical Water Types Derived from Sentinel-2 and Sentinel-3. Remote Sens. 2019, 11, 2883. [CrossRef] [Green Version]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Advantages of high quality SWIR bands for ocean colour processing: Examples from Landsat-8. Remote Sens. Environ. 2015, 161, 89–106. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Li, W.; Gatebe, C.K.; Jamet, C.; Zibordi, G.; Schroeder, T.; Stamnes, K. Atmospheric correction over coastal waters using multilayer neural networks. Remote Sens. Environ. 2017, 199, 218–240. [Google Scholar] [CrossRef]
- Harmel, T.; Chami, M.; Tormos, T.; Reynaud, N.; Danis, P.-A. Sunglint correction of the Multi-Spectral Instrument (MSI)-SENTINEL-2 imagery over inland and sea waters from SWIR bands. Remote Sens. Environ. 2018, 204, 308–321. [Google Scholar] [CrossRef]
- Martins, V.; Barbosa, C.; de Carvalho, L.; Jorge, D.; Lobo, F.; Novo, E. Assessment of Atmospheric Correction Methods for Sentinel-2 MSI Images Applied to Amazon Floodplain Lakes. Remote Sens. 2017, 9, 322. [Google Scholar] [CrossRef] [Green Version]
- De Keukelaere, L.; Sterckx, S.; Adriaensen, S.; Knaeps, E.; Reusen, I.; Giardino, C.; Bresciani, M.; Hunter, P.; Neil, C.; Van der Zande, D.; et al. Atmospheric correction of Landsat-8/OLI and Sentinel-2/MSI data using iCOR algorithm: Validation for coastal and inland waters. Eur. J. Remote Sens. 2018, 51, 525–542. [Google Scholar] [CrossRef] [Green Version]
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; et al. Laboratory Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range. Remote Sens. 2019, 11, 1101. [Google Scholar] [CrossRef] [Green Version]
- Vabson, V.; Kuusk, J.; Ansko, I.; Vendt, R.; Alikas, K.; Ruddick, K.; Ansper, A.; Bresciani, M.; Burmester, H.; Costa, M.; et al. Field Intercomparison of Radiometers Used for Satellite Validation in the 400–900 nm Range. Remote Sens. 2019, 11, 1129. [Google Scholar] [CrossRef] [Green Version]
- Alikas, K.; Ansko, I.; Vabson, V.; Ansper, A.; Kangro, K.; Uudeberg, K.; Ligi, M. Consistency of Radiometric Satellite Data over Lakes and Coastal Waters with Local Field Measurements. Remote Sens. 2020, 12, 616. [Google Scholar] [CrossRef] [Green Version]
- Flink, P.; Lindell, L.T.; Östlund, C. Statistical analysis of hyperspectral data from two Swedish lakes. Sci. Total Environ. 2001, 268, 155–169. [Google Scholar] [CrossRef]
- Duan, H.; Zhang, Y.; Zhang, B.; Song, K.; Wang, Z. Assessment of chlorophyll-a concentration and trophic state for lake chagan using landsat TM and field spectral data. Environ. Monit. Assess. 2007, 129, 295–308. [Google Scholar] [CrossRef] [PubMed]
- Dierberg, F.E.; Carriker, N.E. Field testing two instruments for remotely sensing water quality in the Tennessee Valley. Environ. Sci. Technol. 1994, 28, 16–25. [Google Scholar] [CrossRef] [PubMed]
- Gons, H.J. Optical Teledetection of Chlorophyll a in Turbid Inland Waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Koponen, S.; Attila, J.; Pulliainen, J.; Kallio, K.; Pyhälahti, T.; Lindfors, A.; Rasmus, K.; Hallikainen, M. A case study of airborne and satellite remote sensing of a spring bloom event in the Gulf of Finland. Cont. Shelf Res. 2007, 27, 228–244. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Estimation of chlorophyll- a concentration in case II waters using MODIS and MERIS data—successes and challenges. Environ. Res. Lett. 2009, 4, 045005. [Google Scholar] [CrossRef] [Green Version]
- Matthews, M.W. A current review of empirical procedures of remote sensing in Inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Gower, J.F.R.; Doerffer, R.; Borstad, G.A. Interpretation of the 685nm peak in water-leaving radiance spectra in terms of fluorescence, absorption and scattering, and its observation by MERIS. Int. J. Remote Sens. 1999, 20, 1771–1786. [Google Scholar] [CrossRef]
- Zhou, L. Remote Sensing Retrieval of Chlorophyll-a Concentration in Lake Waters; Chinese Academy of Sciences: Beijing, China, 2011. [Google Scholar]
- Doxaran, D.; Froidefond, J.-M.; Castaing, P. Remote-sensing reflectance of turbid sediment-dominated waters Reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Appl. Opt. 2003, 42, 2623. [Google Scholar] [CrossRef]
- Doxaran, D.; Cherukuru, R.C.N.; Lavender, S.J. Use of reflectance band ratios to estimate suspended and dissolved matter concentrations in estuarine waters. Int. J. Remote Sens. 2005, 26, 1763–1769. [Google Scholar] [CrossRef]
- Kutser, T.; Pierson, D.C.; Kallio, K.Y.; Reinart, A.; Sobek, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Kallio, K.; Attila, J.; Härmä, P.; Koponen, S.; Pulliainen, J.; Hyytiäinen, U.M.; Pyhälahti, T. Landsat ETM+ images in the estimation of seasonal lake water quality in boreal river basins. Environ. Manag. 2008, 42, 511–522. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors affecting the measurement of CDOM by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Feng, H. A fuzzy logic classification scheme for selecting and blending satellite ocean color algorithms. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1764–1776. [Google Scholar] [CrossRef]
- Bi, S.; Li, Y.; Xu, J.; Liu, G.; Song, K.; Mu, M.; Lyu, H.; Miao, S.; Xu, J. Optical classification of inland waters based on an improved Fuzzy C-Means method. Opt. Express 2019, 27, 34838. [Google Scholar] [CrossRef]
- Petus, C.; Chust, G.; Gohin, F.; Doxaran, D.; Froidefond, J.-M.; Sagarminaga, Y. Estimating turbidity and total suspended matter in the Adour River plume (South Bay of Biscay) using MODIS 250-m imagery. Cont. Shelf Res. 2010, 30, 379–392. [Google Scholar] [CrossRef] [Green Version]
- Chavula, G.; Brezonik, P.; Thenkabail, P.; Johnson, T.; Bauer, M. Estimating chlorophyll concentration in Lake Malawi from MODIS satellite imagery. Phys. Chem. Earth 2009, 34, 755–760. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. A reflectance band ratio used to estimate suspended matter concentrations in sediment-dominated coastal waters. Int. J. Remote Sens. 2002, 23, 5079–5085. [Google Scholar] [CrossRef]
- Härmä, P.; Vepsäläinen, J.; Hannonen, T.; Pyhälahti, T.; Kämäri, J.; Kallio, K.; Eloheimo, K.; Koponen, S. Detection of water quality using simulated satellite data and semi-empirical algorithms in Finland. Sci. Total Environ. 2001, 268, 107–121. [Google Scholar] [CrossRef]
- Kallio, K.; Kutser, T.; Hannonen, T.; Koponen, S.; Pulliainen, J.; Vepsäläinen, J.; Pyhälahti, T. Retrieval of water quality from airborne imaging spectrometry of various lake types in different seasons. Sci. Total Environ. 2001, 268, 59–77. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Gitelson, A.; Garbuzov, G.; Szilagyi, F.; Mittenzwey, K.H.; Karnieli, A.; Kaiser, A. Quantitative remote sensing methods for real-time monitoring of inland waters quality. Int. J. Remote Sens. 1993, 14, 1269–1295. [Google Scholar] [CrossRef]
- Woźniak, S.B. Simple statistical formulas for estimating biogeochemical properties of suspended particulate matter in the southern baltic sea potentially useful for optical remote sensing applications. Oceanologia 2014, 56, 7–39. [Google Scholar] [CrossRef] [Green Version]
- Dekker, A.G.; Vos, R.J.; Peters, S.W.M. Analytical algorithms for lake water tsm estimation for retrospective analyses of tm and spot sensor data. Int. J. Remote Sens. 2002, 23, 15–35. [Google Scholar] [CrossRef]
- Neukermans, G.; Ruddick, K.; Bernard, E.; Ramon, D.; Nechad, B.; Deschamps, P.-Y. Mapping total suspended matter from geostationary satellites: A feasibility study with SEVIRI in the Southern North Sea. Opt. Express 2009, 17, 14029. [Google Scholar] [CrossRef] [Green Version]
- Ouillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.M.; Andréfouët, S.; Muñoz-Caravaca, A. Optical algorithms at satellite wavelengths for total suspended matter in tropical coastal waters. Sensors 2008, 8, 4165–4185. [Google Scholar] [CrossRef]
- He, A.; He, X.; Bai, Y.; Zhu, Q.; Gong, F.; Huang, H.; Pan, D. Simulation of sedimentation in Lake Taihu with Geostationary Satellite Ocean Color Data. Remote Sens. 2019, 11, 379. [Google Scholar] [CrossRef] [Green Version]
- Molkov, A.A.; Fedorov, S.V.; Pelevin, V.V.; Korchemkina, E.N. Regional Models for High-Resolution Retrieval of Chlorophyll a and TSM Concentrations in the Gorky Reservoir by Sentinel-2 Imagery. Remote Sens. 2019, 11, 1215. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Mao, Z.; Wang, Z. Retrieval of total suspended matter concentrations from high resolution WorldView-2 imagery: A case study of inland rivers. IOP Conf. Ser. Earth Environ. Sci. 2018, 121, 032036. [Google Scholar] [CrossRef]
- Han, Z.; Jin, Y.-Q.; Yun, C.-X. Suspended sediment concentrations in the Yangtze River estuary retrieved from the CMODIS data. Int. J. Remote Sens. 2006, 27, 4329–4336. [Google Scholar] [CrossRef]
- Tassan, S. An improved in-water algorithm for the determination of chlorophyll and suspended sediment concentration from thematic mapper data in coastal waters. Int. J. Remote Sens. 1993, 14, 122–1229. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Satellite Estimation of Chlorophyll-a Concentration Using the Red and NIR Bands of MERIS—The Azov Sea Case Study. IEEE Geosci. Remote Sens. Lett. 2009, 6, 845–849. [Google Scholar] [CrossRef]
- Brivio, P.A.; Giardino, C.; Zilioli, E. Determination of chlorophyll concentration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images. Int. J. Remote Sens. 2001, 22, 487–502. [Google Scholar] [CrossRef]
- Dwivedi, R.M.; Narain, A. Remote sensing of phytoplankton an attempt from the Landsat Thematic Mapper. Int. J. Remote Sens. 1987, 8, 1563–1569. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Yacobi, Y.Z.; Karnieli, A.; Kress, N. Reflectance spectra of polluted marine waters in Haifa Bay, Southeastern Mediterranean: Features and application for remote estimation of chlorophyll concentration. Isr. J. Earth Sci. 1996, 45, 127–136. [Google Scholar]
- Yacobi, Y.Z.; Gitelson, A.; Mayo, M. Remote sensing of chlorophyll in Lake Kinneret using highspectral-resolution radiometer and Landsat TM: Spectral features of reflectance and algorithm development. J. Plankton Res. 1995, 17, 2155–2173. [Google Scholar] [CrossRef] [Green Version]
- Lathrop, R.G.; Lillesand, T.M. Use of Thematic Mapper data to assess water quality in Green Bay and central Lake Michigan. Photogramm. Eng. Remote Sens. 1986, 52, 671–680. [Google Scholar]
- Hunter, P.D.; Tyler, A.N.; Willby, N.J.; Gilvear, D.J. The spatial dynamics of vertical migration by Microcystis aeruginosa in a eutrophic shallow lake: A case study using high spatial resolution time-series airborne remote sensing. Limnol. Oceanogr. 2008, 53, 2391–2406. [Google Scholar] [CrossRef]
- Schalles, J.F.; Gitelson, A.A.; Yacobi, Y.Z.; Kroenke, A.E. Estimation of Chlorophyll a from Time Series Measurements of High Spectral Resolution Reflectance in an Eutrophic Lake. J. Phycol. 1998, 34, 383–390. [Google Scholar] [CrossRef]
- Gitelson, A.; Mayo, M.; Yacobi, Y.Z.; Parparov, A.; Berman, T. The use of high-spectral-resolution radiometer data for detection of low chlorophyll concentrations in Lake Kinneret. J. Plankton Res. 1994, 16, 993–1002. [Google Scholar] [CrossRef]
- Mayo, M.; Gitelson, A.; Yacobi, Y.Z.; Ben-Avraham, Z. Chlorophyll distribution in Lake Kinneret determined from Landsat Thematic Mapper data. Int. J. Remote Sens. 1995, 16, 175–182. [Google Scholar] [CrossRef]
- Han, L.; Jordan, K.J. Estimating and mapping chlorophyll- a concentration in Pensacola Bay, Florida using Landsat ETM+ data. Int. J. Remote Sens. 2005, 26, 5245–5254. [Google Scholar] [CrossRef]
- Jiao, H.B.; Zha, Y.; Gao, J.; Li, Y.M.; Wei, Y.C.; Huang, J.Z. Estimation of chlorophyll- a concentration in Lake Tai, China using in situ hyperspectral data. Int. J. Remote Sens. 2006, 27, 4267–4276. [Google Scholar] [CrossRef]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Zhang, Y.; Zhang, B. Remote-sensing assessment of regional inland lake water clarity in northeast China. Limnology 2009, 10, 135–141. [Google Scholar] [CrossRef]
- Bowers, D.G.; Harker, G.E.L.; Smith, P.S.D.; Tett, P. Optical properties of a region of freshwater influence (the Clyde Sea). Estuar. Coast. Shelf Sci. 2000, 50, 717–726. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L. Bio-optical properties in waters influenced by the Mississippi River during low flow conditions. Remote Sens. Environ. 2003, 84, 538–549. [Google Scholar] [CrossRef]
- Griffin, C.G.; Frey, K.E.; Rogan, J.; Holmes, R.M. Spatial and interannual variability of dissolved organic matter in the Kolyma River, East Siberia, observed using satellite imagery. J. Geophys. Res. 2011, 116, G03018. [Google Scholar] [CrossRef] [Green Version]
- Kowalczuk, P.; Olszewski, J.; Darecki, M.; Kaczmarek, S. Empirical relationships between coloured dissolved organic matter (CDOM) absorption and apparent optical properties in Baltic Sea waters. Int. J. Remote Sens. 2005, 26, 345–370. [Google Scholar] [CrossRef]










| Parameter | No. of Stations | Mean | Median | Range | Skewness |
|---|---|---|---|---|---|
| Chl-a 1 | 415 | 19.0 | 13.6 | 0.5–215.2 | 4.3 |
| TSM 2 | 415 | 7.6 | 5.7 | 0.6–46.0 | 1.9 |
| aCDOM(442) 3 | 415 | 3.9 | 2.0 | 0.4–43.7 | 4.1 |
| Secchi depth, m | 411 | 1.8 | 1.4 | 0.2–12.2 | 2.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uudeberg, K.; Aavaste, A.; Kõks, K.-L.; Ansper, A.; Uusõue, M.; Kangro, K.; Ansko, I.; Ligi, M.; Toming, K.; Reinart, A. Optical Water Type Guided Approach to Estimate Optical Water Quality Parameters. Remote Sens. 2020, 12, 931. https://doi.org/10.3390/rs12060931
Uudeberg K, Aavaste A, Kõks K-L, Ansper A, Uusõue M, Kangro K, Ansko I, Ligi M, Toming K, Reinart A. Optical Water Type Guided Approach to Estimate Optical Water Quality Parameters. Remote Sensing. 2020; 12(6):931. https://doi.org/10.3390/rs12060931
Chicago/Turabian StyleUudeberg, Kristi, Age Aavaste, Kerttu-Liis Kõks, Ave Ansper, Mirjam Uusõue, Kersti Kangro, Ilmar Ansko, Martin Ligi, Kaire Toming, and Anu Reinart. 2020. "Optical Water Type Guided Approach to Estimate Optical Water Quality Parameters" Remote Sensing 12, no. 6: 931. https://doi.org/10.3390/rs12060931
APA StyleUudeberg, K., Aavaste, A., Kõks, K. -L., Ansper, A., Uusõue, M., Kangro, K., Ansko, I., Ligi, M., Toming, K., & Reinart, A. (2020). Optical Water Type Guided Approach to Estimate Optical Water Quality Parameters. Remote Sensing, 12(6), 931. https://doi.org/10.3390/rs12060931