Intertidal Bathymetry Extraction with Multispectral Images: A Logistic Regression Approach
Abstract
:1. Introduction
2. Study Area and Data Set
2.1. Study Areas
2.2. Satellite Images
2.3. Tide Data
2.4. In Situ Data for Validation
3. Methods
3.1. Preprocessing
3.2. Intertidal Zone Pixels’ Selection
3.3. Logistic Regression
3.4. Derivation of the Bathymetric Model
3.5. Log-Transformed Ratio Bands Bathymetric Models
4. Results
4.1. Pre-Processing
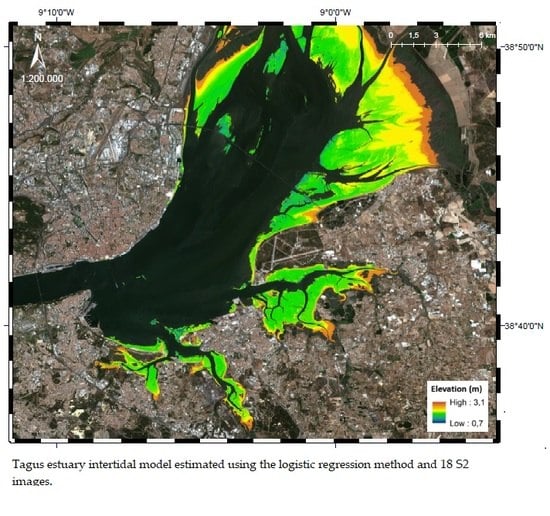
4.2. Intertidal Model Estimation
4.3. Logarithm Ratio Model Estimation
4.4. Validation of the Models
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A



References
- Brito, A.C.; Moita, T.; Gameiro, C.; Silva, T.; Anselmo, T.; Brotas, V. Changes in the Phytoplankton Composition in a Temperate Estuarine System (1960 to 2010). Estuar. Coasts 2015, 38, 1678–1691. [Google Scholar] [CrossRef]
- Taborda, R.; Freire, P.; Silva, A.; Andrade, C.; Freitas, M.C. Origin and evolution of Tagus estuarine beaches. J. Coast. Res. 2009, 56, 213–217. [Google Scholar]
- Gameiro, C.; Cartaxana, P.; Brotas, V. Environmental drivers of phytoplankton distribution and composition in Tagus Estuary, Portugal. Estuar. Coast. Shelf Sci. 2007, 75, 21–34. [Google Scholar] [CrossRef]
- Wright, L.D.; Syvitski, J.P.; Nichols, C.R. Chapter 5: Coastal Morphodynamics and Ecosystem Dynamics. In Tomorrow’s Coasts: Complex and Impermanent; Wright, L.D., Nichols, C.R., Eds.; Springer: New York, NY, USA, 2019; pp. 69–84. [Google Scholar] [CrossRef]
- Guerreiro, M.; Fortunato, A.B.; Freira, P.; Rilo, A.; Taborda, R.; Freitas, A.C.; Andrade, C.; Silva, T.A.; Rodrigues, M.; Bertin, X.A.; et al. Evolution of the hydrodynamics of the Tagus estuary (Portugal) in the 21st century. J. Integr. Coast. Zone Manag. 2015, 15, 65–80. [Google Scholar] [CrossRef]
- Silva, A.N.; Taborda, R.; Antunes, C.; Catalão, J. Understanding the coastal variability at Norte beach, Portugal. J. Coast. Res. 2013, 65, 2173–2178. [Google Scholar] [CrossRef]
- Nerem, R.S.; Beckley, B.D.; Fasulto, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-change–driven accelerated sea-level rise detected in the altimeter era. In Proceedings of the National Academy of Sciences, Toulouse, France, 25 February 2018; pp. 2022–2025. [Google Scholar] [CrossRef] [Green Version]
- Schuerch, M.; Spencer, T.; Temmerman, S.; Kirwan, M.L.; Wolff, C.; Lincke, D.; McOwen, C.J.; Pickering, M.D.; Reef, R.; Vafeidis, A.T.; et al. Future response of global coastal wetlands to sea-level rise. Nature 2018, 561, 231–234. [Google Scholar] [CrossRef]
- Bastos, A.P.; Ponte Lira, C.; Calvão, J.; Catalão, J.; Andrade, C.; Pereira, A.J.; Taborda, R.; Rato, D.; Pinho, P.; Correia, O. UAV Derived Information Applied to the Morphological Study of Slow changing Dune Systems. J. Coast. Res. 2018, 85, 226–230. [Google Scholar] [CrossRef]
- Silva, A.; Taborda, R.; Catalão, J.; Freire, P. DTM extraction using video monitoring techniques: Application to a fetch limited beach. J. Coast. Res. 2009, 56, 203–207. [Google Scholar]
- Bird, C.O.; Bell, P.S.; Plater, A.J. Application of marine radar to monitoring seasonal and event-based changes in intertidal morphology. Geomorphology 2017, 285, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Chénier, R.; Faucher, M.; Ahola, R. Satellite-Derived Bathymetry for Improving Canadian Hydrographic Service Charts. ISPRS Int. J. Geo. Inf. 2018, 7, 306. [Google Scholar] [CrossRef] [Green Version]
- Dierssen, H.M.; Theberge, J.A.E. Bathymetry: Assessing Methods. Volume II Water and Air. Encyc. Nat. Res. 2014. [Google Scholar] [CrossRef]
- Quadros, N.D.; Collier, P.A. A New Approach to Delineating the Littoral Zone for an Australian Marine Cadastre. J. Coast. Res. 2008, 24, 780–789. [Google Scholar] [CrossRef]
- Wozencraft, J.; Millar, D. Airborne Lidar and integrated technologies for coastal mapping and nautical charting. Mar. Techno. Soc. J. 2005, 39, 27–35. [Google Scholar] [CrossRef]
- Jawak, S.D.; Vadlamani, S.S.; Luis, A.J. A Synoptic review on deriving bathymetry information using Remote Sensing Technologies: Models and Comparisons. Adv. Remote Sens. 2015, 4, 147–162. [Google Scholar] [CrossRef] [Green Version]
- Chénier, R.; Ahola, R.; Sagram, M.; Faucher, M.; Shelat, Y. Consideration of Level of Confidence within Multi-Approach Satellite-Derived Bathymetry. ISPRS Int. J. Geo-Inf. 2019, 8, 48. [Google Scholar] [CrossRef]
- Mason, D.C.; Davenport, I. Accurate and Efficient Determination of the Shoreline in ERS-1 SAR images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1243–1253. [Google Scholar] [CrossRef]
- Catalão, J.; Nico, G. Multitemporal backscattering logistic analysis for intertidal bathymetry. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1066–1073. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, Ó. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Niedermeier, A.; Hoja, D.; Lehner, S. Topography and morphodynamics in the German Bight using SAR and optical remote sensing data. Ocean Dyn. 2005, 55, 100–109. [Google Scholar] [CrossRef]
- Schwäbisch, M.; Lehner, S.; Norbert, W. Coastline extraction using ERS SAR interferometry. In Proceedings of the 3rd ERS Symposium, Florence, Italy, 14–21 March 1997; pp. 1049–1053, Space Service Environment, ESA SP-414. [Google Scholar]
- Sagar, S.; Roberts, D.; Bala, B.; Lymburner, L. Extracting the intertidal extent and topography of the Australian coastline from a 28-year time series of Landsat observations. Remote Sens. Environ. 2017, 195, 153–169. [Google Scholar] [CrossRef]
- Bishop, -T.R.; Sagar, S.; Lymburner, L.; Beaman, R. Between the tides: Modelling the elevation of Australia’s exposed intertidal zone at continental scale. Estuar. Coast. Shelf Sci. 2019, 223, 115–128. [Google Scholar] [CrossRef]
- Pahlevan, N.; Sarkar, S.; Franz, B.A.; Balasubramanian, S.V.; He, J. Sentinel-2 MultiSpectral Instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
- Said, R.; Mahmud, M.R.; Hasan, R.C. Evaluating satellite-derived bathymetry accuracy from Sentinel-2A high-resolution multispectral imageries for shallow water hydrographic mapping. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/169/1/012069/pdf (accessed on 24 April 2019).
- Lyzenga, D. Passive Remote-Sensing techniques for mapping water depth and bottom features. App. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined lidar and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral Bathymetry using a Simple Physically Based Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Bell, P.S.; Bird, C.O.; Plater, A.J. A temporal waterline approach to mapping intertidal areas using X-band marine radar. Coast. Engin. 2016, 107, 84–101. [Google Scholar] [CrossRef] [Green Version]
- Instituto Hidrográfico. Tabelas de Marés; Vol II Países Africanos de Língua Oficial Portuguesa e Macau; Instituto Hidrográfico: Lisbon, Portugal, 2018. [Google Scholar]
- Liu, Y.; Li, M.; Zhou, M.; Yang, K.; Mao, L. Quantitative Analysis of the Waterline method for Topographical Mapping of Tidal Flats: A case study in the Dongsha Sandbank, China. Remote Sens. 2013, 5, 6138–6158. [Google Scholar] [CrossRef] [Green Version]
- Ryu, J.-H.; Won, J.S.; Min, K.D. Waterline extraction from Landsat TM data in a tidal flat. A case study in Gomso Bay, Korea. Remote Sens. Environ. 2002, 83, 442–456. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Kim, C.-H.; Lee, Y.-K.; Won, J.-S.; Chun, S.-S.; Lee, S. Detecting the intertidal morphologic change using satellite data. Estuar. Coast. Shelf Sci. 2008, 78, 623–632. [Google Scholar] [CrossRef]
- Neves, F. Dynamics and Hydrology of the TAGUS Estuary: Results from in Situ Observations. Ph.D. Thesis, Faculdade de Ciências da Universidade de Lisboa, Lisbon, Portugal, 2010. [Google Scholar]
- GUINÉ-BISSAU. A Reserva de Biosfera do Arquipélago dos Bijagós: Um Património a Preserver; Ministerio de Agricultura, Alimentación y Medio Ambiente de España, Administração da Guiné-Bissau: Bissau, Guiné-Bissau, 2012; p. 211. [Google Scholar]
- Carvalho, L.; Figueira, P.; Monteiro, R.; Reis, A.; Almeida, J.; Catry, T.; Lourenço, P.; Catry, P.; Barbosa, C.; Catry, I.; et al. Major, minor, trace and rare earth elements in sediments of the Bijagós archipelago, Guinea-Bissau. Mar. Pollut. Bull. 2018, 829–834. [Google Scholar] [CrossRef]
- Sentinel’s Scientific Data Hub. Available online: https://scihub.copernicus.eu/ (accessed on 8 March 2019).
- European Space Agency. Sentinel-2 User Handbook; ESA Standard Document; ESA: Paris, France, 2015; Available online: https://sentinel.esa.int/documents/247904/685211/Sentinel-2_User_Handbook (accessed on 12 June 2019).
- European Space Agency. Sentinel-2 MSI Technical Guide. 2017. Available online: https://earth.esa.int/web/sentinel/technical-guides/sentinel-2-msi (accessed on 18 June 2019).
- Casal, G.; Monteys, X.; Hedley, J.; Harris, P.; Cahalane, C.; McCarthy, T. Assessment of empirical algorithms for bathymetry extraction using Sentinel-2 data. Int. J. Remote Sens. 2019, 40, 2855–2879. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Towards routine mapping shallow bathymetry in environments with variable turbidity: Contribution of Sentinel-2A/B satellites mission. Remote Sens. 2020, 12, 451. [Google Scholar] [CrossRef] [Green Version]
- Vanhellemont, Q.; Ruddick, K. Atmospheric correction of metre-scale optical satellite data for inland and coastal water applications. Remote Sens. Environ. 2018, 216, 586–597. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.; Barrilero, O.; Laporte, J.; Koetzh, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Royal Belgium Institute of Natural Sciences. ACOLITE Python User Manual. 2019. Available online: https://odnature.naturalsciences.be/remsem/software-and-data/acolite (accessed on 27 January 2020).
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef] [Green Version]
- Vanhellemont, Q.; Ruddick, K. Advantages of high quality SWIR bands for ocean colour processing: Examples from Landsat-8. Remote Sens. Environ. 2015, 161, 89–106. [Google Scholar] [CrossRef] [Green Version]
- Vanhellemont, Q.; Ruddick, K. Acolite for Sentinel-2: Aquatic Applications of MSI Imagery. In Proceedings of the ESA Living Planet Symposium, Prague, Chez Republic, 9–13 May 2016. [Google Scholar]
- Ruddick, K.; Vanhellemont, Q.; Dogliotti, A.; Nechad, B.; Pringle, N.; Van der Zande, D. New Opportunities and Challenges for High Resolution Remote Sensing of Water Colour. In Proceedings of the Ocean Optics XXIII, Victoria, BC, Canada, 7 October 2016. [Google Scholar]
- Caballero, I.; Stump, P.R.; Meredith, A. Preliminary assessment of turbidity and chlorophyll impact on bathymetry derived from Sentinel-2A and Sentinel-3A satellites in South Florida. Remote Sens. 2019, 11, 645. [Google Scholar] [CrossRef] [Green Version]
- Caballero, I.; Stumpf, R.P. Retrieval of nearshore bathymetry from Sentinel-2A and 2B satellites in South Florida coastal waters. Estuar. Coast. Shelf Sci. 2019, 226, 106277. [Google Scholar] [CrossRef]
- Instituto Hidrográfico. Levantamento Hidrográfico Instalações Navais da Azinheira (Estuário do Tejo); Instituto Hidrográfico: Lisbon, Portugal, 2018. [Google Scholar]
- Instituto Hidrográfico. Cartas Náuticas do Arquipélago dos Bijagós Guiné-Bissau (223); Instituto Hidrográfico: Lisbon, Portugal, 1969. [Google Scholar]
- International Hydrographic Organization. IHO C-55 Publication Status of Hydrographic Surveying and Charting Worldwide, 2020, Monaco. Available online: https://iho.int/uploads/user/pubs/cb/c-55/c55.pdf (accessed on 17 February 2020).
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, A.A.; Lawrence, R.L. Spectrally based remote sensing of river bathymetry. Earth Surf. Proc. Landf. 2009, 1787. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Vitti, A.; Lyzenga, D. Multiple Optimal Depth Predictors Analysis (MODPA) for river bathymetry: Findings from spectro radiometry, simulations, and satellite imagery. Remote Sens. Environ. 2018, 218, 132–147. [Google Scholar] [CrossRef]
- Hamylton, S.M.; Hedley, J.D.; Beaman, R.J. Derivation of high-resolution bathymetry from multispectral satellite imagery: A comparison of empirical and optimization methods through geographical error analysis. Remote Sens. 2015, 7, 16257–16273. [Google Scholar] [CrossRef] [Green Version]
- Hedley, J.D.; Harborne, A.R.; Mumby, P.J. Simple and robust removal of sun glint for mapping shallow-water benthos. Int. J. Environ. 2005, 113, 2107–2112. [Google Scholar] [CrossRef]
- Mason, D.C.; Davenport, I.J.; Flather, R.A.; Gurney, C.; Robinson, G.J.; Smith, J.A. A sensitivity analysis of the waterline method of constructing a digital elevation model for intertidal areas in ERS SAR scene of eastern England. Estuar. Coast. Shelf Sci. 2001, 53, 759–778. [Google Scholar] [CrossRef]
- Bué, I.; Catalão, J.; Semedo, A. Intertidal Topo-bathymetry extraction from SAR and Multispectral images. In Proceedings of the Living Planet Symposium, Milan, Italy, 13–17 May 2019. [Google Scholar]











| Number | Date | Sensor | Tide Height (m) |
|---|---|---|---|
| (a) | |||
| 1 | 21 March 2018 | S2A | 0.72 |
| 2 | 26 March 2018 | S2B | 2.95 |
| 3 | 05 May 2018 | S2B | 1.40 |
| 4 | 10 May 2018 | S2A | 2.97 |
| 5 | 15 May 2018 | S2B | 1.92 |
| 6 | 19 June 2018 | S2A | 1.68 |
| 7 | 24 June 2018 | S2B | 3.15 |
| 8 | 29 July 2018 | S2A | 1.43 |
| 9 | 03 August 2018 | S2B | 1.58 |
| 10 | 08 August 2018 | S2A | 3.35 |
| 11 | 13 August 2018 | S2B | 0.89 |
| 12 | 18 August 2018 | S2A | 2.19 |
| 13 | 23 August 2018 | S2B | 2.89 |
| 14 | 22 September 2018 | S2B | 2.84 |
| 15 | 27 September 2018 | S2A | 1.17 |
| 16 | 07 October 2018 | S2A | 3.02 |
| 17 | 22 October 2018 | S2B | 2.86 |
| 18 | 27 October 2018 | S2A | 0.99 |
| (b) | |||
| 1 | 01 December 2017 | S2A | 2.19 |
| 2 | 06 December 2017 | S2B | 4.08 |
| 3 | 26 December 2017 | S2B | 1.90 |
| 4 | 10 January 2018 | S2A | 1.39 |
| 5 | 15 January 2018 | S2B | 2.90 |
| 6 | 20 January 2018 | S2A | 3.88 |
| 7 | 25 January 2018 | S2B | 1.36 |
| 8 | 30 January 2018 | S2A | 3.07 |
| 9 | 09 February 2018 | S2A | 1.52 |
| 10 | 19 February 2018 | S2A | 3.97 |
| 11 | 01 March 2018 | S2A | 3.68 |
| 12 | 06 March 2018 | S2B | 3.59 |
| 13 | 21 March 2018 | S2A | 4.01 |
| 14 | 31 March 2018 | S2A | 4.04 |
| 15 | 05 April 2018 | S2B | 3.35 |
| 16 | 15 April 2018 | S2B | 3.75 |
| 17 | 25 April 2018 | S2B | 1.34 |
| 18 | 10 May 2018 | S2A | 1.46 |
| 19 | 20 May 2018 | S2A | 4.16 |
| (a) | ||||
| Candidate pixels | Standard Deviation (m) | |||
| Threshold | sat = 0.2 | sat = 0.3 |  | |
| 0.15 | 1130556 | 0.3463 | 0.3456 | 0.3438 |
 | 1029078 | 0.3413 | 0.3407 |  |
| 0.17 | 945951 | 0.3468 | 0.3449 | 0.3436 |
| 0.18 | 873121 | 0.3557 | 0.3536 | 0.3508 |
| (b) | ||||
| Candidate pixels | Standard Deviation (m) | |||
| Threshold | sat = 0.2 |  | sat = 0.4 | |
| 0.10 | 4445416 | 0.7164 | 0.7172 | 0.7179 |
 | 4131866 | 0.7177 |  | 0.7043 |
| 0.12 | 3895423 | 0.7310 | 0.7157 | 0.7066 |
| 0.13 | 3664775 | 0.7153 | 0.7155 | 0.7158 |
| Algorithm | Sentinel 2 (Images) | N | Bias (m) | STD (m) | RMSE (m) | Max (m) | Min (m) |
|---|---|---|---|---|---|---|---|
| Logarithm Ratio | 08AUG18 (3.35 m tide height) | 507 | 1.81 | 1.31 | 2.23 | 3.74 | −6.98 |
| Logistic Regression | 18 images (Table 1a) | 508 | −0.51 | 0.34 | 0.61 | 2.18 | −1.20 |
| Algorithm | Sentinel 2 (Images) | N | Bias (m) | STD (m) | RMSE (m) | Max (m) | Min (m) |
|---|---|---|---|---|---|---|---|
| Logarithm Ratio | 06DEC2017 (4.08 m tide height) | 78 | 4.84 | 1.26 | 5.00 | −2.21 | −7.54 |
| Logistic Regression | 19 images (Table 1b) | 66 | −0.46 | 0.70 | 0.90 | 1.70 | −1.50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bué, I.; Catalão, J.; Semedo, Á. Intertidal Bathymetry Extraction with Multispectral Images: A Logistic Regression Approach. Remote Sens. 2020, 12, 1311. https://doi.org/10.3390/rs12081311
Bué I, Catalão J, Semedo Á. Intertidal Bathymetry Extraction with Multispectral Images: A Logistic Regression Approach. Remote Sensing. 2020; 12(8):1311. https://doi.org/10.3390/rs12081311
Chicago/Turabian StyleBué, Isabel, João Catalão, and Álvaro Semedo. 2020. "Intertidal Bathymetry Extraction with Multispectral Images: A Logistic Regression Approach" Remote Sensing 12, no. 8: 1311. https://doi.org/10.3390/rs12081311
APA StyleBué, I., Catalão, J., & Semedo, Á. (2020). Intertidal Bathymetry Extraction with Multispectral Images: A Logistic Regression Approach. Remote Sensing, 12(8), 1311. https://doi.org/10.3390/rs12081311