On the Choice of the Third-Frequency Galileo Signals in Accelerating PPP Ambiguity Resolution in Case of Receiver Antenna Phase Center Errors
Abstract
:1. Introduction
2. Methods
2.1. Undifferenced Uncombined Triple-Frequency Observation Equations
2.2. Estimation of Satellite Phase Biases
2.3. Triple-Frequency Ambiguity Resolution
3. Data and Models
4. Results
4.1. Characteristics of Different Galileo Signals and Signal Combinations
4.2. Evaluation of Galileo Phase Biases
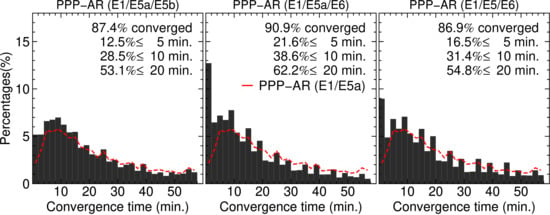
4.3. Results of Triple-Frequency PPP-AR Using the Official GPS Receiver Antenna Corrections
4.4. Results of triple-frequency PPP-AR using the pilot Galileo receiver antenna corrections
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK. GPS Solut. 2015, 19, 151–163. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou + GPS RTK positioning with high cut-off elevation angles. J. Geod. 2014, 88, 335–350. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Lou, Y.; Ye, S.; Zhang, R.; Song, W.; Zhang, X.; Li, Q. Assessment of PPP integer ambiguity resolution using GPS, GLONASS and BeiDou (IGSO, MEO) constellations. GPS Solut. 2017, 21, 1647–1659. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Chang, H.; Li, X. Toward global instantaneous decimeter-level positioning using tightly coupled multi-constellation and multi-frequency GNSS. J. Geod. 2019, 93, 977–991. [Google Scholar] [CrossRef] [Green Version]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the ION GNSS 2005 18th International Technical Meeting of the Satellite Division, Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
- Geng, J.; Meng, X.; Dodson, A.H.; Ge, M.; Teferle, F.N. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning. J. Geod. 2010, 84, 705–714. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Shi, C. Rapid initialization of real-time PPP by resolving undifferenced GPS and GLONASS ambiguities simultaneously. J. Geod. 2017, 91, 361–374. [Google Scholar] [CrossRef]
- Feng, Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals. J. Geod. 2008, 82, 847–862. [Google Scholar] [CrossRef]
- Vollath, U.; Birnbach, S.; Landau, L.; Fraile-ordonez, J.M.; Marti-neira, M. Analysis of three-carrier ambiguity resolution (TCAR) technique for precise relative positioning in GNSS-2. In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998; pp. 417–426. [Google Scholar]
- Hatch, R. A new three-frequency, geometry-free technique for ambiguity resolution. In Proceedings of the ION GNSS 2006, Fort Worth, TX, USA, 26–29 September 2006; pp. 309–316. [Google Scholar]
- Li, P.; Zhang, X.; Ge, M.; Schuh, H. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables. J. Geod. 2018. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Bock, Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution. J. Geod. 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Geng, J.; Guo, J.; Meng, X.; Gao, K. Speeding up PPP ambiguity resolution using triple-frequency GPS/BeiDou/Galileo/QZSS data. J. Geod. 2020. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Li, J.; Zhang, S.; Kuang, K.; Gao, K.; Zhao, Q.; Hong, H. Uncombined precise point positioning with triple-frequency GNSS signals. Adv. Space Res. 2018. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J.G. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Odijk, D.; Ou, J.; Jiang, Z. Rapid integer ambiguity-fixing in precise point positioning. Chin. J. Geophys. 2012, 55, 2203–2211. (In Chinese) [Google Scholar]
- Guo, J.; Geng, J. GPS satellite clock determination in case of inter-frequency clock biases for triple-frequency precise point positioning. J. Geod. 2018, 92, 1133–1142. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Dong, D.; Bock, Y. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Joosten, P.; Tiberius, C. A comparison of TCAR, CIR and LAMBDA GNSS ambiguity resolution. In Proceedings of the ION GPS 2002, Portland, OR, USA, 24–27 September 2002; pp. 2799–2808. [Google Scholar]
- Geng, J.; Guo, J. Beyond three frequencies: An extendable model for single-epoch decimeter-level point positioning by exploiting Galileo and BeiDou-3 signals. J. Geod. 2020, 94. [Google Scholar] [CrossRef]
- Zaminpardaz, S.; Teunissen, P.J.G. Analysis of Galileo IOV + FOC signals and E5 RTK performance. GPS Solut. 2017, 21, 1855–1870. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contribution to the theory of atmospheric refraction: Refraction corrections in satellite geodesy. Bull. Geod. 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.E.; Tregoning, P.; Schuh, H. The Global Mapping Function (GMF): A new empirical mapping function based on data from numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. An optimality property of the integer least-squares estimator. J. Geod. 1999, 73, 587–593. [Google Scholar] [CrossRef]
- Seepersad, G.; Bisnath, S. Reduction of PPP convergence period through pseudorange multipath and noise mitigation. GPS Solut. 2014, 19, 369–379. [Google Scholar] [CrossRef]
- Wang, K.; Khodabandeh, A.; Teunissen, P.J.G. Five-frequency Galileo long-baseline ambiguity resolution with multipath mitigation. GPS Solut. 2018, 22. [Google Scholar] [CrossRef] [Green Version]
- Tu, R.; Liu, J.; Zhang, R.; Zhang, P.; Huang, X.; Lu, X. RTK model and positioning performance analysis using Galileo four-frequency observations. Adv. Space Res. 2019, 63, 913–926. [Google Scholar] [CrossRef]








| Galileo Signals | L1 | L2 | L3 | |
|---|---|---|---|---|
| E1/E5a/E5b | 16.892 | 113.034 | −128.926 | 172.290 |
| E1/E5a/E6 | 20.969 | 33.910 | −53.879 | 67.027 |
| E1/E5a/E5 | 16.216 | 226.068 | −241.284 | 331.041 |
| E1/E5b/E6 | 22.716 | 55.254 | −76.970 | 97.435 |
| E1/E5b/E5 | 17.567 | −257.852 | 241.284 | 353.574 |
| E1/E5/E6 | 21.808 | 42.580 | −63.387 | 79.414 |
| E5a/E5b/E5 | 2938.889 | 3094.222 | −6032.111 | 7389.022 |
| E5a/E5b/E6 | 440.833 | −663.048 | 223.214 | 826.916 |
| E5a/E5/E6 | 881.667 | −1064.490 | 183.824 | 1394.370 |
| E5b/E5/E6 | −1326.095 | 1064.490 | 262.605 | 1720.648 |
| Items | Strategies |
|---|---|
| Observation | Triple-frequency pseudo-range and carrier phase |
| Frequency combination | Galileo: E1/E5a, E1/E5a/E5b, E1/E5a/E6, E1/E5/E6 |
| Observation rate | 30 s |
| Cut-off elevation angle | 10° |
| Observation weighting | Elevation-dependent weighting strategy 3 mm and 0.3 m for raw carrier phase and pseudo-range, respectively |
| Ionosphere delay | Random-walk parameter with a process noise of |
| Troposphere delay | Saastamoinen model [26]; global mapping function (GMF) [27]; estimated hourly with a process noise of |
| PCO/PCV errors | (a) Use an official IGS antenna file (IGS14_2017.atx) to correct the PCO/PCV errors at the satellite end; at the receiver end, use the corrections of GPS for replacement (b) Use a pilot IGS antenna file including all PCO/PCV corrections for Galileo signals at the satellite and receiver ends |
| Precise products | Use final precise orbit, ERP and multi-GNSS DCB products from CODE; estimate precise satellite clock and phase bias products |
| Signals | Extra-Wide-Lane | Wide-Lane | Narrow-Lane |
|---|---|---|---|
| E1/E5a/E5b | 0.001 | 0.013 | 0.015 |
| E1/E5a/E6 | 0.005 | 0.014 | 0.016 |
| E1/E5/E6 | 0.006 | 0.011 | 0.016 |
| Station Name | PPP-AR E1/E5a | PPP-AR E1/E5a/E5b | PPP-AR E1/E5a/E6 | PPP-AR E1/E5/E6 |
|---|---|---|---|---|
| ALBY | 25.2 | 30.6 (−21.5%) | 39.3(−56.0%) | 36.8 (−45.9%) |
| COEN | 39.5 | 39.6 (−0.3%) | 45.7 (−15.6%) | 45.8 (−15.9%) |
| COOL | 26.1 | 30.6 (−17.3%) | 39.4 (−50.8%) | 38.2 (−46.1%) |
| DARW | 46.4 | 39.8 (14.2%) | 45.2 (2.6%) | 44.1 (5.1%) |
| FROY | 28.9 | 23.2 (19.8%) | 29.1 (−0.6%) | 28.7 (0.6%) |
| HNIS | 30.7 | 30.2 (1.6%) | 36.2 (−18.0%) | 35.1 (−14.3%) |
| MEDO | 29.2 | 25.9 (11.2%) | 31.3 (−7.1%) | 30.4 (−4.2%) |
| MTCV | 21.9 | 18.2 (16.8%) | 27.9 (−27.4%) | 26.0 (−18.6%) |
| NORS | 22.6 | 27.5 (−21.3%) | 37.0 (−63.2%) | 34.3 (−51.5%) |
| PTHL | 23.4 | 20.5 (12.4%) | 26.8 (−14.4%) | 26.0 (−11.1%) |
| THEV | 25.2 | 21.7 (14.1%) | 31.3 (−24.3%) | 29.4 (−16.5%) |
| TMBO | 40.1 | 32.8 (18.3%) | 39.9 (0.7%) | 38.0 (5.2%) |
| TOMP | 25.9 | 23.6 (8.7%) | 29.3 (−13.2%) | 27.6 (−6.5%) |
| WILU | 23.2 | 20.5 (11.6%) | 30.3 (−30.6%) | 29.3 (−26.2%) |
| WMGA | 26.2 | 20.6 (21.6%) | 28.8 (−9.8%) | 28.5 (−8.6%) |
| Mean (15 stations) | 28.9 | 26.7 (7.6%) | 34.0 (−17.6%) | 32.6 (−12.7%) |
| STD (15 stations) | 19.9 | 19.9 | 21.3 | 21.1 |
| Mean (12 stations) | 29.8 | 26.2 (12.1%) | 33.1 (−11.2%) | 31.9 (−7.2%) |
| STD (12 stations) | 19.9 | 19.7 | 21.3 | 21.0 |
| Station Name | PPP-AR E1/E5a | PPP-AR E1/E5a/E5b | PPP-AR E1/E5a/E6 | PPP-AR E1/E5/E6 |
|---|---|---|---|---|
| ALBY | 24.5 | 21.6 (11.6%) | 19.4 (20.8%) | 24.2 (1.3%) |
| COEN | 39.3 | 34.8 (11.4%) | 30.5 (22.5%) | 33.8 (14.0%) |
| COOL | 25.8 | 21.8 (15.6%) | 18.7 (27.4%) | 22.8 (11.9%) |
| DARW | 46.3 | 38.1 (17.7%) | 35.8 (22.7%) | 38.2 (17.6%) |
| FROY | 29.1 | 23.3 (19.7%) | 18.6 (36.1%) | 21.7 (25.2%) |
| HNIS | 29.8 | 25.7 (13.8%) | 22.3 (25.0%) | 27.1 (9.0%) |
| MEDO | 29.2 | 26.4 (9.5%) | 20.2 (30.8%) | 23.9 (18.1%) |
| MTCV | 22.5 | 18.3 (18.3%) | 14.7 (34.4%) | 17.1 (23.9%) |
| NORS | 21.3 | 19.2 (10.2%) | 14.1 (33.8%) | 20.5 (3.9%) |
| PTHL | 23.3 | 20.3 (12.7%) | 17.2 (25.6%) | 20.4 (12.5%) |
| THEV | 25.4 | 20.9 (17.8%) | 16.4 (35.3%) | 20.0 (21.0%) |
| TMBO | 39.9 | 25.4 (36.2%) | 22.2 (44.3%) | 24.7 (38.2%) |
| TOMP | 26.1 | 24.2 (7.5%) | 19.0 (27.1%) | 22.9 (12.5%) |
| WILU | 24.0 | 20.5 (14.7%) | 16.4 (31.7%) | 20.2 (16.0%) |
| WMGA | 26.0 | 20.7 (20.7%) | 17.1 (34.3%) | 20.4 (21.8%) |
| Mean (15 stations) | 28.6 | 24.0 (16.2%) | 19.9 (30.3%) | 23.5 (17.7%) |
| STD (15 stations) | 19.9 | 18.9 | 18.2 | 19.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, S.; Geng, J.; Guo, J.; Meng, X. On the Choice of the Third-Frequency Galileo Signals in Accelerating PPP Ambiguity Resolution in Case of Receiver Antenna Phase Center Errors. Remote Sens. 2020, 12, 1315. https://doi.org/10.3390/rs12081315
Xin S, Geng J, Guo J, Meng X. On the Choice of the Third-Frequency Galileo Signals in Accelerating PPP Ambiguity Resolution in Case of Receiver Antenna Phase Center Errors. Remote Sensing. 2020; 12(8):1315. https://doi.org/10.3390/rs12081315
Chicago/Turabian StyleXin, Shaoming, Jianghui Geng, Jiang Guo, and Xiaolin Meng. 2020. "On the Choice of the Third-Frequency Galileo Signals in Accelerating PPP Ambiguity Resolution in Case of Receiver Antenna Phase Center Errors" Remote Sensing 12, no. 8: 1315. https://doi.org/10.3390/rs12081315
APA StyleXin, S., Geng, J., Guo, J., & Meng, X. (2020). On the Choice of the Third-Frequency Galileo Signals in Accelerating PPP Ambiguity Resolution in Case of Receiver Antenna Phase Center Errors. Remote Sensing, 12(8), 1315. https://doi.org/10.3390/rs12081315