Forest Height Estimation Based on P-Band Pol-InSAR Modeling and Multi-Baseline Inversion
Abstract
:1. Introduction
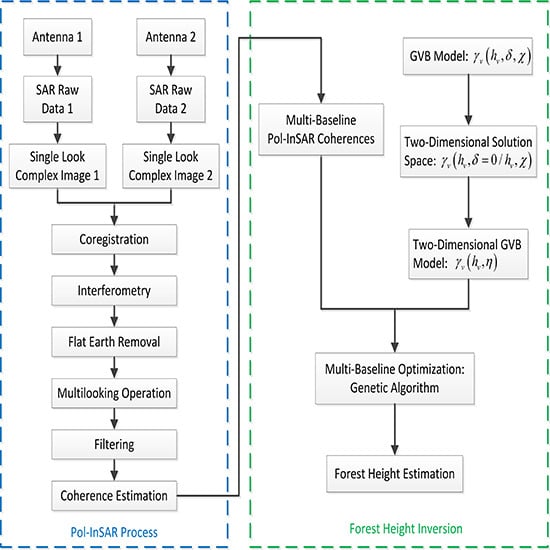
2. Model-Based Pol-InSAR Inversion Theory
2.1. RVoG Model and Inversion
2.2. GVB Model and Inversion
3. Two-Dimensional GVB Model and Inversion
3.1. Two-Dimensional GVB Model
3.2. Pol-InSAR Inversion Based on Two-Dimensional GVB Model
4. Validation with P-Band Pol-InSAR Data
4.1. BIOSAR 2008 Data Introduction
4.2. Experimental Results and Analysis
5. Discussions and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; Van Zyl, J.J. Vegetation characteristics and underlying topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Cloude, S.R. The structure of oriented vegetation from polarimetric interferometry. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2620–2624. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef] [Green Version]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. Proc. Inst. Elect. Eng. Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Cloude, S.R. Robust parameter estimation using dual baseline polarimetric SAR interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 838–840. [Google Scholar]
- Mette, T.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I. Forest and the random volume over ground—Nature and effect of 3 possible error types. In Proceedings of the European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Garestier, F.; Dubois-Fernandez, P.C.; Papathanassiou, K.P. Pine forest height inversion using single-pass X-band PolInSAR data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 59–68. [Google Scholar] [CrossRef]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing performance of L-and P-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens. 2012, 50, 714–726. [Google Scholar] [CrossRef]
- López-Martínez, C.; Alonso-González, A. Assessment and estimation of the RVoG model in polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3091–3106. [Google Scholar] [CrossRef]
- Lei, Y.; Siqueira, P. Estimation of forest height using spaceborne repeat-pass L-band InSAR correlation magnitude over the US state of Maine. Remote Sens. 2014, 6, 10252–10285. [Google Scholar] [CrossRef] [Green Version]
- Ballester-Berman, J.D.; Vicente-Guijalba, F.; Lopez-Sanchez, J.M. A simple RVoG test for PolInSAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1028–1040. [Google Scholar] [CrossRef] [Green Version]
- Kugler, F.; Koudogbo, F.N.; Gutjahr, K.; Papathanassiou, K.P. Frequency effects in Pol-InSAR forest height estimation. In Proceedings of the European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006. [Google Scholar]
- Garestier, F.; Dubois-Fernandez, P.C.; Champion, I. Forest height inversion using high-resolution P-band Pol-InSAR data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3544–3559. [Google Scholar] [CrossRef]
- Kugler, F.; Lee, S.-K.; Papathanassiou, K.P. Estimation of forest vertical structure parameter by means of multi-baseline Pol-InSAR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; pp. IV-721–IV-724. [Google Scholar]
- Garestier, F.; Dubois-Fernandez, P.C.; Guyon, D.; Le Toan, T. Forest biophysical parameter estimation using L- and P-band polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3379–3388. [Google Scholar] [CrossRef]
- Lee, S.-K.; Kugler, F.; Hajnsek, I.; Papathanassiou, K.P. The potential and challenges of polarimetric SAR interferometry techniques for forest parameter estimation at P-band. In Proceedings of the European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 503–505. [Google Scholar]
- Dubois-Fernandez, P.C.; Souyris, J.-C.; Angelliaume, S.; Garestier, F. The compact polarimetry alternative for spaceborne SAR at low frequency. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3208–3222. [Google Scholar] [CrossRef]
- Roueff, A.; Arnaubec, A.; Dubois-Fernandez, P.C.; Refregier, P. Cramer-rao lower bound analysis of vegetation height estimation with random volume over ground model and polarimetric SAR interferometry. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1115–1119. [Google Scholar] [CrossRef]
- Arnaubec, A.; Roueff, A.; Dubois-Fernandez, P.C.; Réfrégier, P. Vegetation height estimation precision with compact PolInSAR and homogeneous random volume over ground model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1879–1891. [Google Scholar] [CrossRef]
- Hajnsek, I.; Scheiber, R.; Keller, M.; Horn, R.; Lee, S.-K.; Ulander, L.; Gustavsson, A.; Sandberg, G.; Le Toan, T.; Tebaldini, S.; et al. BIOSAR 2008: Final Report. 2009. Available online: https://earth.esa.int/c/document_library/get_file?folderId=21020&name=DLFE-903.pdf (accessed on 21 November 2018).
- Fu, H.; Wang, C.; Zhu, J.; Xie, Q.; Zhang, B. Estimation of pine forest height and underlying DEM using multi-baseline P-band PolInSAR data. Remote Sens. 2016, 8, 820. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Wang, B.; Xiang, M.; Jiang, S.; Fu, X. Forest height estimation based on constrained Gaussian vertical backscatter model using multi-baseline P-band Pol-InSAR data. Remote Sens. 2019, 11, 42. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Zhu, J.; Wang, C.; Fu, H.; Lopez-Sanchez, J.M.; Ballester-Berman, J.D. A modified dual-baseline PolInSAR method for forest height estimation. Remote Sens. 2017, 9, 819. [Google Scholar] [CrossRef] [Green Version]
- Garestier, F.; Le Toan, T. Forest modeling for height inversion using single-baseline InSAR/Pol-InSAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1528–1539. [Google Scholar] [CrossRef]
- Garestier, F.; Le Toan, T. Estimation of the backscatter vertical profile of a pine forest using single baseline P-band (Pol-)InSAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3340–3348. [Google Scholar] [CrossRef]
- Hajnsek, I.; Kugler, F.; Lee, S.-K.; Papathanassiou, K.P. Tropical-forest-parameter estimation by means of Pol-InSAR: The INDREX-II campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar] [CrossRef] [Green Version]
- Kugler, F.; Lee, S.-K.; Hajnsek, I.; Papathanassiou, K.P. Forest height estimation by means of Pol-InSAR data inversion: The role of the vertical wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1–R54. [Google Scholar] [CrossRef]
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2880–2888. [Google Scholar] [CrossRef]
- Lavalle, M.; Khun, K. Three-baseline InSAR estimation of forest height. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1737–1741. [Google Scholar] [CrossRef]
- Park, S.-E.; Moon, W.M.; Pottier, E. Assessment of scattering mechanism of polarimetric SAR signal from mountainous forest areas. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4711–4719. [Google Scholar] [CrossRef]
- Lu, H.; Suo, Z.; Guo, R.; Bao, Z. S-RVoG model for forest parameters inversion over underlying topography. Electron. Lett. 2013, 49, 618–620. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, T.; Ding, Z.; Zeng, T.; Long, T. A modified three-stage inversion algorithm based on R-RVoG model for Pol-InSAR data. Remote Sens. 2016, 8, 861. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Wang, B.; Xiang, M.; Fu, X.; Zhou, L.; Li, Y. S-RVoG model inversion based on time-frequency optimization for P-band polarimetric SAR interferometry. Remote Sens. 2019, 11, 1033. [Google Scholar] [CrossRef] [Green Version]
- Tabb, M.; Orrey, J.; Flymn, T.; Carande, R. Phase diversity: A decomposition for vegetation parameter estimation using polarimetric SAR interferometry. In Proceedings of the European Conference on Synthetic Aperture Radar, Cologne, Germany, 4–6 June 2002; pp. 721–724. [Google Scholar]









| Track | Baseline (m) | Range (rad/m) | Range (rad) | Band | Polarization |
|---|---|---|---|---|---|
| Master | Master | Master | 0.44–0.96 | P | Quad |
| Slave | 16 | 0.014–0.135 | Slave | P | Quad |
| Slave | 24 | 0.021–0.181 | Slave | P | Quad |
| Slave | 32 | 0.026–0.245 | Slave | P | Quad |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Wang, B.; Xiang, M.; Zhou, L.; Jiang, S. Forest Height Estimation Based on P-Band Pol-InSAR Modeling and Multi-Baseline Inversion. Remote Sens. 2020, 12, 1319. https://doi.org/10.3390/rs12081319
Sun X, Wang B, Xiang M, Zhou L, Jiang S. Forest Height Estimation Based on P-Band Pol-InSAR Modeling and Multi-Baseline Inversion. Remote Sensing. 2020; 12(8):1319. https://doi.org/10.3390/rs12081319
Chicago/Turabian StyleSun, Xiaofan, Bingnan Wang, Maosheng Xiang, Liangjiang Zhou, and Shuai Jiang. 2020. "Forest Height Estimation Based on P-Band Pol-InSAR Modeling and Multi-Baseline Inversion" Remote Sensing 12, no. 8: 1319. https://doi.org/10.3390/rs12081319
APA StyleSun, X., Wang, B., Xiang, M., Zhou, L., & Jiang, S. (2020). Forest Height Estimation Based on P-Band Pol-InSAR Modeling and Multi-Baseline Inversion. Remote Sensing, 12(8), 1319. https://doi.org/10.3390/rs12081319