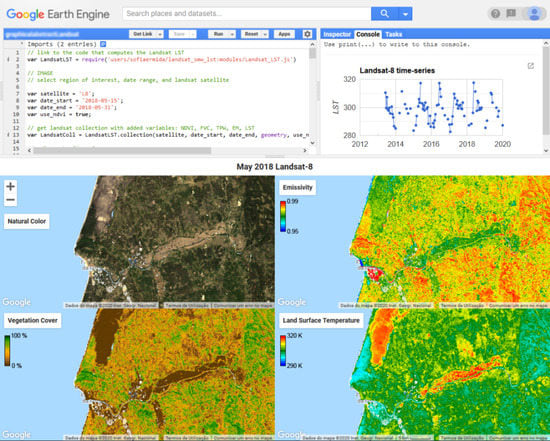
Google Earth Engine Open-Source Code for Land Surface Temperature Estimation from the Landsat Series

Abstract

Land Surface Temperature (LST) is increasingly important for various studies assessing land surface conditions, e.g., studies of urban climate, evapotranspiration, and vegetation stress. The Landsat series of satellites have the potential to provide LST estimates at a high spatial resolution, which is particularly appropriate for local or small-scale studies. Numerous studies have proposed LST retrieval algorithms for the Landsat series, and some datasets are available online. However, those datasets generally require the users to be able to handle large volumes of data. Google Earth Engine (GEE) is an online platform created to allow remote sensing users to easily perform big data analyses without increasing the demand for local computing resources. However, high spatial resolution LST datasets are currently not available in GEE. Here we provide a code repository that allows computing LSTs from Landsat 4, 5, 7, and 8 within GEE. The code may be used freely by users for computing Landsat LST as part of any analysis within GEE.

1. Introduction

Land Surface Temperature (LST) is an important component of the Earth’s energy budget, closely linked to the partitioning between sensible and latent heat fluxes. As such, high-resolution satellite-derived LST is increasingly used in various applications related to the assessment of land surface conditions, including mapping the urban extent and the intensity of urban micro-climates, estimating high-resolution evapotranspiration for the management of water resources and assessing vegetation stress [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15].

The Landsat series of satellites have the potential to provide LST estimates at a high spatial resolution that are particularly appropriate for local and small-scale studies. Numerous LST algorithms for the Landsat series have been proposed [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. While most algorithms are simple to implement, they require users to provide the necessary input data and calibration coefficients, which are generally not readily available. Some datasets are available online (e.g., [25,26]); however, they generally require users to be able to handle large volumes of data. Google Earth Engine (GEE; [31]) is an online platform created to allow remote sensing users to easily perform big data analyses without the need for computation resources. All Landsat Level-1 and 2 data are directly available to GEE, including top-of-atmosphere (TOA) and surface reflectance (SR) data. However, until now high-resolution LST datasets from Landsat have been unavailable in GEE.

High-resolution LST may also be derived from the Chinese Huan Jing 1 (HJ-1) Infrared Scanner (IRS) at about 300 m [32,33] or from the Ecosystem Spaceborne Thermal Radiometer Experiment on Space Station (ECOSTRESS) thermal infrared sensor at about 70 m [34]. While the former is not currently available in GEE, the latter is bounded to provide observations over a relatively short period. The Landsat series, which provides high spatial resolution observations in the thermal infrared (~100 m) available over 38 years, is among the most wide-spread used sensors for high resolution LST retrievals.

Here we propose a methodology for deriving LST from the Landsat series of satellites (i.e., Landsat 4, 5, 7, and 8), which is fully implemented in GEE. Parastatidis et al. [26] previously proposed a similar method that resulted in a web application that allowed users to derive LST data with GEE. However, since the data are only accessible through the web application, this method still requires users to download large amounts of data if they wish to perform time-series analyses. In contrast, here we provide a code repository with all the GEE scripts necessary to compute LSTs from Landsat data. The repository allows users to perform any data analysis they require within GEE without the need to store data locally. The code is written in Javascript and built with the new ‘GEE modules capability’, which makes its application easy—users only need to add a “require(…)” command to their scripts to access the code for computing Landsat LST.

The LST is computed using the Statistical Mono-Window (SMW) algorithm developed by the Climate Monitoring Satellite Application Facility (CM-SAF) for deriving LST climate data records from Meteosat First and Second Generation (MFG and MSG) [35]. Due to its simplicity, the algorithm is easy to calibrate and implement. Besides Landsat data, the LST production code makes use of two other datasets available within GEE, atmospheric data from the re-analyses of the National Center for Environmental Prediction (NCEP) and National Center for Atmospheric Research (NCAR) [36] and surface emissivity from the Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Emissivity Database (ASTER GED) developed by the National Aeronautics and Space Administration’s (NASA) Jet Propulsion Laboratory (JPL) [37].

The quality of the Landsat LST computed with the proposed methodology is assessed with comparisons against in situ LST, which were derived from radiance measurements from six stations belonging to the Surface Radiation Budget Network (SURFRAD) [38], the Baseline Surface Radiation Network (BSRN) [39], and the Karlsruhe Institute of Technology (KIT) network [40].

Section 2 describes the input data used by the LST algorithm (Section 2.1), the LST retrieval procedure (Section 2.2), and the station data used for validation (Section 2.3). Section 3 shows the obtained algorithm calibration (Section 3.1), examples of the derived LST and necessary layers (Section 3.2), and the results of the validation exercises (Section 3.3). Section 4 discusses the results and Section 5 summarizes the presented work.

2. Materials and Methods

2.1. Input Data

2.1.1. Landsat Data

TOA brightness temperatures for the Landsat’s thermal infrared (TIR) channels are provided by the United States Geological Survey (USGS) and are fully available and ready to use in GEE for Landsats 4–8, collection 1. The USGS derives the TOA values from raw orthorectified digital numbers data using the respective calibration coefficients [41]. The data from the Landsat series are considered consistent and inter-calibrated, and all TIR bands have been resampled to 30 m spatial resolution. The data are organized into Tiers based on their quality. Landsat scenes with the highest available data quality are placed into Tier 1, being suitable for time-series analysis, while the remainder are assigned to Tier 2 [42]. The results shown in this work are entirely based on Tier 1 data, but the code may equally be applied to Tier 2 data.

Table 1. Bands, Google Earth Engine dataset, spatial resolution, equatorial crossing time (E.C.T.), and available date range for each Landsat satellite.

Satellite	Used Bands	Wavelength (µm)	Dataset	Spatial Resolution	E.C.T.	Date Range
Landsat 4 (TM)	Red: B3 NIR: B4 TIR: B6	0.63–0.69 0.76–0.90 10.4–12.5	C01/T1_SR C01/T1_SR C01/T1_TOA	30 m 30 m 1202 m	9:45 am (16-day)	22 August 1982 to 14 December 1993
Landsat 5 (TM)	Red: B3 NIR: B4 TIR: B6	0.63–0.69 0.76–0.90 10.4–12.5	C01/T1_SR C01/T1_SR C01/T1_TOA	30 m 30 m 1202 m	9:45 am (16-day)	1 January 1984 to 5 May 2012
Landsat 7 (ETM+)	Red: B3 NIR: B4 TIR: B61	0.63–0.69 0.77–0.90 10.4–12.5	C01/T1_SR C01/T1_SR C01/T1_TOA	30 m 30 m 602 m	10:00 am (16-day)	1 January1999 to present
Landsat 8 (OLI; TIRS)	Red: B4 NIR: B5 TIR: B10	0.64–0.67 0.85–0.88 10.6–11.19	C01/T1_SR C01/T1_SR C01/T1_TOA	30 m 30 m 1002 m	10:00 am (16-day)	11 April 2013 to present

Note: ¹ low gain band (B6_VCID_1); ² resampled to 30 m.

describes the properties of the spectral bands used in this study for each Landsat. Besides the TIR band, the red and near-infrared (NIR) bands are used to derive the Normalized Difference Vegetation Index (NDVI), which is calculated from the SR values (instead of the TOA values, which is less accurate). For Landsat-4 and Landsat-5, data acquisition in the visible and infrared spectral regions is performed by the Thematic Mapper (TM) sensor, while for Landsat 7, it is performed by the Enhanced Thematic Mapper Plus (ETM+; an improved version of the TM). For Landsat 8, the Operational Land Imager (OLI) acquires data in the visible and short-wave infrared range, and the Thermal Infrared Sensor (TIRS) provides the TIR data. The TIR band of Landsat 7 is available in low and high gain variants [43]. Here we choose to use the low-gain version, which has lower radiometric resolution but the higher dynamic range and, therefore, prevents saturation at high brightness temperatures.

The SR data for each Landsat are also available in GEE, as provided by the USGS. The SR data from Landsat 8 are generated using the Land Surface Reflectance Code (LaSRC) algorithm, where atmospheric correction is performed using a radiative transfer model, auxiliary atmospheric data from MODIS, and makes use of the coastal aerosol band for aerosol inversion tests [44]. For Landsat 4-to-7, SRs are derived with the Landsat Ecosystem Disturbance Adaptive Processing System (LEDAPS) algorithm, which calculates the radiative transfer for atmospheric data from MODIS and NCEP.

Cloud coverage information, including cloud shadowing, can be retrieved from the quality assessment band (BQA), which is also made available by the USGS through GEE.

2.1.2. Atmospheric Data

Information on the atmospheric water vapor content is required to better account for atmospheric contributions in the TIR observations. Total Column Water Vapor (TCWV) values from NCEP/NCAR reanalysis data are available on GEE [36]. Currently, the NCEP/NCAR reanalysis is the only global TCWV dataset available on GEE that covers the full period of operations of the Landsat series. The TCWV data are available globally from 1948 to the present, with a six-hourly temporal resolution and 2.5 degrees spatial resolution. TCWV data from the two closest analyses (available at 00, 06, 12, and 18 UTC) are linearly interpolated to each Landsat image acquisition time. Only the NCEP/NCAR grid-boxes containing the respective Landsat pixels are considered.

2.1.3. Surface Emissivity

The LST retrieval algorithm used here requires prescribed values of surface emissivity. As in the operational Landsat LST product [25], we derive the surface emissivity for our LST retrievals from the ASTER GEDv3 dataset developed by JPL [37]. This dataset includes the emissivity for the five ASTER bands in the TIR region and is derived with a Temperature-Emissivity Separation (TES) algorithm from all clear-sky ASTER images acquired between 2000 and 2008. The emissivity data have a reported accuracy of ~0.01 and are provided with a spatial resolution of 100 × 100 m² [45]. The emissivity data are adjusted to match Landsat’s thermal bands using the coefficients provided by [25].

The ASTER GEDv3 dataset corresponds to the average of all retrievals performed over an eight-year period; therefore, emissivity variations over time, e.g., due to annual and inter-annual variations in vegetation density, need to be accounted for. Following [25], we apply a vegetation adjustment using Landsat derived NDVI and mean ASTER GEDv3 NDVI. The NDVI is commonly used to derive the fraction of vegetation cover (FVC) [25,26,37,46]. Here we use the relationship proposed by Carlson and Ripley [46]:

$$FVC={\left(\frac{NDV\mathrm{I}-NDV{I}_{\mathrm{bare}}}{NDV{I}_{\mathrm{veg}}-NDV{I}_{\mathrm{bare}}}\right)}^2$$

(1)

where $NDV{I}_{\mathrm{bare}}$ and $NDV{I}_{\mathrm{veg}}$ are the NDVI values of completely bare and fully vegetated pixels, respectively. Following previous studies (e.g., [17,47,48,49,50]), these two threshold values are set to $NDV{I}_{\mathrm{bare}}=0.2$ and $NDV{I}_{\mathrm{veg}}=0.86$. Although some studies use $NDV{I}_{\mathrm{veg}}=0.5$, Jiménez-Muñoz et al. [50] showed that for high-resolution images, the values between 0.8 and 0.9 are more appropriate. Pixels with NDVI below $NDV{I}_{\mathrm{bare}}$ are considered completely bare, while pixels with NDVI above $NDV{I}_{\mathrm{veg}}$ are considered fully vegetated.

Emissivity values over vegetated areas at any given time, may then be derived using the Vegetation-Cover method [51,52], which is defined as:

$${\epsilon }_b=FVC{\epsilon }_{b,\mathrm{veg}}+\left(1-FVC\right){\epsilon }_{b,\mathrm{bare}}$$

(2)

where ${\epsilon }_{b,\mathrm{veg}}$ and ${\epsilon }_{b,\mathrm{bare}}$ are the emissivity of vegetation and bare ground for a given spectral band b. The emissivity of vegetated surfaces typically shows relatively small variations in the TIR region and, therefore, this value is prescribed to ${\epsilon }_{\mathrm{veg}}=0.99$ [53]. For each pixel, the effective emissivity (${\epsilon }_b$) for each Landsat band is derived as follows [25]:

(1)

ASTER FVC is derived from NDVI using Equation (1);

(2)

The bare ground emissivity (${\epsilon }_{b,\mathrm{bare}}$) for each ASTER band is derived from the original ASTER emissivity (${\epsilon }_b$) and the corresponding ASTER FVC, using Equation (2) with the prescribed value of ${\epsilon }_{b,\mathrm{veg}}=0.99$;

(3)

The bare ground emissivity for each Landsat TIR band (${\epsilon }_{b,\mathrm{bare}}$) is derived from the ASTER bare ground emissivity using the spectral adjustments provided in Table II of [25];

(4)

FVC values for the Landsat image are computed from the respective NDVI values using Equation (1);

(5)

The vegetation cover method (2) is used to obtain the actual surface emissivity for each Landsat TIR band.

For practical purposes, the possibility to directly use the ASTER emissivity corrected for the Landsat TIR band is also available in the code. Users may then choose whether they wish to apply the NDVI-based correction or use the instantaneous ASTER emissivity values.

2.2. LST Retrieval

2.2.1. SMW Algorithm

LST is computed with the SMW algorithm developed and used by CM-SAF to derive LST data records from the MFG and MSG series of satellites. The approach is based on an empirical relationship between TOA brightness temperatures in a single TIR channel and LST and utilizes simple linear regression [35,54,55,56]. The model consists of a linearization of the radiative transfer equation that maintains an explicit dependence on surface emissivity:

$$LST=A_i\frac{Tb}{\epsilon }+B_i\frac{1}{\epsilon }+C_i$$

(3)

where Tb is the TOA brightness temperature in the TIR channel, and $\epsilon$ is the surface emissivity for the same channel. The algorithm coefficients A_i, B_i; and C_i are determined from linear regressions of radiative transfer simulations performed for 10 classes of TCWV (I = 1,…,10), ranging from 0 to 6 cm in steps of 0.6 cm, with values of TCWV above 6 cm being assigned to the last class. Unlike for the analogous algorithms developed by CM-SAF for MFG and MSG, here the coefficients are not stratified by satellite view angle, because the Landsat sensors have a considerably narrower the near-nadir field of view (FOV).

2.2.2. Algorithm Calibration

The calibration database used to obtain the coefficients of Equation (3) has been derived using a dataset of air temperature, water vapor, and ozone profiles compiled by Borbas et al. [57] and its procedure follows Martins et al. [57]. The Borbas dataset comprises over 15,000 profiles and includes ancillary variables such as surface pressure, spectral emissivity, skin temperature, and elevation. To achieve a uniform coverage of surface and atmospheric conditions in the calibration exercise, a sub-set of profiles is selected as follows:

(1)

We define classes of LST ranging from 200 K to 330 K in steps of 5 K, and classes of TCWV from 0 to 6 cm in steps of 0.3 cm. TCWV values above 6 cm are assigned to the last class.

(2)

The Borbas database is iterated to randomly attribute a single clear-sky profile to each TCWV/LST class. At each new iteration, profile selection is limited to those with a great-circle distance to already selected profiles greater than 15 degrees. This guarantees a more extensive geographical coverage of the calibration database.

(3)

For each of the selected profiles, surface conditions are varied to ensure a wide range of conditions are included in the database: following [57], LST is set with respect to air temperature (Tair), namely to the difference between LST and air temperature (LST-Tair) ranging from -15 K to +15 K in steps of 5 K. Surface emissivity values are varied between 0.9 and 0.99 in steps of 0.01.

The selection procedure leads to a set of 257 profiles. For each profile, seven values of LST and 10 values of emissivity are prescribed, which yields a total of 17,990 cases for the calibration exercise, with sample sizes varying between 1260 and 2450 for each TCWV class considered for the coefficient derivation (Section 2.2.1). The obtained coefficients are validated using the full Borbas dataset with the provided LST and emissivity values.

For both, the calibration and validation databases, the respective brightness temperatures that would be observed by the Landsat sensors are computed in the Radiative Transfer for the TIROS Operational Vertical Sounder (RTTOV) version 12 developed by the Numerical Weather Prediction Satellite Application Facility (NWP-SAF) [58].

2.2.3. Processing Chain

Landsat LST values are produced using the algorithm described in Section 2.2.1, with the coefficients determined with the calibration procedure described in Section 2.2.2 and the datasets presented in Section 2.1. The production chain was fully coded in JavaScript using the Code Editor Platform. The code is available from the GEE or Git repositories, respectively:

• https://code.earthengine.google.com/?accept_repo=users/sofiaermida/landsat_smw_lst
• https://earthengine.googlesource.com/users/sofiaermida/landsat_smw_lst

Figure 1 illustrates the processing chain for generating Landsat LSTs. The users first provide the date range, the Landsat satellite (4, 5, 7, or 8), the region of interest to process, and an NDVI flag indicating if they wish to apply the NDVI-based correction to emissivity. Based on this information, the main module, Landsat_LST, loads the respective collections of TOA brightness temperatures (BT) and Surface Reflectance (SR). A cloud mask is applied to both using the quality information bands (module cloudmask). For each TOA BT image, the two closest TCWV NCEP analysis times are selected and interpolated to the Landsat observation time (NCEP_TPW). The SR data are, in turn, used to compute NDVI (compute_NDVI), which is then converted to FVC values as described in Section 2.1.3 (compute_FVC). These FVC values are then used together with previously computed ASTER emissivity values for bare ground (ASTER_bare_emiss) to obtain the corresponding Landsat emissivity (compute_emissivity). Finally, the SMW algorithm is applied to the TOA TB of the Landsat TIR band (SMWalgorithm); the algorithm coefficients are mapped onto the Landsat image based on TWVC from NCEP and taking the classes defined in Section 2.2.1. The code and the LUT containing the coefficients are available to the users in the indicated repository (module SMW_coeffcients).

In the same repository, we provide two scripts with examples demonstrating the usage of the modules for spatial and temporal analysis.

2.3. In situ Data

The quality of the LST data retrieved with the algorithm described above is evaluated by comparing the retrievals with in-situ LST from validation stations. In this study, we use six stations from the SURFRAD network, two stations from the BSRN network, and three stations from the KIT network.

Table 2. Location, land cover type, and start date of the records of the SURFRAD, BSRN, and KIT stations used to assess the quality of the Landsat LST retrievals.

Site Location	ID	Coordinates	Elevation	Land Cover	Start Date
SURFRAD
Bondville, IL	BND	40.051°N 88.373°W	213 m	Grassland	1 April 1994
Desert rock, NV	DRA	36.623 °N 116.020 °W	1004 m	Shrubland	1 March 1998
Fort Peck, MT	FPK	48.308 °N 105.102 °W	636 m	Grassland	1 November 1994
Goodwin Creek, MS	GWN	34.255 °N 89.873 °W	96 m	Grassland	1 December 1994
Penn State Un., PA	PSU	40.720 °N 77.931 °W	373 m	Cropland	1 June 1998
Sioux Falls, SD	SXF	43.734 °N 96.623 °W	483 m	Grassland	1 June 2003
Table Mountain, CO	TBL	40.126 °N 105.238 °W	1692 m	Grassland	1 July 1995
BSRN
Cabauw, Netherlands	CAB	51.9711°N 4.9267°E	0 m	Grassland	1 December 2005
Gobabeb, Namibia	GOB	23.519504°S 15.083229°E	407 m	Desert	15 December 2012
KIT
Evora, Portugal	EVO	38.540 °N 8.003 °W	230 m	Savanna	1 January 2009
Gobabeb, Namibia	GBB	23.551 °S 15.051°E	406 m	Desert	1 January 2009
Kalahari, Namibia	KAL	22.933 °S 17.992 °E	1380 m	Shrubland	1 January 2011

shows the location, land cover type, and period of observation of each station. The SURFRAD network was established in 1993 with the purpose of providing continuous long-term measurements of the surface radiation budget over the United States [38], and their data have been widely used in validation and quality assessment exercises of satellite LST [25,59,60,61,62]. The BSRN is a global network of surface radiation stations managed by the Data and Assessments Panel from the Global Energy and Water Cycle Experiment (GEWEX) under the framework of the World Climate Research Program (WCRP) [39]. From the full BSRN network, we selected two stations that had the necessary variables and were located in sufficiently homogeneous areas. Both the SURFRAD and BSRN stations provide broadband hemispherical upwelling and downwelling infrared radiance measurements performed by pyrgeometers with an uncertainty of about 5 Wm⁻². The KIT stations are specifically dedicated to LST validation [40]. At these stations, Heitronics KT15.85 IIP radiometers (KT15; full-view angle of 8.3°) measure upwelling and downwelling radiances in the 9.6–11.5 μm spectral region, with an accuracy of 0.3 K in equivalent brightness temperature [40]. At the EVO and KAL sites, upwelling radiance is measured by two radiometers, one facing the ground and another a nearby tree. These two measurements allow the upscaling of the upwelling radiances to the satellite FOV [40,63,64].

Station measurements are resampled from the one-minute frequency to satellite observation time by averaging observations performed within ±3 min from the Landsat image acquisition time.

2.3.1. In situ LST Derivation

The pyrogeometers used at SURFRAD and BSRN stations provide broadband radiances in the infrared wavelength range of 4–50 µm. In the case of broadband measurements, the radiative transfer equation may be approximated by the Stefan–Boltzmann law:

$$LST=\sqrt[4]{\frac{L_u-\left(1-{\epsilon }_{BB}\right)L_d}{{\epsilon }_{BB}{\sigma }_{SB}}}$$

(4)

where $L_u$ and $L_d$ are the measured upward and downward longwave radiances, respectively, ${\epsilon }_{BB}$ is the broadband emissivity of the surface, and ${\sigma }_{SB}$ is the Stefan–Boltzmann constant. Following Malakar et al. [25], the broadband emissivity of each site is derived from the ASTER GEDv3 product:

$${\epsilon }_{BB}=0.128+0.014{\epsilon }_{A10}+0.145{\epsilon }_{A11}+0.241{\epsilon }_{A12}+0.467{\epsilon }_{A13}+0.004{\epsilon }_{A14}$$

(5)

where ${\epsilon }_{Ai},j=10-14$ denote the ASTER narrowband emissivities of bands 10 to 14, respectively. To account for vegetation dynamics at the site, each ASTER band emissivity is first corrected using the actual Landsat FVC at the time of observation (see Section 2.1.3). The respective broadband value for each Landsat pixel is then obtained with Equation (5).

For the KIT sites, LST is derived from Planck’s law using a simplified version of the radiative transfer equation [40]:

$$B_{\lambda }\left(\mathrm{LST}\right)=\frac{L_{\lambda ,u}-\left(1-{\epsilon }_{\lambda }\right)L_{\lambda ,d}}{{\epsilon }_{\lambda }}$$

(6)

where $B_{\lambda }\left(\mathrm{LST}\right)$ represents Planck’s function for wavelength $\lambda$, and ${\epsilon }_{\lambda }$ is the respective surface emissivity. $L_{\lambda ,d}$ is the downwelling radiance measured by the upward-facing radiometer. For GBB, the upwelling radiance, $L_{\lambda ,u}$, is directly obtained from the ground-facing radiometer. For EVO and KAL, $L_{\lambda ,u}$ is a simple weighted average of the radiances measured by the ground and tree-facing radiometers, where the fractions of trees/shrubs and ground are used as weights [40,63,64]. To find adequate fractions of trees/shrubs for the Landsat’s FOV, we use high-resolution flight imagery available on GEE. A perimeter of 30 m is defined around the stations, and trees/shrubs are identified manually, yielding values of 45% and 37% for EVO and KAL, respectively. For the GBB station, the emissivity of the site was determined by Goettsche et al. [65], yielding a value of 0.94 for the KT15 radiometer band. For EVO and KAL, in order to account for vegetation dynamics, we use the emissivity values derived for the Landsats, given that the TIR bands are spectrally close to that of the KT15 radiometer. Due to the narrow band of the KT15 radiometers, a central wavelength of 10.55 µm may be considered without significant loss of accuracy [40], and LST is obtained by inverting Plank’s function.

2.3.2. Statistical Metrics

The obtained Landsat LST is assessed using robust statistics, as recommended by the Committee on Earth Observation Satellites Working Group (CEOS) on Calibration and Validation—Land Product Validation (LPV) Subgroup for the validation of Land Surface Temperature Products [66]. The so-called accuracy is given by the median error, which is the robust equivalent to the bias and computed as:

$$\mu =\mathrm{median}\left(LS{T}_{satellite}-LS{T}_{insitu}\right)$$

(7)

where $LS{T}_{satellite}$ and $LS{T}_{insitu}$ are the satellite and in situ LSTs, respectively. The robust equivalent to the error standard deviation is the so-called precision, given by the median of absolute residuals:

$$\sigma =\mathrm{median}\left(\left|\left(LS{T}_{satellite}-LS{T}_{insitu}\right)-\mu \right|\right)$$

(8)

As an estimate of the total uncertainty of the product, we also compute the root mean squared error (RMSE):

$$RMSE=\sqrt{\frac{{\left(LS{T}_{satellite}-LS{T}_{insitu}\right)}^2}{N}}$$

(9)

where N is the sample size.

3. Results

3.1. Algorithm Calibration

Algorithm coefficients (A, B, and C of Equation (3)) are obtained by the ordinary least square fitting against the calibration database described in Section 2.2.2. The database is subdivided in classes of TCWV from 0 to 6 cm in steps of 0.6 cm, yielding a total of 10 sets of (A, B, C) coefficients. Due to the different spectral response functions of the sensors, the calibration must be performed for each Landsat separately. Figure 2 shows the coefficients obtained for the SMW algorithm and Figure 3 shows the LST error distribution of Equation (3) when applied to the validation database. The coefficients determined for the four Landsat sensors are very similar (Figure 2), which is to be expected given their nearly identical TIR bands. As generally seen in LST retrieval algorithms, the retrieval uncertainty increases with TCWV (Figure 3), which is due to the increased atmospheric contribution of the TOA BT. This contribution also impacts the 95% confidence intervals of the coefficients, i.e., they become wider for higher values of TCWV (Figure 2). For Landsat 4 and 7, there is a slight increase of bias with TCWV, with the LST being generally overestimated and biases reaching 0.9 K and 1.4 K, respectively, for very moist atmospheres (Figure 3). For Landsat 5, the increase of the bias with TCWV is particularly high, reaching 2.5 K for TCWV values above 5.4 cm. For Landsat 8, the bias is negligible, and its error dispersion is also lower.

3.2. LST Retrieval

Figure 4 shows an example of some of the layers generated by the LST production chain for each Landsat image; the data were acquired on the 17^th of May 2018 in a region in central Portugal close to Coimbra city, located at approximately 40.2°N and 8.4°W. The region is characterized by extensive forest areas to the west of Coimbra and crop fields in the plains around the banks of the River Mondego. The crop fields are clearly visible in the RGB composite (Figure 4a) in brown tones and correspond mainly to maize, which is generally sown in April and harvested in August or September [67]. In the western part of the Mondego River (close to the river mouth), there are also extensive rice fields. Rice is sown around April/May, and the harvesting takes place around September/October [67]. Close to the seashore, there are also large forest areas, but a larger portion was burned by wildfires in October 2017. The scar of the burned area is also visible in the RGB composite (Figure 4a) as a light brown/yellowish area extending parallel to the coast, from about 40.2°N to 40.4°N.

The first step in the LST production is to match TCVW estimates from NCEP reanalysis data to the Landsat observation time. However, due to the coarse resolution of the model, TCWV values are practically constant over the selected area and, therefore, are not shown. The TIR surface emissivity needed to compute LST is derived from the ASTER GEDv3 dataset. Figure 4b shows the corresponding emissivity map of ASTER band 14, which approximates the Landsat TIR band best. ASTER NDVI values are used to compute the respective FVC, which is shown in Figure 4c. FVC and emissivity values are quite homogeneous over the selected area. FVC is generally quite low, with values between 0.3 and 0.5 for most of the region. The resulting bare ground emissivity map shows values around 0.96–0.97, which matches those typically found in spectral libraries for the 11µm region [53]. Figure 4d shows the respective bare ground emissivity for band 14 derived with Equation (2) from the original emissivity values and the FVC. The FVC values for the Landsat image are also derived from the respective NDVI (Figure 4e). The instantaneous FVC map for Landsat shows considerably more variability than for ASTER. The cropland and burned areas show a clear pattern in the FVC map. Furthermore, the rice fields in the westernmost part of the river had very low NDVI values typically associated with water and, therefore, were masked out. The resulting TIR emissivity values for Landsat are displayed in Figure 4f. Areas with low vegetation density have values close to 0.97, while the emissivity values of densely vegetated areas reach values close to 0.99, both in agreement with typical values in spectral libraries [53]. This example emphasizes the importance of using vegetation cover to derive dynamic emissivity values. Figure 4g shows Landsat TOA brightness temperature values, and Figure 4h the corresponding LST values. For the daytime Landsat scene analyzed here, LST is higher over croplands and burned areas than over forests.

3.3. Validation with in situ LST

The quality of derived Landsat LST is assessed with in situ LST derived from twelve validation stations. Since in situ data were unavailable for Landsat-4, comparisons were only performed for Landsat 5, 7, and 8. We found a considerable number of Landsat LST values, much lower than the in situ estimates, which is probably due to cloud contamination. Besides producing outliers and yielding a bias, cloud contamination also affects NDVI and, therefore, emissivity estimation. Indeed, NDVI values over clouds are generally considerably lower, which results in lower FVC values and, consequently, lower emissivity; however, the dominant effect is the impact on BT. To assess the quality of the satellite LST with a minimum of cloud contamination, we applied a “3σ-Hampel identifier” to remove potential outliers [68,69]. Figure 5 shows scatterplots between Landsat LST and in situ LST for each of the twelve sites. For each Landsat, the 3σ limit is indicated by dashed lines, and the provided statistics are derived after the outliers’ removal.

Table 3. Validation statistics for Landsat 5 (L5), 7 (L7), and 8 (L8) over each site, namely accuracy (µ; K), precision (σ; K), RMSE (K), and the number of observations (N). The black figures are the statistics after removing outliers with the 3σ-rule. The gray figures are the statistics for the original (unfiltered) data.

Station	µ (K)			σ (K)			RMSE (K)			N
	L5	L7	L8	L5	L7	L8	L5	L7	L8	L5	L7	L8
BND	1.2	0.9	1.3	1.4	1.3	1.1	2.5	2.4	2.4	98	177	115
	1.1	0.9	1.1	1.5	1.4	1.3	3.2	3.7	4.3	102	190	133
DRA	0.1	−0.6	−0.4	1.0	0.8	1.0	1.7	1.6	2.0	109	189	201
	0.1	−0.7	−0.6	1.0	1.0	1.2	6.6	4.1	2.9	115	209	215
FPK	1.9	3.0	2.4	1.1	1.8	1.7	2.6	3.9	3.4	110	242	172
	1.8	3.0	2.4	1.4	1.9	1.8	8.8	5.4	3.6	123	250	174
GWN	0.3	0.5	0.0	1.2	0.9	1.1	2.0	1.9	1.8	146	211	115
	0.3	0.5	−0.1	1.2	1.1	1.2	3.4	3.8	2.9	155	227	124
PSU		0.2	0.2		1.0	1.1		1.7	2.0	0	23	22
		0.2	0.2		1.1	1.1		1.9	2.0	0	24	22
SXF	0.6	0.9	1.0	1.1	1.3	1.0	1.7	2.3	2.1	50	100	115
	0.5	0.8	1.4	1.2	1.4	1.2	3.2	3.5	2.6	54	107	123
TBL	2.7	2.6	2.0	1.5	1.9	2.1	3.6	3.7	3.7	119	208	140
	2.5	2.4	1.7	1.7	1.9	2.1	4.5	4.8	5.4	123	219	145
CAB		−1.2	−0.6		0.9	0.9		2.3	1.8	0	46	79
		−1.4	−0.6		1.4	1.1		5.0	3.0	0	56	86
GOB		2.9	2.3		1.6	1.3		3.7	2.9	0	97	131
		3.2	2.4		1.6	1.6		4.2	3.8	0	103	140
EVO	0.3	−1.2	−0.3	1.4	1.3	1.1	2.3	2.2	2.1	29	113	94
	−0.1	−1.2	−0.4	1.3	1.3	1.2	3.7	3.0	3.2	31	119	104
GBB	0.2	0.6	1.3	1.5	1.4	1.0	1.9	2.2	1.9	11	106	102
	0.2	0.6	1.4	1.5	1.5	1.0	1.9	2.4	2.5	11	108	109
KAL		0.1	0.3		1.1	0.8		1.6	1.4	0	70	86
		0.1	0.2		1.2	0.9		2.7	3.7	1	74	92

presents the corresponding statistics for each site (black figures—original data, grey figures—outliers removed).

The accuracy/bias (µ) is generally better than or close to 1 K, except for FPK, TBL, and GOB stations, with values varying between -1.2 and 1.3 K. The bias is highest at the GOB station but it is very low at GBB, which is located in the same area. Apart from FPK, TBL, and GOB, the RMSE values range between 1.4 K and 2.5 K. The lower RMSE values are found in KAL e DRA, and the best precision (σ) values are found in DRA, CAB, and KAL, which are all located in very homogeneous areas. There is no evident pattern when comparing between Landsats; Figure 3 suggests that Landsat 8 might perform slightly better for extremely moist atmospheres (essentially when total column water vapor reaches values above 5 cm), which, outside the tropics, is rare under clear skies. Without considering FPK, TBL, and GOB stations, the overall accuracy of the Landsat 5, 7, and 8 is 0.5 K, 0.0(3) K and 0.3 K, respectively, which meet the threshold accuracy proposed by Guillevic et al. [66]. The overall precision (RMSE) is 1.3 (2.0) K, 1.1 (2.0) K, and 1.0 (1.9) K for Landsat 5, 7, and 8, respectively.

4. Discussion

This work presents a methodology to derive LST from the Landsat series with GEE. We implemented the single-channel empirical algorithm proposed by Duguay-Tetzlaff et al. [35] because it combines simplicity with reasonable accuracy. Furthermore, the CM-SAF used this algorithm to generate a climate data record of LST for the Meteosat series of satellites and, therefore, has been extensively analyzed. A similar algorithm (without explicit dependence on emissivity) is used by the Copernicus Global Land Service to generate LST from the Geostationary Operational Environmental Satellites (GOES) and the Multi-Function Transport Satellite (MTSAT) [55]; a detailed quality assessment of this product is performed continuously and available at https://land.copernicus.eu/global/products/lst. The algorithm uncertainty (Figure 3) obtained here are similar to those obtained by Duguay-Tetzlaff et al. [35] and Freitas et al. [55]. Landsat 5 shows the largest errors, followed by Landsat 7, 4, and 8—these discrepancies are related to the different spectral characteristics of the sensors. While the TIR bands of Landsat 4, 5, and 7 have similar widths, their spectral response functions differ slightly. Of the three satellites, the TIR signal measured by Landsat 5 has the highest weight around 12 µm, followed by Landsat 7 and 4. Since water vapor absorption/emission in the 12 µm spectral region is higher than in the 10–11 µm region, a larger contribution from the 12 µm region decreases the algorithm’s retrieval performance. The TIR band of Landsat 8 is considerably narrower than for the other Landsats, and excludes the 12 µm region, which allows retrieving LST with better accuracy. Algorithms using both TIR bands of Landsat 8 (such as split-window algorithms) could provide better estimates of LST; unfortunately, a calibration problem of the TIRS sensor identified by USGS introduces large calibration uncertainty into the 12 µm band [70]. We confirmed this with independent Landsat 8 LST retrievals with a split-window algorithm, which showed a substantial degradation of retrieval quality over the GBB station (not shown).

The quality of the LST retrievals was further assessed in comparisons with in situ LST estimates from 12 stations obtained from the SURFRAD, BSRN, and KIT networks. The KIT network includes three stations dedicated to LST retrieval located on sites that are homogeneous at the satellite’s pixel scale. At these stations, radiance measurements are performed by radiometers with spectral and directional characteristics similar to those typical of satellite sensors. SURFRAD and BSRN stations provide hemispherical measurements of broadband infrared radiative flux. Despite providing high-quality observations, several authors pointed out several limitations of the SURFRAD measurements for validating satellite LST, most importantly, a lack of spatial representativeness [59,62]. The BSRN sites, CAB and GOB, are located in highly homogeneous areas and have been previously used for validating satellite-derived LST (e.g., [70,71,72]).

In order to study and better understand the impact of land cover heterogeneity on the LST comparisons, we obtained Google high-resolution images for each site (Figure 6). Within GEE, circles with 30 m and 100 m radius were superimposed on the images. The 30 m circle is used to represent the resampled spatial resolution of the Landsat’s TIR bands, while the 100 m circle approximates their original resolution. The 30 m circles correspond to the geometries used in GEE to extract the Landsat LST time-series used in the validation exercise. It should be noted that these geometries are not meant to represent the actual shape of the Landsat pixels. In fact, the actual areas of the circles (with widths of 60 m and 200 m) are larger than both the resampled and original pixel areas. Since the actual position of Landsat pixels varies between overpasses and to account for geolocation uncertainties, we’ve selected a slightly larger area. For some stations, these areas are slightly distanced from the station location in order to encompass more homogeneous surfaces. For instance, at BND shifting the circle slightly to the northeast ensures that most Landsat signal is coming from the grass patch where the station is located (Figure 6a).

4.1. SURFRAD Stations

Statistics at BND, SXF, PSU, and GWN suggest good quality of the LST retrievals and agree well with those obtained by Malakar et al. [25]. Some overestimation at higher LST values is noticeable (above ~305 K; Figure 5). The algorithm validation exercise suggests that the SMW slightly overestimates high LST values for Landsat 5 and 7 and slightly underestimates high LSTs for Landsat 8 (not shown). However, the same bias is not observed at DRA, GBB, or KAL stations where even higher LST values are observed. This suggests a likely underestimation of surface emissivity during the warm season when LSTs are higher. Although the same method is used to obtain Landsat and in situ emissivity, the impact of emissivity uncertainties on LST estimates is different in each case. Empirical LST retrieval algorithms, such as the SMW are generally more sensitive to emissivity errors than methods that derive in situ LST directly with Planck’s or Stefan–Boltzmann law.

Some authors found large biases when validating satellite-derived LST with in situ LST from DRA station (e.g., [25,59,62,73]). In contrast, we found good agreement between Landsat LST and DRA station LST, with bias values within ±0.5 K. DRA station is located in a desert area with sparse shrub cover. This seems to indicate that the station is more representative of Landsat’s spatial scale than satellite sensors with a lower spatial resolution, e.g., MODIS. However, for Landsat, Malakar et al. [25] obtained a large positive bias over DRA. Looking at Figure 13 in Malakar et al. [25], we found that the area we selected for the time-series retrieval is slightly north of the respective area used by Malakar et al. Figure 7 shows LST values from Landsat-8 at DRA averaged for the years 2017 to 2019. The LST values extracted from our selected area (black circle) are on average 1 K lower than the corresponding LST extracted slightly further south (purple circle), which might explain the lower bias.

At the FPK station, the biases are slightly larger (1.3 K, 1.9 K, and 1.8 K for Landsat 5, 7, and 8, respectively) than at most SURFRAD stations (Table 3). The bias seems to be mainly caused by LST observations above 300 K. As mentioned above, this overestimation at high LSTs could be related to an underestimation of emissivity during the warm season. We also obtain large biases at TBL station (2.3 K, 2.1 K, and 1.6 K for Landsat 5, 7, and 8, respectively). Analyses of the average LST retrieved from 2017 to 2019 with Landsat-8 (Figure 7), indicate that there are strong LST variations (almost 10 K) around the station, which are likely due to differences in soil and vegetation. The area selected to extract the Landsat LSTs (black circle) generally has slightly lower LST values than the area directly around the station (purple circle). However, the bias values are still quite high (Table 3), and the high spatial heterogeneity at this small scale makes it difficult to select a single representative area for the station.

4.2. BSRN Stations

The bias obtained at GOB station is quite high (2.3 K and 1.9 K for Landsat 7 and 8, respectively), while at GBB, which is located in the same area, the bias is much lower (0.1 K, -0.1 K, and 1.1 K for Landsat 5, 7, and 8, respectively). At GOB, the downwelling radiance sensor is located near the Gobabeb Research and Training Center, while the upwelling sensor is located approximately 7 km northeast. Since the upwelling radiance is most relevant for LST derivation, we’ve extracted the LST times-series for the Landsat at the location of the upwelling sensor. Nevertheless, the distance between the two sensors may introduce additional uncertainty into the estimation of the in situ LST.

4.3. KIT Stations

Landsat LST shows good agreement with the KIT stations. While EVO and KAL are very homogeneous in terms of land cover, they are heterogeneous when considering the different surface elements. Therefore, a proper upscaling of their in situ LSTs is required [40,63,64]. Given Landsat’s high spatial resolution, we assume that the temperature contrasts between trees/shrubs and sunlit ground are most relevant and neglect possible shadowing effects. This assumption may lead to a slight increase in the in situ LST uncertainty. Also, the upscaling methodology is sensitive to the prescribed fraction of trees/shrubs, particularly at EVO, where LST contrasts between tree crowns and sunlit ground are the highest. Ermida et al. [64] reported that a 5% error in the fraction of tree crown cover could lead to an additional LST uncertainty up to 1.4 K in summer.

The GBB site has been carefully characterized in order to provide very accurate LST estimations for validation exercises. The instrument characteristics are similar to those generally seen in TIR satellite sensors and therefore is likely to provide LST estimates closer to the satellite estimates. Also, the emissivity of the site was obtained experimentally, increasing the accuracy of the in situ LST estimates.

When comparing the three Landsats, we were not able to identify a clear pattern of one sensor outperforming the other. Although we found a slightly poorer algorithm performance for Landsat-7, the general statistics do not indicate a lower LST retrieval quality for this sensor. This may be due to the higher spatial resolution of Landsat 7, which partially compensates the lower radiometric accuracy by reducing problems associated with site heterogeneity. However, when considering only the most homogeneous and stable stations GBB, CAB, and GOB, Landsat-7 LSTs show higher RMSE values that are suspected to be related to limitations in the atmospheric correction. Moreover, the algorithm performance is only slightly reduced for extremely moist atmospheres (Figure 3; TCWV above 5 cm), which rarely occur under clear skies outside the tropics.

It was not possible to validate Landsat-4 LST retrievals since in situ data are unavailable for its period of operation. However, given the nearly identical instrument characteristics of Landsat 4 and 5, we expect the quality of the Landsat-4 LST retrievals to closely resemble that of Landsat-5.

5. Conclusions

High-resolution LST estimates are increasingly used in small-scale studies. The Landsat series of satellites is particularly appropriate for such studies as it provides imagery at a high spatial resolution that is suitable for a broad range of applications. Although various algorithms for deriving Landsat LST have been proposed, such data are not easily available and generally lack consistency for the different Landsat satellites. Furthermore, the existing Landsat LST datasets require users to store the involved data locally, and the data processing and analysis may be computationally demanding. Making use of the computational resources of Google’s servers, the new GEE online platform allows remote sensing data users to easily analyze large amounts of data. This study provides a GEE repository with all the code necessary to derive LST from Landsat. Furthermore, users are not required to download any data: simply by accessing the code, they can perform all their analyses within GEE. Users can also edit the code to better meet their needs, and improvements may be implemented over time. The GEE repository is publicly available at:

https://code.earthengine.google.com/?accept_repo=users/sofiaermida/landsat_smw_lst.

The LST values are estimated using the SMW algorithm developed by CM-SAF. For each Landsat, the algorithm coefficients were derived using the same calibration database, thereby ensuring consistency between the satellites. All inputs to the algorithm are obtained from the GEE catalog, i.e., the water vapor content from NCEP/NCAR reanalysis data and emissivity from the ASTER GEDv3 dataset with an NDVI-based correction for vegetation dynamics. A validation exercise with in situ LST obtained from 12 stations indicated an overall accuracy of 0.5 K, -0.1 K, and 0.2 K and overall RMSE of 2.0 K, 2.1 K, and 2.1 K for Landsat 5, 7, and 8, respectively.

As the code is available publicly, future improvements to this methodology may be implemented based on user feedback.