Evaluating Downscaling Factors of Microwave Satellite Soil Moisture Based on Machine Learning Method
Abstract
:1. Introduction
2. Methods
3. Materials
3.1. Microwave Satellite SM Products
3.2. MODIS Products
3.3. In Situ SM Observation
4. Results
4.1. Evaluation with Original SM
4.2. Evaluation with In Situ SM at CVS
4.3. Evaluation with In Situ SM at Sparse Stations
5. Discussion
5.1. Effects of Different Normalization Methods
5.2. Effects of Different Machine-Learning Methods
5.3. Implications of the Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458, 110–117. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.M.; Melton, F.S.; Teixeira, J.P.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zhao, X.; Chen, Y.; Gong, A.; Yang, J. A new agricultural drought monitoring index combining MODIS NDWI and day–night land surface temperatures: A case study in China. Int. J. Remote Sens. 2013, 34, 8986–9001. [Google Scholar] [CrossRef]
- Pablos, M.; Martínez-Fernández, J.; Sanchez, N.; González-Zamora, Á. Temporal and spatial comparison of agricultural drought indices from moderate resolution satellite soil moisture data over northwest Spain. Remote Sens. 2017, 9, 1168. [Google Scholar] [CrossRef] [Green Version]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res. Atmos. 2007, 112, D11112. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef] [Green Version]
- Gruber, A.; Dorigo, W.; Zwieback, S.; Xaver, A.; Wagner, W. Characterizing coarse-scale representativeness of in situ soil moisture measurements from the international soil moisture network. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Larson, K.M.; Njoku, E.G.; Small, E.E.; et al. State of the art in large-scale soil moisture monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef] [Green Version]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal, and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Das, N.N.; Entekhabi, D.; Njoku, E.G. An algorithm for merging SMAP radiometer and radar data for high-resolution soil-moisture retrieval. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1504–1512. [Google Scholar] [CrossRef]
- Sun, H.; Cai, C.; Liu, H.; Yang, B. Microwave and meteorological fusion: A method of spatial downscaling of remotely sensed soil moisture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1107–1119. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, B.; Liu, H. Spatial evaluation of soil moisture (SM), land surface temperature (LST), and LST-derived SM indexes dynamics during SMAPVEX12. Sensors 2019, 19, 1247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Chauhan, N.S.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Merlin, O.; Walker, J.; Chehbouni, A.; Kerr, Y. Towards deterministic downscaling of SMOS soil moisture using MODIS derived soil evaporative efficiency. Remote Sens. Environ. 2008, 112, 3935–3946. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS soil moisture in Southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Al Bitar, A.; Walker, J.P.; Kerr, Y. An improved algorithm for disaggregating microwave-derived soil moisture based on red, near-infrared and thermal-infrared data. Remote Sens. Environ. 2010, 114, 2305–2316. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Olivera-Guerra, L.; Hssaine, B.A.; Amazirh, A.; Rafi, Z.; Ezzahar, J.; Gentine, P.; Khabba, S.; Gascoin, S.; Er-Raki, S. A phenomenological model of soil evaporative efficiency using surface soil moisture and temperature data. Agric. For. Meteorol. 2018, 501–515. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Hogue, T.S. Improving spatial soil moisture representation through integration of AMSR-E and MODIS products. IEEE Trans. Geosci. Remote Sens. 2012, 50, 446–460. [Google Scholar] [CrossRef]
- Njoku, E.; Wilson, W.; Yueh, S.; Dinardo, S.; Li, F.; Jackson, T.; Lakshmi, V.; Bolten, J. Observations of soil moisture using a passive and active low-frequency microwave airborne sensor during SGP99. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2659–2673. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, B.; Zhang, C.; Liu, H.; Yang, B. DSCALE_mod16: A model for disaggregating microwave satellite soil moisture with land surface evapotranspiration products and gridded meteorological data. Remote Sens. 2020, 12, 980. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Zhan, X.; Miller, S.; Chauhan, N.; Di, L.; Ardanuy, P. Soil Moisture Visible/Infrared Radiometer Suite Algorithm Theoretical Basis Document; Raytheon Syst. Company: Lanham, MD, USA, 2002. [Google Scholar]
- Srivastava, P.K.; Han, D.; Ramirez, M.A.R.; Islam, T. Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, X.; Xiong, W.; He, L.; Lv, F.; Fan, W.; Luo, Z.; Hong, Y. A soil moisture spatial and temporal resolution improving algorithm based on multi-source remote sensing data and GRNN model. Remote Sens. 2020, 12, 455. [Google Scholar] [CrossRef] [Green Version]
- Remesan, R.; Shamim, M.A.; Han, D.; Mathew, J. Runoff prediction using an integrated hybrid modelling scheme. J. Hydrol. 2009, 372, 48–60. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating high-resolution daily soil moisture by using spatial downscaling techniques: A comparison of six machine learning algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Zhang, S.; Wang, J.; Niesel, J. Spatial downscaling of satellite soil moisture data using a vegetation temperature condition index. IEEE Trans. Geosci. Remote Sens. 2016, 54, 558–566. [Google Scholar] [CrossRef]
- Peng, J.; Niesel, J.; Loew, A. Evaluation of soil moisture downscaling using a simple thermal-based proxythe—The REMEDHUS network (Spain) example. Hydrol. Earth Syst. Sci. 2015, 19, 4765–4782. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Miao, F.; Wang, H.; Xu, Z.; Tang, Z.; Yang, L.; Qi, S. Downscaling of satellite remote sensing soil moisture products over the Tibetan Plateau based on the random forest algorithm: Preliminary results. Earth Space Sci. 2020, 7, e2020EA001265. [Google Scholar] [CrossRef]
- Zappa, L.; Forkel, M.; Xaver, A.; Dorigo, W. Deriving field scale soil moisture from satellite observations and ground measurements in a hilly agricultural region. Remote Sens. 2019, 11, 2596. [Google Scholar] [CrossRef] [Green Version]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- SMAP/In Situ Core Validation Site Land Surface Parameters Match-Up Data, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2017. Available online: https://nsidc.org/data/NSIDC-0712/versions/1 (accessed on 1 January 2021).
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T.; et al. SMAP Handbook-Soil Moisture Active Passive: Mapping Soil Moisture and Freeze/Thaw from Space; JPL Publication: Pasadena, CA, USA, 2014.
- Montzka, C.; Bogena, H.; Zreda, M.; Monerris, A.; Morrison, R.; Muddu, S.; Vereecken, H. Validation of spaceborne and modelled surface soil moisture products with cosmic-ray neutron probes. Remote Sens. 2017, 9, 103. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Creating a seamless 1 km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 206, 84–97. [Google Scholar] [CrossRef]
- Shwetha, H.R.; Kumar, D.N. Prediction of high spatio-temporal resolution land surface temperature under cloudy conditions using microwave vegetation index and ANN. ISPRS J. Photogramm. Remote Sens. 2016, 117, 40–55. [Google Scholar] [CrossRef]








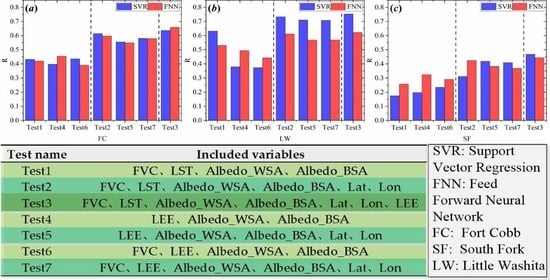
| Test Name | Included Variables |
|---|---|
| Test1 | FVC, LST, Albedo_WSA, Albedo_BSA |
| Test2 | FVC, LST, Albedo_WSA, Albedo_BSA, Lat, Lon |
| Test3 | FVC, LST, Albedo_WSA, Albedo_BSA, Lat, Lon, LEE |
| Test4 | LEE, Albedo_WSA, Albedo_BSA |
| Test5 | LEE, Albedo_WSA, Albedo_BSA, Lat, Lon |
| Test6 | FVC, LEE, Albedo_WSA, Albedo_BSA |
| Test7 | FVC, LEE, Albedo_WSA, Albedo_BSA, Lat, Lon |
| Data | MODIS Product | Unit | Temporal Resolution | Spatial Resolution |
|---|---|---|---|---|
| Albedo | MCD43A3 | N/A | daily | 500 m |
| Land Surface Temperature (LST) | MOD11A1 | Kelvin | daily | 1 km |
| LE | MOD16A2 | J/m²/day | 8-day | 500 m |
| PLE | MOD16A2 | J/m²/day | 8-day | 500 m |
| Leaf area index (LAI) | MOD15A2H | m²/m² | 8-day | 500 m |
| ϑ | MOD09A1 | degree | 8-day | 500 m |
| RMSE (cm3/cm3) | ubRMSE (cm3/cm3) | R | |||||||
|---|---|---|---|---|---|---|---|---|---|
| FC | LW | SF | FC | LW | SF | FC | LW | SF | |
| Test1 | 0.083 | 0.061 | 0.101 | 0.079 | 0.054 | 0.100 | 0.432 | 0.631 | 0.174 |
| Test4 | 0.073 | 0.079 | 0.086 | 0.069 | 0.068 | 0.086 | 0.397 | 0.379 | 0.197 |
| Test6 | 0.077 | 0.073 | 0.090 | 0.070 | 0.068 | 0.089 | 0.435 | 0.373 | 0.234 |
| Test2 | 0.065 | 0.039 | 0.084 | 0.060 | 0.039 | 0.079 | 0.614 | 0.733 | 0.311 |
| Test5 | 0.068 | 0.042 | 0.070 | 0.061 | 0.041 | 0.069 | 0.556 | 0.710 | 0.418 |
| Test7 | 0.064 | 0.043 | 0.072 | 0.056 | 0.042 | 0.071 | 0.580 | 0.708 | 0.409 |
| Test3 | 0.063 | 0.041 | 0.067 | 0.057 | 0.041 | 0.063 | 0.637 | 0.753 | 0.468 |
| RMSE (cm3/cm3) | ubRMSE (cm3/cm3) | R | |||||||
|---|---|---|---|---|---|---|---|---|---|
| COSMOS | SCAN | USCRN | COSMOS | SCAN | USCRN | COSMOS | SCAN | USCRN | |
| Test1 | 0.086 | 0.120 | 0.061 | 0.078 | 0.088 | 0.060 | 0.598 | 0.563 | 0.656 |
| Test4 | 0.082 | 0.120 | 0.073 | 0.075 | 0.086 | 0.068 | 0.490 | 0.629 | 0.457 |
| Test6 | 0.084 | 0.106 | 0.071 | 0.078 | 0.075 | 0.070 | 0.556 | 0.701 | 0.535 |
| Test2 | 0.068 | 0.102 | 0.042 | 0.053 | 0.058 | 0.042 | 0.725 | 0.816 | 0.706 |
| Test5 | 0.073 | 0.114 | 0.042 | 0.059 | 0.068 | 0.040 | 0.672 | 0.774 | 0.728 |
| Test7 | 0.073 | 0.111 | 0.048 | 0.059 | 0.058 | 0.048 | 0.678 | 0.825 | 0.680 |
| Test3 | 0.071 | 0.110 | 0.042 | 0.055 | 0.058 | 0.042 | 0.745 | 0.831 | 0.713 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Cui, Y. Evaluating Downscaling Factors of Microwave Satellite Soil Moisture Based on Machine Learning Method. Remote Sens. 2021, 13, 133. https://doi.org/10.3390/rs13010133
Sun H, Cui Y. Evaluating Downscaling Factors of Microwave Satellite Soil Moisture Based on Machine Learning Method. Remote Sensing. 2021; 13(1):133. https://doi.org/10.3390/rs13010133
Chicago/Turabian StyleSun, Hao, and Yajing Cui. 2021. "Evaluating Downscaling Factors of Microwave Satellite Soil Moisture Based on Machine Learning Method" Remote Sensing 13, no. 1: 133. https://doi.org/10.3390/rs13010133
APA StyleSun, H., & Cui, Y. (2021). Evaluating Downscaling Factors of Microwave Satellite Soil Moisture Based on Machine Learning Method. Remote Sensing, 13(1), 133. https://doi.org/10.3390/rs13010133