Multiscale Adjacent Superpixel-Based Extended Multi-Attribute Profiles Embedded Multiple Kernel Learning Method for Hyperspectral Classification
Abstract
:1. Introduction
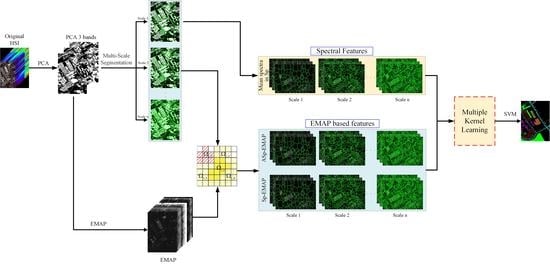
- The superpixel segmentation is used to extract geometric structure information in the HSI, and multiscale spatial information is simultaneously extracted according to the number of superpixels. In addition, the spectral feature of each pixel is replaced by the average of all the spectra in its superpixel, which is used to construct a superpixel-based mean spectral kernel.
- The EMAP features, together with the multiscale superpixels and the adjacent superpixels obtained above, are used to construct the superpixel morphological kernel and the adjacent superpixel morphological kernel. At this stage, multiscale features and multimodal features are fused together to construct three different kernels for classification.
- The multiple kernel learning technique is used to obtain the optimal kernel for HSI classification, which is a linear combination of all the above kernels.
- An experimental evaluation with two well-known datasets illustrates the computational efficiency and quantitative superiority of the proposed MASEMAP-MKL method in terms of all classification accuracies.
2. Materials and Methods
2.1. Preliminary Formulation
2.1.1. Kernelized Support Vector Machine
2.1.2. Superpixel Segmentation
2.1.3. EMAP
2.1.4. CK
- (1)
- Stacked characteristic kernel: In this design, both the spectral and spatial features are directly stacked together as sample features.
- (2)
- Direct addition kernel: The spatial feature after nonlinear mapping is juxtaposed with the spectral feature as the feature of a high-dimensional space.
- (3)
- Weighted summation kernel: By assigning different weights to the spatial and spectral features, is the weight parameter of the balanced spatial and spectral kernel. The weighted summation kernel can be constructed as follows:
2.2. The Proposed MASEMAP-MKL Method
2.2.1. Adjacent Superpixel-Based EMAP Generation
- (1)
- Superpixel-based mean spectral feature:
- (2)
- Superpixel-based morphological feature:
- (3)
- Adjacent superpixel-based morphological feature:
2.2.2. Multiscale Kernel Generation
2.2.3. Multiple Kernel Learning Based on PCA
- (1)
- Construct the three kinds of kernel matrices at scale i using the training samples, i.e., where is the number of all training samples. Therefore, the kernel matrix for the three kinds of features can be calculated by the following formulations.
- (2)
- For the above three types of kernel matrices, we first vectorize them by column to generate kernel feature vectors, then use these vectors as columns to form a matrix D, which is called a multi-scale kernel matrix.
- (3)
- Calculate the singular value decomposition of the covariance matrix of the matrix, that is , and we have the following formula to calculate the weights in Equation (22).
| Algorithm 1 Proposed MASEMAP-MKL for HSI Classification |
|
3. Results
3.1. Datasets’ Description
3.1.1. Indian Pines
3.1.2. University of Pavia
3.2. Comparison Methods and Evaluation Indexes
3.3. Classification Results
3.4. Classification Accuracy
4. Discussion
4.1. Parameter Analysis
4.2. Execution Efficiency
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PCA | principal component analysis |
| EMAP | extended morphological attribute profiles |
| SLIC | simple linear iterative clustering |
| HSI | hyperspectral images |
| SVM | support vector machines |
| CK | composite kernel |
| SSK | spatial-spectral kernel |
| ASMSSK | adjacent superpixel-based multiscale SSK |
| LRCISSSK | low-rank component induced SSK |
| RMK | region-based multiple kernel |
| SpMK | superpixel-based multiple kernel |
| ANSSK | adaptive nonlocal SSK |
| SVM-CK | support vector machine and composite kernel method |
References
- Zhong, S.; Chang, C.; Li, J.; Shang, X.; Chen, S.; Song, M.; Zhang, Y. Class feature weighted hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4728–4745. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Zhao, M.; Song, M.; Wang, Y.; Li, F.; Han, R.; Chang, C. Hyperspectral image classification method based on CNN architecture embedding with hashing semantic feature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1866–1881. [Google Scholar] [CrossRef]
- Acosta, I.C.C.; Khodadadzadeh, M.; Tusa, L.; Ghamisi, P.; Gloaguen, R. A machine learning framework for drill-core mineral mapping using hyperspectral and high-resolution mineralogical data fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4829–4842. [Google Scholar] [CrossRef]
- Cao, Y.; Mei, J.; Wang, Y.; Zhang, L.; Peng, J.; Zhang, B.; Li, L.; Zheng, Y. SLCRF: Subspace learning with conditional random field for hyperspectral image classification. IEEE Trans. Geosci. Remote. Sens. 2020, 1–15. [Google Scholar] [CrossRef]
- Yan, L.; Fan, B.; Liu, H.; Huo, C.; Xiang, S.; Pan, C. Triplet adversarial domain adaptation for pixel-level classification of VHR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3558–3573. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, F.; Long, M. Robust coverless image steganography based on DCT and LDA topic classification. IEEE Trans. Multimed. 2018, 20, 3223–3238. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, W.; Zuo, J.; Yang, K. The fire recognition algorithm using dynamic feature fusion and IV-SVM classifier. Clust. Comput. 2019, 22, 7665–7675. [Google Scholar] [CrossRef]
- Cui, H.; Shen, S.; Gao, W.; Liu, H.; Wang, Z. Efficient and robust large-scale structure-from-motion via track selection and camera prioritization. ISPRS J. Photogramm. Remote Sens. 2019, 156, 202–214. [Google Scholar] [CrossRef]
- Song, Y.; Cao, W.; Shen, Y.; Yang, G. Compressed sensing image reconstruction using intra prediction. Neurocomputing 2015, 151, 1171–1179. [Google Scholar] [CrossRef]
- Sun, L.; He, C.; Zheng, Y.; Tang, S. SLRL4D: Joint restoration of subspace low-rank learning and non-local 4-d transform filtering for hyperspectral image. Remote Sens. 2020, 12, 2979. [Google Scholar] [CrossRef]
- Song, Y.; Yang, G.; Xie, H.; Zhang, D.; Xingming, S. Residual domain dictionary learning for compressed sensing video recovery. Multimed. Tools Appl. 2017, 76, 10083–10096. [Google Scholar] [CrossRef]
- Tu, B.; Huang, S.; Fang, L.; Zhang, G.; Wang, J.; Zheng, B. Hyperspectral image classification via weighted joint nearest neighbor and sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4063–4075. [Google Scholar] [CrossRef]
- Peng, J.; Sun, W.; Du, Q. Self-paced joint sparse representation for the classification of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1183–1194. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral–spatial hyperspectral image classification via multiscale adaptive sparse representation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7738–7749. [Google Scholar] [CrossRef]
- Dundar, T.; Ince, T. Sparse representation-based hyperspectral image classification using multiscale superpixels and guided filter. IEEE Geosci. Remote Sens. Lett. 2019, 16, 246–250. [Google Scholar] [CrossRef]
- Jia, S.; Deng, X.; Zhu, J.; Xu, M.; Zhou, J.; Jia, X. Collaborative representation-based multiscale superpixel fusion for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7770–7784. [Google Scholar] [CrossRef]
- Yang, J.; Qian, J. Hyperspectral image classification via multiscale joint collaborative representation with locally adaptive dictionary. IEEE Geosci. Remote Sens. Lett. 2018, 15, 112–116. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Li, H.; Mei, X.; Ma, J. Hyperspectral image classification with discriminative kernel collaborative representation and tikhonov regularization. IEEE Geosci. Remote Sens. Lett. 2018, 15, 587–591. [Google Scholar] [CrossRef]
- Wang, Q.; He, X.; Li, X. Locality and structure regularized low rank representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 911–923. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Mei, J.; Zhang, L.; Zhang, B.; Li, A.; Zheng, Y.; Zhu, P. Self-supervised low-rank representation (sslrr) for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5658–5672. [Google Scholar] [CrossRef]
- Ding, Y.; Chong, Y.; Pan, S. Sparse and low-rank representation with key connectivity for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5609–5622. [Google Scholar] [CrossRef]
- Mei, S.; Hou, J.; Chen, J.; Chau, L.; Du, Q. Simultaneous spatial and spectral low-rank representation of hyperspectral images for classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2872–2886. [Google Scholar] [CrossRef]
- Wei, W.; Yongbin, J.; Yanhong, L.; Ji, L.; Xin, W.; Tong, Z. An advanced deep residual dense network (DRDN) approach for image super-resolution. Int. J. Comput. Intell. Syst. 2019, 12, 1592–1601. [Google Scholar] [CrossRef] [Green Version]
- Fan, B.; Liu, H.; Zeng, H.; Zhang, J.; Liu, X.; Han, J. Deep unsupervised binary descriptor learning through locality consistency and self distinctiveness. IEEE Trans. Multimed. 2020. [Google Scholar] [CrossRef]
- Zeng, D.; Dai, Y.; Li, F.; Wang, J.; Sangaiah, A.K. Aspect based sentiment analysis by a linguistically regularized CNN with gated mechanism. J. Intell. Fuzzy Syst. 2019, 36, 3971–3980. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, X.; Sun, J.; Wang, J.; Sangaiah, A.K. Spatial and semantic convolutional features for robust visual object tracking. Multimed. Tools Appl. 2020, 79, 15095–15115. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More diverse means better: Multimodal deep learning meets remote-sensing imagery classification. IEEE Trans. Geosci. Remote. Sens. 2020, 1–15. [Google Scholar] [CrossRef]
- Hong, D.; Yokoya, N.; Chanussot, J.; Zhu, X.X. An augmented linear mixing model to address spectral variability for hyperspectral unmixing. IEEE Trans. Image Process. 2018, 28, 1923–1938. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Song, X.; Sun, L.; Huang, W.; Wang, J. A novel cubic convolutional neural network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4133–4148. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, B.; Sun, L.; Zhan, T.; Tang, S. 3-D Channel and spatial attention based multiscale spatial–spectral residual network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4311–4324. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, H.; Eom, K.B. Active deep learning for classification of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 712–724. [Google Scholar] [CrossRef] [Green Version]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Li, J.; Plaza, A. Active learning with convolutional neural networks for hyperspectral image classification using a new bayesian approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6440–6461. [Google Scholar] [CrossRef]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.Y.K.; Zhang, X.; Huang, X. Hyperspectral image classification with deep learning models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised hyperspectral image classification based on generative adversarial networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 212–216. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Xia, R.; Zhang, Q.; Cao, Z.; Yang, K. The visual object tracking algorithm research based on adaptive combination kernel. J. Ambient Intell. Humaniz. Comput. 2019, 10, 4855–4867. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q.; Fan, B.; Wang, Z.; Han, J. Features combined binary descriptor based on voted ring-sampling pattern. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 3675–3687. [Google Scholar] [CrossRef]
- Zhan, T.; Sun, L.; Xu, Y.; Wan, M.; Wu, Z.; Lu, Z.; Yang, G. Hyperspectral classification using an adaptive spectral-spatial kernel-based low-rank approximation. Remote Sens. Lett. 2019, 10, 766–775. [Google Scholar] [CrossRef]
- Gu, Y.; Chanussot, J.; Jia, X.; Benediktsson, J.A. Multiple kernel learning for hyperspectral image classification: A review. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6547–6565. [Google Scholar] [CrossRef]
- Zhan, T.; Sun, L.; Xu, Y.; Yang, G.; Zhang, Y.; Wu, Z. Hyperspectral classification via superpixel kernel learning-based low rank representation. Remote Sens. 2018, 10, 1639. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Zhang, X. Composite kernel classification using spectral-spatial features and abundance information of hyperspectral image. In Proceedings of the 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–5. [Google Scholar]
- Jin, X.; Gu, Y. Combine reflectance with shading component for hyperspectral image classification. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 9–12. [Google Scholar]
- Chen, P. Hyperspectral image classification based on broad learning system with composite feature. In Proceedings of the 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 28–30 July 2020; pp. 842–846. [Google Scholar]
- Chen, Y.; Xiong, J.; Xu, W.; Zuo, J. A novel online incremental and decremental learning algorithm based on variable support vector machine. Clust. Comput. 2019, 22, 7435–7445. [Google Scholar] [CrossRef]
- Huang, H.; Duan, Y.; Shi, G.; Lv, Z. Fusion of weighted mean reconstruction and svmck for hyperspectral image classification. IEEE Access 2018, 6, 15224–15235. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Fusion of multiple edge-preserving operations for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10336–10349. [Google Scholar] [CrossRef]
- Tajiri, K.; Maruyama, T. FPGA acceleration of a supervised learning method for hyperspectral image classification. In Proceedings of the 2018 International Conference on Field-Programmable Technology (FPT), Naha, Japan, 10–14 December 2018; pp. 270–273. [Google Scholar]
- Hong, D.; Yokoya, N.; Ge, N.; Chanussot, J.; Zhu, X.X. Learnable manifold alignment (LeMA): A semi-supervised cross-modality learning framework for land cover and land use classification. ISPRS J. Photogramm. Remote Sens. 2019, 147, 193–205. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Liang, T.; Zhang, Y.; Du, B. Spectral-spatial weighted kernel manifold embedded distribution alignment for remote sensing image classification. IEEE Trans. Cybern. 2020, 1–13. [Google Scholar] [CrossRef]
- Sun, L.; Ma, C.; Chen, Y.; Shim, H.J.; Wu, Z.; Jeon, B. Adjacent superpixel-based multiscale spatial-spectral kernel for hyperspectral classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1905–1919. [Google Scholar] [CrossRef]
- Yang, H.L.; Zhang, Y.; Prasad, S.; Crawford, M. Multiple kernel active learning for robust geo-spatial image analysis. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1218–1221. [Google Scholar]
- Wang, J.; Jiao, L.; Wang, S.; Hou, B.; Liu, F. Adaptive nonlocal spatial–spectral kernel for hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4086–4101. [Google Scholar] [CrossRef]
- Sun, L.; Ma, C.; Chen, Y.; Zheng, Y.; Shim, H.J.; Wu, Z.; Jeon, B. Low rank component induced spatial-spectral kernel method for hyperspectral image classification. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 3829–3842. [Google Scholar] [CrossRef]
- Wang, Q.; Gu, Y.; Tuia, D. Discriminative multiple kernel learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3912–3927. [Google Scholar] [CrossRef]
- Li, F.; Lu, H.; Zhang, P. An innovative multi-kernel learning algorithm for hyperspectral classification. Comput. Electr. Eng. 2019, 79, 106456. [Google Scholar] [CrossRef]
- Li, D.; IEEE, Q.W.M.; Kong, F. Superpixel-feature-based multiple kernel sparse representation for hyperspectral image classification. Signal Process. 2020, 2020, 107682. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; SAsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [Green Version]
- Dalla Mura, M.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of hyperspectral images by using extended morphological attribute profiles and independent component analysis. IEEE Geosci. Remote Sens. Lett. 2011, 8, 542–546. [Google Scholar] [CrossRef] [Green Version]
- Peeters, S.; Marpu, P.R.; Benediktsson, J.A.; Dalla Mura, M. Classification using extended morphological sttribute profiles based on different feature extraction techniques. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Cananda, 24–29 July 2011; pp. 4453–4456. [Google Scholar]
- Song, B.; Li, J.; Li, P.; Plaza, A. Decision fusion based on extended multi-attribute profiles for hyperspectral image classification. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 25–28 June 2013; pp. 1–4. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Calpe-Maravilla, J. Composite kernels for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of hyperspectral images by exploiting spectral–spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.; Wu, X.; Ghamisi, P.; Chanussot, J.; Yokoya, N.; Zhu, X. Invariant attribute profiles: A spatial-frequency joint feature extractor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3791–3808. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wu, Z.; Xiao, Z.; Yang, J. Region-based relaxed multiple kernel collaborative representation for hyperspectral image classification. IEEE Access 2017, 5, 20921–20933. [Google Scholar] [CrossRef]




| Indian Pines | University of Pavia | ||||||
|---|---|---|---|---|---|---|---|
| Class | Name | Train | Test | Class | Name | Train | Test |
| 1 | Alfalfa | 2 | 52 | 1 | Asphalt | 15 | 6626 |
| 2 | Corn-no till | 40 | 1394 | 2 | Meadows | 15 | 18,644 |
| 3 | Corn-min till | 24 | 810 | 3 | Gravel | 15 | 2094 |
| 4 | Corn | 7 | 227 | 4 | Tree | 15 | 3059 |
| 5 | Grass/pasture | 14 | 483 | 5 | Metal sheets | 15 | 1340 |
| 6 | Grass/tree | 24 | 723 | 6 | Bare soil | 15 | 5024 |
| 7 | Grass/pasture-mowed | 2 | 24 | 7 | Bitumen | 15 | 1325 |
| 8 | Hay-windrowed | 13 | 476 | 8 | Bricks | 15 | 3677 |
| 9 | Oats | 2 | 18 | 9 | Shadows | 15 | 942 |
| 10 | Soybeans-no till | 14 | 954 | ||||
| 11 | Soybeans-min till | 70 | 2498 | ||||
| 12 | Soybeans-clean till | 15 | 599 | ||||
| 13 | Wheat | 8 | 204 | ||||
| 14 | Woods | 36 | 1258 | ||||
| 15 | Bldg-grass-tree-drives | 11 | 369 | ||||
| 16 | Stone-steel towers | 4 | 91 | ||||
| Total | 286 | 10,180 | Total | 135 | 42,641 | ||
| Categories | SVMCK [63] | SpMK [64] | ANSSK [54] | RMK [66] | EMAP [60] | AIP [65] | ASMSSK [52] | LRCISSK [55] | MASEMAP-MKL |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 19.01 | 80.00 | 95.58 | 94.81 | 95.97 | 58.65 | 97.12 | 97.12 | 100.00 |
| 2 | 83.15 | 85.60 | 96.15 | 94.89 | 62.59 | 74.41 | 96.78 | 96.61 | 98.64 |
| 3 | 81.44 | 78.52 | 95.35 | 94.23 | 75.12 | 66.67 | 98.62 | 97.10 | 99.26 |
| 4 | 34.63 | 62.82 | 96.87 | 84.41 | 76.75 | 68.90 | 91.06 | 91.94 | 97.80 |
| 5 | 85.26 | 86.50 | 87.83 | 90.66 | 79.41 | 63.02 | 94.62 | 90.43 | 99.79 |
| 6 | 95.99 | 96.46 | 97.01 | 98.66 | 94.34 | 70.08 | 98.46 | 97.43 | 98.06 |
| 7 | 10.00 | 95.83 | 97.08 | 96.25 | 92.31 | 81.25 | 95.42 | 95.83 | 100.00 |
| 8 | 97.50 | 98.36 | 99.47 | 99.24 | 93.20 | 80.29 | 99.79 | 99.90 | 100.00 |
| 9 | 0.00 | 98.89 | 90.56 | 100.00 | 100.00 | 67.78 | 99.44 | 96.67 | 100.00 |
| 10 | 29.43 | 76.31 | 86.97 | 86.80 | 77.70 | 53.12 | 89.42 | 84.65 | 92.14 |
| 11 | 90.34 | 89.87 | 97.68 | 97.77 | 70.86 | 79.13 | 98.72 | 97.75 | 98.04 |
| 12 | 73.81 | 59.18 | 94.99 | 92.39 | 70.89 | 60.67 | 98.18 | 93.32 | 97.50 |
| 13 | 94.80 | 99.31 | 99.22 | 99.51 | 98.03 | 70.05 | 99.02 | 99.36 | 99.02 |
| 14 | 96.48 | 95.93 | 99.72 | 99.63 | 78.76 | 81.02 | 99.22 | 99.49 | 98.73 |
| 15 | 61.95 | 74.09 | 96.12 | 96.48 | 70.15 | 77.67 | 96.26 | 95.18 | 98.65 |
| 16 | 88.02 | 81.10 | 95.38 | 96.26 | 90.71 | 69.34 | 94.84 | 96.15 | 92.31 |
| OA(%) | 80.11 | 85.63 | 95.84 | 95.41 | 75.69 | 72.11 | 97.12 | 95.76 | 97.90 |
| std (%) | 1.54 | 1.13 | 1.07 | 0.89 | 1.67 | 1.33 | 1.05 | 0.68 | 1.02 |
| AA (%) | 63.94 | 84.92 | 95.37 | 95.12 | 82.92 | 70.13 | 96.69 | 95.56 | 98.12 |
| std (%) | 1.94 | 1.59 | 1.70 | 0.89 | 0.54 | 2.34 | 0.99 | 0.85 | 0.96 |
| Kappa | 0.7702 | 0.8357 | 0.9525 | 0.9477 | 0.7256 | 0.6816 | 0.9672 | 0.9517 | 0.9761 |
| std | 0.0187 | 0.0129 | 0.0122 | 0.0102 | 0.0177 | 0.0153 | 0.0120 | 0.0078 | 0.0110 |
| Categories | SVMCK [63] | SpMK [64] | ANSSK [54] | RMK [66] | EMAP [60] | AIP [65] | ASMSSK [52] | LRCISSK [55] | MASEMAP-MKL |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 83.02 | 90.08 | 89.83 | 94.76 | 86.60 | 84.28 | 96.60 | 96.21 | 93.49 |
| 2 | 82.91 | 80.87 | 86.07 | 91.07 | 74.12 | 85.61 | 93.60 | 89.79 | 98.66 |
| 3 | 78.97 | 91.47 | 81.81 | 95.55 | 92.71 | 85.18 | 99.51 | 92.62 | 99.74 |
| 4 | 93.10 | 81.22 | 88.03 | 89.18 | 91.14 | 80.93 | 89.22 | 90.43 | 88.32 |
| 5 | 99.02 | 98.87 | 96.92 | 98.85 | 97.18 | 99.56 | 98.68 | 99.44 | 98.57 |
| 6 | 81.67 | 93.89 | 96.85 | 92.68 | 81.39 | 95.28 | 97.94 | 98.86 | 96.97 |
| 7 | 89.63 | 99.47 | 96.88 | 97.55 | 97.94 | 94.03 | 98.94 | 98.87 | 99.24 |
| 8 | 76.32 | 92.20 | 91.44 | 93.21 | 90.88 | 73.31 | 98.22 | 98.33 | 98.69 |
| 9 | 98.42 | 81.26 | 99.36 | 88.73 | 99.57 | 99.25 | 97.44 | 91.04 | 98.44 |
| OA (%) | 83.80 | 86.49 | 89.28 | 92.49 | 82.49 | 86.12 | 95.36 | 94.62 | 96.99 |
| std (%) | 3.01 | 4.18 | 2.86 | 2.93 | 2.90 | 2.35 | 3.41 | 3.58 | 1.04 |
| AA (%) | 87.01 | 89.92 | 91.91 | 93.51 | 90.17 | 88.60 | 96.68 | 95.07 | 96.90 |
| std (%) | 1.28 | 2.16 | 1.13 | 1.45 | 2.54 | 1.45 | 1.28 | 2.23 | 0.62 |
| Kappa | 0.7913 | 0.8290 | 0.8616 | 0.9028 | 0.7778 | 0.8206 | 0.9397 | 0.9140 | 0.9601 |
| std | 0.0355 | 0.0499 | 0.0345 | 0.0368 | 0.0351 | 0.0289 | 0.0432 | 0.0428 | 0.0138 |
| IP | UP | |||||||
|---|---|---|---|---|---|---|---|---|
| Classifiers | SpMK | ANSSK | ASMSSK | MASEMAP-MKL | SpMK | ANSSK | ASMSSK | MASEMAP-MKL |
| search similar regions | 6.21 | 9.22 | 0.38 | 0.41 | 58.23 | 84.85 | 4.51 | 5.05 |
| kernel computation | 17.59 | 12.50 | 4.61 | 4.68 | 495.17 | 232.33 | 59.06 | 65.55 |
| total | 23.80 | 21.74 | 4.99 | 5.09 | 553.40 | 318.28 | 63.57 | 70.60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; He, C.; Xiang, Y.; Sun, L. Multiscale Adjacent Superpixel-Based Extended Multi-Attribute Profiles Embedded Multiple Kernel Learning Method for Hyperspectral Classification. Remote Sens. 2021, 13, 50. https://doi.org/10.3390/rs13010050
Pan L, He C, Xiang Y, Sun L. Multiscale Adjacent Superpixel-Based Extended Multi-Attribute Profiles Embedded Multiple Kernel Learning Method for Hyperspectral Classification. Remote Sensing. 2021; 13(1):50. https://doi.org/10.3390/rs13010050
Chicago/Turabian StylePan, Lei, Chengxun He, Yang Xiang, and Le Sun. 2021. "Multiscale Adjacent Superpixel-Based Extended Multi-Attribute Profiles Embedded Multiple Kernel Learning Method for Hyperspectral Classification" Remote Sensing 13, no. 1: 50. https://doi.org/10.3390/rs13010050
APA StylePan, L., He, C., Xiang, Y., & Sun, L. (2021). Multiscale Adjacent Superpixel-Based Extended Multi-Attribute Profiles Embedded Multiple Kernel Learning Method for Hyperspectral Classification. Remote Sensing, 13(1), 50. https://doi.org/10.3390/rs13010050