Deep Learning for Land Cover Change Detection
Abstract
:1. Introduction
- Novel Dataset: The majority of studies in remote sensing focuses on only a few available land cover datasets [9]. We present the first land cover change detection study based on a land cover dataset from the federal state of Saxony, Germany [10]. The dataset is characterized by a fine spatial resolution of 3 m to 15 m, a relatively recent creation date, and a representative status in its study region. Therefore, this dataset is highly valuable.
- Innovative Deep Learning Models: While there are successful artificial neural network approaches commonly applied in ML research, these approaches are often not popular in the field of remote sensing [11,12]. We modify and apply fully convolutional neural network (FCN) and long short-term memory (LSTM) network architectures for the particular case of land cover change detection from multitemporal satellite image data. The architectures are successfully applied in other fields of research, and we adapt the findings from these fields for our purpose.
- Innovative Pre-Processing: In remote sensing, there is a need for task-specific pre-processing approaches [5,13,14,15]. We present pre-processing methods to reduce the effect of imbalanced class distributions and varying water levels in inland waters to apply convolutional layers. Further, we discuss the quality and applicability of the applied pre-processing methods for the presented and future studies.
- Comprehensive Change Detection Discussion: No standard evaluation of ML approaches with sequential satellite image input data and a monotemporal GT exists. We present a comprehensive discussion of various statistical methods to evaluate the classification quality and the detected land cover changes.
2. Related Work
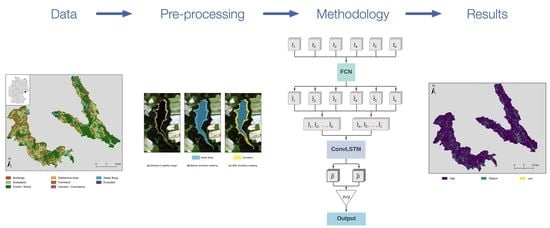
3. Materials and Methods
3.1. Dataset
3.1.1. Land Cover Ground Truth
3.1.2. Sentinel-2 Input Data
3.1.3. Pre-Processing
3.2. Deep Learning Methodology
3.2.1. FCN Networks
- Convolution block: Each of the five convolution blocks consists of several convolution layers; the first two blocks have two, and the last three blocks have four convolution layers. Each convolution layer has a kernel size and uses zero-padding to retain the input’s height and width. The number of filters is consistent in each block. From the first to the fifth block, the filter numbers are .
- MaxPooling: In general, a pooling layer has the purpose of reducing the size of its input. The so-called MaxPooling layer divides each image channel into -chunks and retains the maximum value of each chunk. Therefore, it reduces the height and width of the image by a factor of two.
- Concatenation: In this layer, the upsampled output of the previous decoder stage with the dimensions is concatenated with the output of the convolution block in the encoder stage that has the same height h and width w, but layers. The concatenated output has the dimensions .
- Upsampling layer: The upsampling layer doubles the height and width of an image by effectively replacing each pixel with a -block of pixels with the same value.
- Normalization block: The normalization block consists of two sub-blocks with a convolution layer followed by a batch-normalization layer and a Rectified Linear Unit (ReLu, ) activation layer each. While preserving the input image dimensions, the input activations are re-scaled to have a mean of zero and a standard deviation of one by the batch-normalization layer.
3.2.2. LSTM Networks
3.2.3. Model Training
3.3. Evaluation Methodology
3.3.1. Evaluation Metrics for the 2016 Classification
3.3.2. Evaluation Metrics for the 2018 Classification
- Unison vote: A pixel is classified in unison.
- Absolute majority: The same class is assigned to a pixel in four or five classification maps.
- No majority: There is no class that is assigned to a pixel in four or more classification maps.
4. Results
4.1. Classification Results with 2016 Satellite Data
4.2. Classification Results with 2018 Satellite Data
5. Discussion
5.1. Classification Quality
5.2. Accuracy Evaluation
5.3. Change Detection
5.4. Evaluation of the Pre-Processing
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Percentage of Pixels Classified with | |||
|---|---|---|---|
| Class | High Confidence | Medium Confidence | Low Confidence |
| Buildings | 50.6 | 32.7 | 16.6 |
| Grassland | 72.3 | 20.3 | 7.5 |
| Forest/Wood | 95.4 | 3.4 | 1.2 |
| Settlement Area | 56.9 | 33.7 | 9.4 |
| Farmland | 89.6 | 9.9 | 0.5 |
| Industry/Commerce | 67.2 | 29.2 | 3.6 |
| Water Body | 94.7 | 5.1 | 0.2 |
References
- Green, K.; Kempka, D.; Lackey, L. Using remote sensing to detect and monitor land-cover and land-use change. Photogramm. Eng. Remote Sens. 1994, 60, 331–337. [Google Scholar]
- Loveland, T.; Sohl, T.; Stehman, S.; Gallant, A.; Sayler, K.; Napton, D. A Strategy for Estimating the Rates of Recent United States Land-Cover Changes. Photogramm. Eng. Remote Sens. 2002, 68, 1091–1099. [Google Scholar]
- Yuan, F.; Sawaya, K.E.; Loeffelholz, B.C.; Bauer, M.E. Land cover classification and change analysis of the Twin Cities (Minnesota) Metropolitan Area by multitemporal Landsat remote sensing. Remote Sens. Environ. 2005, 98, 317–328. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Riese, F.M.; Keller, S. Supervised, Semi-Supervised, and Unsupervised Learning for Hyperspectral Regression. In Hyperspectral Image Analysis: Advances in Machine Learning and Signal Processing; Prasad, S., Chanussot, J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Chapter 7; pp. 187–232. [Google Scholar] [CrossRef]
- Riese, F.M. Development and Applications of Machine Learning Methods for Hyperspectral Data. Ph.D. Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2020. [Google Scholar] [CrossRef]
- Foody, G.M.; Pal, M.; Rocchini, D.; Garzon-Lopez, C.X.; Bastin, L. The sensitivity of mapping methods to reference data quality: Training supervised image classifications with imperfect reference data. ISPRS Int. J. Geo-Inf. 2016, 5, 199. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.L.; Aide, T.M.; Riner, G. Land change for all municipalities in Latin America and the Caribbean assessed from 250-m MODIS imagery (2001–2010). Remote Sens. Environ. 2012, 126, 84–103. [Google Scholar] [CrossRef]
- Riese, F.M.; Keller, S.; Hinz, S. Supervised and Semi-Supervised Self-Organizing Maps for Regression and Classification Focusing on Hyperspectral Data. Remote Sens. 2020, 12, 7. [Google Scholar] [CrossRef] [Green Version]
- Staatsbetrieb Geobasisinformation und Vermessung Sachsen (GeoSN). Digitales Basis-Landschaftsmodell. 2014. Available online: http://www.landesvermessung.sachsen.de/fachliche-details-basis-dlm-4100.html (accessed on 28 June 2017).
- Rußwurm, M.; Körner, M. Multi-temporal land cover classification with long short-term memory neural networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 551. [Google Scholar] [CrossRef] [Green Version]
- Rußwurm, M.; Körner, M. Multi-temporal land cover classification with sequential recurrent encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef] [Green Version]
- Camps-Valls, G.; Tuia, D.; Gómez-Chova, L.; Jiménez, S.; Malo, J. Remote sensing image processing. Synth. Lect. Image, Video, Multimed. Process. 2011, 5, 1–192. [Google Scholar] [CrossRef]
- Vidal, M.; Amigo, J.M. Pre-processing of hyperspectral images. Essential steps before image analysis. Chemom. Intell. Lab. Syst. 2012, 117, 138–148. [Google Scholar] [CrossRef]
- Riese, F.M.; Keller, S. Soil Texture Classification with 1D Convolutional Neural Networks based on Hyperspectral Data. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2019, IV-2/W5, 615–621. [Google Scholar] [CrossRef] [Green Version]
- Sefrin, O.; Riese, F.M.; Keller, S. Code for Deep Learning for Land Cover Change Detection; Zenodo: Geneve, Switzerland, 2020. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Keller, S.; Braun, A.C.; Hinz, S.; Weinmann, M. Investigation of the impact of dimensionality reduction and feature selection on the classification of hyperspectral EnMAP data. In Proceedings of the 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. Eurosat: A novel dataset and deep learning benchmark for land use and land cover classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef] [Green Version]
- Leitloff, J.; Riese, F.M. Examples for CNN Training and Classification on Sentinel-2 Data; Zenodo: Geneve, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a transferable change rule from a recurrent neural network for land cover change detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef] [Green Version]
- Interdonato, R.; Ienco, D.; Gaetano, R.; Ose, K. DuPLO: A DUal view Point deep Learning architecture for time series classificatiOn. ISPRS J. Photogramm. Remote Sens. 2019, 149, 91–104. [Google Scholar] [CrossRef] [Green Version]
- Mazzia, V.; Khaliq, A.; Chiaberge, M. Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN). Appl. Sci. 2020, 10, 238. [Google Scholar] [CrossRef] [Green Version]
- Qiu, C.; Mou, L.; Schmitt, M.; Zhu, X.X. Local climate zone-based urban land cover classification from multi-seasonal Sentinel-2 images with a recurrent residual network. ISPRS J. Photogramm. Remote Sens. 2019, 154, 151–162. [Google Scholar] [CrossRef]
- Qiu, C.; Mou, L.; Schmitt, M.; Zhu, X.X. Fusing Multiseasonal Sentinel-2 Imagery for Urban Land Cover Classification With Multibranch Residual Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1787–1791. [Google Scholar] [CrossRef]
- van Duynhoven, A.; Dragićević, S. Analyzing the Effects of Temporal Resolution and Classification Confidence for Modeling Land Cover Change with Long Short-Term Memory Networks. Remote Sens. 2019, 11, 2784. [Google Scholar] [CrossRef] [Green Version]
- Ren, T.; Liu, Z.; Zhang, L.; Liu, D.; Xi, X.; Kang, Y.; Zhao, Y.; Zhang, C.; Li, S.; Zhang, X. Early Identification of Seed Maize and Common Maize Production Fields Using Sentinel-2 Images. Remote Sens. 2020, 12, 2140. [Google Scholar] [CrossRef]
- de Macedo, M.M.G.; Mattos, A.B.; Oliveira, D.A.B. Generalization of Convolutional LSTM Models for Crop Area Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1134–1142. [Google Scholar] [CrossRef]
- Hua, Y.; Mou, L.; Zhu, X.X. Recurrently exploring class-wise attention in a hybrid convolutional and bidirectional LSTM network for multi-label aerial image classification. ISPRS J. Photogramm. Remote Sens. 2019, 149, 188–199. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep Gaussian Process for Crop Yield Prediction Based on Remote Sensing Data. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4559–4566. [Google Scholar]
- Song, A.; Choi, J.; Han, Y.; Kim, Y. Change detection in hyperspectral images using recurrent 3D fully convolutional networks. Remote Sens. 2018, 10, 1827. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal convolutional neural network for the classification of satellite image time series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A deep convolutional coupling network for change detection based on heterogeneous optical and radar images. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 545–559. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar] [CrossRef] [Green Version]
- Rußwurm, M.; Körner, M. Self-attention for raw optical Satellite Time Series Classification. ISPRS J. Photogramm. Remote Sens. 2020, 169, 421–435. [Google Scholar] [CrossRef]
- Yang, X.; Lo, C. Using a time series of satellite imagery to detect land use and land cover changes in the Atlanta, Georgia metropolitan area. Int. J. Remote Sens. 2002, 23, 1775–1798. [Google Scholar] [CrossRef]
- Yang, L.; Xian, G.; Klaver, J.M.; Deal, B. Urban land-cover change detection through sub-pixel imperviousness mapping using remotely sensed data. Photogramm. Eng. Remote Sens. 2003, 69, 1003–1010. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Joshi, A.V. Machine Learning and Artificial Intelligence; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Sefrin, O. Building Footprint Extraction from Satellite Images with Fully Convolutional Networks. Master’s Thesis, Karlsruhe Institute of Technology (KIT), Karlsruhe, Germany, 2020. [Google Scholar]
- Yakubovskiy, P. Segmentation Models. Available online: https://github.com/qubvel/segmentation_models (accessed on 11 November 2019).
- Liu, S.; Shi, Q.; Zhang, L. Few-Shot Hyperspectral Image Classification With Unknown Classes Using Multitask Deep Learning. IEEE Trans. Geosci. Remote. Sens. 2020. [CrossRef]
- Baghbaderani, R.K.; Qu, Y.; Qi, H.; Stutts, C. Representative-Discriminative Learning for Open-set Land Cover Classification of Satellite Imagery. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 1–17. [Google Scholar] [CrossRef]














| Land Cover Class | Spatial Coverage in | Number of Pixels | Percentage of the AOI | Percentage of Intersection with Vector GT |
|---|---|---|---|---|
| Forest/Wood | 86.6 | 866,153 | 36.9 | 96.4 |
| Farmland | 71.6 | 715,608 | 30.5 | 98.4 |
| Grassland | 58.2 | 581,782 | 24.8 | 92.2 |
| Settlement Area | 9.0 | 90,385 | 3.9 | 86.5 |
| Water Body | 4.2 | 41,714 | 1.8 | 98.5 |
| Buildings | 1.3 | 13,247 | 0.6 | 65.7 |
| Industry/Commerce | 1.2 | 11,759 | 0.5 | 83.8 |
| Excluded | 2.3 | 23,752 | 1.0 | 91.0 |
| Model | Trainable Parameters | Diff to VGG-19 in |
|---|---|---|
| VGG-19 (modified) | 20,030,144 | - |
| FCN | 29,064,712 | +45.1 |
| FCN + LSTM | 29,073,992 | +45.2 |
| OA in % | AA in % | Precision in % | in % | ||
|---|---|---|---|---|---|
| Mean Best | 80.5 ± 0.3 81.8 | 69.9 ± 0.6 71.6 | 58.4 ± 0.6 60.1 | 73.5 ± 0.9 74.8 | |
| Mean Best | 82.3 ± 0.8 84.8 | 71.3 ± 3.0 74.7 | 58.6 ± 2.6 62.6 | 75.8 ± 0.8 79.1 | |
| Mean Best | 85.3 ± 0.6 87.0 | 73.0 ± 0.9 73.2 | 62.8 ± 0.6 64.2 | 79.7 ± 0.8 82.0 |
| Voting Basis | Unison | Absolute | Simple or No | Total | |
|---|---|---|---|---|---|
| Consensus of 6 | 6 | 5 or 4 | <4 | ||
| Amount in % | 88.3 | 9.6 | 2.1 | ||
| Agreement with GT in pp | 76.9 | 5.2 | 0.9 | 83.0 | |
| Diff in pp | 11.4 | 4.4 | 1.2 | 17.0 | |
| Amount in % | 85.4 | 11.7 | 2.9 | ||
| Agreement with GT in pp | 75.4 | 6.0 | 1.5 | 82.9 | |
| Diff in pp | 10.0 | 5.7 | 1.4 | 17.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sefrin, O.; Riese, F.M.; Keller, S. Deep Learning for Land Cover Change Detection. Remote Sens. 2021, 13, 78. https://doi.org/10.3390/rs13010078
Sefrin O, Riese FM, Keller S. Deep Learning for Land Cover Change Detection. Remote Sensing. 2021; 13(1):78. https://doi.org/10.3390/rs13010078
Chicago/Turabian StyleSefrin, Oliver, Felix M. Riese, and Sina Keller. 2021. "Deep Learning for Land Cover Change Detection" Remote Sensing 13, no. 1: 78. https://doi.org/10.3390/rs13010078
APA StyleSefrin, O., Riese, F. M., & Keller, S. (2021). Deep Learning for Land Cover Change Detection. Remote Sensing, 13(1), 78. https://doi.org/10.3390/rs13010078