Drone-Based Hyperspectral and Thermal Imagery for Quantifying Upland Rice Productivity and Water Use Efficiency after Biochar Application
Abstract
:1. Introduction
2. Materials and Methods
2.1. Biochar Experiment Plots
2.2. UAV Field Campaign
2.3. Ground Measurements
2.4. Data Processing
2.4.1. Radiometric Correction: Digital Number (DN) to Physical Values
2.4.2. Image Orthorectification and Mosaicking
2.4.3. NDVI and Variations in Gross Primary Productivity (GPP)
2.4.4. Estimation of Shortwave Surface Albedo and Directional Emissivity
2.4.5. Estimation of Land Surface Temperature
2.4.6. Energy Components and Variations in Water Use Efficiency (WUE)
2.4.7. Soil Moisture Content and Soil Matric Potential Estimation
2.4.8. Statistical Analysis
3. Results
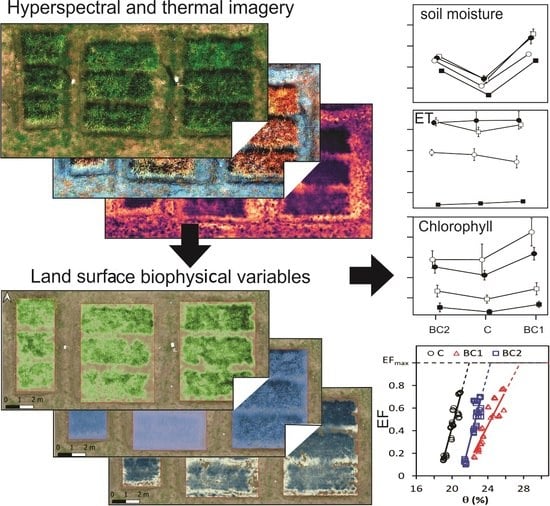
3.1. Hyperspectral and Thermal Imagery
3.2. Variations in Soil Variables after Biochar Application
3.3. Variations in Rice Leaf and Canopy Variables after Biochar Application
3.4. Variations in Evapotranspiration and Land Surface Energy Components
3.5. Comparison of Key Rice Biophysical Variables with Soil Matric Potential.
3.6. Comparison of Evaporative Fraction (EF) with Soil Moisture Content and Matric Potential
4. Discussion
4.1. Biochar Effects on Bare Soil Albedo
4.2. Biochar Effects on Soil Water Availability
4.3. Biochar Effects on Rice Growth Indicators
4.4. Biochar Effects on Evaporative Fraction and Plant WUE
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oliveira, R.A.; Nasi, R.; Niemelainen, O.; Nyholm, L.; Alhonoja, K.; Kaivosoja, J.; Jauhiainen, L.; Viljanen, N.; Nezami, S.; Markelin, L.; et al. Machine learning estimators for the quantity and quality of grass swards used for silage production using drone-based imaging spectrometry and photogrammetry. Remote Sens. Environ. 2020, 246, 111830. [Google Scholar] [CrossRef]
- Dehkordi, R.H.; Denis, A.; Fouche, J.; Burgeon, V.; Cornelis, J.T.; Tychon, B.; Gomez, E.P.; Meersmans, J. Remotely-sensed assessment of the impact of century-old biochar on chicory crop growth using high-resolution UAV-based imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102147. [Google Scholar] [CrossRef]
- Radoglou-Grammatikis, P.; Sarigiannidis, P.; Lagkas, T.; Moscholios, I. A compilation of UAV applications for precision agriculture. Comput. Netw. 2020, 172, 107148. [Google Scholar] [CrossRef]
- Kandylakis, Z.; Falagas, A.; Karakizi, C.; Karantzalos, K. Water Stress Estimation in Vineyards from Aerial SWIR and Multispectral UAV Data. Remote Sens. 2020, 12, 2499. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Y.; Chen, J.; Zhang, Z.; Fu, Q.; Bian, J.; Cui, T.; Ma, Y. Retrieval of cotton plant water content by UAV-based vegetation supply water index (VSWI). Int. J. Remote Sens. 2020, 41, 4389–4407. [Google Scholar] [CrossRef]
- Pipatsitee, P.; Eiumnoh, A.; Praseartkul, P.; Taota, K.; Kongpugdee, S.; Sakulleerungroj, K.; Cha-um, S. Application of infrared thermography to assess cassava physiology under water deficit condition. Plant Prod. Sci. 2018, 21, 398–406. [Google Scholar] [CrossRef]
- Martynenko, A.; Shotton, K.; Astatkie, T.; Petrash, G.; Fowler, C.; Neily, W.; Critchley, A.T. Thermal imaging of soybean response to drought stress: The effect of Ascophyllum nodosum seaweed extract. SpringerPlus 2016, 5, 1393. [Google Scholar] [CrossRef] [Green Version]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Fereres, E.; Villalobos, F. Mapping canopy conductance and CWSI in olive orchards using high resolution thermal remote sensing imagery. Remote Sens. Environ. 2009, 113, 2380–2388. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Morales, A.; Berjón, A.; Agüera, J. Hyperspectral indices and model simulation for chlorophyll estimation in open-canopy tree crops. Remote Sens. Environ. 2004, 90, 463–476. [Google Scholar] [CrossRef]
- Deng, L.; Yan, Y.; Gong, H.; Duan, F.; Zhong, R. The effect of spatial resolution on radiometric and geometric performances of a UAV-mounted hyperspectral 2D imager. ISPRS J. Photogramm. Remote Sens. 2018, 144, 298–314. [Google Scholar] [CrossRef]
- Hagen, N.; Kudenov, M. Review of snapshot spectral imaging technologies. Opt. Eng. 2013, 52, 090901. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Sobejano-Paz, V.; Mikkelsen, T.N.; Baum, A.; Mo, X.; Liu, S.; Köppl, C.J.; Johnson, M.S.; Gulyas, L.; García, M. Hyperspectral and Thermal Sensing of Stomatal Conductance, Transpiration, and Photosynthesis for Soybean and Maize under Drought. Remote Sens. 2020, 12, 3182. [Google Scholar] [CrossRef]
- Yi, Q.; Huang, J.; Wang, F.; Wang, X. Evaluating the performance of PC-ANN for the estimation of rice nitrogen concentration from canopy hyperspectral reflectance. Int. J. Remote Sens. 2010, 31, 931–940. [Google Scholar] [CrossRef]
- Vitrack-Tamam, S.; Holtzman, L.; Dagan, R.; Levi, S.; Tadmor, Y.; Azizi, T.; Rabinovitz, O.; Naor, A.; Liran, O. Random Forest Algorithm Improves Detection of Physiological Activity Embedded within Reflectance Spectra Using Stomatal Conductance as a Test Case. Remote Sens. 2020, 12, 2213. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Mann, C.C. The Real Dirt on Rainforest Fertility. Science 2002, 297, 920–923. [Google Scholar] [CrossRef]
- Lehmann, J. Bio-energy in the black. Front. Ecol. Environ. 2007, 5, 381–387. [Google Scholar] [CrossRef] [Green Version]
- DeLuca, T.H.; MacKenzie, M.D.; Gundale, M.J. Biochar effects on soil nutrient transformations. In Biochar for Environmental Management: Science and Technology; Lehmann, J., Joseph, S., Eds.; Earthscan: London, UK, 2009; pp. 251–270. [Google Scholar]
- Fischer, B.M.C.; Manzoni, S.; Morillas, L.; Garcia, M.; Johnson, M.S.; Lyon, S.W. Improving agricultural water use efficiency with biochar—A synthesis of biochar effects on water storage and fluxes across scales. Sci. Total Environ. 2019, 657, 853–862. [Google Scholar] [CrossRef]
- Lehmann, J. A handful of carbon. Nature 2007, 447, 143–144. [Google Scholar] [CrossRef]
- Lehmann, J.; Rillig, M.C.; Thies, J.; Masiello, C.A.; Hockaday, W.C.; Crowley, D. Biochar effects on soil biota—A review. Soil Biol. Biochem. 2011, 43, 1812–1836. [Google Scholar] [CrossRef]
- Biederman, L.A.; Harpole, W.S. Biochar and its effects on plant productivity and nutrient cycling: A meta-analysis. GCB Bioenergy 2013, 5, 202–214. [Google Scholar] [CrossRef]
- Jeffery, S.; Abalos, D.; Prodana, M.; Bastos, A.C.; van Groenigen, J.W.; Hungate, B.A.; Verheijen, F. Biochar boosts tropical but not temperate crop yields. Environ. Res. Lett. 2017, 12, 053001. [Google Scholar] [CrossRef]
- Durán-Quesada, A.M.; Sorí, R.; Ordoñez, P.; Gimeno, L. Climate Perspectives in the Intra–Americas Seas. Atmosphere 2020, 11, 959. [Google Scholar] [CrossRef]
- Maldonado, T.; Rutgersson, A.; Alfaro, E.; Amador, J.; Claremar, B. Interannual variability of the midsummer drought in Central America and the connection with sea surface temperatures. Adv. Geosci. 2016, 42, 35–50. [Google Scholar] [CrossRef] [Green Version]
- Imbach, P.; Beardsley, M.; Bouroncle, C.; Medellin, C.; Läderach, P.; Hidalgo, H.; Alfaro, E.; Van Etten, J.; Allan, R.; Hemming, D.; et al. Climate change, ecosystems and smallholder agriculture in Central America: An introduction to the special issue. Clim. Chang. 2017, 141, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Fischer, B.M.C.; Morillas, L.; Rojas Conejo, J.; Sánchez-Murillo, R.; Suárez Serrano, A.; Frentress, J.; Cheng, C.H.; Garcia, M.; Manzoni, S.; Johnson, M.S.; et al. Investigating the impacts of biochar on water fluxes in tropical agriculture using stable isotopes. Hydrol. Earth Syst. Sci. Discuss. 2020, 2020, 1–47. [Google Scholar] [CrossRef]
- Agisoft. Agisoft Metashape User Manual: Professional Edition, Version 1.7; Agisoft LLC: St. Petersburg, Russia, 2021; p. 186. [Google Scholar]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Roy, D.; Li, Z.; Zhang, H. Adjustment of Sentinel-2 Multi-Spectral Instrument (MSI) Red-Edge Band Reflectance to Nadir BRDF Adjusted Reflectance (NBAR) and Quantification of Red-Edge Band BRDF Effects. Remote Sens. 2017, 9, 1325. [Google Scholar]
- Köppl, C.J.; Malureanu, R.; Dam-Hansen, C.; Wang, S.; Jin, H.; Barchiesi, S.; Sandí, J.M.S.; Muñoz-Carpena, R.; Johnson, M.; Durán-Quesada, A.M.; et al. Hyperspectral Reflectance Measurements from UAS under Intermittent Clouds: Correcting Irradiance Measurements for Sensor Tilt. Manuscript, in reviewing.
- Köppl, C.J. Thermal Imaging from Unmanned Airborne Vehicles; Technical University of Denmark (DTU): Kgs. Lyngby, Denmark, 2016. [Google Scholar]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Zhou, G. Deriving a light use efficiency estimation algorithm using in situ hyperspectral and eddy covariance measurements for a maize canopy in Northeast China. Ecol. Evol. 2017, 7, 4735–4744. [Google Scholar] [CrossRef]
- Jin, H.; Eklundh, L. In Situ Calibration of Light Sensors for Long-Term Monitoring of Vegetation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3405–3416. [Google Scholar] [CrossRef]
- François, C.; Ottlé, C.; Olioso, A.; Prévot, L.; Bruguier, N.; Ducros, Y. Conversion of 400–1100 nm vegetation albedo measurements into total shortwave broadband albedo using a canopy radiative transfer model. Agronomie 2002, 22, 611–618. [Google Scholar] [CrossRef]
- François, C. The potential of directional radiometric temperatures for monitoring soil and leaf temperature and soil moisture status. Remote Sens. Environ. 2002, 80, 122–133. [Google Scholar] [CrossRef]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. R. Meteorol. Soc. 1996, 122, 1127–1151. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Ibrom, A.; Jakobsen, J.; Josef Köppl, C.; Mallick, K.; Looms, M.C.; Bauer-Gottwein, P. Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion. Remote Sens. 2018, 10, 1978. [Google Scholar] [CrossRef] [Green Version]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating evapotranspiration rates and surface conditions using Landsat TM to estimate atmospheric resistance and surface resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Garcia, M.; Fernández, N.; Villagarcía, L.; Domingo, F.; Puigdefábregas, J.; Sandholt, I. Accuracy of the Temperature–Vegetation Dryness Index using MODIS under water-limited vs. energy-limited evapotranspiration conditions. Remote Sens. Environ. 2014, 149, 100–117. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Guillén-Climent, M.L.; Zarco-Tejada, P.J.; Villalobos, F.J. Estimating Radiation Interception in Heterogeneous Orchards Using High Spatial Resolution Airborne Imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 579–583. [Google Scholar] [CrossRef] [Green Version]
- Austin, R.B.; Blackwell, R.D. Edge and neighbour effects in cereal yield trials. J. Agric. Sci. 1980, 94, 731–734. [Google Scholar] [CrossRef]
- Milliken, G.A.; Johnson, D.E. Analysis of Messy Data. Volume 1: Designed Experiments, 2nd ed.; Chapman & Hall/CRC: New York, NY, USA, 2009. [Google Scholar]
- Tukey, J.W. Exploratory Data Analysis; Addison Wesley Publishing Company: Boston, MA, USA, 1977. [Google Scholar]
- Verheijen, F.G.A.; Jeffery, S.; van der Velde, M.; Penížek, V.; Beland, M.; Bastos, A.C.; Keizer, J.J. Reductions in soil surface albedo as a function of biochar application rate: Implications for global radiative forcing. Environ. Res. Lett. 2013, 8, 044008. [Google Scholar] [CrossRef] [Green Version]
- Bozzi, E.; Genesio, L.; Toscano, P.; Pieri, M.; Miglietta, F. Mimicking biochar-albedo feedback in complex Mediterranean agricultural landscapes. Environ. Res. Lett. 2015, 10, 084014. [Google Scholar] [CrossRef] [Green Version]
- Haider, G.; Steffens, D.; Moser, G.; Müller, C.; Kammann, C.I. Biochar reduced nitrate leaching and improved soil moisture content without yield improvements in a four-year field study. Agric. Ecosyst. Environ. 2017, 237, 80–94. [Google Scholar] [CrossRef]
- Agegnehu, G.; Bass, A.M.; Nelson, P.N.; Bird, M.I. Benefits of biochar, compost and biochar–compost for soil quality, maize yield and greenhouse gas emissions in a tropical agricultural soil. Sci. Total Environ. 2016, 543, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Pallardy, S.G. Absorption of Water and Ascent of Sap. In Physiology of Woody Plants, 3rd ed.; Pallardy, S.G., Ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2008; pp. 287–323. [Google Scholar]
- Manzoni, S.; Vico, G.; Porporato, A.; Katul, G. Biological constraints on water transport in the soil–plant–atmosphere system. Adv. Water Resour. 2013, 51, 292–304. [Google Scholar] [CrossRef]
- Lhomme, J.P.; Elguero, E. Examination of evaporative fraction diurnal behaviour using a soil-vegetation model coupled with a mixed-layer model. Hydrol. Earth Syst. Sci. 1999, 3, 259–270. [Google Scholar] [CrossRef]
- Damm, A.; Paul-Limoges, E.; Haghighi, E.; Simmer, C.; Morsdorf, F.; Schneider, F.D.; van der Tol, C.; Migliavacca, M.; Rascher, U. Remote sensing of plant-water relations: An overview and future perspectives. J. Plant Physiol. 2018, 227, 3–19. [Google Scholar] [CrossRef] [PubMed]









| Variables | Bamboo Biochar BC1 (%) | Sugarcane Biochar BC2 (%) | |
|---|---|---|---|
| Soil variables | Soil moisture content from UAV | 17.7 ± 0.1 | 10.8 ± 0.1 |
| Soil matric potential from UAV 1 | 44.8 ± 0.7 | −66.9 ± 0.7 | |
| Soil albedo | 0.5 ± 0.1 | 1.4 ± 0.1 | |
| Soil surface temperature | −0.7 ± 0.2 | −1.4 ± 0.2 | |
| Leaf and canopy variables | Gross primary productivity | 41.9 ± 3.4 | 17.5 ± 3.4 |
| Normalized difference vegetation index | 10.0 ± 1.4 | 7.4 ± 1.4 | |
| Canopy chlorophyll content | 32.0 ± 3.0 | 10.1 ± 3.0 | |
| Water use efficiency | 40.8 ± 3.5 | 13.4 ± 3.5 | |
| Leaf area index | 6.0 ± 1.3 | −4.9 ± 1.3 | |
| Land surface energy components | Net radiation | −0.2 ± 0.3 | 2.3 ± 0.3 |
| Latent heat flux (evapotranspiration) | 1.1 ± 1.0 | 4.0 ± 1.0 | |
| Evaporative fraction | 3.7 ± 1.0 | − 0.2 ± 1.0 | |
| Ground heat flux | −1.8 ± 0.6 | 3.5 ± 0.6 | |
| Sensible heat flux | −0.4 ± 0.7 | −0.4 ± 0.7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.; Köppl, C.J.; Fischer, B.M.C.; Rojas-Conejo, J.; Johnson, M.S.; Morillas, L.; Lyon, S.W.; Durán-Quesada, A.M.; Suárez-Serrano, A.; Manzoni, S.; et al. Drone-Based Hyperspectral and Thermal Imagery for Quantifying Upland Rice Productivity and Water Use Efficiency after Biochar Application. Remote Sens. 2021, 13, 1866. https://doi.org/10.3390/rs13101866
Jin H, Köppl CJ, Fischer BMC, Rojas-Conejo J, Johnson MS, Morillas L, Lyon SW, Durán-Quesada AM, Suárez-Serrano A, Manzoni S, et al. Drone-Based Hyperspectral and Thermal Imagery for Quantifying Upland Rice Productivity and Water Use Efficiency after Biochar Application. Remote Sensing. 2021; 13(10):1866. https://doi.org/10.3390/rs13101866
Chicago/Turabian StyleJin, Hongxiao, Christian Josef Köppl, Benjamin M. C. Fischer, Johanna Rojas-Conejo, Mark S. Johnson, Laura Morillas, Steve W. Lyon, Ana M. Durán-Quesada, Andrea Suárez-Serrano, Stefano Manzoni, and et al. 2021. "Drone-Based Hyperspectral and Thermal Imagery for Quantifying Upland Rice Productivity and Water Use Efficiency after Biochar Application" Remote Sensing 13, no. 10: 1866. https://doi.org/10.3390/rs13101866
APA StyleJin, H., Köppl, C. J., Fischer, B. M. C., Rojas-Conejo, J., Johnson, M. S., Morillas, L., Lyon, S. W., Durán-Quesada, A. M., Suárez-Serrano, A., Manzoni, S., & Garcia, M. (2021). Drone-Based Hyperspectral and Thermal Imagery for Quantifying Upland Rice Productivity and Water Use Efficiency after Biochar Application. Remote Sensing, 13(10), 1866. https://doi.org/10.3390/rs13101866