Algorithm for Real-Time Cycle Slip Detection and Repair for Low Elevation GPS Undifferenced Data in Different Environments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Wide-Lane Phase Minus Narrow-Lane Pseudorange (WL-NL) Combination with Pseudorange Multipath
2.2. Inaccurate Detection of Cycle Slip by Conventional MW Combination
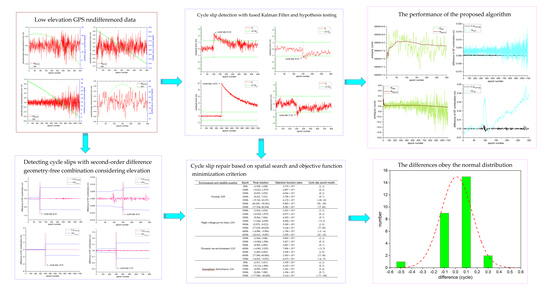
2.3. Cycle Slip Detection with Fused Kalman Filter and Hypothesis Testing
2.4. Detecting Cycle Slips with Second-Order Difference Geometry-Free Combination Considering Elevation
2.5. Cycle Slip Repair Based on Spatial Search and Objective Function Minimization Criterion
- Round the float value calculated by Equation (25) as the initial value of the cycle slip.
- The effects of low elevation and ionospheric disturbance period are fully considered, the initial value of cycle slip is taken as the center, ±5 cycles is the search range, and one cycle is the search step, in order to form a cycle slip candidate combination.
- Use the cycle slip candidate combination constructed in Step 2 to repair the carrier phase observation in real time, then re-check it through the cycle slip detection methods proposed in this study, and store the cycle slip combination that the two cycle slip detection methods meet the condition of no cycle slip simultaneously.
- Use the cycle slip combination that meets the detection condition to repair the carrier phase observation, and substitute the repaired carrier phase into the objective function, so that the set of cycle slip combinations that makes the objective function in Equation (26) meet the minimization criterion is the correct cycle slip solution.
3. Results
3.1. Measured GPS Data in Four Different Environments
3.1.1. Normal Environment
3.1.2. High-Voltage Transmission Lines Environment
3.1.3. Dynamic Environment in the Sea Area
3.1.4. Ionospheric Disturbance Environment
3.2. Validation of Cycle Slip Detection and Repair Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bisnath, S.; Kim, D.; Langley, R. A new approach to an old problem: Carrier phase cycle slips. GPS World 2001, 13, 42–49. [Google Scholar]
- Lee, H.K.; Wang, J.L.; Rizos, C. Effective cycle slip detection and identification for high precision GPS/INS integrated systems. J. Navig. 2003, 56, 475–486. [Google Scholar] [CrossRef] [Green Version]
- Karaim, M.; Karamat, T.; Noureldin, A.; Ei-Shafie, A. GPS cycle slip detection and correction at measurement level. Br. J. Appl. Sci. Technol. 2014, 4, 4239–4251. [Google Scholar]
- Wang, Z.; Wang, X.; Ji, S.; Chen, W. Optimal cycle slip detection and correction with reliability. Surv. Rev. 2016, 48, 233–239. [Google Scholar] [CrossRef]
- Liu, Z.Z. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J. Geod. 2011, 85, 171–183. [Google Scholar]
- Wei, H.; Li, J.C.; Zhang, S.J.; Xu, X.Y. Cycle slip detection and repair for dual-frequency LEO satellite GPS carrier phase observations with orbit dynamic model information. Remote Sens. 2019, 11, 1273. [Google Scholar] [CrossRef] [Green Version]
- Zhen, D. MATLAB software for GPS cycle-slip processing. GPS Solut. 2012, 16, 267–272. [Google Scholar]
- Liu, Z.Z. A new approach for cycle slip detection and fix using single GPS receiver’s single satellite dual frequency data containing arbitrarily large pseudorange errors. J. Glob. Pos. Syst. 2018, 16, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Lichtenegger, H.; Hofmann-Wellenhof, B. GPS-data preprocessing for cycle-slip detection. In Global Positioning System: An Overview; Springer: Berlin/Heidelberg, Germany, 1990; pp. 57–68. [Google Scholar]
- Ju, B.; Gu, D.F.; Chang, X.; Herring, T.; Duan, X.J.; Wang, Z.M. Enhanced cycle slip detection method for dual-frequency BeiDou GEO carrier phase observations. GPS Solut. 2017, 21, 1227–1238. [Google Scholar] [CrossRef]
- Li, B.F.; Liu, T.X.; Nie, L.W.; Qin, Y.N. Single-frequency GNSS cycle slip estimation with positional polynomial constraint. J. Geod. 2019, 93, 1781–1803. [Google Scholar] [CrossRef]
- Blewitt, G. An Automatic Editing Algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Lacy, M.; Reguzzoni, M.; Sanso, F.; Venuti, G. The Bayesian detection of discontinuities in a polynomial regression and its application to the cycle-slip problem. J. Geod. 2008, 82, 527–542. [Google Scholar] [CrossRef]
- Melbourne, W.G. The case for ranging in GPS based geodetic systems. In Proceedings of the 1st International Symposium on Precise Positioning with the Global Positioning System, Rockville, ML, USA, 15–19 April 1985; pp. 373–386. [Google Scholar]
- Hatch, R. The synergism of GPS code and carrier measurements. In Proceedings of the Third International Symposium on Satellite Doppler Positioning at Physical Sciences Laboratory of New Mexico State University, Las Cruces, NM, USA, 8–12 February 1982; pp. 1213–1231. [Google Scholar]
- Gao, Y.; Li, Z.F. Cycle slip detection and ambiguity resolution algorithms for dual-frequency GPS data processing. Mar. Geod. 1999, 22, 169–181. [Google Scholar]
- Ji, S.Y.; Chen, W.; Weng, D.J.; Wang, Z.J.; Ding, X.L. A study on cycle slip detection and correction in case of ionospheric scintillation. Adv. Space Res. 2013, 51, 742–753. [Google Scholar] [CrossRef]
- Cai, C.S.; Liu, Z.Z.; Xia, P.F.; Dai, W.J. Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity. GPS Solut. 2013, 17, 247–260. [Google Scholar] [CrossRef]
- Chen, D.Z.; Ye, S.R.; Zhou, W.; Liu, Y.Y.; Jiang, P.; Tang, W.M.; Yuan, B.; Zhao, L.W. A double-differenced cycle slip detection and repair method for GNSS CORS network. GPS Solut. 2016, 20, 439–450. [Google Scholar] [CrossRef]
- Ji, S.Y.; Wang, Z.J.; Chen, W.; Weng, D.j.; Xu, Y.; Fan, S.J.; Huang, B.H.; Sun, G.Y.; Wang, H.Q.; He, W.Y. Geometry-free and non-geometry-free testing quantities for cycle slip detection and correction in case of strong atmospheric variations with static observations. Surv. Rev. 2014, 335, 104–111. [Google Scholar] [CrossRef]
- Tang, L.; Zheng, K.; Li, X.X. Analysis of geometry-free residuals in case of traveling ionosphere disturbances and their impact cycle slip detection. GPS Solut. 2017, 21, 1221–1226. [Google Scholar] [CrossRef]
- Luo, X.M.; Liu, Z.Z.; Lou, Y.D.; Gu, S.F.; Chen, B.Y. A study of multi-GNSS ionospheric scintillation and cycle-slip over Hong Kong region for moderate solar flux conditions. Adv. Space Res. 2017, 60, 1039–1053. [Google Scholar] [CrossRef]
- Miao, Y.; Sun, Z.W.; Wu, S.N. Error analysis and cycle-slip detection research on satellite-borne GPS observation. J. Aerosp. Eng. 2011, 24, 95–101. [Google Scholar] [CrossRef]
- Li, P.; Jiang, X.Y.; Zhang, X.H.; Ge, M.R.; Schuh, H. Kalman-filter-based undifferenced cycle slip estimation in real-time precise point positioning. GPS Solut. 2019, 23, 99. [Google Scholar] [CrossRef]
- Ye, S.R.; Liu, Y.Y.; Song, W.W.; Lou, Y.D.; Yi, W.T.; Zhang, R.; Jiang, P.; Xiang, Y. A cycle slip fixing method with GPS + GLONASS observations in real-time kinematic PPP. GPS Solut. 2016, 20, 101–110. [Google Scholar] [CrossRef]
- Bisnath, S.B. Efficient automated cycle-slip correction of dual-frequency kinematic GPS data. In Proceedings of the Institute of Navigation GPS 2000, Salt Lake City, UT, USA, 19–22 September 2000; pp. 145–154. [Google Scholar]
- Yang, Y.; Hatch, R.R.; Sharpe, R.T. GPS multipath mitigation in measurement domain and its applications for high accuracy navigation. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Long Beach, CA, USA, 21–24 September 2004. [Google Scholar]
- Farrell, J.; Givargis, T. Differential GPS reference station algorithm—Design and analysis. IEEE Trans. Contr. Syst. Technol. 2000, 8, 519–531. [Google Scholar] [CrossRef]
- Bastos, L.; Landau, H. Fixing cycle slips in dual-frequency kinematic GPS-applications using Kalman filtering. Manuscr. Geod. 1988, 13, 249–256. [Google Scholar]
- Lin, S.G.; Yu, F.C. Cycle slips detection algorithm for low cost single frequency GPS RTK positioning. Surv. Rev. 2013, 330, 206–214. [Google Scholar] [CrossRef]
- Mertikas, S.P.; Rizos, C. On-line detection of abrupt changes in the carrier-phase measurements of GPS. J. Geod. 1997, 71, 469–482. [Google Scholar] [CrossRef]
- Yu, X.; Gao, J. Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations. ISPRS Int. J. GeoInf. 2017, 6, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Ansari, K. Real-Time Positioning Based on Kalman Filter and Implication of Singular Spectrum Analysis. IEEE Geosci. Remote Sens. Lett. 2021, 18, 58–61. [Google Scholar] [CrossRef]
- Fujita, S.; Saito, S.; Yoshihara, T. Cycle slip detection and correction methods with time-differenced model for single frequency GNSS applications. Trans. Inst. Syst. Control. Inf. Eng. 2013, 26, 8–15. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. Quality control in integrated navigation systems. IEEE Aerosp. Electron. Syst. Mag. 2002, 5, 35–41. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, Y.H.; Zhou, L.T.; Huang, D.F.; Hassan, A. Fast cycle slip determination for high-rate multi-GNSS RTK using modified geometry-free phase combination. GPS Solut. 2020, 24, 42. [Google Scholar] [CrossRef]
- Qian, C.; Liu, H.; Zhang, M.; Shu, B.; Xu, L.W.; Zhang, R.F. A geometry-based cycle slip detection and repair method with time-differenced carrier phase (TDCP) for a single frequency Global Position System (GPS) + BeiDou navigation satellite system (BDS) receiver. Sensors 2016, 16, 2064. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, W.H.; Wang, J.L. A real-time cycle slip repair method using the multi-epoch geometry-based model. GPS Solut. 2021, 25, 60–71. [Google Scholar] [CrossRef]






















| Environment and Satellite Number | Sampling Rate | Epoch | Cycle Slip Pairs |
|---|---|---|---|
| Normal, G09 | 15 s | 50th | (1, 1) |
| 100th | (0, 2) | ||
| 150th | (0, 1) | ||
| 200th | (9, 7) | ||
| 250th | (−10, 10) | ||
| 300th | (50, −50) | ||
| 350th | (77, 60) | ||
| High-voltage power lines, G03 | 1 s | 100th | (1, 1) |
| 150th | (0, 2) | ||
| 200th | (9, 7) | ||
| 250th | (−5, 5) | ||
| 300th | (1, 0) | ||
| 350th | (77, 60) | ||
| 400th | (−5, −4) | ||
| 450th | (10, −10) | ||
| Dynamic sea environment, G10 | 5 s | 100th | (1, 1) |
| 200th | (0, 2) | ||
| 300th | (9, 7) | ||
| 400th | (−5, 5) | ||
| 500th | (1, 0) | ||
| 600th | (77, 60) | ||
| 700th | (−4, −5) | ||
| Ionospheric disturbance, G26 | 30 s | 50th | (1, 1) |
| 100th | (0, 2) | ||
| 150th | (5, 4) | ||
| 200th | (9, 7) | ||
| 250th | (−77, −60) |
| Environment and Satellite Number | Epoch | Float Solution | Objective Function Value | Cycle Slip Search Results |
|---|---|---|---|---|
| Normal, G09 | 50th | (1.038, 1.038) | 3.719 × 10−3 | (1, 1) |
| 100th | (−0.021, 1.979) | 6.897 × 10−2 | (0, 2) | |
| 150th | (0.035, 1.035) | 4.656 × 10−2 | (0, 1) | |
| 200th | (9.022, 7.022) | 5.780 × 10−3 | (9, 7) | |
| 250th | (−9.743, 10.257) | 6.176 × 10−2 | (−10, 10) | |
| 300th | (49.439, −50.561) | 9.803 × 10−2 | (50, −50) | |
| 350th | (77.334, 60.334) | 9.281 × 10−2 | (77, 60) | |
| High-voltage power lines, G03 | 100th | (1.024, 1.024) | 1.022 × 10−4 | (1, 1) |
| 150th | (−0.020, 1.979) | 6.975 × 10−2 | (0, 2) | |
| 200th | (9.066, 7.066) | 6.292 × 10−2 | (9, 7) | |
| 250th | (−5.042, 4.958) | 4.904 × 10−1 | (−5, 5) | |
| 300th | (0.978, −0.022) | 3.560 × 10−2 | (1, 0) | |
| 350th | (77.020, 60.020) | 3.144 × 10−2 | (77, 60) | |
| 400th | (−4.996, −3.996) | 1.784 × 10−2 | (−5, −4) | |
| 450th | (10.013, −9.987) | 2.059 × 10−2 | (10, −10) | |
| Dynamic sea environment, G10 | 100th | (1.046, 1.046) | 9.862 × 10−4 | (1, 1) |
| 200th | (−0.004, 1.996) | 5.427 × 10−3 | (0, 2) | |
| 300th | (8.992, 6.992) | 3.087 × 10−2 | (9, 7) | |
| 400th | (−4.965, 5.035) | 7.906 × 10−3 | (−5, 5) | |
| 500th | (1.063, 0.063) | 3.188 × 10−3 | (1, 0) | |
| 600th | (77.084, 60.084) | 2.363 × 10−2 | (77, 60) | |
| 700th | (−4.051, −5.051) | 6.672 × 10−2 | (−4, −5) | |
| Ionospheric disturbance, G26 | 50th | (1.017, 1.017) | 1.358 × 10−4 | (1, 1) |
| 100th | (−0.114, 1.886) | 6.133 × 10−2 | (0, 2) | |
| 150th | (4.995, 3.995) | 2.241 × 10−1 | (5, 4) | |
| 200th | (9.080, 7.080) | 1.196 × 10−1 | (9, 7) | |
| 250th | (−77.006, −60.006) | 2.114 × 10−1 | (−77, −60) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N.; Zhang, Q.; Zhang, S.; Wu, X. Algorithm for Real-Time Cycle Slip Detection and Repair for Low Elevation GPS Undifferenced Data in Different Environments. Remote Sens. 2021, 13, 2078. https://doi.org/10.3390/rs13112078
Liu N, Zhang Q, Zhang S, Wu X. Algorithm for Real-Time Cycle Slip Detection and Repair for Low Elevation GPS Undifferenced Data in Different Environments. Remote Sensing. 2021; 13(11):2078. https://doi.org/10.3390/rs13112078
Chicago/Turabian StyleLiu, Ning, Qin Zhang, Shuangcheng Zhang, and Xiaoli Wu. 2021. "Algorithm for Real-Time Cycle Slip Detection and Repair for Low Elevation GPS Undifferenced Data in Different Environments" Remote Sensing 13, no. 11: 2078. https://doi.org/10.3390/rs13112078
APA StyleLiu, N., Zhang, Q., Zhang, S., & Wu, X. (2021). Algorithm for Real-Time Cycle Slip Detection and Repair for Low Elevation GPS Undifferenced Data in Different Environments. Remote Sensing, 13(11), 2078. https://doi.org/10.3390/rs13112078