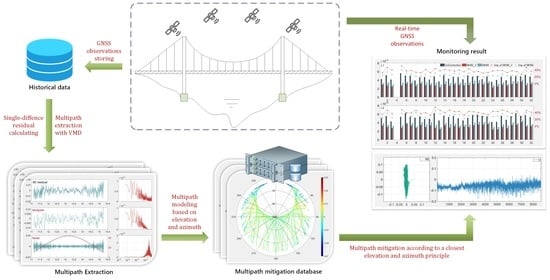
An Improved Multipath Mitigation Method and Its Application in Real-Time Bridge Deformation Monitoring

Abstract

A multipath is a major error source in bridge deformation monitoring and the key to achieving millimeter-level monitoring. Although the traditional MHM (multipath hemispherical map) algorithm can be applied to multipath mitigation in real-time scenarios, accuracy needs to be further improved due to the influence of observation noise and the multipath differences between different satellites. Aiming at the insufficiency of MHM in dealing with the adverse impact of observation noise, we proposed the MHM_V model, based on Variational Mode Decomposition (VMD) and the MHM algorithm. Utilizing the VMD algorithm to extract the multipath from single-difference (SD) residuals, and according to the principle of the closest elevation and azimuth, the original observation of carrier phase in the few days following the implementation are corrected to mitigate the influence of the multipath. The MHM_V model proposed in this paper is verified and compared with the traditional MHM algorithm by using the observed data of the Forth Road Bridge with a seven day and 10 s sampling rate. The results show that the correlation coefficient of the multipath on two adjacent days was increased by about 10% after residual denoising with the VMD algorithm; the standard deviations of residual error in the L1/L2 frequencies were improved by 37.8% and 40.7%, respectively, which were better than the scores of 26.1% and 31.0% for the MHM algorithm. Taking a ratio equal to three as the threshold value, the fixed success rates of ambiguity were 88.0% without multipath mitigation and 99.4% after mitigating the multipath with MHM_V. The MHM_V algorithm can effectively improve the success rate, reliability, and convergence rate of ambiguity resolution in a bridge multipath environment and perform better than the MHM algorithm.

1. Introduction

The global navigation and positioning system (GNSS) is widely used in many high-precision positioning fields, including traditional surveying and mapping, deformation monitoring, etc. The double difference model can eliminate satellite clock error, receiver clock error, and carrier hardware delay, and greatly weakens the ionospheric delay, tropospheric delay, orbit error, and other distance-related errors [1,2,3]. Therefore, a positioning accuracy at the millimeter level can be achieved for a short baseline. However, a multipath is difficult to parameterize and cannot be eliminated or mitigated by the differential method; thus, it has become a major error source in GNSS high-precision applications.

For bridge deformation monitoring, the location of the monitoring station is selected mainly according to the needs of deformation monitoring, which means the influence of a multipath cannot be avoided by selecting an installation place, and it can only be mitigated by hardware-based or software-based methods. Hardware-based methods mitigate multipath signals mainly by adding choke or improving antenna gain, but only part of the multipath delay can be eliminated, which may increase the noise level in measurements and reduce the SNR (Signal Noise Ratio). There are three kinds of methods based on software: (1) multipath mitigation models or stochastic models based on SNR; (2) multipath filtering on the coordinate domain; and (3) multipath mitigation based on its spatial and temporal repeatability.

Methods based on SNR include using SNR to weaken the mirror multipath in GPS multicarrier phase measurement [4], quantifying a multipath by the amplitude and frequency of SNR data [5], and detecting and eliminating most of the multipath based on pre-calibrated SNR values [6]. Multipath filtering methods based on the coordinate domain refer mainly to the use of noise reduction methods to separate multipath signals and noises in the coordinate time series, such as wavelet analysis [7], Kalman filtering [8], and the Vondrak filter with cross validation [9,10]. Although this kind of method can separate multipaths simply and effectively, it is only suitable for a static observation environment, because the above filtering method cannot distinguish a multipath from actual station displacement.

Multipath mitigation methods based on spatial–temporal repeatability include sidereal filtering (SF) and look-up tables (also known as MHM). The SF algorithm was first proposed in 1992 [11] and is based on the repeated constellations of GPS satellites every sidereal day. It is satellite-dependent and is realized by the observation of sidereal lag time (in the time domain). The orbit repetition period based on the GPS constellation is fixed and is generally considered to be about 23 h, 56 min, and 4 s [12,13]. The accuracy of SF in the coordinate domain is improved by calculating the actual average orbital repetition period of satellites [14,15]. Although SF has been widely used, due to the different orbital periods of different constellations and the effects of orbital maneuvers, the accuracy of multipath mitigation is reduced in the process of practical application [16].

The MHM algorithm is based mainly on the fact that the multipath is related to the elevation and azimuth of the satellites only, and it uses the repeatability of the satellite orbit in the hemispherical area. The model is established based on the correction value in each grid according to the multi-day post-processing multipath and is used to revise the carrier observation to mitigate the multipath [17,18]. The purpose of calculating the average value of the multipath in each grid is to ensure that the observation noises are weakened. Currently, conventional MHM algorithms mostly use a constant elevation and azimuth resolution to construct multipath spatial maps, such as 5° × 2° [19], 1° × 1° [15,20], and 0.5° × 0.5° [21]. There are also some ways of using a variable spatial resolution, such as comprehensively considering the geometric and statistical characteristics of signal propagation to establish grids of a similar size and shape to ensure that a grid with high elevation also has enough data [22]. Furthermore, the grid is divided into three parts according to the height angle; when a grid with a size of 0.2°/0.2°/1° is adopted, the positioning accuracy is improved by about 12% compared with the traditional MHM algorithm [23]. However, through the data analysis, it can be seen that the multipath of the same satellite still has an obvious change trend, even in a grid of 1° × 1°. Therefore, it is not sufficiently rigorous to calculate the mean value of a multipath in a grid to weaken the influence of noise.

Therefore, in this study, we use the filtering algorithm to denoise SD residuals in order to improve the accuracy of the multipath mitigation model [24,25,26,27]. There are some denoising methods that are commonly used, including wavelet transform (WT) [7,28,29], empirical mode decomposition (EMD) [30,31], adaptive filtering (AF) [32], etc. However, the accuracy of WT is greatly affected by the selection of the wavelet basis function and the determination of the threshold value. EMD is easily affected by signal interruption, which leads to the modal aliasing problem and the existence of an endpoint effect [33]. The convergence effect and computational efficiency of AF cannot be well guaranteed. However, the variational mode decomposition (VMD) algorithm can adaptively extract signal components from any non-linear and non-stationary signals due to its non-recursive frequency-domain solution method. Therefore, the decomposition accuracy is high, and the modal aliasing problem and endpoint effect can be avoided [34]. Moreover, each signal component after decomposition has its physical significance. At present, the VMD algorithm is used mainly in mechanical fault diagnosis [35,36,37]; there are also a few applied research works with GNSS, such as reducing the impact of ionospheric scintillation on GNSS positioning [38] and extracting low-frequency trend terms from GNSS time series [39]. The VMD algorithm has excellent performance in terms of signal denoising and low-frequency trend extraction.

Based on the above analysis, this study uses the single difference model to calculate the SD residuals of each satellite and then utilizes the VMD algorithm to extract the multipath. Based on the historical multipath data, the multipath mitigation model is established, and the real-time GNSS carrier phase is corrected with the multipath mitigation model according to the principle of the closest elevation and azimuth. Section 2 introduces the characteristics of the multipath and SD residual extraction method based on the SD model and describes the denoising and multipath extraction principle of the VMD algorithm and the algorithm flow of multipath mitigation, which is called MHM_V, based on the MHM algorithm. Section 3 shows the effect of the MHM_V algorithm on multipath mitigation in the actual environment of a bridge and compares it with the general MHM algorithm. Finally, the Section 4 and Section 5 give a summary and perspectives on this paper.

2. Materials and Methods

2.1. The Characteristics and Extraction of a Multipath

2.1.1. The Characteristics of a Multipath

The received GNSS phase signal is the superposition of electromagnetic waves from a direct path and multiple indirect paths from the reflection and diffraction effects of surrounding objects. These effects are called multipath effects. The size and frequency of a multipath can be expressed as follows [40]:

$$\begin{array}{c}\Delta {\phi }_j=\arctan [\cos \theta /({\alpha }^{-1}+\sin \theta )]\\ f_{{\phi }_j}=\frac{2h}{{\lambda }_j}\stackrel{·}{\theta }\cos \theta \end{array}$$

(1)

where $\Delta {\phi }_j$ and $f_{{\phi }_j}$ represent the carrier-phase error and the frequency of a multipath caused by indirect signals at frequency $j$, respectively, ${\lambda }_j$ represents the wavelength of a carrier observation at frequency $j$, $h$ represents the vertical distance from the receiver antenna phase center to the reflection plane, $\alpha$ is the refraction coefficient of the reflection plane, $\theta$ is the elevation of the satellite, and $\stackrel{·}{\theta }$ is the elevation change rate of the satellite. It can be seen from the above formula that the multipath is related to the relative position of the satellite and the reflector only. Due to the repeatability of the satellite orbit, it is obvious that the multipath has repeatability in both time and space. In addition, the multipath delay increases with the decrease of satellite elevation, which means that low-elevation satellites are more vulnerable to the multipath effect. In addition, the frequency of the multipath is higher for low-elevation satellites.

2.1.2. The Extraction of SD Residuals Based on the SD Model

The satellite s is observed by two stations, k and l, together. By calculating the difference of the observations at the j frequency of the satellite, the observation equation of the difference between stations can be obtained.

$$\begin{array}{c}\Delta P_{j,kl}^s=\Delta {\rho }_{kl}^s+c\cdot \Delta d{t}_{kl}^s+{\mu }_j\cdot \Delta I_{kl}^s+\Delta T_{kl}^s+\Delta d_{j,kl}+\Delta M_{j,kl,p}^s+\Delta e_{j,kl}^s\\ \Delta {\varphi }_{j,kl}^s=\Delta {\rho }_{kl}^s+c\cdot \Delta d{t}_{kl}^s-{\mu }_j\cdot \Delta I_{kl}^s+\Delta T_{kl}^s+{\lambda }_j(\Delta N_{j,kl}^s+\Delta {\delta }_{j,kl}^s)+\Delta M_{j,kl,\varphi }^s+\Delta e_{j,kl}^s\end{array}$$

(2)

where $\Delta$ represents the single difference operator, $P$ and $\varphi$ represent the pseudorange and carrier-phase observations, respectively, $\rho$ represents the station–satellite distance, $c$ represents the speed of light, $dt$ represents the clock error, $\mu$ represents the ionospheric delay coefficient, $I$ represents ionospheric delay, $T$ represents tropospheric delay, $\lambda$ represents the wavelength, $N$ represents the carrier-phase ambiguity, $\delta$ represents the carrier-phase hardware delay deviation, $d$ represents the pseudorange hardware delay, $e$ represents observation noise, and $M_P$ and $M_{\varphi }$ represent the multipath delay of the pseudorange and carrier-phase, respectively. The satellite clock error, pseudorange, and carrier-phase hardware delay deviation can be eliminated by the inter-station difference, and spatial correlation errors such as satellite orbit error, ionospheric delay, and tropospheric delay can be weakened at the same time.

Due to the existence of the carrier-phase hardware delay deviation $\Delta \delta$, the single difference ambiguity absorbs its influence and loses its integer characteristic. Therefore, the reference satellite can be added, and the clock error parameters can be re-parameterized to ensure the integer solvability of the ambiguity. The equivalent clock error after re-parameterization is as follows:

$$\begin{array}{c}c\cdot \Delta d{t}_{j,kl,P}=c\cdot \Delta d{t}_{kl}+\Delta d_{j,kl}\\ c\cdot \Delta d{t}_{j,kl,\varphi }=c\cdot \Delta d{t}_{kl}+{\lambda }_j(\Delta N_{j,kl}^r+\Delta {\delta }_{j,kl})\end{array}$$

(3)

where $d{t}_{j,kl,P}$ and $d{t}_{j,kl,\varphi }$ denote the pseudorange and carrier-phase clock error after re-parameterization, respectively, and the superscript $r$ represents the reference satellite. At the same time, for the bridge deformation monitoring scene, the distance between the reference station and the monitoring point is relatively close (usually less than 3 km), and the single residual error of the ionosphere and troposphere is negligible, so Equation (1) can be rewritten as follows:

$$\begin{array}{c}\Delta P_{j,kl}^s=\Delta {\rho }_{kl}^s+c\cdot \Delta d{t}_{j,kl,P}^s+\Delta M_{j,kl,p}^s+\Delta e_{j,kl}^s\\ \Delta {\varphi }_{j,kl}^s=\Delta {\rho }_{kl}^s+c\cdot \Delta d{t}_{j,kl,\varphi }^s+{\lambda }_j\Delta \nabla N_{j,kl}^{sr}+\Delta M_{j,kl,\varphi }^s+\Delta e_{j,kl}^s\end{array}$$

(4)

For the short baseline, the DD ambiguity can be fixed by the DD model combined with filtering; only the equivalent clock error and coordinate deviation can be estimated, and the carrier and pseudorange single error residual of each satellite can be obtained at the same time. Generally speaking, these residuals reflect the relationship between the multipath error of satellite observations and the satellite altitude angle and azimuth angle. However, it can be seen from Equation (3) that the residual calculated by the SD model not only includes the multipath of each satellite but also includes the observation noise. Therefore, the spatial map established by using the residual of each satellite directly cannot represent the true value of the multipath.

2.2. The Improved MHM Algorithm (MHM_V)

Because the value of the carrier-phase multipath is basically about 2 cm, and the carrier noise can reach 5 mm or even higher, it is necessary to denoise the extracted satellite residuals to ensure the accuracy of the multipath spatial map. The traditional MHM algorithm takes the mean value of the multipath delay of the same satellite in the same grid to achieve the denoising effect. However, it can be seen from Figure 1 that, even in the grid of 1° × 1° (ELE_AZI: 12_26°), the multipath also has an obvious changing trend, so the way in which the traditional MHM algorithm deals with noise is unreasonable. At the same time, it can be seen that the multipath is independent of the satellite, which means that the multipaths of different satellites in the same grid are quite different. Therefore, in this study, the VMD algorithm is used to denoise the SD residuals to obtain a multipath with higher accuracy, and the multipath correction model is established based on this. Then the principle of the nearest azimuth of elevation is used to correct the carrier observations in order to mitigate the multipath. The above-improved MHM algorithm is called MHM_V in this paper.

2.2.1. The Introduction of VMD

The VMD algorithm decomposes a non-stationary sequence into multiple relatively stationary sub-sequences with different frequency scales by constructing and solving a variational problem. It is assumed that the input signal $f$ is decomposed into $K$ modal functions $u_k(t)$. In order to minimize the sum of the bandwidth estimates of each mode, the signal $f$ is equal to the sum of all modes, and the constrained variational problem is described as follows:

$$\begin{array}{c}\underset{\left\{{{\displaystyle u}}_k\right\},\left\{{{\displaystyle v}}_k\right\}}{\min }\left\{{\displaystyle \sum _{k=1}^K{‖{\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)*{{\displaystyle u}}_k(t)\right]e^{-j{\omega }_{k}t}‖}_2^2}\right\}\\ s.t. {\displaystyle \sum _{k=1}^K{u}_k(t)=x(t)}\end{array}$$

(5)

where $\left\{u_k\right\}=\left\{u_1,\cdots u_k\right\},\left\{{\omega }_k\right\}=\left\{{\omega }_1,\cdots {\omega }_k\right\}$ are the set of all mode functions and their center frequencies, respectively; ${\partial }_t$ is the partial derivative of time $t$ for the function; $\delta \left(t\right)$ is the pulse function; $j$ is an imaginary unit; $*$ represents convolution.

The modal components and center frequencies are optimized by using the Alternating Direction Multiplier (ADMM) iterative algorithm and Parseval/Plancherel Fourier equidistant transformation. Then, searching for the saddle points of the augmented Lagrange function, after alternate optimization iterations, the expressions of $u_k$, $\lambda$, and ${\omega }_k$ can be obtained as follows:

$${\widehat{u}}_k^{n+1}\left(\omega \right)=\frac{\widehat{f}\left(\omega \right)-{\displaystyle {\sum }_{i\ne k}{\widehat{u}}_i\left(\omega \right)+\frac{{\widehat{\lambda }}^n\left(\omega \right)}{2}}}{1+2\alpha {\left(\omega -{\omega }_k^n\right)}^2}$$

(6)

$${\widehat{\lambda }}^{n+1}\left(\omega \right)={\widehat{\lambda }}^n\left(\omega \right)+\tau \left(\widehat{f}\left(\omega \right)-{\displaystyle \sum _{k=1}^K{\widehat{u}}_k^{n+1}(\omega )}\right)$$

(7)

$${\omega }_k^{n+1}=\frac{{\displaystyle {\int }_o^{\infty }\omega {\left|{\widehat{u}}_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }}{{\displaystyle {\int }_o^{\infty }{\left|{\widehat{u}}_k^{n+1}\left(\omega \right)\right|}^{2}d\omega }}$$

(8)

where ${\widehat{u}}_k^{n+1}\left(\omega \right)$ is the winning filter of the current surplus $\widehat{f}\left(\omega \right)-{\displaystyle {\sum }_{i\ne k}{\widehat{u}}_i\left(\omega \right)}$, and ${\omega }_k^{n+1}$ is the center of gravity of the modal power spectrum. By an inverse Fourier transform of ${\widehat{u}}_k^{}\left(\omega \right)$, the real part of the result is the time domain modal component $u_k^{}\left(\omega \right)$. The detailed derivation process can be found in [20]. The VMD algorithm used to decompose the SD residual time series is shown in Algorithm 1.

Algorithm 1: VMD algorithm used to decompose the SD residual time series

1: Initialize $\left\{{\widehat{u}}_k^1\right\},\left\{{\widehat{\omega }}_k^1\right\},{\widehat{\lambda }}^1,n\leftarrow 0$, where n is the iteration number.

2: repeat the entire cycle, $n\leftarrow n+1$.

3:  For $k=1:K$ do

4:   Update ${\widehat{u}}_k^1$ for all $w\ge 0$, using Equation (6);

5:   Update ${\omega }_k$, using Equation (8);

6:  end for

7:  Do dual ascent for all $w\ge 0$, using Equation (7);

8: until Iterative constraints satisfied: ${{\displaystyle {\sum }_k{‖{\widehat{u}}_k^{n+1}-{\widehat{u}}_k^n‖}_2^2/‖{\widehat{u}}_k^n‖}}_2^2<\epsilon$

2.2.2. The Algorithm Flow of MHM_V

The traditional MHM algorithm uses historical data to establish the multipath grid and then corrects the current observations according to the spatial repeatability of the multipath. During the data processing, the mean value of the multipath delay in the same grid is taken as the final multipath correction value to weaken the influence of the observation noise. The general grid size is 1° × 1° (elevation × altitude). Some scholars have tried other different grid sizes, such as 2° × 2° or 5° × 5°, while other scholars set the grid size according to the height angle. Although the above method can weaken the influence of observation noise to a certain extent, it does not take into account the change of the multipath delay in the same grid and the problem of having less multipath correction information in a grid with low sampling rate data. Therefore, in this study, we attempt to solve the problem by using the advantages of the VMD algorithm for non-stationary time series denoising, directly removing the observation noise from the multipath correction data and retaining the multipath change trend in one grid. In addition, the new algorithm no longer relies on the establishment of the multipath grid but matches the multipath correction value according to the principle of the nearest elevation and azimuth, which solves the problem of insufficient multipath correction information with low sampling rate observation data.

In conclusion, the MHM_V algorithm proposed in this paper is based on VMD denoising and the nearest elevation and azimuth (closest EZ) strategy, which includes the following steps. The algorithm flow of the MHM_V model is shown in Figure 2:

• The dynamic model is used to calculate the current daily observation data, and the integer solution of ambiguity and three-dimensional coordinates are obtained based on the double-difference model.
• The integer ambiguity and three-dimensional coordinates in step 1 are substituted into the single-difference model, and the single-difference residuals of all satellites are obtained.
• The multipath is extracted from the SD residual by the VMD algorithm, and the multipath mitigation model is established and stored in the database.
• In the case that the multipath mitigation model has been established, using the principle of the nearest elevation and azimuth, the multipath correction value is searched from the database, corrected to the double difference observation, and then steps 1–3 are repeated.

3. Results

To verify the performance of the suggested MHM_V method, a case study was carried out on the Forth Road Bridge, which was opened in 1964 and spans the Firth of Forth, connecting Edinburgh to Fife. It has an overall length of 2.5 km and a main span length of 1006 m between the two main towers. Two monitoring stations (SHM2 and SHM3) are located at the midspan on the east and west sides of the bridge, respectively. As shown in Figure 3, the reference station (SHM1) is set on the south side of the bridge and is approximately 1500 m from the monitoring stations on the midspan.

The real 0.1 Hz GPS data for seven consecutive days (DOY 2019:291–297) contributed to the analysis of the multipath in the bridge deformation monitoring conditions. The monitoring station and the reference station had the same type of receiver and antenna: Leica Geosystem GR 10 GNSS receivers and LEIAR 10 antennas. The broadcast ephemerides were used to assess the satellite ORTs in real time. The effects from troposphere, ionosphere, phase windup, and satellite orbital errors could be considered as negligible due to the short baseline. The dual-frequency SD algorithm was used in the data processing, and the ambiguities of each epoch were resolved by a Kalman filter. Moreover, the ratio and the success rate were used to evaluate the quality of the least-squares ambiguity decorrelation adjustment (LAMBDA) method. With all ambiguities resolved, the fixed ambiguities were substituted into the observation equation; then, the coordinates of the monitoring station could be calculated using the least squares (LS) method, and the residual of carrier observation of each satellite could be obtained at the same time.

3.1. Multipath Extraction

First, the single difference model mentioned in Section 2.2 was used to calculate the SD residuals of the baseline SHM1–SHM2 (1.5 km). We selected satellite G14 and G32 as representatives for analysis, and the results are shown in Figure 4.

Figure 4 shows the SD carrier-phase residuals of G14 and G32 for L1 and L2 frequencies calculated by the SD model. The upper two panels represent the SD residuals of satellite G14, the lower two panels represent the SD residuals of satellite G32, the blue solid line represents the residuals of carrier-phase L1, the red solid line represents carrier-phase L2, and the green solid line represents the satellite elevation. As depicted in Figure 4, the SD residuals were about 2 cm, mainly including the multipath and observation noises. Figure 4 also illustrates that the multipath increased with the decrease of elevation, which is also the reason why it was difficult to fix the ambiguity of low-elevation satellites. Furthermore, it can be seen from Figure 4 that the carrier-phase multipaths of different frequencies or different satellites were not correlated. Therefore, we needed to establish the spatial multipath maps of each frequency and each satellite separately.

Since the calculated carrier-phase SD residuals mainly included the multipath and noise, we used the VMD algorithm to separate the two features to improve the accuracy of the extracted multipath. The left panels of Figure 5 display the decomposed results of G14, and the right panels are the results of G32. The blue solid lines from top to bottom represent the SD residual, extracted multipath, and carrier-phase noise, respectively, and the red solid lines represent the corresponding spectrum maps. As shown in Figure 5, the separated noise had a negative correlation with the satellite elevation, which means that the carrier-phase noise increased obviously with the decrease in satellite elevation, further conforming to the characteristics of carrier-phase noise.

In addition, in order to further analyze the accuracy of the VMD algorithm in multipath extraction, this study calculated the SD carrier-phase residuals (abbreviated SD_res) of L1/L2 for all the satellites on seven consecutive days (DOY 2019: 291–297). At the same time, the multipath extracted by the VMD algorithm was obtained (abbreviated MP_vmd). Then, the correlation coefficients of SD_res and MP_vmd of all satellites on two adjacent days from DOY 291–297 were analyzed. The results are illustrated in Figure 6.

As shown in Figure 6, the red line represents the correlation coefficient of MP_vmd, and the blue line represents the correlation coefficient of SD_res. It was found that the correlation coefficient of MP_vmd was higher than SD_res, which further indicates that the multipath extracted by VMD algorithm eliminated the influence of noise and was able to describe the multipath of all satellites more accurately. Algorithm 1 lists the average value of correlation coefficients of all satellites on two adjacent days from DOY 291–297. As summarized in

Table 1. Mean correlations of carrier phase for all satellites between DOY 291 and 297.

DOY	L1			L2
	SD_res	MP_VMD	Promotion Ratio	SD_res	MP_VMD	Promotion Ratio
291–292	0.763	0.843	11.2%	0.778	0.861	10.8%
292–293	0.757	0.840	11.1%	0.787	0.871	10.6%
293–294	0.734	0.812	10.7%	0.766	0.848	10.7%
294–295	0.677	0.738	9.0%	0.722	0.796	10.2%
295–296	0.719	0.788	9.7%	0.748	0.824	10.2%
296–297	0.780	0.866	11.1%	0.795	0.883	11.0%

, the correlation coefficient of MP_vmd was about 10% higher than SD_res. The correlation coefficient of MP_vmd was about 80%, and even up to 88%.

Similar to the MHM algorithm, a multipath spatial map was established for the MP_vmd and SD_res of DOY 296. It can be seen from Figure 7 that the relatively large multipath delay was mainly distributed below the elevation of 30°, and the satellites with an elevation above 45° were barely affected by the multipath. Due to the north-south trend of the bridge, a multipath is distributed on both sides of the east and the west and presents symmetry.

Figure 8 shows the residuals of satellite G14 before and after the multipath correction during a complete observation period on DOY 297. The left panel represents the residual of the L1 carrier-phase, the right panel represents the residual of the L2 carrier-phase, the red solid line represents the uncorrected residual, the black solid line represents the residual mitigated by MHM_V, and the blue solid line represents the residual mitigated by MHM. The uncorrected residual series display the unsystematic and frequent fluctuations together with high-frequency noises. After multipath mitigation, the residual series tended toward a Gaussian distribution of white noise and removed mostly low-frequency variations.

It can be seen from the frequency distribution histogram in Figure 9 that the residuals after using MHM_V for multipath correction were more concentrated near 0, and almost all residuals were within ±1 cm. Taking the L1 carrier-phase as an example, the proportion of residual error less than 1 cm before multipath mitigation is only 89.6%, and the proportion after multipath mitigation with MHM is increased to 96.3%; finally, the proportion after multipath mitigation with MHM_V is as high as 98.2%.

As shown in Figure 10, the mitigation effect of MHM_V on the multipath was about 10% higher than that of MHM, and the residual improvement ratio of L2 was better than that of carrier L1. For the MHM_V model, the reduction percentage increased from one day to five days, then stabilized at a 40% level (Figure 10). For the MHM model, the reduction percentage increased from one day to six days (about 30%) and finally stabilized, which was consistent with the conclusion of Dong et al. (2016). Therefore, in the next experiment, the multipath correction model was established based on the data of the previous six days (DOY 291–296) and was applied to the resolution of DOY 297.

In contrast to the traditional MHM algorithm, the MHM_V algorithm proposed in this paper did not need to establish a spatial grid, because the algorithm adopts the nearest elevation and azimuth principle for multipath matching and mitigation. This means that it was not necessary to consider the influence of the large multipath variation in the same grid.

Utilizing the MHM algorithm and the improved MHM_V algorithm to correct the multipath, the effect of the two algorithms was evaluated according to the RMS value of each satellite carrier-phase residual. As illustrated in Figure 11, the RMS value of the carrier-phase residual using the MHM_V algorithm was smaller. Furthermore, the RMS of the carrier-phase residual mitigated with the MHM_V algorithm was reduced by 37.8% and 40.7% compared to that without multipath mitigation, while the RMS of the carrier-phase residual mitigated with the MHM algorithm was reduced by 26.1% and 31.0%, which shows that MHM_V algorithm had a better effect on multipath mitigation. At the same time, it can be seen from Figure 12a that the multipath correction of the MHM_V algorithm was more obvious for low-elevation satellites, for which most of the multipath could be eliminated.

Meanwhile, according to the multipath mitigation results, the relationship between GPS L1/L2 carrier-phase noise and satellite elevation was analyzed, and the results are shown in Figure 12b. In Figure 12b, the horizontal axis represents the elevation, and the vertical axis represents the standard deviation of residuals mitigated with MHM_V, which were considered as observation noise. Then, we used the exponential function model to fit the noise. The red solid line in the figure represents the fitting function ($f(x)=0.0015+0.0062*e^{-\frac{x}{0.3456}}$, where $x$ represents the elevation), the fitting residual was 0.2 mm, and the correlation coefficient was 97%, which shows that the noises fully conformed to the commonly used random model of elevation. The stochastic model was also used in the subsequent positioning experiments.

3.2. Analysis of Ambiguity Resolution Results

The data of DOY 297 were selected for the positioning experiment, the data from the six days from DOY 291 to DOY 296 were used to establish the multipath correction model, and the multipath correction was carried out according to the strategy in Section 3.2. The ratio value of ambiguity resolution is shown in Figure 13, where red spots indicate the ratio value after the multipath was mitigated by the MHM_V algorithm, and dark color spots indicate the ratio value without correction for the multipath. The sharp drop in the ratio was due to the launching of a new satellite. The multipath directly affects the value of the floating ambiguity solution bias, which even can lead to the fixing failure or fixing error of ambiguities in severe circumstances. Taking a ratio equal to three as the threshold value, the fixed success rate of ambiguity was 88.0% without multipath mitigation and 99.4% after mitigating the multipath using the MHM_V algorithm proposed in this paper.

Figure 14 illustrates the floating ambiguity bias; it can be seen that after using the MHM_V algorithm to mitigate the multipath, the time required for all floating ambiguity biases less than 0.5 weeks (convergence time) was shorter, and the floating ambiguity bias after convergence was smaller than that without multipath mitigation. According to the results of the ratio value and floating ambiguity bias, the MHM_V algorithm is proven to accelerate the convergence of ambiguity and improve the success rate and reliability of ambiguity fixing.

4. Discussion

Multipath mitigation is the key to achieving millimeter accuracy in bridge deformation monitoring. As these effects are highly related to the relative position of satellites and the observation environment, there are some mitigation methods, such as sidereal filtering (AF) based on the time periodicity of a multipath and multipath hemispherical map (MHM) based on the spatial periodicity, which are suitable for real-time application. According to the analysis of the spatial distribution characteristics of the multipath, the deficiency of the existing MHM algorithm is pointed out, although the influence of observation noise can be weakened by averaging the multipaths in one grid (defined by the elevation and azimuth); however, the variation of multipaths in the same grid cannot be ignored, as shown in Figure 1.

In contrast to the idea that the MHM algorithm takes the average value of multipath delay in the same grid to reduce the influence of observation noise, this paper proposes the use of the VMD algorithm to directly denoise the multipath delay. It can be seen from Figure 5 that the separated noise component completely conforms to the characteristics of white noise, showing that the multipath delay extracted by the VMD algorithm has higher accuracy. At the same time, combined with the analysis results of the multipath correlation coefficients on two adjacent days, it can also be seen that the VMD algorithm achieved a better denoising effect. This shows that the VMD algorithm can better assist in the improvement of the accuracy of the multipath-weakened model.

In addition, this study uses the measured data of the bridge to evaluate the effect of MHM and MHM_V on the weakening of the multipath. From the positioning residuals in Figure 8 and Figure 10, it can be seen that the positioning residuals corrected by MHM_V were smaller, and the low-frequency sequence was significantly corrected. It can also be seen from the final positioning experiment that the MHM_V algorithm significantly improved the fixed ratio value of the ambiguity and the floating-point solution deviation of the ambiguity. The weakening effect of MHM_V on the multipath was verified from many aspects.

5. Conclusions

Aiming at the insufficiency of the traditional MHM algorithm in dealing with the effect of observation noise on multipath mitigation, and taking advantage of the spatial repeatability of a multipath in a fixed environment, this research proposed the MHM_V model based on the VMD algorithm. First, the VMD algorithm is used to mitigate the carrier-phase noise in SD residual, and the multipath is extracted to establish a multipath correction model and store it in the database. Then, according to the principle of the closest elevation and azimuth, the original observations of the carrier-phase in the next few days are corrected to mitigate the influence of the multipath. Finally, the model is applied to bridge deformation monitoring, and the performance in terms of ambiguity resolution is confirmed.

In this study, seven days of observation data of the Forth Road bridge (DOY 2019: 291–297) were used to verify the proposed algorithm. First, the single difference model was used to extract the carrier-phase residuals of each satellite, and then the VMD algorithm was used to separate the multipath and carrier-phase noise of SD residuals. The results showed that the correlation coefficient of multipath delay extracted by the VMD algorithm was more than 80%, and the highest was 88%. Compared with the correlation coefficient of the single-difference residual error, the MP_vmd was closer to the real multipath. Then, we compared the mitigation effect of MHM_V and MHM algorithms. The standard deviations of residual error for the L1/L2 frequencies were improved by 37.8% and 40.7%, respectively, which were better than the scores of 26.1% and 31.0% for MHM. After multipath mitigation utilizing the MHM_V algorithm, the proportion reached 98.2% for the absolute L1 residual less than 1 cm, compared with 96.3% using the MHM algorithm, and 89.6% without multipath mitigation. The carrier-phase residual was greatly improved. Finally, through the ratio and float ambiguity bias of ambiguity resolution, it was seen that the MHM_V algorithm could effectively improve the success rate, reliability, and convergence rate of ambiguity fixing in a bridge multipath environment. Taking a ratio equal to three as the threshold value, the fixed success rate of ambiguity was 88.0% without multipath mitigation and 99.4% after mitigating the multipath using the MHM_V algorithm proposed in this paper, which means that the MHM_V algorithm performs well in multipath mitigation in bridge deformation monitoring.

The experimental data used in this study are GNSS observations with a 10 s sampling rate, which cannot reflect high-frequency multipath delay. Due to the lack of time and space resolution, the accuracy of the multipath correction model is reduced. Therefore, the MHM_V algorithm proposed in this paper can have a better effect when used with high sampling rate data. In addition, because the location of monitoring points on the bridge exhibited significant vibration, the improvement of positioning accuracy due to the multipath mitigation model cannot be evaluated by standard deviation, and it may need to be verified by observation data in a static environment to determine the quantitative index.