Next Article in Journal
Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm
Previous Article in Journal
Detection of Changes in Arable Chernozemic Soil Health Based on Landsat TM Archive Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 12
10.3390/rs13122414
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm

by
Lijun Chao
1,2,3,
Ke Zhang
1,2,4,*,
Jingfeng Wang
5,
Jin Feng
4 and
Mengjie Zhang
6
1
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, China
2
Yangtze Institute for Conservation and Development, Hohai University, Nanjing 210098, China
3
College of Agricultural Science and Engineering, Hohai University, Nanjing 210098, China
4
College of Hydrology and Water Resources and CMA-HHU Joint Laboratory for Hydro-Meteorological Studies, Hohai University, Nanjing 210098, China
5
School of Civil and Environmental Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
6
Department of Earth and Environmental Engineering, Columbia University, New York, NY 10027, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(12), 2414; https://doi.org/10.3390/rs13122414
Submission received: 17 May 2021 / Revised: 15 June 2021 / Accepted: 17 June 2021 / Published: 20 June 2021
(This article belongs to the Section Environmental Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Evapotranspiration (ET) is a vital part of the hydrological cycle and the water–energy balance. To explore the characteristics of five typical remote sensing evapotranspiration datasets and provide guidance for algorithm development, we used reconstructed evapotranspiration (Recon) data based on ground and GRACE satellite observations as a benchmark and evaluated five remote sensing datasets for 592 watersheds across the continental United States. The Global Land Evaporation Amsterdam Model (GLEAM) dataset (with bias and RMSE values of 23.18 mm/year and 106.10 mm/year, respectively), process-based land surface evapotranspiration/heat flux (P-LSH) dataset (bias = 22.94 mm/year and RMSE = 114.44 mm/year) and the Penman–Monteith–Leuning (PML) algorithm generated ET dataset (bias = −17.73 mm/year and RMSE = 108.97 mm/year) showed the better performance on a yearly scale, followed by the model tree ensemble (MTE) dataset (bias = 99.45 mm/year and RMSE = 141.32 mm/year) and the moderate-resolution imaging spectroradiometer (MODIS) dataset (bias = −106.71 mm/year and RMSE = 158.90 mm/year). The P-LSH dataset outperformed the other four ET datasets on a seasonal scale, especially from March to August. Both PML and MTE showed better overall accuracy and could accurately capture the spatial variability of evapotranspiration in arid regions. The P-LSH and GLEAM products were consistent with the Recon data in middle-value section. MODIS and MTE had larger bias and RMSE values on a yearly scale, whereby the MODIS and MTE datasets tended to underestimate and overestimate ET values in all the sections, respectively. In the future, the aim should be to reduce bias in the MODIS and MTE algorithms and further improve seasonality of the ET estimation in the GLEAM algorithm, while the estimation accuracy of the P-LSH and MODIS algorithms should be improved in arid regions. Our analysis suggests that combining artificial intelligence algorithms or data-driven algorithms and physical process algorithms will further improve the accuracy of ET estimation algorithms and the quality of ET datasets, as well as enhancing their capacity to be applied in different climate regions.

Graphical Abstract

1. Introduction

Evapotranspiration (ET) usually consumes 60–70% of land precipitation [1,2] and nearly 50% of solar radiation on a global scale [3,4]. Therefore, ET is the dominant component of the global water and energy cycle [5,6,7]. Accurate estimation of ET is crucial for understanding hydrological and ecological processes [8,9], agricultural drought detection and mitigation, and planning of water resources [10]. ET data are also essential for predicting extreme weather events and exploring the relationships between atmosphere, hydrosphere, and biosphere systems [11].
In situ monitoring of ET has been conducted for centuries using a variety of methods [12], including the Bowen ratio, lysimeters, laser isotopes, and eddy covariance [12]. Although these methods can provide long-term point- or local-scale observations, they cannot provide ET data at regional and global scales [13,14]. ET data derived from satellite remote sensing observations at regional or global scales has become essential in the study of hydrology and ecology because of its advantages in respect of spatial coverage [15,16,17].
The development of remote sensing technology since the 1970s has greatly promoted ET models at the point scale or single vegetation types at the regional scale [18]. There are four main methods for satellite remote sensing of ET: the statistical model, the energy balance model, data assimilation, and the Penman–Monteith model based on surface energy balance [19]. The statistical model played an important role in early studies of the satellite remote sensing of ET; however, the regression relationships between ET and remote sensing parameters are not formulated on the basis of underlying physical mechanisms [20].
The energy balance model is a remote sensing method widely used for ET estimation, which uses latent heat flux to estimate ET as the remaining part of the energy balance equation [21,22]. The underlying surface can be considered as a whole, or it can be divided into single-layer or double-layer models [23]. The single-layer model ignores the internal structure and characteristics of the underlying surface and considers the soil and vegetation as a whole to study the surface water and energy balance and is also known as the big-leaf model [24]. The most representative models are the surface energy balance algorithm for land (SEBAL) [25] and the surface energy balance system (SEBS) [26]. Considering the different surface temperatures of soil and vegetation, the sensible heat fluxes of the two are calculated separately. Shuttleworth and Wallace [23] proposed a two-layer energy model in 1985. The theoretical mechanism of the double-layer model is more applicable than the single-layer model, and it can adapt to the complex underlying surface conditions. However, the estimation of sensible heat flux has one limitation which is the energy cannot be closed, leading to insufficient accuracy in simulation and calculation [27].
Although remote sensing data can provide land surface parameters on a large scale, the underlying surface parameters are not obtained in the presence of clouds [28]. To obtain a continuous spatiotemporal ET dataset, the spatial and temporal resolutions of remote sensing data are usually disaggregated. Building the land data assimilation system with the physical mechanism allows continuously introducing satellite remote sensing data into the land surface model (LSM), thereby providing a new method for ET estimation [29,30].
Among the many methods of estimating ET, the Penman–Monteith formula combines the principle of energy balance and aerodynamics on the basis of ignoring the horizontal transmission of water vapor [31]. It has a strong physical foundation and can better simulate ET, and it is recommended by the Food and Agriculture Organization (FAO) [32]. Penman [33] first proposed the Penman formula in 1948, while in 1965 Monteith [34] introduced canopy resistance to characterize the influence of soil moisture and vegetation growth on latent heat flux, as well as estimate ET of an unsaturated surface. The core of the Penman–Monteith formula is the estimation of surface water vapor diffusion (canopy) resistance [35].
The application of remote sensing technology realizes the estimation of surface resistance on a large scale [36]. Cleugh, et al. [37] believe that the normalized difference vegetation index (NDVI), leaf area index (LAI), and vegetation fraction (FC) represent vegetation characteristics of the underlying surface without water stress. They implemented the calculation of surface resistance based on the remote sensing of three vegetation characteristics. To improve the canopy conductance equation, Mu, et al. [38,39] constructed the Penman–Monteith–Mu model and used MODIS remote sensing and meteorological datasets to estimate global ET by considering temperature and saturated vapor pressure. Using the process-based land surface evapotranspiration/heat flux algorithm (P-LSH), a global long-term (1982–2013) ET dataset was generated [7,40]. Leuning, et al. [41] developed the Penman–Monteith–Leuning (PML) model by introducing a soil evaporation model and improving the Gash modification of the Penman–Monteith model (PM-Gs). Zhang, et al. [42] developed a coupled diagnostic biophysical model named PML-V2 and generated 500 m and 8-day resolution global ET data from July 2002 to August 2017. Miralles, et al. [43] and Martens, et al. [44] compiled a set of algorithms to build the Global Land Evaporation Amsterdam Model (GLEAM) dedicated to the estimation of terrestrial evaporation and root-zone soil moisture from satellite data.
In addition, some intelligent algorithms have been used to estimate global ET [45], including artificial intelligence algorithms and machine learning algorithms [46,47,48,49]. A machine learning algorithm (the model tree ensemble, MTE) was used to estimate the ET dataset on a global scale from 1982 to 2008 by compiling a global monitoring network, along with meteorological and remote sensing observations [48].
Since there are many existing satellite ET retrieval algorithms and associated global ET datasets, it is important to understand the accuracy and limitation of these datasets and provide insights for the ET retrieval algorithm development. Most of the past studies are focused on evaluating the different ET algorithms/datasets by comparing them with ground observations [50] and intercomparison [19,51]. A recent study developed a method [52] to reconstruct high-quality basin-scale actual evapotranspiration values from the ground and Gravity Recovery and Climate Experiment (GRACE) observations based on water balance, providing new benchmark data to evaluate the global ET datasets on basin scale across the continental United States (CONUS). Therefore, the objectives of this study are twofold: (1) to evaluate five widely used global ET products on multiple time scales by comparing them with the reconstructed ET data from 2003 to 2008 for 592 watersheds across the CONUS based on the ground and GRACE observations, and (2) to identify the relative advantages/disadvantages of the five ET algorithms and their future improvement directions. To this end, the following sections are organized as follows: Section 2 explains the data and methodology; Section 3 summarizes results; Section 4 is the discussion, and Section 5 presents the conclusions.

2. Data and Methodology

2.1. Study Area and Data

We chose the CONUS as the case study area, targeting 592 watersheds (Figure 1) distributed in 12 regions, comprising the Arkansas–Red Basin, California–Nevada, Colorado Basin, Lower Mississippi, Middle Atlantic, Missouri Basin, North Central, Northeast, Northwest, Ohio, Southeast, and West Gulf. The spatial resolution of the study area was set to 0.125°.
It has a continental climate in most of the CONUS and a subtropical climate in its south. The climate of the CONUS becomes warmer as one travels further south, and drier the further west until one reaches the West Coast. The topography of the CONUS is high in the west and low in the east. There are many rivers and lakes in the CONUS, and the water systems are complex. In general, they can be divided into three major water systems, including the Atlantic water system, the Pacific water system, and the Great Lakes of North America. The Atlantic water system located in the east of the Rocky Mountains includes the Mississippi River, the Connecticut River, and the Hudson River. The Pacific water system includes the Colorado River, the Columbia River, and the Yukon River. Based on the National Land Cover Database 2011 (NLCD2011), the eastern part of the CONUS is dominated by deciduous forests, while the west is dominated by evergreen forests. Shrubs are distributed in the western and southwestern regions of the CONUS, and woody wetlands are distributed near the Great Lakes and the eastern coastline. Farmland and grassland account for most of the land cover of the Great Plains [53].
Five ET datasets, including the reconstructed ET (Recon) as the benchmark, were used in this study (Table 1). The water balance equation was used to calculate reconstructed ET on the basis of ground and GRACE satellite observations as the residual of the water balance equation 52]. The precipitation data were obtained from the Parameter Elevation Regressions on Independent Slopes Model (PRISM). The monthly mean streamflow data were all from United States Geological Survey (USGS) stream gauging stations. The monthly water storage data were obtained from the GRACE satellite. The Recon data were obtained from April 2002 to September 2013 with a spatial resolution of 0.125° and a monthly temporal resolution.
The global ET data [7,40] were generated using the process-based land surface evapotranspiration/heat fluxes algorithm (P-LSH), including the modified Penman–Monteith model for canopy transpiration and soil evaporation and the Priestley–Taylor model for open-water evaporation, referred to as P-LSH, from January 1982 to December 2013 (Table 1). Using the Jarvis–Stewart-type canopy conductance model, biome-specific canopy conductance was determined from the NDVI. The spatiotemporal resolution of P-LSH was 0.5° and monthly.
Zhang, et al. [54] used the Leuning surface conductance model together with the Penman–Monteith model to estimate transpiration from the plant canopy and obtained a global ET dataset named PML-V1 from 1981 to 2012. A water–carbon coupled canopy conductance model was used to estimate transpiration, and a global ET dataset named PML-V2 was generated from July 2002 to August 2019 with a spatial resolution of 500 m and 8-day temporal resolution [42] (hereafter referred to as PML) (Table 1).
Mu et al. developed an ET algorithm using MODIS and global meteorology data to obtain MODIS global ET datasets [38,39]. The MODIS global ET data with a spatial resolution of 500 m and temporal resolution of 8 days are hereafter referred to as MODIS (Table 1).
The model tree ensemble (MTE) approach featured the model tree induction algorithm (TRIAL) and evolving trees with random growth algorithm (ERROR) [48]. The MTE approach used a global monitoring network of continuous in situ measurements, along with meteorological data and remote sensing observations, to obtain a global ET dataset with a spatial resolution of 0.5° and monthly temporal resolution from 1982 to 2008 [45,55] (hereafter referred to as MTE) (Table 1).
Miralles et al. used the Priestley and Taylor (PT) evaporation model to estimate global scale ET with a spatial resolution of 0.25° and a temporal resolution of daily, monthly, and yearly [43]. This model aims to make the best use of satellite observations to estimate the evaporation flux on land continuously in space. The temporal cover of GLEAM dataset is from 1980 to 2020 (Table 1).
The five ET datasets and Recon have different spatial and temporal resolutions. For the convenience of comparison, the spatial resolution of all comparisons is 0.125°, and the temporal resolution is month, season, and year. On the time scale, the PML and MODIS were accumulated from 8 days to month. All the data with a resolution different from 0.125° were resampled to a 0.125° resolution. For these datasets with a coarser resolution, linear interpolation is applied to produce their corresponding 0.125° data. For these datasets with a finer resolution, area-weighted aggregation is applied. The ET value of each watershed is the mean value of all grid cells falling within the watershed.

2.2. Methodology

Each remote sensing ET dataset for each watershed was equal to the average value of all grid cells falling within the watershed, and all comparisons were on the watershed scale. The comparison of temporal scales included the yearly, seasonal, and monthly scales. To investigate whether the performance of the five remote sensing ET datasets varied in space, we further compared the spatial distribution of multiyear average annual ET, multiyear mean seasonal ET, and correlation coefficients between Recon and the five remote sensing ET datasets on a monthly scale. On the monthly scale, we compared not only the spatial correlation and significance level but also the accuracies of the five ET datasets using the Taylor diagram. The spatial distributions of four seasons and areal average ET values are used to evaluate five ET datasets on a seasonal scale. On the yearly scale, we use scatter density maps and spatial distributions to evaluate the five ET datasets comparing the Recon data. To evaluate the accuracies of the five remote sensing ET datasets (P-LSH, PML, MODIS, MTE, and GLEAM), three statistical metrics were used to compare their quality to the Recon data: bias, root-mean-square error (RMSE), and correlation coefficient (R). Bias and RMSE allowed evaluating the error and accuracy of the five remote sensing ET datasets, while R characterized the degree of fit between the five remote sensing ET datasets and Recon data. When the bias and RMSE are smaller, the result is better. Conversely, a smaller R indicates a bad result.

3. Results

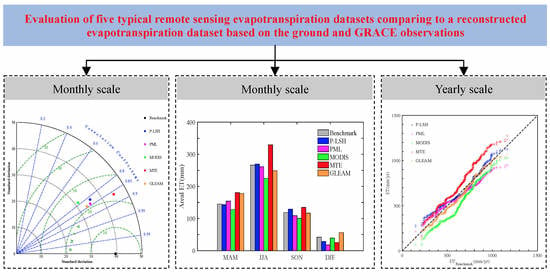
3.1. Evaluation of Yearly Scale ET Data

We first compared yearly P-LSH, PML, MODIS, MTE, and GLEAM data with yearly Recon data. All the R-values were equal to or higher than 0.85 (Figure 2). MTE had the largest R-value (0.91), followed by PML (0.88), GLEAM (0.88), P-LSH (0.86), and MODIS (0.85). Furthermore, the RMSE values of the five remote sensing ET datasets fell between 106 mm/year and 159 mm/year (Figure 2). MODIS had the largest RMSE value of 158.90 mm/year, while GLEAM had the lowest RMSE value of 106.10 mm/year (Figure 2c,e). PML (108.97 mm/year), P-LSH (114.44 mm/year) and MTE (141.32 mm/year) demonstrated an intermediate performance in terms of RMSE (Figure 2a,b,d). Furthermore, the RMSE values of PML, GLEAM and P-LSH were close (Figure 2 a,b,e), whereas the RMSE value of MODIS was more than 44 mm/year higher than that of GLEAM, PML and P-LSH (Figure 2a–c,e). In addition, the bias values of the five remote sensing ET datasets ranged between 99.45 mm/year and −106.71 mm/year (Figure 2). MODIS presented the largest bias value of −106.71 mm/year, while PML had the smallest bias value of −17.73 mm/year (Figure 2b,c). The bias value for P-LSH was 22.94 mm/year, which was close to that of PML (Figure 2a,b). Future studies should aim to reduce the bias of the MODIS and MTE algorithms.
These results confirm the above findings showing that MTE had a superior R-value, whereas GLEAM, PML and P-LSH had the advantage in terms of RMSE and bias values (Figure 2). The MTE algorithm, based on machine leaning, achieved the highest R-value, while the GLEAM, P-LSH and PML algorithms, based on physical processes, had smaller bias and RMSE values, demonstrating that the combination of intelligent algorithms (e.g., machine learning algorithms) and physical process algorithms can be applied to improve the accuracy of ET datasets and develop new ET estimation algorithms. Despite being based on physical processes, the MODIS algorithm does not use flux tower data to calibrate the model.
Figure 3 shows the spatial pattern of multiyear average annual ET across CONUS. A spatial gradient is clearly visible in the maps from west to east, and the five ET datasets across the 592 watersheds showed similar spatial gradients (Figure 3). The average annual ET gradually increased from the southwest region to the southeast and northeast regions (Figure 3). The spatial distributions of P-LSH, PML, and GLEAM were remarkably similar to that of Recon (Figure 3a–c,f). Compared with Recon, the spatial distribution of MODIS was relatively smaller in all of the western watersheds from 105° W to 120° W (Figure 3a,d), indicating why the averaged value of MODIS was smallest (Figure 4). MTE exhibited greater spatial distribution than Recon in the southeast watersheds (Figure 3a,e). The average annual ET reached its highest value in the southeast region (Figure 3).
The largest average annual ET values obtained using Recon, P-LSH, PML, MODIS, MTE, and GLEAM were 1164.86, 1131.57, 952.76, 1032.80, 1273.35, and 1065.00 mm/year, respectively (Figure 4). The southwest region showed extremely low ET (Figure 3), with values of 149.46, 269.69, 216.83, 70.05, 146.79, and 131.04 mm/year, respectively (Figure 4). The averaged value of P-LSH was closest to that of Recon, followed by PML, GLEAM, MTE, and MODIS (Figure 4), illustrating the superior accuracy of P-LSH across the whole range.
Table 2 shows the statistical metrics (bias, RMSE, and R) of the average annual ET. The results are similar to those on the yearly scale (Figure 2), whereby the R-value of MTE was the largest. The results for P-LSH were close to those for PML and GLEAM, with smaller RMSE and bias values than MODIS and MTE.

3.2. Evaluation of Seasonal-Scale ET Data

Figure 5 shows the spatial distributions of seasonal average ET data from Recon, P-LSH, PML, MODIS, MTE, and GLEAM. The seasonal variability of the five remote sensing ET datasets was consistent with that of Recon. Summer (JJA) demonstrated the largest value, followed by spring (MAM), autumn (SON), and winter (DJF) (Figure 5a–x). It is clear that the ET in spring, summer, and autumn presented a spatial gradient from west to east, especially in summer. The spatial distributions of P-LSH, PML, and GLEAM in spring, summer, and autumn were close to that of Recon. The spatial distribution of MTE in summer in the eastern region, including the North Central, Ohio, Northeast, Middle Atlantic, Lower Mississippi, and Southeast regions, was higher than that of Recon, especially in the Southeast region. In contrast, the spatial distribution of MODIS was lower in the western region, especially in Colorado Basin. It is worth noting that the winter ET of Recon, P-LSH, PML, MODIS, MTE, and GLEAM presented low values with almost no spatial variability across CONUS (Figure 5d,h,l,p,t,x). All winter average ET values were less than 200 mm. ET showed obvious seasonal changes in most watersheds of CONUS. High values generally appeared in summer and low values generally appeared in winter. However, the seasonal variation characteristics of the different regions varied.
All ET datasets were gridded to directly compute the average areal ET. Figure 6 shows the areal ET of Recon and five remote sensing ET datasets in the four seasons. According to the areal average ET from Recon, about 47% of ET in CONUS occurred in the summer, while only 7% occurred in winter (Figure 6). Spring and autumn accounted for 25% and 21%, respectively. The areal average ET values from Recon and P-LSH (gray and blue bars in Figure 6) were similar in terms of seasonal variability and magnitude, except for winter. Similarly, about 25, 47, 23, and 5% of P-LSH ET occurred in spring, summer, autumn, and winter. All areal average ET values from P-LSH, PML, MODIS, and MTE were lower than those from Recon in winter, but the areal average ET of GLEAM is larger than Recon in winter. This may be due to the lower temperature and withered vegetation in winter, leading to poor results for remote sensing retrieval. The areal ET values from MTE were slightly higher than those from Recon in spring, summer, and autumn. A substantially large bias was identified in the MTE areal ET in the four seasons. The largest bias values for MTE occurred in spring, summer, and autumn (35.57, 63.09, and 15.87 mm, respectively). The largest bias value (24.06 mm) for PML occurred in winter. Clearly, the P-LSH data were consistent with Recon.

3.3. Evaluation of Monthly-Scale ET Data

To further evaluate the five existing remote sensing ET datasets, we used a Taylor diagram at the monthly scale to compare their performance. The Taylor diagram measured the degree of correspondence between Recon and the five remote sensing ET datasets on the basis of three statistics: the correlation coefficient, the centered root-mean-square difference (RMSD), and the standard deviation, as shown in Figure 7. The monthly Recon data from the 592 watersheds from 2003 to 2008 (42,624 data points in total) were used as the reference. In terms of the correlation coefficient and RMSD, PML (pink point in Figure 7) and GLEAM (yellow point in Figure 7) were better than P-LSH (blue point in Figure 7), MTE (red point in Figure 7), and MODIS (green point in Figure 7). In terms of standard deviation, MODIS was closest to Recon, followed by GLEAM, PML, P-LSH, and MTE (Figure 7). However, MODIS had the lowest correlation coefficient (0.78) with Recon, whereas GLEAM was the closest (Figure 7).
The quality of ET datasets can be characterized by spatial and temporal accuracy. We further compared the spatial distribution of correlation coefficients and significance levels between monthly Recon data and the five remote sensing ET datasets, as shown in Figure 8. Correlation coefficients were divided into three categories: significantly positive correlation ( R ≥ 0.5 ), positive correlation ( 0 ≤ R < 0.5 ), and negative correlation ( R < 0 ). In terms of p-value, the significance level was divided into three categories: highly significant ( p < 0.01 ), significant ( 0.01 ≤ p ≤ 0.05 ), and insignificant ( p > 0.05 ). A total of 562 watersheds for P-LSH and 586 watersheds for GLEAM had a positive correlation. About 99% of watersheds for GLEAM showed significantly positive correlations, followed by PML (97%), MTE (97%), P-LSH (95%), and MODIS (93%) (Figure 8a–e). Only six watersheds for GLEAM showed a negative correlation and located in Northwest regions (Figure 8e). Thirty watersheds for P-LSH presented a negative correlation, and they were mainly distributed in the Colorado Basin and Northwest regions (Figure 8a). Twenty PML watersheds and 18 MTE watersheds presented negative correlation, and they were mainly distributed in the Northwest region (Figure 8b,d). MODIS displayed the highest number of watersheds with negative correlation among the five remote sensing ET datasets, and they were mainly distributed in the Colorado Basin, Missouri Basin, and Northwest regions (Figure 8c).
P-LSH and MODIS presented negative correlation in the southern region of the Colorado Basin, whereas PML and MTE presented positive correlation in this region. The average annual precipitation in southern Colorado is about 400 mm, with summer precipitation accounting for 70%. Therefore, this region is relatively drought-prone, and it can be characterized as a semiarid to arid climate region. ET typically comes from soil evaporation in arid regions due to the scant precipitation and sparse vegetation under normal circumstances, leading to lower vegetation transpiration. The PML-V2 algorithm considers the restriction of precipitation on soil evaporation [42], thus improving the calculation accuracy of ET in arid regions. The MTE algorithm considers the relationship between soil moisture and ET. Reduced soil moisture was shown to be responsible for the declining ET trend since 1998 [48]. Therefore, PML and MTE displayed high correlation coefficient values in the Colorado Basin. The P-LSH and MODIS algorithms need to consider precipitation, soil moisture, and other factors affecting soil evaporation, especially mutual constraints between each element.
There was a negative correlation for five remote sensing ET datasets in the Northwest region (Figure 8a–e), demonstrating their worse performance. Thus, the benchmark is probably not reliable in the Northwest region. The unreliability may be due to the coarse resolution of GRACE satellites. The spatial resolution of GRACE satellites is 50~100km. There are 19 watersheds in the northwest, but the areas of the 19 watersheds are all less than 10,000 km2. The spatial resolution of the Recon dataset is 0.125°; as a result, it may not accurately reflect the spatial variability with only 1-3 GRACE grid cell representing each watershed. In addition, this region is located at high latitudes, where the temperature is low throughout the year and there is no or little vegetation, resulting in little ET in this region. If the benchmark is indeed reliable in the Northwest, this would indicate that the five remote sensing ET algorithms need to be improved in this region.
The numbers of watersheds with a highly significant level for the five remote sensing ET datasets were 543, 565, 538, 562, and 562 (Figure 8f–j). Thus, about 5, 4, 7, 3, and 3% of watersheds showed an insignificant level for P-LSH, PML, MODIS, MTE, and GLEAM, respectively (Figure 8f–j). Thirty-two watersheds for P-LSH were insignificantly correlated, and they were mainly distributed in the Colorado Basin, California–Nevada, and Northwest regions (Figure 8f). Twenty-one watersheds for PML and nineteen watersheds for MTE were insignificantly correlated, and they were mainly distributed in the California–Nevada and Northwest regions (Figure 8g,i). Thirty-nine watersheds for MODIS were insignificantly correlated, and they were mainly distributed in the Colorado Basin, Missouri Basin, and Northwest regions (Figure 8h). Nineteen watersheds for GLEAM were insignificantly correlated, located in the Northwest and Colorado Bain. Overall, the five remote sensing ET datasets were insignificantly correlated with Recon data in the Northwest (Figure 8). A possible reason is that the Northwest region is located at high latitudes, where it freezes all year round due to a low temperature, leading to little ET. In addition, it may be possible that the Recon data are unreliable in the Northwest. As the spatial resolution of GRACE is coarse, it may lead to inaccurate calculations of water storages in small watersheds (<10000 km2).

3.4. Overall Evaluation of Five ET Products

Using the yearly Recon (2003–2008) dataset as a reference, we compared the five remote sensing ET datasets across the 592 watersheds through a quantile plot (Figure 9). To facilitate analysis of the results, we divided the data into three segments: low-value section, middle-value section, and high-value section. The corresponding ranges were 0–600, 600–1100, and 1100–1500 mm/year. PML and P-LSH tended to overestimate ET in the low-value section (Figure 9), while PML was closest to Recon for values ranging from 400 mm/year to 600 mm/year. The data points of P-LSH were generally close to the one-to-one line in the middle- and high-value sections (Figure 9). PML tended to underestimate ET in the middle- and high-value sections (Figure 9). MTE tended to overestimate ET in all sections except for really-low values (<200 mm/year) (Figure 9). MODIS systematically underestimated ET in all sections (Figure 9). Figure 9 shows why MTE and MODIS presented large bias and RMSE values in Figure 2. The data points of GLEAM were generally close to the one-to-one line in low- and middle-value sections, but it tends to underestimate the ET values in high-value section (Figure 9). In summary, P-LSH and GLEAM were the closest to Recon in the middle-value section, while the other three remote sensing ET datasets presented various degrees of overestimation and underestimation in the low- and high-value sections. This demonstrates that these three remote sensing ET algorithms (PML, MODIS, and MTE) need to be improved in these sections.
There were 371 watersheds with an average annual ET ranging from 600 to 1100 mm/year according to Recon data in CONUS, accounting for 63% of the total (Figure 3a). The five remote sensing ET datasets identified 351, 302, 237, 376, and 327 watersheds in this ET range (Figure 3b–f). The spatial distribution of average annual P-LSH was most similar to that of Recon (Figure 3a,b). This indirectly demonstrates that P-LSH was consistent with Recon in the middle- and high-value sections (Figure 9). Few ET data points were larger than 1100 mm/year, as shown in Figure 9, which corresponds to Figure 3a showing that only two watersheds had an average annual ET of more than 1100 mm/year according to Recon data. The remote sensing datasets identified 5 (P-LSH), 0 (PML), 0 (MODIS),37 (MTE), and 0 (GLEAM) watersheds with an average annual ET higher than 1100 mm/year (Figure 3b–f), thus confirming the results showing no watershed with an average annual ET higher than 1100 mm/year according to PML, MODIS, and GLEAM in Figure 4 and Figure 9.

4. Discussion

In this study, we compared five remote sensing ET datasets with Recon data. The choice of benchmark is especially important, as it determines the reliability of the comparison result [51,56]. The main driver of uncertainty for ET comparison may stem from the use of Recon data as the benchmark. In the calculation process of Recon data, downscaling of the GRACE satellite data was involved [52]. The coarse resolution of the original GRACE satellite data may cause some uncertainty in Recon dataset in these basins with a smaller area (<10,000 km2). Accuracy of the five ET datasets is also related to many other factors, such as the forcing data (precipitation, air temperature, vapor pressure, shortwave downward radiation, longwave downward radiation, and wind speed), the accuracy of observation from the flux tower station, the density of flux tower stations, vegetation types, the ET algorithm, the parameters of each ET algorithm, and the climatological and geographical conditions of the considered region [30,39]. Previous studies have mentioned that the above-listed factors are insufficient for ET estimation [7,38]. Although the results of this study clearly demonstrate that PML, P-LSH, and GLEAM performed better on a yearly and seasonal scale (Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6), these ET algorithms still need to be improved in the future. Firstly, the drive datasets for the five remote sensing ET datasets were different. The drive dataset for P-LSH was the National Centers for Environmental Prediction (NCEP) Reanalysis daily surface meteorology [7]. GLDAS-2.1 meteorological forcing was used to drive the PML model [42]. Global Modeling and Assimilation Office (GMAO) meteorological data were used to drive the MODIS model [38,39,57]. The selection of a drive dataset can impact the accuracy of the ET algorithm. More studies on how to choose the best drive dataset should be carried out.
Secondly, as demonstrated in our results, the R-value of MTE was the largest on the yearly scale and hourly scale, while the bias and RMSE values were one of the largest among the five remote sensing ET datasets. The MTE algorithm’s good fit was based on the use of a machine-learning algorithm, but it tends to generally overestimate the ET values, leading to large bias and RMSE values. The other four algorithms were based on physical processes, whereby the P-LSH, PML, and GLEAM in particular recorded smaller bias and RMSE values. Combining artificial intelligence algorithms and physical process algorithms can be applied to achieve high-quality ET products in the future study [58].
Thirdly, the spatial distribution of the five remote sensing ET datasets presented differences in the southern Colorado Basin region, which can be characterized as arid area. Despite the P-LSH, PML, MODIS, and GLEAM algorithms all being based on physical processes, the PML and GLEAM outperformed the other two in the southern Colorado Basin. The algorithm for soil evaporation used for the P-LSH is similar to that used for MODIS [39,40,59], whereas PML-V2 considers the restriction of precipitation on soil evaporation [42,60]. The GLEAM algorithm considered multiple layers of vegetation and multiple layers of soils from the land surface to the root zone [43]. The soil layers have a depth of 0-0.05 m, 0.05-1.00 m, and 1.00-2.50 m, respectively. Soil evaporation is an important part of ET, and its accuracy directly affects the reliability of ET products. Many previous studies have developed or applied algorithms for soil evaporation [61,62]. To further improve the accuracy of soil evaporation data, algorithms accounting for or offsetting these uncertainties or limitations should be studied.

5. Conclusions

Assessing ET datasets is an integral part of ET algorithm development based on a reference. In this study, we chose the ET dataset named Recon as the benchmark, which was generated from a simple ET reconstruction method based on the principle of water balance.
Although the R-value of MTE with an annual temporal resolution was the largest, its bias and RMSE values were larger than those of P-LSH, PML, and GLEAM (Figure 2). Comprehensive consideration of the three indicators of BIAS, RMSE and R, the P-LSH, PML and GLEAM demonstrated a better performance on the yearly scale (Figure 2). The P-LSH, PML, and GLEAM were closest to Recon in terms of the spatial distribution of multiyear average annual ET, while all remote sensing ET datasets could capture spatial trends and changes from west to east (Figure 3). Regardless of the time series or spatial distribution on a yearly scale, both P-LSH and PML performed well (Figure 2, Figure 3 and Figure 4). However, the bias and RMSE of the MODIS and MTE algorithms should be improved.
A spatial gradient for spring, summer, and autumn was clearly visible, whereas the spatial distribution for winter showed no spatial variability for the five ET datasets (Figure 5). According to the results of areal ET, P-LSH was most consistent with Recon data, followed by PML, MODIS, GLEAM, and MTE (Figure 6). This confirms that P-LSH performed better on a seasonal scale; however, the five remote sensing ET datasets performed poorly in winter, especially the GLEAM tends to overestimate in winter. This may have been due to the small ET, low temperature, and low vegetation in winter.
The spatial distribution of the correlation coefficients and significance levels on a monthly scale illustrated that the PML and MTE algorithms were effective in arid regions, due to their consideration of the constraints of precipitation and soil moisture on soil evaporation. Therefore, the estimation accuracy of the P-LSH and MODIS algorithms should be improved in arid regions. The MODIS tended to underestimate ET overall, which may be because it did not use observations from flux towers to calibrate the parameters of the ET algorithm.
This study provides a reference for improving the quality of ET datasets and ET estimation algorithms in the future across CONUS. It will also play an important role in promoting the application of remote sensing in ET estimation. Various ET algorithms have been proposed and implemented on a global scale. However, the practicability of each algorithm varies across regions. Future research should focus on how to combine the advantages of multiple algorithms to estimate ET and obtain high-quality ET products.

Author Contributions

L.C. and K.Z. conceptualized and designed the study, and conducted the simulations; J.F. analyzed the data; J.W. and M.Z. reviewed the manuscript. All authors discussed and reviewed this paper. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported by the National Natural Science Foundation of China (52009028 and 51879067), the National Key Research and Development Program of China (2018YFC1508101), the China Postdoctoral Science Foundation (2020M671323), the Natural Science Foundation of Jiangsu Province (BK20180022), Six Talent Peaks Project in Jiangsu Province (NY-004), and the Fundamental Research Funds for the Central Universities of China (B210202115 and B200204038).

Data Availability Statement

(1) P-LSH: http://www.ntsg.umt.edu/project/global-et.php; (2) PML: https://data.tpdc.ac.cn/; (3) MODIS: https://e4ftl01.cr.usgs.gov/MOLT/; (4) MTE: http://www.fluxcom.org/EF-Download/; (5) GLEAM: https://www.gleam.eu/#datasets.

Conflicts of Interest

The authors declare no conflict of interest. The sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Xiong, Y.J.; Zhao, S.H.; Tian, F.; Qiu, G.Y. An evapotranspiration product for arid regions based on the three-temperature model and thermal remote sensing. J. Hydrol. 2015, 530, 392–404. [Google Scholar] [CrossRef]
  2. Shen, Y.; Li, S.; Chen, Y.; Qi, Y.; Zhang, S. Estimation of regional irrigation water requirement and water supply risk in the arid region of Northwestern China 1989–2010. Agric. Water Manag. 2013, 128, 55–64. [Google Scholar] [CrossRef]
  3. Rosenfeld, D. Aerosol-Cloud Interactions Control of Earth Radiation and Latent Heat Release Budgets. Space Sci. Rev. 2007, 125, 149–157. [Google Scholar] [CrossRef]
  4. Wang, W.; Lee, X.; Xiao, W.; Liu, S.; Schultz, N.; Wang, Y.; Zhang, M.; Zhao, L. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nat. Geosci. 2018, 11, 410–414. [Google Scholar] [CrossRef]
  5. Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]
  6. Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
  7. Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res. 2010, 46, 1–21. [Google Scholar] [CrossRef] [Green Version]
  8. Allen, R.G.; Clemmens, A.J.; Burt, C.M.; Solomon, K.; O’Halloran, T. Prediction Accuracy for Projectwide Evapotranspiration Using Crop Coefficients and Reference Evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 24–36. [Google Scholar] [CrossRef] [Green Version]
  9. Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s global energy budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
  10. Teuling, A.J.; Hirschi, M.; Ohmura, A.; Wild, M.; Reichstein, M.; Ciais, P.; Buchmann, N.; Ammann, C.; Montagnani, L.; Richardson, A.D.; et al. A regional perspective on trends in continental evaporation. Geophys. Res. Lett. 2009, 36, 36. [Google Scholar] [CrossRef] [Green Version]
  11. Orth, R.; Destouni, G. Drought reduces blue-water fluxes more strongly than green-water fluxes in Europe. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef]
  12. Oberg, J.W.; Melesss, A.M. Evapotranspiration Dynamics at an Ecohydrological Restoration Site: An Energy Balance and Remote Sensing Approach. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 565–582. [Google Scholar] [CrossRef]
  13. Rana, G.; Katerji, N.; Perniola, M. Evapotranspiration of sweet sorghum: A general model and multilocal validity in semiarid environmental conditions. Water Resour. Res. 2001, 37, 3237–3246. [Google Scholar] [CrossRef]
  14. Wang, L.; Caylor, K.K.; Villegas, J.C.; Barron-Gafford, G.A.; Breshears, D.D.; Huxman, T.E. Partitioning evapotranspiration across gradients of woody plant cover: Assessment of a stable isotope technique. Geophys. Res. Lett. 2010, 37, 1–7. [Google Scholar] [CrossRef] [Green Version]
  15. Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
  16. Ruhoff, A.L.; Paz, A.R.; Aragao, L.E.O.C.; Mu, Q.; Malhi, Y.; Collischonn, W.; Rocha, H.R.; Running, S.W. Assessment of the MODIS global evapotranspiration algorithm using eddy covariance measurements and hydrological modelling in the Rio Grande basin. Hydrol. Sci. J. 2013, 58, 1658–1676. [Google Scholar] [CrossRef]
  17. Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; Van Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; Van Gorsel, E.; Knohl, A.; Law, B.E.; et al. Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef] [Green Version]
  18. Thakur, J.K.; Singh, S.K.; Ekanthalu, V.S. Integrating remote sensing, geographic information systems and global positioning system techniques with hydrological modeling. Appl. Water Sci. 2017, 7, 1595–1608. [Google Scholar] [CrossRef] [Green Version]
  19. Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Er-Raki, S.; Bigeard, G.; Merlin, O.; Garatuzapayan, J.; et al. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef] [Green Version]
  20. Wang, K.; Wang, P.; Li, Z.; Cribb, M.; Sparrow, M. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. J. Geophys. Res. Space Phys. 2007, 112, 1–14. [Google Scholar] [CrossRef]
  21. Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A Coupled Remote Sensing and Simplified Surface Energy Balance Approach to Estimate Actual Evapotranspiration from Irrigated Fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef] [Green Version]
  22. Gokmen, M.; Vekerdy, Z.; Verhoef, A.; Verhoef, W.; Batelaan, O.; Van Der Tol, C. Integration of soil moisture in SEBS for improving evapotranspiration estimation under water stress conditions. Remote Sens. Environ. 2012, 121, 261–274. [Google Scholar] [CrossRef]
  23. Shuttleworth, W.J.; Wallace, J. Evaporation from sparse crops-an energy combination theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
  24. Dickinson, R.E. Land Surface Processes and Climate—Surface Albedos and Energy Balance. In Advances in Geophysics; Elsevier BV: Amsterdam, The Netherlands, 1983; Volume 25, pp. 305–353. [Google Scholar]
  25. Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
  26. Van Der Kwast, J.; Timmermans, W.; Gieske, A.; Su, Z.; Olioso, A.; Jia, L.; Elbers, J.; Karssenberg, D.; De Jong, S. Evaluation of the Surface Energy Balance System (SEBS) applied to ASTER imagery with flux-measurements at the SPARC 2004 site (Barrax, Spain). Hydrol. Earth Syst. Sci. 2009, 13, 1337–1347. [Google Scholar] [CrossRef] [Green Version]
  27. Bhattarai, N.; Shaw, S.B.; Quackenbush, L.J.; Im, J.; Niraula, R. Evaluating five remote sensing based single-source surface energy balance models for estimating daily evapotranspiration in a humid subtropical climate. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 75–86. [Google Scholar] [CrossRef]
  28. Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
  29. Reichle, R.H. Data assimilation methods in the Earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
  30. Bodesheim, P.; Jung, M.; Gans, F.; Mahecha, M.D.; Reichstein, M. Upscaled diurnal cycles of land–atmosphere fluxes: A new global half-hourly data product. Earth Syst. Sci. Data 2018, 10, 1327–1365. [Google Scholar] [CrossRef] [Green Version]
  31. Lee, X. Energy Balance, Evaporation, and Surface Temperature. In Springer Atmospheric Sciences; Springer: Berlin/Heidelberg, Germany, 2017; pp. 191–213. [Google Scholar]
  32. Song, X.; Lu, F.; Xiao, W.; Zhu, K.; Zhou, Y.; Xie, Z. Performance of 12 reference evapotranspiration estimation methods compared with the Penman-Monteith method and the potential influences in northeast China. Meteorol. Appl. 2019, 26, 83–96. [Google Scholar] [CrossRef] [Green Version]
  33. Penman, H.L. Natural evaporation from open water, bare soil and grass. In Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character; The Royal Society: London, UK, 1948; Volume 193, pp. 120–145. [Google Scholar]
  34. Monteith, J.L. Evaporation and Environment, Symposia of the Society for Experimental Biology; Cambridge University Press (CUP): Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
  35. Mallick, K.; Jarvis, A.; Fisher, J.B.; Tu, K.P.; Boegh, E.; Niyogi, D. Latent heat flux and canopy conductance based on penman–monteith, priestley–taylor equation, and bouchet’s complementary hypothesis. J. Hydrometeorol. 2013, 14, 419–442. [Google Scholar] [CrossRef]
  36. Vanella, D.; Ramírez-Cuesta, J.M.; Intrigliolo, D.S.; Consoli, S. Combining Electrical Resistivity Tomography and Satellite Images for Improving Evapotranspiration Estimates of Citrus Orchards. Remote Sens. 2019, 11, 373. [Google Scholar] [CrossRef] [Green Version]
  37. Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
  38. Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
  39. Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
  40. Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W.; Hong, Y.; Gourley, J.J.; Yu, Z. Vegetation Greening and Climate Change Promote Multidecadal Rises of Global Land Evapotranspiration. Sci. Rep. 2015, 5, 15956. [Google Scholar] [CrossRef] [PubMed]
  41. Leuning, R.; Zhang, Y.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, 44. [Google Scholar] [CrossRef]
  42. Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.; McVicar, T.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
  43. Miralles, D.G.; Holmes, T.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
  44. Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.M.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
  45. Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosciences 2009, 6, 2001–2013. [Google Scholar] [CrossRef] [Green Version]
  46. Granata, F.; Gargano, R.; de Marinis, G. Artificial intelligence based approaches to evaluate actual evapotranspiration in wetlands. Sci. Total Environ. 2020, 703, 135653. [Google Scholar] [CrossRef]
  47. Tikhamarine, Y.; Malik, A.; Souag-Gamane, D.; Kisi, O. Artificial intelligence models versus empirical equations for modeling monthly reference evapotranspiration. Environ. Sci. Pollut. Res. 2020, 27, 30001–30019. [Google Scholar] [CrossRef]
  48. Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef] [PubMed]
  49. Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
  50. Du, T.; Yuan, G.; Wang, L.; Sun, X.; Sun, R. Comparison of Remotely Sensed Evapotranspiration Models Over Two Typical Sites in an Arid Riparian Ecosystem of Northwestern China. Remote Sens. 2020, 12, 1434. [Google Scholar] [CrossRef]
  51. Schwalm, C.R.; Huntinzger, D.N.; Michalak, A.M.; Fisher, J.; Kimball, J.S.; Mueller, B.; Zhang, K.; Zhang, Y. Sensitivity of inferred climate model skill to evaluation decisions: A case study using CMIP5 evapotranspiration. Environ. Res. Lett. 2013, 8, 024028. [Google Scholar] [CrossRef]
  52. Wan, Z.; Zhang, K.; Xue, X.; Hong, Z.; Hong, Y.; Gourley, J.J. Water balance-based actual evapotranspiration reconstruction from ground and satellite observations over the conterminous United States. Water Resour. Res. 2015, 51, 6485–6499. [Google Scholar] [CrossRef]
  53. Jiao, W.; Zhang, L.; Chang, Q.; Fu, D.; Cen, Y.; Tong, Q. Evaluating an Enhanced Vegetation Condition Index (VCI) Based on VIUPD for Drought Monitoring in the Continental United States. Remote Sens. 2016, 8, 224. [Google Scholar] [CrossRef] [Green Version]
  54. Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef] [Green Version]
  55. Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
  56. Mueller, B.; Hirschi, M.; Jimenez, C.; Ciais, P.; Dirmeyer, P.A.; Dolman, A.J.; Fisher, J.B.; Jung, M.; Ludwig, F.; Maignan, F. Benchmark products for land evapotranspiration: Landflux-eval multi-data set synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 3707–3720. [Google Scholar] [CrossRef] [Green Version]
  57. Mu, Q.; Zhao, M.; Heinsch, F.A.; Liu, M.; Tian, H.; Running, S.W. Evaluating water stress controls on primary production in biogeochemical and remote sensing based models. J. Geophys. Res. Space Phys. 2007, 112, 112. [Google Scholar] [CrossRef] [Green Version]
  58. Chia, M.Y.; Huang, Y.F.; Koo, C.H.; Fung, K.F. Recent Advances in Evapotranspiration Estimation Using Artificial Intelligence Approaches with a Focus on Hybridization Techniques—A Review. Agronony 2020, 10, 101. [Google Scholar] [CrossRef] [Green Version]
  59. Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol. 2009, 379, 92–110. [Google Scholar] [CrossRef]
  60. Zhang, Y.; Chiew, F.H.S.; Peña-Arancibia, J.; Sun, F.; Li, H.; Leuning, R. Global variation of transpiration and soil evaporation and the role of their major climate drivers. J. Geophys. Res. Atmos. 2017, 122, 6868–6881. [Google Scholar] [CrossRef]
  61. Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in Soil Evaporation Physics-A Review. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
  62. Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
Remotesensing 13 02414 g001 550
Figure 1. Map of the study area and location of 592 watersheds.
Figure 1. Map of the study area and location of 592 watersheds.
Remotesensing 13 02414 g001
Remotesensing 13 02414 g002 550
Figure 2. Yearly scale comparison of (a) P-LSH, (b) PML, (c) MODIS, (d) MTE, and (e) GLEAM data to Recon data.
Figure 2. Yearly scale comparison of (a) P-LSH, (b) PML, (c) MODIS, (d) MTE, and (e) GLEAM data to Recon data.
Remotesensing 13 02414 g002
Remotesensing 13 02414 g003 550
Figure 3. Maps of multiyear (2003–2008) average annual ET in this study: (a) Recon, (b) P-LSH, (c) PML, (d) MODIS, (e) MTE, and (f) GLEAM .
Figure 3. Maps of multiyear (2003–2008) average annual ET in this study: (a) Recon, (b) P-LSH, (c) PML, (d) MODIS, (e) MTE, and (f) GLEAM .
Remotesensing 13 02414 g003
Remotesensing 13 02414 g004 550
Figure 4. Box plot of multiyear (2003–2008) average annual ET in this study.
Figure 4. Box plot of multiyear (2003–2008) average annual ET in this study.
Remotesensing 13 02414 g004
Remotesensing 13 02414 g005 550
Figure 5. The spatial distributions of multiyear (2003–2008) mean seasonal ET for five datasets in CONUS: (a–d) spring (March, April, and May (MAM)), summer (June, July, and August (JJA)), autumn (Septemeber, October, and November (SON)), and winter (December, January, and Feburary (DJF)) average ET of Recon; (e–h) MAM, JJA, SON, and DJF average ET of P-LSH; (i–l) MAM, JJA, SON, and DJF average ET of PML; (m–p) MAM, JJA, SON, and DJF average ET of MODIS; (q–t) MAM, JJA, SON, and DJF average ET of MTE; and (u–x) MAM, JJA, SON, and DJF average ET of GLEAM.
Figure 5. The spatial distributions of multiyear (2003–2008) mean seasonal ET for five datasets in CONUS: (a–d) spring (March, April, and May (MAM)), summer (June, July, and August (JJA)), autumn (Septemeber, October, and November (SON)), and winter (December, January, and Feburary (DJF)) average ET of Recon; (e–h) MAM, JJA, SON, and DJF average ET of P-LSH; (i–l) MAM, JJA, SON, and DJF average ET of PML; (m–p) MAM, JJA, SON, and DJF average ET of MODIS; (q–t) MAM, JJA, SON, and DJF average ET of MTE; and (u–x) MAM, JJA, SON, and DJF average ET of GLEAM.
Remotesensing 13 02414 g005
Remotesensing 13 02414 g006 550
Figure 6. Comparison of regional average ET derived from Recon, P-LSH, PML, MODIS, MTE, and GLEAM.
Figure 6. Comparison of regional average ET derived from Recon, P-LSH, PML, MODIS, MTE, and GLEAM.
Remotesensing 13 02414 g006
Remotesensing 13 02414 g007 550
Figure 7. Taylor diagram of monthly P-LSH, PML, MODIS, MTE, and GLEAM data based on comparison with monthly Recon for all grid cells from 2003 to 2008.
Figure 7. Taylor diagram of monthly P-LSH, PML, MODIS, MTE, and GLEAM data based on comparison with monthly Recon for all grid cells from 2003 to 2008.
Remotesensing 13 02414 g007
Remotesensing 13 02414 g008 550
Figure 8. Spatial maps of correlation coefficients (a–e) between monthly Recon and five monthly remote sensing ET datasets and their significance levels (f–j) in this study.
Figure 8. Spatial maps of correlation coefficients (a–e) between monthly Recon and five monthly remote sensing ET datasets and their significance levels (f–j) in this study.
Remotesensing 13 02414 g008
Remotesensing 13 02414 g009 550
Figure 9. Quantile–quantile plot of Recon data vs. five remote sensing ET datasets for all watersheds.
Figure 9. Quantile–quantile plot of Recon data vs. five remote sensing ET datasets for all watersheds.
Remotesensing 13 02414 g009
Table
Table 1. Descriptions of the ET datasets used in this study, including their temporal coverages, temporal resolutions, spatial resolutions, algorithms, key equations, limitations, and references.
Table 1. Descriptions of the ET datasets used in this study, including their temporal coverages, temporal resolutions, spatial resolutions, algorithms, key equations, limitations, and references.
NameAcronymsTemporal CoverageResolutionAlgorithmKey EquationsLimitationsReferences
Actual
evapotranspiration
reconstruction		ReconApril 2002 to September 2013Monthly,
0.125°		Simple water balance E T = P − R − Δ S + ε   R i = ( Q i − ∑ n = 1 N Q T ) × T A i × 1000
Δ S m = S i ′ ( d m ) − S i ′ ( d m − 1 )   E T ¯ = 1 M ∑ m = 1 M E T m 		The resolution of Grace satellite is coarse, and the accuracy of ET in small watershed is affected.Wan et al. (2015)
Process-based land surface
evapotranspiration/heat flux		P-LSHJanuary 1982 to December 2013Monthly,
0.5°		Modified Penman-Monteith λ E s o i l = R H ( V P D / k ) Δ A s o i l + ρ C p V P D g a Δ + γ × g a / g t o t c   λ E w a t e r = α Δ A Δ + γ No considered canopy interceptionK. Zhang et al. (2015)
Penman–Monteith–LeuningPMLJuly 2002 to August 20198 day,
500 m		Modified Penman-Monteith-Leuning E t = ε A c + ( ρ c p / γ ) D a G a ε + 1 + G a / G c   E s = f ϵ A s ε + 1 Soil evaporation simplifies the physical process.Y Q. Zhang et al. (2019)
Moderate-resolution imaging
spectroradiometer		MODISJanuary 2000 to Present8 day,
500 m		Penman-Monteith-Leuning λ E w e t _ c = ( s × A C × F C + ρ × C p × ( e s a t − e ) × F C / r h r c ) × F w e t s + P a × C p × r v c λ × ε × r h r c
λ E t r a n s = ( s × A C × F C + ρ × C p × ( e s a t − e ) × F C / r a ) × ( 1 − F w e t ) s + γ × ( 1 + r s / r a )
λ E S O I L = λ E w e t _ S O I L + λ E S O I L p o r × ( R H 100 ) V P D / β 		Biome Properties Look-Up Table is an empirical value. Unused flux tower data calibration parameters.Mu et al. (2011)
Model tree ensembleMTEJanuary 1982 to December 2008Monthly,
0.5°		TRIAL + ERRORNo specific equationNo physical processJung et al. (2011)
Global land
evaporation
amsterdam model		GLEAM1980 to 2020Monthly,
0.25°		Modified Priestley-Taylor λ E P = α Δ Δ + ψ ( R n − G ) Simplified impedanceMartens et al. (2017)
Table
Table 2. Statistical metrics (Bias, RMSE, and R) of average annual ET in this study.
Table 2. Statistical metrics (Bias, RMSE, and R) of average annual ET in this study.
Five ET datasets vs. ReconBias (mm/year)RMSE (mm/year)R
P-LSH vs. Recon−22.9492.620.92
PML vs. Recon17.7383.440.93
MODIS vs. Recon-106.71145.900.89
MTE vs. Recon99.45126.390.95
GLEAM vs Recon23.1887.780.92
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Chao, L.; Zhang, K.; Wang, J.; Feng, J.; Zhang, M. A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sens. 2021, 13, 2414. https://doi.org/10.3390/rs13122414

AMA Style

Chao L, Zhang K, Wang J, Feng J, Zhang M. A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sensing. 2021; 13(12):2414. https://doi.org/10.3390/rs13122414

Chicago/Turabian Style

Chao, Lijun, Ke Zhang, Jingfeng Wang, Jin Feng, and Mengjie Zhang. 2021. "A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm" Remote Sensing 13, no. 12: 2414. https://doi.org/10.3390/rs13122414

APA Style

Chao, L., Zhang, K., Wang, J., Feng, J., & Zhang, M. (2021). A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and GRACE Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sensing, 13(12), 2414. https://doi.org/10.3390/rs13122414

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop