Water Ice Detection Research in Utopia Planitia Based on Simulation of Mars Rover Full-Polarimetric Subsurface Penetrating Radar
Abstract
:1. Introduction
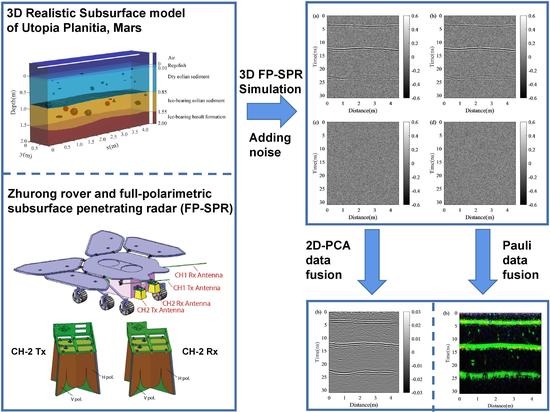
2. Establish a 3D Realistic Structure Model of Utopia Planitia
3. Simulation of the 3D Realistic Structure Model
4. Extract Effective Reflection Signal Based on 2D-PCA
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wan, W.; Wang, C.; Li, C.; Wei, Y. China’s first mission to Mars. Nat. Astron. 2020, 4, 721. [Google Scholar] [CrossRef]
- Ye, P.; Sun, Z.; Rao, W.; Meng, L. Mission overview and key technologies of the first Mars probe of China. Sci. China-Technol. Sci. 2017, 60, 649–657. [Google Scholar] [CrossRef]
- Zhou, B.; Shen, S.; Lu, W.; Liu, Q.; Tang, C.; Li, S.; Fang, G. The Mars rover subsurface penetrating radar onboard China’s Mars 2020 mission. Earth Planet Phys. 2020, 4, 345–354. [Google Scholar] [CrossRef]
- Clifford, S.; HILLEL, D. The stability of ground ice in the equatorial region of Mars. J. Geophys. Res. Solid Earth 1983, 88, 2456–2474. [Google Scholar] [CrossRef]
- Mellon, M.; Jakosky, B. The distribution and behavior of Martian ground ice during past and present epochs. J. Geophys. Res. Planet 1995, 100, 11179–11781. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zeng, Z.; Li, J.; Huang, L.; Huo, Z.; Wang, K.; Zhang, J. Parameter Estimation of Lunar Regolith from Lunar Penetrating Radar Data. Sensors 2018, 9, 2907. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Fang, G.; Feng, J.; Xing, S.; Ji, Y.; Zhou, B.; Gao, Y.; Han, L.; Dai, S.; Xiao, Y.; et al. Data processing and initial results of Chang’e–3 lunar penetrating radar. Res. Astron. Astrophys. 2014, 14, 1623–1632. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Zeng, Z.; Xu, Y.; Liu, C.; Chen, S. Stratigraphy of the Von Kármán crater based on Chang’E-4 lunar penetrating radar data. Geophys. Res. Lett. 2020, 47, e2020GL088680. [Google Scholar]
- Pei, J.; Huang, Y.; Huo, W.; Wu, J.; Yang, J.; Yang, H. SAR imagery feature extraction using 2DPCA–based two–dimensional neighborhood virtual points discriminant embedding. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 2206–2214. [Google Scholar] [CrossRef]
- Tanaka, K.; Robbins, S.; Fortezzo, C.; Skinner, J.; Hare, T. The digital global geologic map of Mars: Chronostratigraphic ages, topographic and crater morphologic characteristics, and updated resurfacing history. Planet Space Sci. 2014, 95, 11–24. [Google Scholar] [CrossRef]
- Meng, X.; Xu, Y.; Xiao, L.; Xiao, Z. Permittivity estimation of subsurface deposits in the Elysium–utopia region on Mars with MRO shallow radar sounder data. Astron. J. 2020, 159, 156. [Google Scholar] [CrossRef]
- Kreslavsky, M.; Head, J. Mars: Nature and evolution of young latitude–dependent water–ice–rich mantle. Geophys. Res. Lett. 2002, 29, 1719. [Google Scholar] [CrossRef] [Green Version]
- Smith, I.; Putzig, N.; Holt, J.; Phillips, R. An Ice Age recorded in the polar deposits of Mars. Science 2016, 352, 1075–1078. [Google Scholar] [CrossRef] [Green Version]
- Costard, F.; Sejourne, A.; Kargel, J.; Godin, E. Modeling and observational occurrences of near–surface drainage in Utopia Planitia, Mars. Geomorphology 2016, 275, 80–89. [Google Scholar] [CrossRef]
- Hass, G.; Saunders, W.; Miller, J.; Dale, M. Bearded profile with avian headdress within the southeast–facing slope of an impact crater in the Utopia Planitia region of Mars. J. Space Explor. 2016, 5, 1–27. [Google Scholar]
- Leuschen, C.; Clifford, S.; Gogineni, P. Simulation of a surface–penetrating radar for Mars exploration. J. Geophys. Res. Planets 2003, 108, 8035. [Google Scholar] [CrossRef]
- Bandfield, J.; Hamilton, V.; Christensen, P. A global view of Martian surface compositions from MGS–TES. Science 2000, 287, 1626–1630. [Google Scholar] [CrossRef] [Green Version]
- Leuschen, C.; Gogineni, S.; Clifford, S.; Raney, R. Simulation and design of ground-penetrating radar for Mars exploration. In IGARRS 2001. Scanning the Present and Resolving the Future, Proceedings of IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; IEEE: Sydney, Australia, 2001. [Google Scholar]
- Jin, Y.; Fa, W.; Xu, F. Overview of the advance for Mars exploration using microwave remote sensing. Chin. J. Space Sci. 2008, 264–272. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Li, J.; Lin, J.; Hu, Y.; Wang, X.; Sun, X. Simulation of the lunar regolith and Lunar–Penetrating radar data processing. IEEE J. Sel. Top. Appl. Earth Observ. 2018, 11, 655–663. [Google Scholar] [CrossRef]
- Feng, X.; Zou, L.; Liu, C.; Lu, Q.; Liang, W.; Li, L.; Wang, S. Forward modeling for full–polarimetric ground penetrating radar. Chin. J. Geophys. Chin. Ed. 2011, 54, 349–357. [Google Scholar]
- Valérie, C.; Charlotte, C.; Dirk, P.; Philippe, C.; Stephen, M.; Hamran, S. Wisdom GPR designed for shallow and High–Resolution sounding of the Martian subsurface. Proc. IEEE 2011, 99, 824–836. [Google Scholar]
- Li, C.; Xing, S.; Lauro, S.; Su, Y.; Dai, S.; Feng, J.; Cosciotti, B. Pitfalls in GPR data interpretation: False reflectors detected in lunar radar cross sections by Chang’e–3. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1325–1335. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, D.; Frangi, A.; Yang, J. Two–dimensional PCA: A new approach to appearance–based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Feng, X.; Ding, C.; Dong, Z.; Liu, C.; Zhang, Y.; Meng, Z. Yutu-2 Radar Sounding Evidence of a Buried Crater at Chang’E-4 Landing Site. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Feng, X.; Yu, Y.; Liu, C.; Michael, F. Subsurface polarimetric migration imaging for full polarimetric ground–penetrating radar. Geophys. J. Int. 2015, 202, 1324–1338. [Google Scholar] [CrossRef] [Green Version]






| Interfaces | Types | Range of Fluctuation (m) | ||
| Regolith surface | ±0.02 | |||
| Eolian sediment (dry/icy) | ±0.03 | |||
| Ice-bearing eolian sediment/ Basalt formation | ±0.05 | |||
| Rocks & Water ice | Types | Quantity | Diameter (m) | Relative permittivity |
| Rocks | 21 | 0.05–0.35 | 3.50 | |
| Water ice | 3 | 0.10–0.30 | 3.15 | |
| Layers | Types | Depth (m) | Relative Permittivity | |
| Regolith | 0–0.10 | 2.4 | ||
| Dry eolian sediment | 0.10–0.85 | 2.8 | ||
| Ice-bearing eolian sediment | 0.85–1.55 | 5.1 | ||
| Ice-bearing basalt formation | 1.55–2.00 | 6.9 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Feng, X.; Zhou, H.; Dong, Z.; Liang, W.; Xue, C.; Li, X. Water Ice Detection Research in Utopia Planitia Based on Simulation of Mars Rover Full-Polarimetric Subsurface Penetrating Radar. Remote Sens. 2021, 13, 2685. https://doi.org/10.3390/rs13142685
Wang Y, Feng X, Zhou H, Dong Z, Liang W, Xue C, Li X. Water Ice Detection Research in Utopia Planitia Based on Simulation of Mars Rover Full-Polarimetric Subsurface Penetrating Radar. Remote Sensing. 2021; 13(14):2685. https://doi.org/10.3390/rs13142685
Chicago/Turabian StyleWang, Ying, Xuan Feng, Haoqiu Zhou, Zejun Dong, Wenjing Liang, Cewen Xue, and Xiaotian Li. 2021. "Water Ice Detection Research in Utopia Planitia Based on Simulation of Mars Rover Full-Polarimetric Subsurface Penetrating Radar" Remote Sensing 13, no. 14: 2685. https://doi.org/10.3390/rs13142685
APA StyleWang, Y., Feng, X., Zhou, H., Dong, Z., Liang, W., Xue, C., & Li, X. (2021). Water Ice Detection Research in Utopia Planitia Based on Simulation of Mars Rover Full-Polarimetric Subsurface Penetrating Radar. Remote Sensing, 13(14), 2685. https://doi.org/10.3390/rs13142685