Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Product Availability
2.2. PPP Observation Equations
2.3. Ambiguity-Float PPP Observation Model
2.4. Ambiguity-Fixed PPP Strategy
- Calculate SD ionospheric-free float ambiguity. The un-difference ionospheric-free float ambiguities with their variance-covariance matrix (VCM) are calculated from the standard EKF. The SD ionospheric-free ambiguities can be calculated by SD operation and the SD variance-covariance matrix is obtained by applying the covariance propagation law:where is the SD ionospheric-free float ambiguity with their variance de noted by . is SD design matrix and is ionospheric-free ambiguity VCM calculated by EKF. The symbol denotes this term can be eliminated with using CODE and WHU PPP AR products.
- Fix SD WL ambiguity. The SD WL ambiguities are computed from the MW combination as showing in (7), and then are corrected by the PPP AR products (WSB or WL-FCB) to recover their integer property. The fixing decision is made according to Dong and Bock [32]. Typically, a simple rounding method is used for fixing the SD WL ambiguity because of its relatively long wavelength. The SD WL ambiguities can easily be fixed after averaging over several epochs.where denotes fixed SD WL ambiguity and is averaged MW combination over several epochs. The WL UPD correction is dispensable and can be eliminated with using CODE and WHU PPP AR products.
- Fix SD NL ambiguity. After successfully fixing the WL ambiguities, the SD float narrow-lane ambiguities are derived from their relationship with the SD float ionospheric-free ambiguities and the SD-fixed WL ambiguities in (6):where variance of the SD float NL ambiguities is obtained by applying the covariance propagation law. The NL UPD correction is required for FCB method. Since NL ambiguities are strongly correlated in PPP, a search strategy based on the well-known Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method [33] or a modified version [34], Ref [35] is should to be applied to fix the SD NL ambiguities. Fixing decisions are made by the popular ratio test and the success rate.
- Fix SD ionospheric-free ambiguity. After successful fixing of the SD WL and NL ambiguities, the SD ionospheric-free ambiguities can be recalculated with integer property,Note the NL UPD correction is required for FCB method.
- Update fixed solution. The other parameters including position, ZWD, and remnant unfixed ambiguities can be updated by their correlation with the fixed ambiguities,where and are the position estimators of the fixed and float solution, respectively, is the float ambiguity vector with the VCM , is the integer ambiguity vector, and is the covariance matrix of and .
2.5. PPP Ambiguity Resolution Products for User Solution
2.5.1. WSB/IRC Products
2.5.2. WL/NL FCB Products
2.5.3. OSB/AFC Products
3. Results
3.1. Experimental Setup
3.2. Ambiguity-Float and Fixed PPP Results
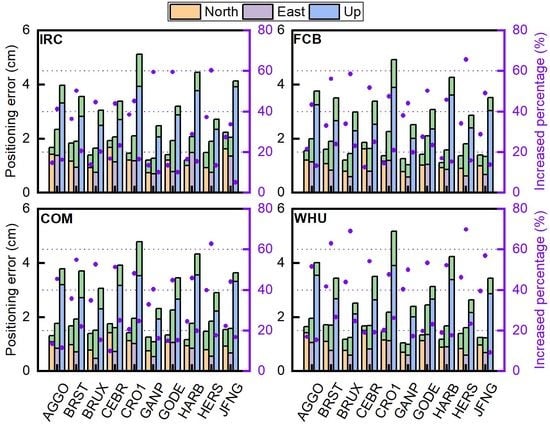
3.3. Ambiguity-Fixed Solutions from Different ACs
3.4. Benefit of Multi-GNSS Combination for PPP AR
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malys, S.; Jensen, P.A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Gao, Z.; Ge, M.; Niu, X.; Huang, L.; Tu, R.; Li, X. On the convergence of ionospheric constrained precise point positioning (IC-PPP) based on undifferential uncombined raw GNSS observations. Sensors 2013, 13, 15708–15725. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Pan, Y.; Li, X.; Guo, J.; Liu, J.; Chen, X.; Zhang, Y. Noise Characteristics of High-Rate Multi-GNSS for Subdaily Crustal Deformation Monitoring. J. Geophys. Res. Solid Earth 2018, 123, 1987–2002. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Ge, Y. Rapid displacement determination with a stand-alone multi-GNSS receiver: GPS, Beidou, GLONASS, and Galileo. GPS Solut. 2019, 23, 54. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Nilsson, T.; Ning, T.; Heinkelmann, R.; Ge, M.; Glaser, S.; Schuh, H. Real-time retrieval of precipitable water vapor from GPS and BeiDou observations. J. Geod. 2015, 89, 843–856. [Google Scholar] [CrossRef]
- Gao, Y.; Shen, X. A New Method for Carrier-Phase-Based Precise Point Positioning. Navigation 2002, 49, 109–116. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Guo, B.; Wickert, J.; Schuh, H. Temporal point positioning approach for real-time GNSS seismology using a single receiver. Geophys. Res. Lett. 2013, 40, 5677–5682. [Google Scholar] [CrossRef] [Green Version]
- Calais, E.; Han, J.; DeMets, C.; Nocquet, J. Deformation of the North American plate interior from a decade of continuous GPS measurements. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Chen, X.; Pan, Y.; Mao, S.; Li, C.; Zhou, J.; Zhang, K. PRIDE PPP-AR: An open-source software for GPS PPP ambiguity resolution. GPS Solut. 2019, 23. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Gao, Y.; Heck, B. A unified model for multi-frequency PPP ambiguity resolution and test results with Galileo and BeiDou triple-frequency observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef] [Green Version]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS ambiguity resolution using the decoupled clock model and ambiguity datum fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef] [Green Version]
- Laurichesse, D.; Mercier, F.; BERTHIAS, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. J. Navig. 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Selmke, I.; Wang, N. Estimating ambiguity fixed satellite orbit, integer clock and daily bias products for GPS L1/L2, L1/L5 and Galileo E1/E5a, E1/E5b signals. J. Geod. 2021, 95, 44. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, X.; Li, P.; Ma, F.; Pan, L. Multi-GNSS fractional cycle bias products generation for GNSS ambiguity-fixed PPP at Wuhan University. GPS Solut. 2019, 24, 15. [Google Scholar] [CrossRef]
- Li, P.; Jiang, X.; Zhang, X.; Ge, M.; Schuh, H. GPS + Galileo + BeiDou precise point positioning with triple-frequency ambiguity resolution. GPS Solut. 2020, 24, 78. [Google Scholar] [CrossRef]
- Li, X.; Han, X.; Li, X.; Liu, G.; Feng, G.; Wang, B.; Zheng, H. GREAT-UPD: An open-source software for uncalibrated phase delay estimation based on multi-GNSS and multi-frequency observations. GPS Solut. 2021, 25, 66. [Google Scholar] [CrossRef]
- Xiao, G.; Sui, L.; Heck, B.; Zeng, T.; Tian, Y. Estimating satellite phase fractional cycle biases based on Kalman filter. GPS Solut. 2018, 22, 82. [Google Scholar] [CrossRef]
- Liu, G.; Guo, F.; Wang, J.; Du, M.; Qu, L. Triple-Frequency GPS Un-Differenced and Uncombined PPP Ambiguity Resolution Using Observable-Specific Satellite Signal Biases. Remote Sens. 2020, 12, 2310. [Google Scholar] [CrossRef]
- Glaner, M.; Weber, R. PPP with integer ambiguity resolution for GPS and Galileo using satellite products from different analysis centers. GPS Solut. 2021, 25, 102. [Google Scholar] [CrossRef]
- Geng, J.; Chen, X.; Pan, Y.; Zhao, Q. A modified phase clock/bias model to improve PPP ambiguity resolution at Wuhan University. J. Geod. 2019, 93, 2053–2067. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2013, 18, 519–528. [Google Scholar] [CrossRef]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the interoperability of IGS products for precise point positioning with ambiguity resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. Available online: https://kb.igs.org/hc/en-us/articles/201271873-A-Guide-to-Using-the-IGS-Products (accessed on 12 August 2021).
- Peng, Y.; Scales, W.A.; Hartinger, M.D.; Xu, Z.; Coyle, S. Characterization of multi-scale ionospheric irregularities using ground-based and space-based GNSS observations. Satell. Navig. 2021, 2, 14. [Google Scholar] [CrossRef]
- Zhao, L.; Ye, S.; Song, J. Handling the satellite inter-frequency biases in triple-frequency observations. Adv. Space Res. 2017, 59, 2048–2057. [Google Scholar] [CrossRef]
- Liu, S.; Sun, F.; Zhang, L.; Li, W.; Zhu, X. Tight integration of ambiguity-fixed PPP and INS: Model description and initial results. GPS Solut. 2016, 20, 39–49. [Google Scholar] [CrossRef]
- Dong, D.N.; Bock, Y. Global Positioning System network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. Solid Earth 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Teunissen, P.; De Jonge, P.; Tiberius, C. The LAMBDA method for fast GPS surveying. In Proceedings of the International Symposium “GPS Technology Applications”, Bucharest, Romania, 26–29 September 1995. [Google Scholar]
- Chang, X.-W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef] [Green Version]
- Bakuła, M. Instantaneous Ambiguity Reinitialization and Fast Ambiguity Initialization for L1-L2 GPS Measurements. Sensors 2020, 20, 5730. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Zhang, X.; Ren, X.; Zuo, X.; Pan, Y. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning. GPS Solut. 2015, 20, 771–782. [Google Scholar] [CrossRef]
- Villiger, A.; Schaer, S.; Dach, R.; Prange, L.; Sušnik, A.; Jäggi, A. Determination of GNSS pseudo-absolute code biases and their long-term combination. J. Geod. 2019, 93, 1487–1500. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Guo, F. Predicting atmospheric delays for rapid ambiguity resolution in precise point positioning. Adv. Space Res. 2014, 54, 840–850. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2015, 20, 849–862. [Google Scholar] [CrossRef]
- Zhou, F.; Cao, X.; Ge, Y.; Li, W. Assessment of the positioning performance and tropospheric delay retrieval with precise point positioning using products from different analysis centers. GPS Solut. 2019, 24, 12. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef] [Green Version]










| Institution | Form | Constellation | Available |
|---|---|---|---|
| CNES (GRM) | WSB+IRC | GR*E | ftp://igs.ign.fr/pub/igs/products |
| WUM | WL/NL FCB | GR*EB2J | https://github.com/FCB-SGG |
| CODE (COM) | OSB/AFC | GR*EB2* | http://ftp.aiub.unibe.ch/CODE/ |
| PRIDE (WHU) | OSB/AFC | GR*EB2B3 | ftp://igs.gnsswhu.cn/ |
| Static | Kinematic | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Float | Fix | Float | Fix | |||||||||
| N | E | U | N | E | U | N | E | U | N | E | U | |
| GRM | 0.58 | 1.00 | 1.50 | 0.47 | 0.56 | 1.39 | 1.76 | 2.15 | 4.09 | 1.42 | 1.3 | 3.6 |
| WUM | 0.59 | 0.94 | 1.44 | 0.45 | 0.43 | 1.27 | 1.67 | 1.97 | 3.90 | 1.34 | 1.13 | 3.3 |
| COM | 0.58 | 0.90 | 1.47 | 0.47 | 0.39 | 1.32 | 1.61 | 1.94 | 3.86 | 1.28 | 1.1 | 3.3 |
| WHU | 0.59 | 0.93 | 1.51 | 0.45 | 0.42 | 1.34 | 1.67 | 2.00 | 4.01 | 1.28 | 1.07 | 3.4 |
| GRM | 0.46 | 0.75 | 1.25 | 0.37 | 0.46 | 1.13 | 1.02 | 1.39 | 3.00 | 0.85 | 0.90 | 2.71 |
| WUM | 0.48 | 0.73 | 1.21 | 0.37 | 0.35 | 1.05 | 0.92 | 1.21 | 2.80 | 0.77 | 0.68 | 2.40 |
| COM | 0.36 | 0.51 | 1.32 | 0.29 | 0.27 | 1.21 | 0.78 | 0.96 | 2.44 | 0.60 | 0.53 | 2.26 |
| WHU | 0.40 | 0.59 | 1.35 | 0.3 | 0.28 | 1.26 | 0.87 | 1.10 | 2.63 | 0.65 | 0.52 | 2.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Xiao, G.; Chang, G.; Xu, T.; Yang, L. Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers. Remote Sens. 2021, 13, 3266. https://doi.org/10.3390/rs13163266
Chen C, Xiao G, Chang G, Xu T, Yang L. Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers. Remote Sensing. 2021; 13(16):3266. https://doi.org/10.3390/rs13163266
Chicago/Turabian StyleChen, Chao, Guorui Xiao, Guobin Chang, Tianhe Xu, and Liu Yang. 2021. "Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers" Remote Sensing 13, no. 16: 3266. https://doi.org/10.3390/rs13163266
APA StyleChen, C., Xiao, G., Chang, G., Xu, T., & Yang, L. (2021). Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers. Remote Sensing, 13(16), 3266. https://doi.org/10.3390/rs13163266