Dual-Satellite Alternate Switching Ranging/INS Integrated Navigation Algorithm for Broadband LEO Constellation Independent of Altimeter and Continuous Observation

Abstract

In challenging environments such as forests, valleys and higher latitude areas, there are usually fewer than four visible satellites. For cases with only two visible satellites, we propose a dual-satellite alternate switching ranging integrated navigation algorithm based on the broadband low earth orbit (LEO) constellation, which integrates communication and navigation (ICN) technology. It is different from the traditional dual-satellite integrated navigation algorithm: the difference is that it can complete precise real-time navigation and positioning without an altimeter and continuous observation. First, we give the principle of our algorithm. Second, with the help of an unscented Kalman filter (UKF), we give the observation equation and state equation of our algorithm, and establish the mathematical model of multipath/non-line of sight (NLOS) and noise interference. Finally, based on the SpaceX constellation, for various scenarios, we analyze the performance of our algorithm through simulation. The results show that: our algorithm can effectively suppress the divergence of the inertial navigation system (INS), in the face of different multipath/NLOS interference and various noise environments it still keeps good robustness, and also has great advantages in various indicators compared with the traditional dual-satellite positioning algorithms and some existing 3-satellite advanced positioning algorithms. These results show that our algorithm can meet the real-time location service requirements in harsh and challenging environments, and provides a new navigation and positioning method when there are only two visible satellites.

1. Introduction

With the increasing demand for automatic driving and unmanned control systems, the accuracy of positioning technology must also increase in urban, indoor and valley environments. However, ground obstacles cause signal blockage and reflection, which leads to multipath interference and the difficulty of non-line-of-sight (NLOS) signal reception. At the same time, it also leads to a reduction in the number of available satellites. The positioning error caused by ground obstacles can be as high as 100 m [1], which is difficult to detect by traditional portable receivers. In this challenging environment, traditional positioning technology cannot provide accurate positioning results independently because it is difficult to guarantee the observation quality of satellite signals. China’s Beidou-1 (BDS-1) dual-satellite positioning system is a typical example: it requires the aid of an altimeter to obtain the height information required for the third observation. In addition, it needs continuous observation, which delays positioning results [2], and means that real-time performance cannot be guaranteed. Therefore, to address location service demands in challenging environments with only two visible satellites, a low-cost positioning scheme with precise real-time positioning is urgently needed.

Global coverage can be achieved with low earth orbit (LEO) constellations, due to the huge number available. The use of LEO constellations has the advantages of small path loss, short transmission delay, relatively stronger signal power and so forth. Moreover, since the rapid motion of LEO satellites enriches the geometric characteristics of the satellites and enables rapid convergence of positioning results, the real-time positioning performance of the LEO constellations is very strong, meaning that they can be used for wireless communication services, as well as navigation and positioning services [3]. Related research into broadband LEO constellations is a current research hotspot, and is developing in a similar direction as research on future navigation and positioning. While navigation and wireless communication have very similar theoretical and technical foundations, they have different emphases on signal measurement and information transmission, and therefore develop along different pathways. However, with the rapid development of autonomous driving and wireless interconnection technologies, the functions of navigation and communication have become closely related, and the necessity of their integration is being more widely acknowledged [4,5,6]. In recent years, the rapid development of large LEO constellations has provided an opportunity to solve navigation and positioning problems in challenging environments.

Several studies [7,8,9,10,11] have analyzed the feasibility of the inertial navigation system (INS)+dual satellite (INS+ dual satellite) positioning combination, and proposed possible countermeasures to issues in the application of integrated navigation on aircraft, however, these algorithms require continuous observation to complete positioning. The authors of [12] introduced the concept of similar ellipsoids and proposed a positioning solution method for the dual-satellite positioning system, deriving an accurate model of the third observation related to the user’s elevation in the dual-satellite positioning system, and then establishing the user’s positioning algorithm, however, the algorithm requires the help of an altimeter to complete navigation and positioning. In [13], a dual-satellite navigation and positioning method based on the combination of passive ranging information and a Doppler navigation system (DNS) was proposed, however, the algorithm could only complete planar navigation and positioning. For cases where only two satellites are visible, [14] proposed a positioning model that calculates the absolute position by changing the relative position. The disadvantage of this algorithm is that the anti-interference performance is poor, and it is susceptible to interference from the external environment. In [15], the authors proposed a novel user position estimation algorithm, which realized position estimation using only two satellites, however, the algorithm only considers medium earth orbit (MEO) satellites and has not been verified under the LEO constellation. Based on the measured values of the pseudorange and pseudorange rate, [16] used a Kalman filter (KF) for fusion positioning. Results of this study showed that once two satellites were tracked, the overall accuracy of the positioning system was improved, however, the algorithm is unable to meet navigation and positioning needs in harsh and challenging environments. To address navigation and positioning situations in challenging environments, [17] proposed a tightly coupled integrated navigation solution made up of an adaptive low-cost global navigation satellite system (GNSS), micro-electro-mechanical systems (MEMS) and inertial measuring units (IMU) (GNSS/MEMS-IMU), with auxiliary measurement functions, with an algorithm which requires three or more satellites to be captured in order to be implemented. The authors of [18] proposed the Marquardt algorithm with an additional Earth ellipsoid equation. Under weak GNSS signal conditions, positioning can be achieved using this method when two satellite signals are captured twice in a short period, however, the algorithm requires two captures, so real-time performance cannot be guaranteed. In [19], a single-satellite positioning scheme is proposed, based on LEO constellation clock error elimination, and detailed clock error elimination principles and methods is outlined. This algorithm has high positioning accuracy and is suitable for navigation and positioning problems in extreme and challenging environments. However, the study does not give a solution for other situations where there are insufficient visible satellites. For challenging environments such as inside buildings, under metal roofs, or underground, where only inertial or contact navigation methods can be used, [20,21,22] outline the possibility of deploying inertial navigation in wheeled mobile platforms, six-axis aircraft and trajectory control equipment, respectively. However, inertial navigation can only be used reliably when in combination with other sensors (odometer, magnetometer).

One solution to the various problems associated with the algorithms described above, is the newly proposed dual-satellite integrated navigation positioning algorithm for broadband LEO constellations, which is low-cost, robust, operates in real-time, and, as an integrated navigation system, has anti-interference abilities. It can meet real-time navigation and positioning requirements without the aid of an altimeter, continuous observation, or reliance on GNSS, and it can provide a real-time location service solution in harsh and challenging environments such as lush forests, canyons, and gullies.

In Section 2, we describe the corresponding algorithm principle and process. In Section 3, we analyze the integrated navigation and communication (ICN) algorithm of the broadband LEO constellation and give the corresponding state equation, observation equation and various error models. In Section 4, we describe the simulation and qualitative and quantitative analyses conducted with our algorithm for two common alternate switching situations. In Section 5, we give the positioning results of the algorithm under different interference environments, based on the multipath/NLOS model and noise model, to test the robustness of our algorithm. In the final section, we provide a discussion, conclusions, and suggestions for future research.

2. Algorithm Principle

Since broadband LEO satellites are communication satellites, their clock bias can be eliminated through a full-duplex (FD) communication system based on ICN technology (ICNT) [19]. Therefore, the following algorithms do not consider the error between the LEO satellite and the receiver clock, and the specific method for eliminating the clock bias is not within the scope of our article.

2.1. Standard INS+LEO-Dual Satellite (INS+LEO 2-Satellite) Integrated Navigation Algorithm

The working principle of the standard INS+LEO-dual satellite (INS+LEO2-satellite) integrated navigation algorithm is as follows. Firstly, the satellite ephemeris data provided by the LEO satellite, and the position and velocity information provided by the INS, are used to calculate the pseudorange and pseudorange rate corresponding to the INS position and velocity. In this study, the INS we use and refer to is a strapdown INS. Secondly, the measurement value of integrated navigation is taken as the difference between the pseudorange and pseudorange rate measured by the LEO satellite, and the pseudorange and pseudorange rate calculated previously. The optimal estimation of error between the LEO satellite and INS is obtained using an unscented Kalman filter (UKF). Finally, the two systems are calibrated separately. This two-way assistance method enables the standard INS+LEO2-satellite integrated navigation mode to work stably for a period, and meet the basic navigation and positioning requirements for the carrier flight. The process is depicted in a schematic diagram in Figure 1, and the corresponding principles and procedures are as follows.

According to Figure 1, assuming that the position of satellite #1 in Earth-centered Earth-fixed (ECEF) coordinates is $(x_1,y_1,z_1)$, the position of satellite #2 in ECEF coordinates is $(x_2,y_2,z_2)$, the true position of the carrier in the ECEF coordinate system is $(x_u,y_u,z_u)$, and the position calculated by INS is a known quantity $(x_I,y_I,z_I)$, ${\rho }_1$ and ${\rho }_2$ represent the true ranging values of satellites #1 and #2, respectively. ${\rho }_{I1}$ and ${\rho }_{I2}$ represent the ranging values of satellite #1 and satellite #2 obtained by the INS extrapolation solution, respectively. We derive the following equation:

$$\{\begin{array}{c}{\rho }_1=\sqrt{{(x_1-x_u)}^2+{(y_1-y_u)}^2+{(z_1-z_u)}^2}\\ {\rho }_2=\sqrt{{(x_2-x_u)}^2+{(y_2-y_u)}^2+{(z_2-z_u)}^2}\end{array}$$

(1)

and the position calculated by INS is:

$$\{\begin{array}{l}{\rho }_{I1}=\sqrt{{(x_1-x_I)}^2+{(y_1-y_I)}^2+{(z_1-z_I)}^2}\\ {\rho }_{I2}=\sqrt{{(x_2-x_I)}^2+{(y_2-y_I)}^2+{(z_2-z_I)}^2}\end{array}$$

(2)

According to Equations (1) and (2), we use the difference between ${\rho }_1$ and ${\rho }_{I1}$ and the difference between ${\rho }_2$ and ${\rho }_{I2}$ as the filtered observations, combined with the least squares (LS) algorithm or Kalman filter algorithm, to obtain the three-dimensional position solution.

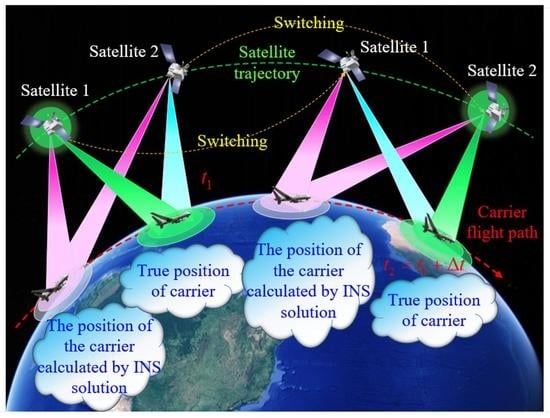
2.2. INS+LEO2-Satellite Alternate Switching Ranging Integrated Navigation Algorithm

2.2.1. Algorithm Principle

Two LEO satellites visible at any time of the carrier’s flight position are chosen and named satellites #1 and #2. Unlike the traditional dual-satellite combination algorithm, our algorithm only has the true ranging value of one satellite at any time during the carrier’s flight. However, there are two satellites’ ranging values participating in INS integrated navigation filtering: one is the satellite’s true ranging value, and the other is the virtual ranging value of the satellite. The real ranging value is the distance from the current satellite position calculated by the satellite ephemeris to the real position of the carrier. The virtual ranging value is the distance from the current satellite position calculated by the satellite ephemeris, to the current carrier position from real-time measurement by INS. The real range value and the virtual range value are alternately changed at alternating time intervals to realize the INS+LEO2-satellite alternate switching ranging integrated navigation and positioning.

2.2.2. Algorithm Flow

We assume that the real-time carrier coordinates measured by the INS in the ECEF coordinate system are $({\widehat{x}}_u,{\widehat{y}}_u,{\widehat{z}}_u)$, which is a known quantity. ${\widehat{\rho }}_1$ and ${\widehat{\rho }}_2$ represent the virtual ranging values of satellites #1 and #2 measured by INS, respectively, the alternate interval is Δt, and other parameters are the same as the standard INS+LEO2-satellite integrated navigation algorithm. The corresponding working principle diagram is shown in Figure 2.

At time $t_1$, using the real ranging value ${\rho }_1$ of satellite #1, and the virtual ranging value ${\widehat{\rho }}_2$ of satellite #2, the following expressions are obtained:

$$\{\begin{array}{c}{\rho }_1=\sqrt{{(x_1-x_u)}^2+{(y_1-y_u)}^2+{(z_1-z_u)}^2}\\ {\widehat{\rho }}_2=\sqrt{{(x_2-{\widehat{x}}_u)}^2+{(y_2-{\widehat{y}}_u)}^2+{(z_2-{\widehat{z}}_u)}^2}\end{array}$$

(3)

At this time, according to Equations (2) and (3), we use the difference between ${\rho }_1$ and ${\rho }_{I1}$ and the difference between ${\widehat{\rho }}_2$ and ${\rho }_{I2}$ as the filter’s observations.

At time $t_2=t_1+\Delta t$, using the virtual ranging value ${\widehat{\rho }}_1$ of satellite #1 and the real ranging value ${\rho }_2$ of satellite #2, the following expressions are obtained:

$$\{\begin{array}{c}{\widehat{\rho }}_1=\sqrt{{(x_1-{\widehat{x}}_u)}^2+{(y_1-{\widehat{y}}_u)}^2+{(z_1-{\widehat{z}}_u)}^2}\\ {\rho }_2=\sqrt{{(x_2-x_u)}^2+{(y_2-y_u)}^2+{(z_2-z_u)}^2}\end{array}$$

(4)

At this time, according to Equations (2) and (4), we use the difference between ${\widehat{\rho }}_1$ and ${\rho }_{I1}$ and the difference between ${\rho }_2$ and ${\rho }_{I2}$ as the filter’s observations.

We then loop through this process, at every $\Delta t$ time alternating switching the real ranging value and virtual ranging value of the satellite, straight to the end of flight time.

3. Analysis of Dual-Satellite Alternate Switching Ranging/INS Integrated Navigation Algorithm for Broadband LEO Constellations

3.1. State Equation

We combine the attitude error, velocity error, and position error of the INS with the first-order Markov drift of the gyroscope and the first-order Markov offset of the accelerometer. Here, due to the limited space, we only list the related equations and omit the tedious deduction process; the detailed process can be found in [23,24]. We take the navigation coordinate system as the geographic coordinate system, and we can obtain the state variables as follows:

$$X_S={[{\phi }_E,{\phi }_N,{\phi }_U,\delta V_E,\delta V_N,\delta V_U,\delta L,\delta \lambda ,\delta h,{\xi }_E,{\xi }_N,{\xi }_U,{\nabla }_E,{\nabla }_N,{\nabla }_U]}^T$$

(5)

where E, N and U represent the east, north and up directions of the local Cartesian coordinate system (ENU coordinate system), respectively; ${\phi }_E$, ${\phi }_N$ and ${\phi }_U$ represent the roll angle, pitch angle and yaw angle of the carrier, respectively; and $\delta L$, $\delta \lambda$ and $\delta h$ represent the latitude, longitude and altitude errors of the carrier, respectively. $\delta V_i$ represents the velocity error in all directions; ${\xi }_i$ is the first-order Markov drift of the gyroscope in the carrier coordinate system; ${\nabla }_i$ is the first-order Markov offset of the accelerometer, and $i=E,N,U$.

3.1.1. The State Equation of INS

The error state equation of INS is as follows [19]:

$${\dot{X}}_S(t)=F_{IS}(t)X_S(t)+G_S(t)W_S(t)$$

(6)

where the state variable $X_S(t)$ is shown in Equation (5), and the expression of the process noise vector is as follows:

$$W_S(t)={[{\sigma }_{bx},{\sigma }_{by},{\sigma }_{bz},{\sigma }_{ax},{\sigma }_{ay},{\sigma }_{az}]}^T$$

(7)

where ${\sigma }_{ax}$, ${\sigma }_{ay}$, and ${\sigma }_{az}$ are the random offset noise of the accelerometer in the E, N and U direction, and σ_bx, ${\sigma }_{by}$, and ${\sigma }_{bz}$ are the random drift noise of the gyroscope in the E, N and U direction.

$F_S(t)\in {\Re }^{15\times 15}$ is the state transition matrix. $G_S(t)\in {\Re }^{15\times 6}$ is the noise driving matrix, and the expression is as follows:

$$G_S(t)={\left[\begin{array}{ll}{C}_b^n\hfill & O_{3\times 3}\hfill \\ O_{3\times 3}\hfill & C_b^n\hfill \\ I_{3\times 3}\hfill & O_{3\times 3}\hfill \\ I_{3\times 3}\hfill & O_{3\times 3}\hfill \\ O_{3\times 3}\hfill & I_{3\times 3}\hfill \end{array}\right]}_{15\times 6}$$

(8)

where $C_b^n$ is the coordinate conversion matrix, with its specific expression given later; $X = X_S$; $F = F_S$; $G = G_S$; $W = W_S$.

3.1.2. The State Equation of GNSS

The random error model of the GNSS system can be described as [25]:

$$\{\begin{array}{c}\delta {\dot{t}}_u=\delta t_{ru}+w_{tu}\\ \delta {\dot{t}}_{ru}=-{\beta }_{tru}\delta t_{ru}+w_{tru}\end{array}$$

(9)

where $\delta t_u$ is the equivalent distance error of the clock offset, $\delta t_{ru}$ is the equivalent distance error of the clock drift of the first-order Markov process, $\delta {\dot{t}}_u$ and $\delta {\dot{t}}_{ru}$ are the corresponding differential, $w_{tu}$ and $w_{tru}$ are Gaussian white noise with a mean value of 0, ${\beta }_{tru}=\frac{1}{{\tau }_r}$ is the anti-correlation time, and ${\tau }_r$ is the correlation time.

The state equation of the GNSS system can be described as [19]:

$${\dot{X}}_G(t)=F_G(t)X_G(t)+G_G(t)W_G(t)$$

(10)

where $F_G(t)=\left[\begin{array}{cc}1& 0\\ 0& -{\beta }_{tru}\end{array}\right]$, $X_G(t)={\left[\begin{array}{cc}\delta t_u& \delta t_{ru}\end{array}\right]}^T$, $G_G(t)=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$, $W_G(t)=\left[\begin{array}{c}{w}_{tu}\\ w_{tru}\end{array}\right]$. According to our hypothesis, $\delta t_u$ and $\delta t_{ru}$ can be eliminated by the FD system, so $X_G(t)={\left[\begin{array}{cc}0& 0\end{array}\right]}^T$, and Equation (10) becomes:

$${\dot{X}}_G(t)=G_G(t)W_G(t)$$

(11)

Combining Equations (6), (10) and (11), we can obtain the state equation of the combined system as:

$$\left[\begin{array}{c}{\dot{X}}_S(t)\\ {\dot{X}}_G(t)\end{array}\right]=\left[\begin{array}{cc}{F}_S(t)& 0\\ 0& F_G(t)\end{array}\right]\left[\begin{array}{c}{X}_S(t)\\ X_G(t)\end{array}\right]+\left[\begin{array}{cc}{G}_S(t)& 0\\ 0& G_G(t)\end{array}\right]\left[\begin{array}{c}{W}_S(t)\\ W_G(t)\end{array}\right]$$

(12)

3.2. Observation Equation

In the ECEF coordinate system, let ${(x_s,y_s,z_s)}^T$ be the satellite position obtained by GNSS ephemeris. The corresponding pseudorange solved by INS is:

$${\rho }_k=\sqrt{{(x_I-x_s^k)}^2+{(y_I-y_s^k)}^2+{(y_I-y_s^k)}^2}$$

(13)

where $k$ is the $k$-th satellite.

Assuming that the real coordinate position of the INS position is (x,y,z), the observation equation of the pseudorange difference between INS and GNSS is [26]:

$$\delta {\rho }_k=\frac{\partial {\rho }_k}{\partial x}\delta x+\frac{\partial {\rho }_k}{\partial y}\delta y+\frac{\partial {\rho }_k}{\partial z}\delta z-v_{\rho k}$$

(14)

in the Formula (14), $v_{\rho k}$ represents the pseudorange measurement white noise of the k-th satellite $S_k$, and the first three terms of Formula (14) can be expressed as:

$$\{\begin{array}{c}\frac{\partial {\rho }_k}{\partial x}=\frac{x-x_s^k}{\sqrt{{(x-x_s^k)}^2+{(y-y_s^k)}^2+{(y-y_s^k)}^2}}=\frac{x-x_s^k}{\rho }\\ \frac{\partial {\rho }_k}{\partial y}=\frac{y-x_s^k}{\sqrt{{(x-x_s^k)}^2+{(y-y_s^k)}^2+{(y-y_s^k)}^2}}=\frac{y-y_s^k}{\rho }\\ \frac{\partial {\rho }_k}{\partial z}=\frac{z-x_s^k}{\sqrt{{(x-x_s^k)}^2+{(y-y_s^k)}^2+{(y-y_s^k)}^2}}=\frac{z-z_s^k}{\rho }\end{array}$$

(15)

where $\rho =\sqrt{{(x-x_s^k)}^2+{(y-y_s^k)}^2+{(y-y_s^k)}^2}$.

Finally, the pseudorange observation equation can be obtained as:

$$Z_{\mathsf{\rho }}=H_{\mathsf{\rho }}X+V_{\mathsf{\rho }}$$

(16)

where

$$H_{\mathsf{\rho }}=[O_{k\times 6} H_{\mathsf{\rho }1} O_{k\times 6} H_{\mathsf{\rho }2}]$$

(17)

$$H_{\mathsf{\rho }1}=\left[\begin{array}{lll}\frac{\partial {\rho }_1}{\partial x}\hfill & \frac{\partial {\rho }_1}{\partial y}\hfill & \frac{\partial {\rho }_1}{\partial z}\hfill \\ \frac{\partial {\rho }_2}{\partial x}\hfill & \frac{\partial {\rho }_2}{\partial y}\hfill & \frac{\partial {\rho }_2}{\partial z}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ \frac{\partial {\rho }_k}{\partial x}\hfill & \frac{\partial {\rho }_k}{\partial y}\hfill & \frac{\partial {\rho }_k}{\partial z}\hfill \end{array}\right]\Delta C_n^e$$

(18)

$$H_{\mathsf{\rho }2}=\left[\begin{array}{ll}-1\hfill & 0\hfill \\ -1\hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill \\ -1\hfill & 0\hfill \end{array}\right]$$

(19)

where $\Delta C_n^e$ is the coordinate conversion matrix, and its expression is [27]:

$$\Delta C_n^e=\left[\begin{array}{ccc}-(R_n+h)\cos \lambda \sin L& -(R_n+h)\cos L\sin \lambda & \cos L\cos \lambda \\ -(R_n+h)\sin \lambda \sin L& (R_n+h)\cos \lambda \cos L& \cos L\sin \lambda \\ [R_n(1-e^2)+h]\cos L& 0& \sin L\end{array}\right]$$

(20)

The pseudorange rate difference observation equation of INS and GNSS is [26]:

$$\delta {\dot{\rho }}_k=\frac{\partial {\rho }_k}{\partial x}\delta \dot{x}+\frac{\partial {\rho }_k}{\partial y}\delta \dot{y}+\frac{\partial {\rho }_k}{\partial x}\delta \dot{z}-v_{{\dot{\rho }}_k}$$

(21)

We convert the velocity error into the ECEF coordinate system, and we can obtain [28]:

$$\left[\begin{array}{c}\delta \stackrel{\cdot }{x}\\ \delta \stackrel{\cdot }{y}\\ \delta \stackrel{\cdot }{z}\end{array}\right]=C_n^e\left[\begin{array}{c}\delta V_E\\ \delta V_N\\ \delta V_U\end{array}\right]$$

(22)

Comparing Equation (16), we can obtain the pseudorange rate measurement equation as follows:

$$Z_{\dot{\mathsf{\rho }}}=H_{\dot{\mathsf{\rho }}}X+V_{\dot{\mathsf{\rho }}}$$

(23)

where

$$H_{\dot{\mathsf{\rho }}}=[O_{k\times 3}{H}_{\dot{\mathsf{\rho }}1}{O}_{k\times 9}{H}_{\dot{\mathsf{\rho }}2}]$$

(24)

$$H_{\dot{\mathsf{\rho }}1}=\left[\begin{array}{lll}\frac{\partial {\rho }_1}{\partial x}\hfill & \frac{\partial {\rho }_1}{\partial y}\hfill & \frac{\partial {\rho }_1}{\partial z}\hfill \\ \frac{\partial {\rho }_2}{\partial x}\hfill & \frac{\partial {\rho }_2}{\partial y}\hfill & \frac{\partial {\rho }_2}{\partial z}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill \\ \frac{\partial {\rho }_k}{\partial x}\hfill & \frac{\partial {\rho }_k}{\partial y}\hfill & \frac{\partial {\rho }_k}{\partial z}\hfill \end{array}\right]C_n^e$$

(25)

$$H_{\dot{\mathsf{\rho }}2}=\left[\begin{array}{ll}-1\hfill & 0\hfill \\ -1\hfill & 0\hfill \\ ⋮\hfill & ⋮\hfill \\ -1\hfill & 0\hfill \end{array}\right]$$

(26)

where the coordinate conversion matrix $C_n^e$ is [28]:

$$C_n^e=\left[\begin{array}{ccc}-\sin \lambda & -\sin L\cos \lambda & \cos L\cos \lambda \\ \cos \lambda & -\sin L\sin \lambda & \cos L\sin \lambda \\ 0& \cos L& \sin L\end{array}\right]$$

(27)

Finally, the combined observation equation can be obtained:

$$Z(t)=H(t)X(t)+V(t)$$

(28)

that is,

$$\left[\begin{array}{l}{Z}_{\mathsf{\rho }}(t)\\ Z_{\dot{\mathsf{\rho }}}(t)\end{array}\right]=\left[\begin{array}{c}{H}_{\mathsf{\rho }}(t)\\ H_{\dot{\mathsf{\rho }}}(t)\end{array}\right]X(t)+\left[\begin{array}{l}{V}_{\mathsf{\rho }}(t)\\ V_{\dot{\mathsf{\rho }}}(t)\end{array}\right]$$

(29)

3.3. Error and Noise Model

3.3.1. GNSS Environmental Error Model

(1)

Ionospheric and tropospheric error models

Satellite signals will be refracted in the ionosphere and troposphere, which will cause signal delay, and will affect the measurement of pseudorange and pseudorange rate, therefore, we need to correct the pseudorange and pseudorange rate by using the following ionospheric and tropospheric approximate models [29,30,31]:

$${\sigma }_I\sim {\left[1-{(\frac{R_0\cos \varphi }{R_0+h_0})}^2\right]}^{-1/2}$$

(30)

$${\sigma }_T\sim {\left[1-{(\frac{\cos \varphi }{1.001})}^2\right]}^{-1/2}$$

(31)

where ${\sigma }_I$ and ${\sigma }_T$ are the code ionospheric and tropospheric errors, respectively; $R_0$ is the average earth radius, $\varphi$ is the satellite elevation angle, and $h_0$ is the average height of the ionosphere.

(2)

Multipath and NLOS error model

Due to the multipath effect, NLOS causes pseudorange measurement errors and carrier phase measurement errors, which affect the accuracy of satellite navigation and positioning, therefore, according to the reference [32], we model according to the direct signal relative to the multipath signal amplitude (Signal-to-Multipath Ratio, SMR), which is different from the reference [32]. We model the multipath and NLSO together. This can indicate that the multipath and NLOS phenomena occur separately or at the same time, although they are different physical phenomena. This model is simple and practical, avoiding the complexities of multipath and NLOS modeling, ignoring the number of multipath paths and reducing the unnecessary confusion with NLOS. The model was created as follows.

$$SMR=\frac{1}{{\alpha }_{Mult+NLSO}}\stackrel{let}{=}\frac{1}{\alpha }$$

(32)

where $\alpha$ is the amplitude of the multipath or NLOS relative to the direct signal. Here, we have normalized the direct signal. To facilitate analysis, we define the multipath signal relative to the direct signal amplitude (Multipath- to -Signal Ratio, MSR), and according to (32), we get:

$$MSR=\frac{1}{SMR}=\alpha$$

(33)

Usually, we think that when the amplitude of the multipath or NLSO signal is equivalent to the direct signal, i.e., $\alpha$ = 1, we cannot identify whether the received signal is a direct signal or a multipath/NLOS signal [32]. When $\alpha$ = 0, which is an ideal situation, we considered there to be no multipath or NLSO signal at this time, therefore, the value of $\alpha$ was usually between 0 to 1.

3.3.2. Noise Model

In communication and navigation systems, especially when analyzing and calculating the anti-noise performance of the system, we usually assume that the channel noise is Gaussian white noise in the system of navigation, which reflects the noise situation in the actual channel and more truly represents the characteristics of the channel noise. The mathematical model of probability density as follows [33]:

$$p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}$$

(34)

where $\mu$ is the mathematical expectation of noise, and ${\sigma }^2$ is the variance of noise.

In general, we use the signal-to-noise ratio (SNR) to express the strength of the signal, due to the SNR values of different ranging codes [34,35]. However, the LEO constellation is still in the verification and deployment stage, and the relevant technical details on the signal design of navigation enhancement have not been announced. Therefore, we use the signal strength model to describe the SNR, which avoids SNR parameter settings for specific signals, and indicates a unified conversion to signal strength. The signal strength model is currently the most commonly used random model based on SNR. In comparison with other SNR models, the structure of this model is relatively simple and does not require any prior parameters. It can be defined as [36]:

$$SNR=\frac{Signal intensity}{Noise intensity}$$

(35)

3.3.3. Error model of Inertial Navigation System

The main sources of inertial navigation errors are gyroscopes and accelerometers, which have corresponding error models. Due to space limitations, we do not introduce them here, and give the corresponding error models directly. For details, see reference [19].

(1)

Gyro error model

$${\epsilon }_{Gj}(t)={\epsilon }_{cj}(t)+{\epsilon }_{rj}(t)+{\epsilon }_{irj}(t),\hspace{1em}\hspace{1em}(j=x,y,z)$$

(36)

where ${\epsilon }_{cj}(t)$ is the random constant drift, ${\epsilon }_{rj}(t)$ is the correlated drift, and ${\epsilon }_{irj}(t)$ is the uncorrelated drift.

(2)

Accelerometer error model

$${\epsilon }_{aj}={\epsilon }_{bj}+{\sigma }_{wj}\hspace{1em}\hspace{1em}(j=x,y,z)$$

(37)

where ${\epsilon }_{bj}$ is the offset of the accelerometer, and ${\sigma }_{wj}$ is the white noise error.

4. Simulation Analysis

4.1. Parameter Settings

(1)

Parameters of SpaceX LEO Constellation System

Without loss of generality, we use the SpaceX core system constellation for simulation analysis. Its main parameters are shown in

Table 1. The Core Constellation of SpaceX Parameters.

Orbital Parameter Type	Value	Error Parameter Type	Value
Period (min)	About 120	Number of surfaces	32
Height (km) Radius (km) Inclination (°)	1150 7521 53	Number of satellites per orbit Total number of satellites	50 1600

.

(2)

IMU model parameters

IMU model parameters were selected based on low cost. The main parameters are shown in

Table 2. IMU main parameters.

Parameter Type	Accelerometer	Gyro	Cost Level
Quantization noise (m/s2)	1 × 10−4	1 × 10−4	Low
Scale factor (ppm)	100~500	100~500	Low
Cross-coupling error (ppm)	100~500	100~500	Low

.

For the UKF-related parameters, we assume that the initial attitude error, initial position error, and initial velocity error are all zero, and we assume that the initial velocity of the carrier is 200 m/s. In addition, we assume that the positions of the carrier are −3.5958° E, 50.425° N, at an altitude of 10,000 m; the initial pitch, roll, and yaw angles are 0°, 0°, and 90°, respectively; the carrier was set to fly during the process, there were two 45° turns in opposite directions, and a 500 m altitude climb was completed at the same time.

(3)

Environmental interference parameter setting

Other environmental parameter settings are shown in

Table 3. Environmental parameters.

Orbital Parameter Type	Value	Error Parameter Type	Value
Signal spatial error (m)	0.01	Range rate tracking error (m/s)	0.002
Signal ionospheric delay (m)	0.02	Distance noise (m)	0.5
Signal tropospheric delay (m)	0.002	Range rate noise (m/s)	0.05
Code tracking error (m)	0.1	MSR	0.55

.

4.2. Simulation and Result Analysis

4.2.1. Standard INS+LEO2-Satellite Integrated Navigation Algorithm

The research object of the experiment is the aerial vehicle, and the navigation satellite system is the SpaceX satellite system in the LEO constellations. The research scenario is through two satellites + INS in SpaceX combined with the integrated navigation filtering method, completing a three-dimensional position calculation of the carrier. The simulation result from the standard INS+LEO2-satellite integrated navigation and positioning is shown in Figure 3 (in the figure, EPE (East position error, EPE), EVE (East velocity error, EVE) and AEE (Attitude error of east, AEE), respectively represent the position error, velocity error and attitude error in the east direction, while the other parameters can be deduced by analogy).

From Figure 3 we can see that the standard INS+LEO2-satellite integrated navigation positioning can overcome the INS position divergence and velocity errors, and the final navigation trajectory coincides with the flight trajectory of the carrier. Although the velocity and attitude errors fluctuate, the actual navigation and positioning meet basic location requirements.

4.2.2. INS+LEO2-Satellite Alternate Switching Ranging Integrated Navigation Algorithm

The experimental research object and the navigation satellite system are the same as the standard INS+LEO2-satellite integrated navigation positioning algorithm. The research scenario uses INS combined with two satellites in the SpaceX satellite system to achieve integrated navigation and positioning of the aircraft by alternately switching between the two satellites. Specifically, the research scenario is first divided according to the difference in the satellite orbital surface and phase, into two research sub-scenarios. These are (1) INS+LEO2-satellites on the same orbital surface alternately switching ranging, integrated navigation, and positioning, and (2) INS+LEO2-satellites on the adjacent orbital surface, alternately switching ranging, integrated navigation and positioning. Then in each research sub-scenario, considering that the time for the LEO satellite to pass the zenith is very short (about several min to 10 min [37]), carrier users inevitably have to switch between different LEO satellites (generally between beams) to ensure continuous navigation and positioning services. It is worth mentioning that switching also brings many benefits. On the one hand, in a military scenario, a certain extent of anti-interference ability can be guaranteed, and the shorter the switching time, the less likely interference is. On the other hand, switching between beams can avoid bandwidth occupied for a long time, and therefore bandwidth resources can be fully utilized and waste avoided. However, this is a beam resource management and optimization issue, and we will not consider it here.

Both short and long switching times have advantages and disadvantages. Frequent switching will increase the processing pressure and power consumption of the receiver, and will also affect the ICN communication function. A longer switching time can ensure the operation of navigation and positioning functions without affecting ICN communication functions. However, a longer switching time will also cause an increase in the final navigation and positioning error, due to the cumulative error of the INS, affecting the location service. Therefore, in actual projects, trade-offs should be made according to actual needs. As an experimental analysis, we examined the navigation and positioning effects under alternate intervals of 5 s, 10 s, 30 s and 60 s, at the same time, using the standard INS+LEO2-satellite as a reference, and simulate them together.

(1)

Same orbits surface

Based on the fundamental principle that the altitude angle of the satellite cannot be lower than 10°, we selected two satellites on the same orbital surface that are always visible on the trajectory of the carrier. This experiment simulated two satellites, numbered 233 and 245 on the V orbital surface of the SpaceX satellite system, and named satellites #1 and #2 respectively. The final simulation result is shown in Figure 4.

In Figure 4, one satellite provides the true ranging value on the same orbital surface, and the other satellite provides the virtual ranging value. We find that this algorithm can effectively improve the INS error and suppress its divergence through different switching time intervals. It is more effective in improving the position error and velocity error; the attitude error improvement in the north and up direction also received good results. Judging from the final trajectory, the longitude, latitude and altitude errors were very small. To quantitatively analyze the algorithm’s performance on the same orbital surface, we used the mean and standard deviation as evaluation indicators. We calculated statistics from the final navigation trajectory errors, and the results are shown in

Table 4. The trajectory error statistics.

Error Index	Algorithm	Mean	Std
Longitude (°)	INS+LEO2 5 s/Same orbits surface	−1.1203 × 10−5	1.7047 × 10−4
	INS+LEO2 10 s/Same orbits surface	6.2366 × 10−5	2.1058 × 10−4
	INS+LEO2 30 s/Same orbits surface	−6.4679 × 10−5	2.5468 × 10−4
	INS+LEO2 60 s/Same orbits surface	3.9182 × 10−4	6.4647 × 10−4
	INS	−1.5333 × 10−3	1.4192 × 10−3
Latitude (°)	INS+LEO2 5 s/Same orbits surface	1.1128 × 10−5	1.3245 × 10−4
	INS+LEO2 10 s/Same orbits surface	−1.6601 × 10−5	1.6117 × 10−4
	INS+LEO2 30 s/Same orbits surface	−2.1445 × 10−5	1.9511 × 10−4
	INS+LEO2 60 s/Same orbits surface	−2.3428 × 10−4	4.7607 × 10−4
	INS	2.3666 × 10−3	2.2320 × 10−3
Altitude (m)	INS+LEO2 5 s/Same orbits surface	0.1765	3.0525
	INS+LEO2 10 s/Same orbits surface	1.8892	3.4736
	INS+LEO2 30 s/Same orbits surface	1.9771	4.2247
	INS+LEO2 60 s/Same orbits surface	8.8348	10.9232
	INS	78.8923	74.5186

.

The data in Table 4 show that as the switching time increases, the corresponding longitude, latitude and altitude errors increase accordingly. Relative to simple INS navigation, when the switching time is 5 s, 10 s, 30 s and 60 s, the mean performances with respect to longitude error increased by 99.27%, 95.93%, 95.78% and 74.46%, respectively, and the corresponding standard deviations increased 96.04%, 93.20%, 90.09% and 62.49%, respectively. The improvement in longitude error is very significant. The mean latitude performance also improved significantly, increasing by 99.53%, 99.30%, 99.09%, and 90.10% relative to the INS error, respectively, and the corresponding standard deviation increased by 94.07%, 92.78%, 91.26% and 78.67%, respectively. In terms of altitude error, the mean error increased by 99.78%, 97.61%, 97.49% and 88.80%, and the corresponding standard deviation increased by 95.90%, 95.34%, 94.33% and 85.34%, respectively, with altitude performance increasing by more than 85% in terms of mean and standard deviation.

From the data analysis above, it can be concluded that the INS+LEO2-satellite alternate switching integrated navigation algorithm based on the same orbit surface can effectively overcome the INS divergence problem. Specifically, the improvement in the longitude and altitude error is more prominent, and it is obvious from the figure that as the switching time increases, the corresponding performance shows a downward trend. In general, the INS+LEO2-satellite alternate switching ranging integrated navigation algorithm based on the same orbital surface can meet real-time location service requirements in challenging environments well.

(2)

Adjacent orbits surface

Similarly, according to the fundamental principle that the altitude angle of the satellite cannot be less than 10°, we selected two satellites that are always visible on the aircraft’s trajectory, and which are in the adjacent orbital surface and have adjacent phases. In this experiment, the SpaceX satellite system, with 245 orbital surfaces V and 269 orbital surfaces VI, was selected, and assigned the names satellites #1 and #2, respectively, for simulation. The simulation results are shown in Figure 5.

According to the switching algorithm, on the adjacent orbital surface (Figure 5), where one satellite provides the real ranging value and the other satellite provides the virtual ranging value, INS error is effectively improved, and INS divergence suppressed. The intuitive effect is better than that of the same orbital surface in terms of the position and velocity error and final trajectory error. Similarly, to quantitatively analyze the algorithm’s performance on the adjacent orbit surface, we calculate the final navigation trajectory error, and the results are shown in

Table 5. The trajectory error statistics.

Error Index	Algorithm	Mean	Std
Longitude (°)	INS+LEO2 5 s/Adjacent orbits surface	−0.6539 × 10−5	5.6238 × 10−5
	INS+LEO2 10 s/Adjacent orbits surface	−0.8937 × 10−5	7.9074 × 10−5
	INS+LEO2 30 s/Adjacent orbits surface	2.8691 × 10−5	13.7119 × 10−5
	INS+LEO2 60 s/Adjacent orbits surface	5.1428 × 10−5	19.7866 × 10−5
Latitude (°)	INS+LEO2 5 s/Adjacent orbits surface	−0.0539 × 10−4	4.4523 × 10−5
	INS+LEO2 10 s/Adjacent orbits surface	−0.1351 × 10−4	6.0644 × 10−5
	INS+LEO2 30 s/Adjacent orbits surface	−0.8194 × 10−4	10.3322 × 10−5
	INS+LEO2 60 s/Adjacent orbits surface	−1.8018 × 10−4	14.9197 × 10−5
Altitude (m)	INS+LEO2 5 s/Adjacent orbits surface	−0.0543	0.5229
	INS+LEO2 10 s/Adjacent orbits surface	0.4595	1.8593
	INS+LEO2 30 s/Adjacent orbits surface	0.8353	2.7946
	INS+LEO2 60 s/Adjacent orbits surface	0.8935	3.9934

(the INS error statistics are shown in Table 4, which is not listed here).

From Table 5, we can see that as the switching time increases, the longitude, latitude, and altitude errors also generally show an increasing trend. Compared with simple INS navigation, when the switching time is 5 s, 10 s, 30 s, 60 s, the mean values for longitude error increased by 99.57%, 99.42%, 98.13% and 96.65%, respectively, and the corresponding standard deviations increased with 96.04%, 94.43%, 90.34% and 86.06%, respectively. The mean latitude performance increased by 99.77%, 99.43%, 96.54% and 92.39%, respectively, the standard deviations increased by 98.01%, 97.28%, 95.37% and 93.32%, respectively, the standard deviations are more concentrated, and the performance is also improved to some extent. In terms of altitude error, the mean error increased by 99.93%, 99.42%, 98.94% and 98.88%, respectively, and the corresponding standard deviation increased by 99.30%, 97.50%, 96.25% and 94.64%, respectively, while both the mean and standard deviation of the altitude performance also improved by at least 94%.

From this data analysis, it can be concluded that the INS+LEO2-satellite alternate switching ranging integrated navigation algorithm based on adjacent orbital surfaces can also effectively overcome the INS divergence problem. Based on the results presented in Figure 4, we can preliminarily conclude that the algorithm for adjacent orbits is generally better than that of the same orbits, and therefore is more suitable for real-time location service requirements in challenging environments.

4.3. Algorithm Comparison

In this section, we focus on the comparison of the INS+LEO2-satellite alternate switching algorithm between the same orbit and the adjacent orbit. We compare the INS+LEO2-satellite, the INS+MEO2-satellite and the INS+ inclined geo synchronous orbit (IGSO) 2-satellite switching algorithm. We also use the standard INS+LEO2-satellite as a reference and simulate them together. For ease of representation, we abbreviate the algorithm based on the same orbit as SO, and the algorithm based on adjacent orbits as AO.

4.3.1. Comparison of INS+LEO2-Satellite Alternate Switching Ranging Algorithm Navigation and Positioning in the Same Orbit and Adjacent Orbits

We simulate and compare the INS+LEO2 alternate switching ranging algorithm in the same orbit and adjacent orbits, with the simulation results shown in Figure 6.

Figure 6 shows that the position, velocity, attitude and final trajectory performance of the switching algorithm based on adjacent orbits are generally better than the switching algorithm based on the same orbits. To quantitatively analyze the algorithms’ pros and cons under the same orbit and adjacent orbits, we calculated the percentage of improvement of the adjacent orbit’s algorithm relative to the same orbit’s algorithm in terms of mean and standard deviation. The calculation formula is:

$$\mathrm{Im}\mathrm{p}=\frac{\left|Valu{e}_{i\_AO}\right|-\left|Valu{e}_{i\_SO}\right|}{\left|Valu{e}_{i\_SO}\right|}\begin{array}{cc}\times 100\%& (Value=Mean,Std;i=Longitude,Latitude,Altitude)\end{array}$$

(38)

For example, when the switching time is 5 s, $Value=Mean$, and i = Longitude, according to formula (38) we can obtained $\mathrm{Im}\mathrm{p}=\frac{\left|-1.1203\ast {10}^{-5}\right|-\left|-0.6539*{10}^{-5}\right|}{\left|-1.1203*{10}^{-5}\right|}\times 100\%=41.63\%$, other calculation scenarios can be deduced by analogy. The complete calculation results are shown in Figure 7.

Figure 7 shows that in terms of the longitude, latitude and altitude error, the mean improvement of the algorithm based on adjacent orbits is very obvious compared to the same orbits, and the standard deviation is more concentrated than the same orbits. These results show that the switching algorithm based on adjacent orbits is more robust and reliable, and is more suitable for real-time navigation and positioning requirements in challenging environments.

4.3.2. Comparison of Integrated Navigation and Positioning Algorithm with MEO and IGSO Constellation

To compare the navigation and positioning performance of LEO, MEO and IGSO constellations based on ICN technology, and to explore a reference constellation that is more suitable for ICN solutions, it is necessary to compare and analyze these constellations with different orbital altitudes. Without loss of generality, we only compare the 5 s alternate switching algorithms based on the same orbital surface and adjacent orbital surface. The simulation result of the comparison among the INS+LEO2-satellite 5 s, INS+MEO2-satellite 5 s and INS+IGSO2-satellite 5 s alternate switching ranging integrated navigation algorithms is shown in Figure 8.

Figure 8 shows that the INS+LEO2-satellite 5 s alternate switching ranging integrated navigation algorithm based on the same orbit and adjacent orbit surface is significantly better than the INS+MEO2-satellite 5 s and the INS+IGSO2-satellite 5 s alternate switching ranging integrated navigation algorithm based on the same and adjacent orbit surface. Figure 9 shows the statistical results of the positioning errors of the INS+LEO2-satellite 5 s, the INS+MEO2-satellite 5 s and the INS+IGSO2-satellite 5 s switching algorithm.

The statistical results in Figure 9 are easily interpreted, because in terms of orbital height, IGSO > MEO > LEO, therefore the propagation delay is similar. Moreover, taking into account multipath and noise interference on the propagation path, as well as the ionospheric and tropospheric factors, it is not difficult to comprehend that the IGSO constellation navigation error is greater than that of the MEO constellation, which in turn is greater than that of the LEO constellation. This result is in line with expectations, so we can conclude that the LEO constellation is more suitable for our algorithm than the MEO and IGSO constellations.

5. Robustness Analysis

5.1. Analysis of Positioning Error under Different MSR

According to Equation (32), we set MSR to 0.10, 0.55, and 0.95, respectively. The results are shown in Figure 10.

Figure 10 shows that when MSR = 0.15, the error of the algorithm under the same orbit type is significantly smaller than MSR = 0.55 and MSR = 0.95. That is to say, the interference in rural or suburban areas is significantly smaller than in cities or canyons and harsh, challenging environments, which is consistent with what is known. Error statistics for these situations are shown in Figure 11.

Figure 11 shows that even in harsh and challenging environments, we can use the algorithm based on adjacent orbits, and achieve an accuracy of 2.4177 × 10⁻⁴°, 1.7854 × 10⁻⁴° and 4.7087 m in longitude, latitude and altitude respectively, which can also meet the location service needs of most users.

5.2. Analysis of Navigation and Positioning Errors under Different Noise Intensities

The RINEX2.1 format was used to describe the signal strength. According to the official RINEX2.1 format documentation, the signal strength value range of the observation value is 1~9 [38], with better the observation quality at larger values, where 5 is the critical point for a good quality observation value. We assume that the noise intensity corresponding to Gaussian white noise is 1, then according to Equation (35):

$$SN{R}_0=\frac{1}{Noise intensity}$$

(39)

for other noisy environments, there are:

$$SNR=\frac{1}{k\times Noise intensity}=\frac{1}{k}SN{R}_0$$

(40)

where k is the noise intensity coefficient. Here, we take MSR = 0.55 and take k = 1, k = 5, and k = 9 for simulation according to the reference value given in the RINEX2.1 format. The results are shown in Figure 12.

From Figure 12, we find that when noise is added, various algorithms have certain fluctuations, where the smaller the k, the smaller the fluctuation, which is consistent with Formula (40). We calculate the errors in these cases separately, and the results are shown in Figure 13.

Figure 13 shows that even when the SNR is very low, that is, when k = 1, and we adopt the algorithm based on adjacent orbits, the algorithm’s longitude, latitude, and altitude mean and standard deviation performance are −0.1081 × 10⁻⁴°, 0.5142 × 10⁻⁴°, 0.8353 m, and 1.4920 × 10⁻⁴°, 1.9787 × 10⁻⁴°, 3.9934 m, respectively, which can also meet the location service needs of most users.

5.3. Comparisons with Other Algorithms

We compared the final trajectory error to evaluate the traditional dual-satellite navigation positioning algorithm and the existing advanced positioning algorithm. We chose the traditional dual-satellite positioning algorithm that requires the help of an altimeter (e.g., reference [12,16,39]), the traditional dual-satellite positioning algorithm that requires continuous observation (e.g., reference [9,10,40]), and other 3-satellite advanced positioning algorithms (reference [41,42]) for comparison to verify the advantages of our algorithm. Without loss of generality, in our algorithm we only considered two algorithms based on 5 s switching and 60 s switching between adjacent orbits we transformed and unified the relevant data of these algorithms. Where, “/” means that the original article is not covered or provided, the collated statistical data are shown in

Table 6. INS+LEO2-satellite adjacent orbit alternate switching ranging integrated navigation positioning algorithm and other algorithm error calculation statistics.

Error Index	Algorithm	Mean	Std
Longitude (°)	Algorithm [9]	/	/
	Algorithm [10]	/	/
	Algorithm [12]	/	/
	Algorithm [16]	/	/
	Algorithm [17]	/	/
	Algorithm [39]	1.6753 × 10−4	1.3200 × 10−5
	Algorithm [40]	2.4564 × 10−4	1.5700 × 10−2
	Algorithm [41]	8.2270 × 10−3	1.1150 × 10−3
	Algorithm [42]	2.7791 × 10−5	/
	INS+LEO2 5 s/AO	−0.6539 × 10−5	5.6238 × 10−5
	INS+LEO2 60 s/AO	5.1428 × 10−5	19.7866 × 10−5
Latitude (°)	Algorithm [9]	/	/
	Algorithm [10]	/	/
	Algorithm [12]	/	/
	Algorithm [16]	/	/
	Algorithm [17]	/	/
	Algorithm [39]	1.6000 × 10−3	3.5382 × 10−4
	Algorithm [40]	1.7986 × 10−4	1.3400 × 10−2
	Algorithm [41]	1.0253 × 10−1	3.7700 × 10−4
	Algorithm [42]	2.0918 × 10−5	/
	INS+LEO2 5 s/AO	−0.0539 × 10−4	4.4523 × 10−5
	INS+LEO2 60 s/AO	−1.8018 × 10−4	14.9197 × 10−5
Altitude (m)	Algorithm [9]	/	4.0000
	Algorithm [10]	/	7.4762
	Algorithm [12]	/	9.8869
	Algorithm [16]	/	5.0000
	Algorithm [17]	/	4.3991
	Algorithm [39]	34.6000	6.0518
	Algorithm [40]	35.9300	14.1989
	Algorithm [41]	−0.7636	15.1179
	Algorithm [42]	/	/
	INS+LEO2 5 s/AO	−0.0543	0.5229
	INS+LEO2 60 s/AO	0.8935	3.9934

.

From Table 6, the comparison with traditional algorithms and some 3-satellite existing advanced algorithms shows:

Our algorithm is approximately two or three orders of magnitude higher than traditional dual-satellite algorithms in terms of mean longitude performance. The standard deviation is also relatively stable, especially compared to algorithm [40,41], in which the performance is two or three orders of magnitude higher. Both the mean of longitude and latitude performance are higher than the 3-satellite advanced algorithm [41] when we adopt the 5 s switching algorithm. In altitude performance, regardless of mean or standard deviation, the error of our algorithm is the smallest, indicating that our algorithm is more robust.

From the above analysis, we can see that our algorithm has certain advantages in various indicators when compared with the traditional dual satellite positioning algorithm and some existing 3-satellite advanced positioning algorithms. This is due to some of the algorithms requiring the help of an altimeter to complete the positioning or requiring continuous observation to complete the navigation and positioning, while others require the help of many sensors and use three satellites. These types of algorithms inevitably increase the equipment cost, with volume and power consumption of the carrier increasing accordingly, and real-time performance cannot be guaranteed. Our algorithm does not need to rely on the altimeter and also does not need continuous observation. Real-time location services can be completed only by alternate switching, which ensures real-time location requirements in challenging environments, especially real-time performance, which is particularly important in life search and rescue areas.

6. Discussion, Conclusions and Future Work

6.1. Discussion

The simulation and analysis above shows that:

(1)

When the LEO constellation is applied to TCN technology, switching is inevitable, but a certain anti-interference ability can be obtained through switching, and at the same time, it can provide optimization space for bandwidth resources, which can save bandwidth overhead to a certain extent.

(2)

As the switching time increases, the error of the algorithm also increases, therefore, in the design of engineering application, we should set the switching time according to the actual needs. The shorter the switching time, the better the algorithm performance, but frequent switching will increase the processing pressure and power consumption of the integrated system, while with a longer switching time, the algorithm performance is relatively poor, though it can take into account the development of other services, such as communications services.

(3)

The switching algorithm based on adjacent orbits is better than the algorithm based on the same orbit, therefore, in actual of engineering applications, satellites in adjacent orbits should be selected as much as possible to increase the geometric characteristics of the satellites and help improve positioning accuracy.

(4)

Compared with the high-orbit constellations such as MEO and IGSO, the performance of the alternate switching algorithm based on the LEO constellation is higher, and as the LEO satellites are essentially communication satellites which can eliminate the clock difference between the satellite and the user terminal through the FD system, they are therefore more suitable for ICN design.

(5)

Since LEO satellites are closer to the earth, the relative path loss is less and the signal propagation time delay is shorter. Multipath signal interference is therefore relatively weaker, and the signal interference from noise will be relatively reduced. Compared with the traditional MEO constellation and IGSO constellation algorithms, the switching algorithm based on the LEO constellation therefore has better anti-jamming performance and stronger algorithm robustness, and is more suitable for location service solutions in harsh and challenging environments.

(6)

From the experimental results, we also found that the impact of multipath and NLOS on navigation and positioning performance is more serious than noise interference, therefore, in actual engineering, more energy should be expended on the suppression of multipath and NLOS interference.

6.2. Conclusion and Future Work

We studied the standard INS+LEO2 algorithm based on the LEO constellation, and the dual-satellite alternate navigation and positioning algorithm of the same orbit and adjacent orbits. Combining our simulation results and analysis, we can see that the standard INS+LEO2 algorithm has high navigation and positioning accuracy, the final convergence solution tends to 0, and the final trajectory coincides with the carrier’s flight path, with very small errors. Scenarios with the same orbits and with adjacent orbits were compared, and it is concluded that the switching algorithm for adjacent orbital surfaces is better than the same orbital surface. However, they can effectively suppress the INS divergence problem, and at the same time, they are better than the corresponding MEO and IGSO constellation-based algorithms. Compared with traditional algorithms and some 3-satellite existing advanced algorithms, the performance is also greatly improved. In addition, our algorithm can show good robustness in different multipath or NSLO environments and noise environments, and can provide a reference solution for location services in harsh and challenging environments. Therefore, a dual-satellite alternate switching ranging/INS integrated navigation algorithm for the broadband LEO constellation has a low cost, high engineering ease of use, strong real-time and strong anti-interference ability. It can also complete the navigation and positioning service of a three-dimensional position with only two visible satellites without an altimeter and continuous observation.

To improve our algorithm’s adaptability, robustness and navigation and positioning accuracy, future research will aim to provide an algorithm based on business adaptive switching, anti-multipath or anti-NLOS, and carry out actual verification (if there is an open LEO constellation satellite experimental environment). It will also expand the application to extreme and challenging environments such as inside buildings, under metal roofs or underground. In addition, the research will also focus on addressing the problem of larger errors in the same orbit compared to adjacent orbits, especially the cumulative INS error under a longer switching time and the positioning instability caused by frequent switching. Specific we will consider combining LEO and MEO constellations to enhance the stability of the entire navigation system.