3D Point Cloud Reconstruction Using Inversely Mapping and Voting from Single Pass CSAR Images
Abstract
:1. Introduction
2. Methodology
2.1. Robust Principal Component Analysis
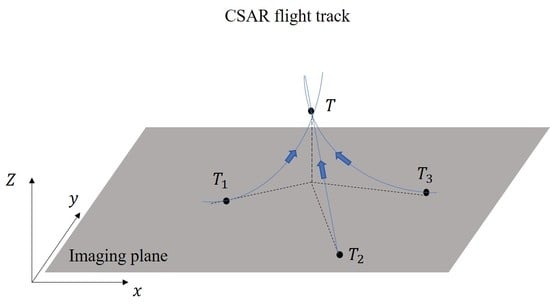
2.2. Inversely Mapping and Voting
3. Experiment and Results
3.1. Results Obtained by the Proposed Method
3.2. Comparison with 3D Imaging Method Using Single Pass of CSAR Data
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, L.; An, D.; Huang, X.; Zhou, Z. A 3D Reconstruction Strategy of Vehicle Outline Based on Single-Pass Single-Polarization CSAR Data. IEEE Trans. Image Process. 2017, 26, 5545–5554. [Google Scholar] [CrossRef] [PubMed]
- Fu, K.; Peng, J.; He, Q.; Zhang, H. Single image 3D object reconstruction based on deep learning: A review. Multimed. Tools Appl. 2020, 80, 463–498. [Google Scholar] [CrossRef]
- Navaneet, K.; Mandikal, P.; Agarwal, M.; Babu, R. CAPNet: Continuous Approximation Projection for 3D Point Cloud Reconstruction Using 2D Supervision. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8819–8826. [Google Scholar] [CrossRef]
- Mandikal, P.; Babu, R. Dense 3D Point Cloud Reconstruction Using a Deep Pyramid Network. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019; pp. 1550–5790. [Google Scholar] [CrossRef] [Green Version]
- Pollefeys, M.; Gool, L.J.V.; Vergauwen, M.; Verbiest, F.; Koch, R. Visual Modeling with a Hand-Held Camera. Int. J. Comput. Vis. 2004, 59, 207–232. [Google Scholar] [CrossRef]
- Streckel, B.; Bartczak, B.; Koch, R.; Kolb, A. Supporting Structure from Motion with a 3D-Range-Camera; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kim, S.J.; Gallup, R.; Frahm, R.M.; Pollefeys, R. Joint radiometric calibration and feature tracking system with an application to stereo. Comput. Vis. Image Underst. 2010, 114, 574–582. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, L.; Cao, Y.; Wu, Z. Attitude Estimation and Geometry Reconstruction of Satellite Targets Based on ISAR Image Sequence Interpretation. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 1698–1711. [Google Scholar] [CrossRef]
- Soumekh, M. Reconnaissance with Slant Plane Circular SAR Imaging. IEEE Trans. Image Process. 1996, 5, 1252–1265. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ponce, O.; Prats-Iraola, P.; Scheiber, R.; Reigber, A.; Moreira, A. First Airborne Demonstration of Holographic SAR Tomography with Fully Polarimetric Multicircular Acquisitions at L-Band. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6170–6196. [Google Scholar] [CrossRef]
- Moore, L.J.; Majumder, U.K. An analytical expression for the three-dimensional response of a point scatterer for circular synthetic aperture radar. In Proceedings of the SPIE-The International Society for Optical Engineering, Beijing, China, 18–19 October 2010; Volume 7699, pp. 223–263. [Google Scholar]
- Ponce, O.; Prats-Iraola, P.; Pinheiro, M.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A.; Moreira, A. Fully Polarimetric High-Resolution 3-D Imaging With Circular SAR at L-Band. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3074–3090. [Google Scholar] [CrossRef]
- Palm, S.; Oriot, H.M. Radargrammetric DEM Extraction Over Urban Area Using Circular SAR Imagery. In Proceedings of the European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010. [Google Scholar]
- Zhang, J.; Suo, Z.; Li, Z.; Zhang, Q. DEM Generation Using Circular SAR Data Based on Low-Rank and Sparse Matrix Decomposition. IEEE Geoence Remote. Sens. Lett. 2018, 15, 724–772. [Google Scholar] [CrossRef]
- Teng, F.; Lin, Y.; Wang, Y.; Shen, W.; Hong, W. An Anisotropic Scattering Analysis Method Based on the Statistical Properties of Multi-Angular SAR Images. Remote Sens. 2020, 12, 2152. [Google Scholar] [CrossRef]
- Ertin, E.; Austin, C.D.; Sharma, S.; Moses, R.L.; Potter, L.C.; Zelnio, E.G.; Garber, F.D. GOTCHA experience report: Three-dimensional SAR imaging with complete circular apertures. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIV, Orlando, FL, USA, 7 May 2007; International Society for Optics and Photonics: Bellingham, WA, USA, 2007; Volume 6568, p. 656802. [Google Scholar]
- Dungan, K.E.; Potter, L.C. 3-D Imaging of Vehicles using Wide Aperture Radar. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 187–200. [Google Scholar] [CrossRef]
- Austin, C.D.; Moses, R.L. Interferometric Synthetic Aperture Radar Detection and Estimation Based 3D Image Reconstruction. In Proceedings of the Conference on Algorithms for Synthetic Aperture Radar Imagery XIII 20060417-20, Kissimmee, FL, USA, 17 May 2006. [Google Scholar]
- Panagiotakis, C. Point clustering via voting maximization. J. Classif. 2015, 32, 212–240. [Google Scholar] [CrossRef]
- Yu, D.; Ji, S.; Liu, J.; Wei, S. Automatic 3D building reconstruction from multi-view aerial images with deep learning. ISPRS J. Photogramm. Remote Sens. 2021, 171, 155–170. [Google Scholar] [CrossRef]
- Salehi, H.; Vahidi, J.; Abdeljawad, T.; Khan, A.; Rad, S.Y.B. A SAR Image Despeckling Method Based on an Extended Adaptive Wiener Filter and Extended Guided Filter. Remote Sens. 2020, 12, 2371. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, H.; Lv, Z. Vehicle Layover Removal in Circular SAR Images via ROSL. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1–5. [Google Scholar] [CrossRef]
- Wen, F.; Ying, R.; Liu, P.; Qiu, R.C. Robust PCA Using Generalized Nonconvex Regularization. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 1497–1510. [Google Scholar] [CrossRef]
- Bouwmans, T.; Javed, S.; Zhang, H.; Lin, Z.; Otazo, R. On the Applications of Robust PCA in Image and Video Processing. Proc. IEEE 2018, 106, 1427–1457. [Google Scholar] [CrossRef] [Green Version]
- Swingle, W.W. Copyright-Constrained Optimization and Lagrange Multiplier Methods. J. Gen. Physiol. 1919, 2, 161–171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gorham, L.A.; Moore, L.J. SAR image formation toolbox for MATLAB. Proc. SPIE 2010, 7699, 223–263. [Google Scholar]
- Feng, S.; Lin, Y.; Wang, Y.; Yang, Y.; Hong, W. DEM Generation With a Scale Factor Using Multi-Aspect SAR Imagery Applying Radargrammetry. Remote Sens. 2020, 12, 556. [Google Scholar] [CrossRef] [Green Version]
- Leberl, F.W. Radargrammetric Image Processing; Technical Report; Artech House: London, UK, 1990. [Google Scholar]
- Casteel, C.H., Jr.; Gorham, L.R.A.; Minardi, M.J.; Scarborough, S.M.; Naidu, K.D.; Majumder, U.K. A challenge problem for 2D/3D imaging of targets from a volumetric data set in an urban environment. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIV, Orlando, FL, USA, 7 May 2007; International Society for Optics and Photonics: Bellingham, WA, USA, 2007. [Google Scholar]
- Voccola, K.; Yazıcı, B.; Ferrara, M.; Cheney, M. On the relationship between the generalized likelihood ratio test and backprojection for synthetic aperture radar imaging. In Proceedings of the Automatic Target Recognition XIX, Orlando, FL, USA, 22 May 2009; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; Volume 7335. [Google Scholar]











| Dimensions | Length (m) | Width (m) | Height (m) |
|---|---|---|---|
| actual value | 4.98 | 1.86 | 1.42 |
| restored value | 4.88 | 1.74 | 1.44 |
| error | 0.10 | 0.12 | −0.02 |
| Dimensions | Length (m) | Width (m) | Height (m) |
|---|---|---|---|
| actual value | 4.75 | 1.74 | 1.41 |
| restored value | 4.60 | 1.60 | 1.40 |
| error | 0.15 | 0.14 | 0.01 |
| Dimensions | Length (m) | Width (m) | Height (m) |
|---|---|---|---|
| actual value | 4.45 | 1.77 | 1.44 |
| restored value | 4.40 | 1.80 | 1.60 |
| error | 0.05 | −0.03 | −0.16 |
| Time-Consuming | 3D Imaging (s) | The Proposed Method (s) |
|---|---|---|
| vehicle C | 8111 | 1023 |
| vehicle B | 7608 | 970 |
| vehicle F | 8135 | 1037 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Lin, Y.; Wang, Y.; Teng, F.; Hong, W. 3D Point Cloud Reconstruction Using Inversely Mapping and Voting from Single Pass CSAR Images. Remote Sens. 2021, 13, 3534. https://doi.org/10.3390/rs13173534
Feng S, Lin Y, Wang Y, Teng F, Hong W. 3D Point Cloud Reconstruction Using Inversely Mapping and Voting from Single Pass CSAR Images. Remote Sensing. 2021; 13(17):3534. https://doi.org/10.3390/rs13173534
Chicago/Turabian StyleFeng, Shanshan, Yun Lin, Yanping Wang, Fei Teng, and Wen Hong. 2021. "3D Point Cloud Reconstruction Using Inversely Mapping and Voting from Single Pass CSAR Images" Remote Sensing 13, no. 17: 3534. https://doi.org/10.3390/rs13173534
APA StyleFeng, S., Lin, Y., Wang, Y., Teng, F., & Hong, W. (2021). 3D Point Cloud Reconstruction Using Inversely Mapping and Voting from Single Pass CSAR Images. Remote Sensing, 13(17), 3534. https://doi.org/10.3390/rs13173534