A Framework for Generating High Spatiotemporal Resolution Land Surface Temperature in Heterogeneous Areas
Abstract
:1. Introduction
2. Study Area and Data Collection
2.1. Study Area
2.2. Data Collection and Image Processing
- (1)
- MODIS product
- (2)
- Landsat 8 product
- (3)
- DEM image
- (4)
- Image processing
3. Methodology
3.1. Overview
3.2. Construction of the Framework
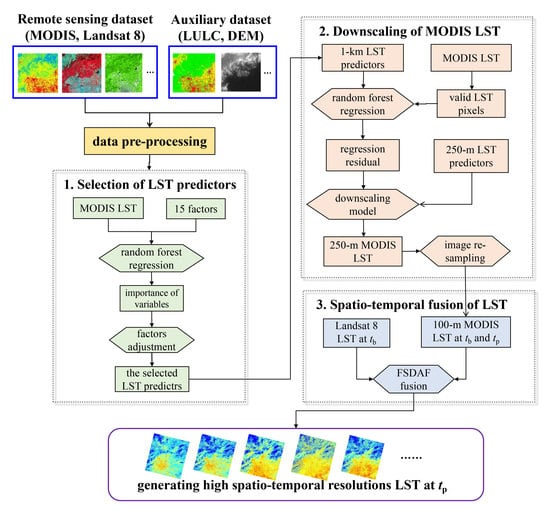
- Step 1: Selection of LST predictors
- Step 2: Downscaling of MODIS LST
- (1)
- The 250-m resolution MOD09GQ product and 30-m resolution GDEM were used to calculate the selected LST predictors and then were aggregated to 1 km and 250 m, respectively. LST predictors with a resolution of 1 km belong to the MOD11A1 pixel level, and LST predictors with a resolution of 250 m belong to the MOD09GQ pixel level.
- (2)
- The RF regression model was used to construct the relationship between MODIS LST and five predictors at the resolution of 1 km, which can be expressed as follows:where LST1km denotes the MODIS LST and is fitted by the RF regression with f as a non-linear function; f denotes the function between LST and its predictors; PV1km is the aggregated PV image using the MOD09GQ with the resolution of 1 km; elevation1km, slope1km, longitude1km and latitude1km are all the aggregated LST predictors derived from the GDEM with the resolution of 1 km; and ε1km is the residual of RF regression at a spatial resolution of 1 km.
- (3)
- By assuming that regression residuals are uniformly distributed in space, the ordinary kriging interpolation were used to interpolate the residual with a 1-km resolution to 250 m.
- (4)
- By assuming that the relationship between LST and its predictors within 1-km resolution is scale-invariant for 250-m resolution, the MODIS LST was sharpened at tb and tp to 250 m based on the linking model at 1-km resolution and combined with the residual and predictors at 250-m resolution:where LST250m is the downscaled MODIS LST with a resolution of 250 m; PV250m is the aggregated PV from the MOD09GQ with a resolution of 250 m; elevation250m, slope250m, longitude250m, and latitude250m are all the aggregated terrain factors derived from the GDEM with a resolution of 250 m; ɛ250m is the regression residual with a resolution of 250 m.
- Step 3: Spatiotemporal image fusion of LST.
3.3. Comparison with Other Methods
3.4. Accuracy Assessment
4. Results
4.1. Selection Analysis of LST Predictors
4.2. Accuracy Evaluation of the Framework
4.3. Distribution Error Analysis of Predicted LSTs
5. Discussion
5.1. Impacts of MODIS LST Downscaling
5.2. Advantages and Disadvantages of the Proposed Framework
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Wang, C.G.; Zhang, S.T.; Tang, B.H.; Leng, P.; Gao, M.F. Land-surface temperature retrieval from Landsat 8 single-channel thermal infrared data in combination with NCEP reanalysis data and ASTER GED product. Int. J. Remote Sens. 2018, 40, 1763–1778. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Mattar, C.; Cristobal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Zhu, X.M.; Song, X.N.; Leng, P.; Guo, D.; Cai, S.H. Impact of atmospheric correction on spatial heterogeneity relations between land surface temperature and biophysical compositions. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2680–2697. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.Z.; Yan, G.J.; Wan, Z.M.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef] [Green Version]
- Duan, S.B.; Li, Z.L. Spatial downscaling of MODIS land surface temperatures using geographically weighted regression case study in Northern China. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Quan, J.L.; Zhan, W.F.; Ma, T.D.; Du, Y.Y.; Guo, Z.; Qin, B.Y. An integrated model for generating hourly Landsat-like land surface temperatures over heterogeneous landscapes. Remote Sens. Environ. 2018, 206, 403–423. [Google Scholar] [CrossRef]
- Stathopoulou, M.; Cartalis, C. Downscaling AVHRR land surface temperatures for improved surface urban heat island intensity estimation. Remote Sens. Environ. 2009, 113, 2592–2605. [Google Scholar] [CrossRef]
- Castelli, M.; Anderson, M.C.; Yang, Y.; Wohlfahrt, G.; Bertoldi, G.; Niedrist, G. Two-source energy balance modeling of evapotranspiration in alpine grasslands. Remote Sens. Environ. 2018, 209, 327–342. [Google Scholar] [CrossRef]
- Lu, D.; Song, K.; Zang, S.; Jia, M.; Jia, D.; Ren, C. The effect of urban expansion on urban surface temperature in Shenyang, China: An analysis with Landsat imagery. Environ. Model. Assess. 2015, 20, 197–210. [Google Scholar] [CrossRef]
- Yu, Y.R.; Duan, S.B.; Li, Z.L.; Chang, S.; Xing, Z.F.; Leng, P.; Gao, M.F. Interannual spatiotemporal variations of land surface temperature in China from 2003 to 2018. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 1783–1795. [Google Scholar] [CrossRef]
- Zhao, W.; He, J.; Wu, Y.; Xiong, D.; Wen, F.; Li, A. An analysis of land surface temperature trends in the central Himalayan region based on MODIS products. Remote Sens. 2019, 11, 900. [Google Scholar] [CrossRef] [Green Version]
- Xia, H.P.; Chen, Y.H.; Li, Y.; Quan, J.L. Combining kernel-driven and fusion-based methods to generate daily high-spatial-resolution land surface temperatures. Remote Sens. Environ. 2019, 224, 259–274. [Google Scholar] [CrossRef]
- Yoo, C.; Im, J.; Park, S.; Cho, D. Spatial downscaling of MODIS land surface temperature: Recent research trends, challenges, and future directions. Korean J. Remote Sens. 2020, 36, 609–626. [Google Scholar]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Dominguez, A.; Kleissl, J.; Luvall, J.C.; Rickman, D.L. High-resolution urban thermal sharpener (HUTS). Remote Sens. Environ. 2011, 115, 1772–1780. [Google Scholar] [CrossRef] [Green Version]
- Bindhu, V.M.; Narasimhan, B.; Sudheer, K.P. Development and verification of a non-linear disaggregation method (NL-DisTrad) to downscale MODIS land surface temperature to the spatial scale of Landsat thermal data to estimate evapotranspiration. Remote Sens. Environ. 2013, 135, 118–129. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Weng, Q.H.; Fu, P.; Gao, F. Generating daily land surface temperature at landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Wu, M.; Li, H.; Huang, W.; Niu, Z.; Wang, C. Generating daily high spatial land surface temperatures by combining ASTER and MODIS land surface temperature products for environmental process monitoring. Environ. SCI-Proc. IMP 2015, 17, 1396–1404. [Google Scholar] [CrossRef]
- Wu, P.H.; Shen, H.F.; Zhang, L.P.; Göttsche, F.M. Integrated fusion of multi-scale polar-orbiting and geostationary satellite observations for the mapping of high spatial and temporal resolution land surface temperature. Remote Sens. Environ. 2015, 156, 169–181. [Google Scholar] [CrossRef]
- Yang, G.J.; Weng, Q.H.; Pu, R.L.; Gao, F.; Sun, C.H.; Li, H.; Zhao, C.J. Evaluation of ASTER-like daily land surface temperature by fusing ASTER and MODIS data during the HiWATER-MUSOEXE. Remote Sens. 2016, 8, 75. [Google Scholar] [CrossRef] [Green Version]
- Xia, H.P.; Chen, Y.H.; Zhao, Y.T.; Chen, Z.Y. “Regression-then-Fusion” or “Fusion-then-Regression”? A theoretical analysis for generating high spatiotemporal resolution land surface temperatures. Remote Sens. 2018, 10, 1382. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Moosavi, V.; Talebi, A.; Mokhtari, M.H.; Shamsi, S.; Niazi, Y. A wavelet-artificial intelligence fusion approach (WAIFA) for blending Landsat and MODIS surface temperature. Remote Sens. Environ. 2015, 169, 243–254. [Google Scholar] [CrossRef]
- Yang, G.J.; Pu, R.L.; Zhao, C.J.; Huang, W.J.; Wang, J.H. Estimation of subpixel land surface temperature using an endmember index based technique: A case examination on ASTER and MODIS temperature products over a heterogeneous area. Remote Sens. Environ. 2011, 115, 1202–1219. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, S.M.; Li, M.S.; Zhan, W.F.; Xu, Z.W.; Xu, T.R. Quantification of the scale effect in downscaling remotely sensed land surface temperature. Remote Sens. 2016, 8, 975. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Wong, M.S.; Shi, W.Z.; Wu, L.X.; Qin, K. Advancing of land surface temperature retrieval using extreme learning machine and spatio-temporal adaptive data fusion algorithm. Remote Sens. 2015, 7, 4424–4441. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Wan, Z.M. New refinements and validation of the collection-6 MODIS land-surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Li, H.; Göttsche, F.M.; Wu, H.; Zhao, W.; Leng, P.; Zhang, X.; Coll, C. Validation of Collection 6 MODIS land surface temperature product using in situ measurements. Remote Sens. Environ. 2019, 225, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.M.; Zhang, Z.J.; Hu, T.; Wang, G.Z.; He, G.J.; Zhang, Z.M.; Li, H.; Wu, Z.J.; Liu, X. An efficient framework for producing Landsat based land surface temperature data using google earth engine. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 4689–4701. [Google Scholar] [CrossRef]
- Zhang, Z.M.; He, G.J.; Wang, M.M.; Long, T.F.; Wang, G.Z.; Zhang, X.M.; Jiao, W.L. Towards an operational method for land surface temperature retrieval from Landsat 8 data. Remote Sens. Lett. 2016, 7, 279–288. [Google Scholar] [CrossRef]
- Peng, X.; Wu, W.; Zheng, Y.; Sun, J.; Hu, T.; Wang, P. Correlation analysis of land surface temperature and topographic elements in Hangzhou, China. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Chaieb, A.; Rebair, N.; Bouazizb, S. Vertical accuracy assessment of SRTM Ver 4.1 and ASTER GDEM Ver 2 using GPS measurements in central west of Tunisia. J. GIS 2016, 8, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef] [Green Version]
- Bonafoni, S. Downscaling of Landsat and MODIS land surface temperature over the heterogeneous urban area of Milan. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 2019–2027. [Google Scholar] [CrossRef]
- Tang, K.; Zhu, H.C.; Ni, P. Spatial downscaling of land surface temperature over heterogeneous regions using random forest regression considering spatial features. Remote Sens. 2021, 13, 3645. [Google Scholar] [CrossRef]
- Wang, S.M.; Luo, X.B.; Peng, Y.D. Spatial downscaling of MODIS land surface temperature based on geographically weighted autoregressive model. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 2532–2546. [Google Scholar] [CrossRef]
- Yang, Y.B.; Cao, C.; Pan, X.; Li, X.L.; Zhu, X. Downscaling land surface temperature in an arid area by using multiple remote sensing indices with Random Forest regression. Remote Sens. 2017, 9, 789. [Google Scholar] [CrossRef] [Green Version]
- Zhan, W.F.; Chen, Y.H.; Wang, J.F.; Zhou, J.; Quan, J.L.; Liu, W.Y.; Li, J. Downscaling land surface temperatures with multi-spectral and multi-resolution images. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 23–36. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jimenez-Muoz, J.C.; Soria, G.; Romaguera, M.; Guanter, L.; Moreno, J. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Zhu, X.M.; Wang, X.H.; Yan, D.J.; Liu, Z.; Zhou, Y.F. Analysis of remotely-sensed ecological indexes’ influence on urban thermal environment dynamic using an integrated ecological index: A case study of Xi’an, China. Int. J. Remote Sens. 2019, 40, 3421–3447. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach Learn 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.L.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Duan, S.B.; Li, A.N.; Yin, G.F. A practical method for reducing terrain effect on land surface temperature using random forest regression. Remote Sens. Environ. 2019, 221, 635–649. [Google Scholar] [CrossRef]
- Bisquert, M.; Juan, M.S.; Caselles, V. Evaluation of disaggregation methods for downscaling MODIS land surface temperature to Landsat spatial resolution in Barrax test site. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 1430–1438. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L.; Leng, P. A framework for the retrieval of all-weather land surface temperature at a high spatial resolution from polar-orbiting thermal infrared and passive microwave data. Remote Sens. Environ. 2017, 195, 107–117. [Google Scholar] [CrossRef]
- Long, D.; Yan, L.; Bai, L.L.; Zhang, C.; Shi, C. Generation of MODIS-like land surface temperatures under all-weather conditions based on a data fusion approach. Remote Sens. Environ. 2020, 246, 111863. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S.B. Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 2020, 247, 111931. [Google Scholar] [CrossRef]











| Satellite | Data Collection | Factors Provided | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| Terra/MODIS | MOD11A1 | LST, LSE | 1-km | 1 day |
| MOD09GQ | NDVI, PV | 250-m | 1 day | |
| MOD09GA | NDVI, PV, SAVI, NDMI, NDBI, BSI, IEI, MNDWI | 500-m | 1 day | |
| MCD12Q1 | LULC | 500-m | 1 year | |
| Landsat 8 | RTU LST product | LST | 100-m | 16 days |
| ASTER | ASTER GDEM | longitude, latitude, elevation, slope, aspect | 30-m |
| Factors | %IncMSE | IncNode Purity | IC | Factors | %IncMSE | IncNode Purity | IC |
|---|---|---|---|---|---|---|---|
| PV | 14.855 | 29,980.19 | 14,997.52 | NDBI | 12.62 | 1942.49 | 977.55 |
| NDVI | 12.48 | 23,415.53 | 11,714.01 | Slope (°) | 23.13 | 1735.58 | 879.36 |
| Elevation (m) | 47.51 | 10,778.17 | 5412.84 | LSE | 18.47 | 1225.81 | 622.14 |
| NDMI | 10.21 | 8176.55 | 4093.38 | IEI | 6.01 | 1183.08 | 594.55 |
| BSI | 5.42 | 7164.63 | 3585.02 | MNDWI | 15.33 | 854.29 | 434.81 |
| SAVI | 5.82 | 4341.67 | 2173.75 | aspect | 1.58 | 561.02 | 281.30 |
| Longitude (°) | 44.10 | 3932.90 | 1988.50 | LULC | 2.04 | 45.36 | 23.70 |
| Latitude (°) | 38.30 | 3148.78 | 1593.54 |
| Image ID | Error Levels (K) | Three-Step Method | RF Strategy | STARFM-Based Fusion | RF-Based Downscaling |
|---|---|---|---|---|---|
| A1 | 0–1 | 43.96 | 39.06 | 26.86 | 7.04 |
| 1–2 | 35.12 | 30.66 | 25.79 | 7.78 | |
| 2–3 | 14.24 | 16.80 | 17.26 | 9.05 | |
| 3–5 | 4.50 | 9.50 | 15.05 | 21.24 | |
| >5 | 2.18 | 3.93 | 15.02 | 54.89 | |
| B1 | 0–1 | 42.30 | 43.26 | 30.05 | 21.83 |
| 1–2 | 31.65 | 30.92 | 25.50 | 25.88 | |
| 2–3 | 16.50 | 15.76 | 18.54 | 24.18 | |
| 3–5 | 9.25 | 9.59 | 18.16 | 23.11 | |
| >5 | 0.30 | 0.47 | 7.75 | 5.00 |
| LULC Types | Three-Step Method | RF Strategy | STARFM-Based Fusion | RF-Based Downscaling | Mean Error |
|---|---|---|---|---|---|
| Cultivated land | 1.36 | 1.63 | 2.48 | 4.36 | 2.45 |
| Grassland | 1.59 | 2.02 | 3.91 | 9.14 | 4.16 |
| Shrub land | 1.62 | 1.67 | 2.07 | 3.40 | 2.19 |
| Artificial surface | 1.33 | 1.44 | 2.30 | 4.13 | 2.30 |
| Bare land | 3.30 | 6.07 | 5.78 | 10.3 | 6.36 |
| Mean error | 1.84 | 2.56 | 3.31 | 6.27 |
| LULC Types | Three-Step Method | RF Strategy | STARFM-Based Fusion | RF-Based Downscaling | Mean Error |
|---|---|---|---|---|---|
| Cultivated land | 1.24 | 1.24 | 1.78 | 1.58 | 1.46 |
| Grassland | 1.00 | 0.98 | 1.83 | 2.03 | 1.46 |
| Shrub land | 1.07 | 1.08 | 1.81 | 2.66 | 1.65 |
| Artificial surface | 2.29 | 2.34 | 3.07 | 3.11 | 2.70 |
| Bare land | 1.38 | 1.62 | 1.64 | 2.77 | 2.43 |
| Mean error | 1.39 | 1.45 | 2.03 | 2.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Song, X.; Leng, P.; Li, X.; Gao, L.; Guo, D.; Cai, S. A Framework for Generating High Spatiotemporal Resolution Land Surface Temperature in Heterogeneous Areas. Remote Sens. 2021, 13, 3885. https://doi.org/10.3390/rs13193885
Zhu X, Song X, Leng P, Li X, Gao L, Guo D, Cai S. A Framework for Generating High Spatiotemporal Resolution Land Surface Temperature in Heterogeneous Areas. Remote Sensing. 2021; 13(19):3885. https://doi.org/10.3390/rs13193885
Chicago/Turabian StyleZhu, Xinming, Xiaoning Song, Pei Leng, Xiaotao Li, Liang Gao, Da Guo, and Shuohao Cai. 2021. "A Framework for Generating High Spatiotemporal Resolution Land Surface Temperature in Heterogeneous Areas" Remote Sensing 13, no. 19: 3885. https://doi.org/10.3390/rs13193885
APA StyleZhu, X., Song, X., Leng, P., Li, X., Gao, L., Guo, D., & Cai, S. (2021). A Framework for Generating High Spatiotemporal Resolution Land Surface Temperature in Heterogeneous Areas. Remote Sensing, 13(19), 3885. https://doi.org/10.3390/rs13193885