Automatic Landform Recognition from the Perspective of Watershed Spatial Structure Based on Digital Elevation Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Quantification of the Watershed Spatial Structure and Its Composition
- (1)
- Gully densities under each flow accumulation threshold (100, 200, 300, …, 1000) were calculated to be a sequence [, ], where is the number of . Then, we calculated the mean value of the sequence as and the deviation square sum for the sequence as .
- (2)
- The sequence of can be divided into two sequences [{,}, {,}, … {,}]. is obtained by adding the sum of deviation square between the two preceding samples and can be calculated using the following:
2.2.1. The Stable Watershed Area Based on the Slope Spectrum
- (1)
- Calculate the slope map of the catchment area using the mesh-based clustering algorithm proposed by Zevenbergen [95].
- (2)
- (3)
- The stability of the slope spectrum for the extracted watershed can be measured by the extracted slope spectrum with the referred slope spectrum. Defining the slope spectrum of the watershed before expanding as , where is the percentage of the area within the slope class in the catchment area. Similarly, defining the slope spectrum of the watershed after expanding as . Then, we defined the quantitative indices of similarity as and , which take the forms and .
- (4)
- The watershed area continuously expanded by adding the new watershed unit to the catchment area. When there were 30 continuous cases where and , we viewed as the stable slope spectrum and the watershed area of the first case as the stable watershed area (see Figure 5).
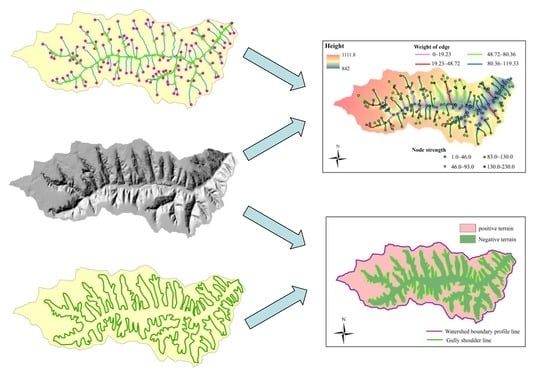
2.2.2. Extracting the P–N Spatial Structure of the Watershed
2.2.3. Extracting the WWCN Spatial Structure of the Watershed
2.2.4. The Quantitative Description of the WWCN Spatial Structure and P–N Terrain Spatial Structure
2.3. Light Gradient Boosting Machine
2.4. Evaluation Criterion and Experimental Design
3. Results and Discussions
3.1. The Stable Area of the Watershed
3.2. Recognition Result Based on Different Watershed Spatial Structures
3.3. Importances of Different Comprehensive Quantitative Indexes
3.4. Comparison with the Fusion of Terrain Derivatives and Texture Derivatives
3.5. Comparison with Other Popular Machine Learning Methods
3.6. Innovations of This Study
3.7. Possible Limitations
4. Conclusions
- (1)
- The watershed structure-based method is an effective landform recognition theory with rich potential in the landform recognition field of using the watershed as a basic unit. The fusion of the WWCN spatial structure and the P–N terrain structure can significantly improve the landform recognition performance. It is noted that the WWCN is the first attempt of the complex network theory in the landform recognition field.
- (2)
- Without using a uniform area as a criterion for watershed area division, the slope spectrum method is used to determine the stable area of the watershed. It provides additional insights for the area determination of the watershed.
- (3)
- The landform recognition performance and robustness based on the combination of the WWCN and P–N terrain outperformed that based on the terrain derivatives and texture derivatives, thereby suggesting the great significance of our study.
- (4)
- The methods from the angle of the watershed spatial structure and composition seemed to be well adapted to some similar or complex landforms. The loess ridge and loess hill are generally difficult to distinguish via landform recognition or artificial discrimination. The proposed method is effective in alleviating the confusion of the two kinds of similar landforms. By adopting the combination of the WWCN and P–N terrain to simulate the watershed spatial structure, the F1 values reached 95.4% and 100%, respectively, which was better than the method based on the basic terrain indices.
- (5)
- The LightGBM algorithm is suitable to be employed for the landform recognition of the watershed structure-based method since it showed better performance than the other machine learning methods.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mokarram, M.; Sathyamoorthy, D. A review of landform classification methods. Spat. Inf. Res. 2018, 26, 647–660. [Google Scholar] [CrossRef]
- Moreno, M.; Levachkine, S.; Torres, M.; Quintero, R. Landform classification in raster geo-images. In Progress in Pattern Recognition, Image Analysis and Applications; Sanfeliu, A., Trinidad, J.F.M., Ochoa, J.A.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2004; Volume 3287, pp. 558–565. [Google Scholar]
- Wang, Y.; Qin, C. Review of automatic classification methods for geomorphic morphological types. Geogr. Geo Inf. Sci. 2017, 33, 16–21. [Google Scholar]
- Kilic Gul, F. Geomorphometry-Automatic Landform Classification. J. Geogr. Cograf. Derg. 2018, 36, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Laffan, S.W.; Liu, Y.; Wu, L. Morphometric characterisation of landform from DEMs. Int. J. Geogr. Inf. Sci. 2010, 24, 305–326. [Google Scholar] [CrossRef] [Green Version]
- Evans, I.S. Geomorphometry and landform mapping: What is a landform? Geomorphology 2012, 137, 94–106. [Google Scholar] [CrossRef]
- Jasiewicz, J.; Stepinski, T.F. Geomorphons—A pattern recognition approach to classification and mapping of landforms. Geomorphology 2013, 182, 147–156. [Google Scholar] [CrossRef]
- Hiller, J.; Smith, M. Residual relief separation: Digital elevation model enhancement for geomorphological mapping. Earth Surf. Process. Landf. 2008, 33, 2266–2276. [Google Scholar] [CrossRef] [Green Version]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Du, L.; You, X.; Li, K.; Meng, L.; Cheng, G.; Xiong, L.; Wang, G. Multi-modal deep learning for landform recognition. ISPRS J. Photogramm. Remote Sens. 2019, 158, 63–75. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, G.; Yang, X.; Li, F. Geomorphology-oriented digital terrain analysis: Progress and perspectives. J. Geogr. Sci. 2021, 31, 456–476. [Google Scholar] [CrossRef]
- Burrough, P.A.; van Gaans, P.F.; MacMillan, R. High-resolution landform classification using fuzzy k-means. Fuzzy Sets Syst. 2000, 113, 37–52. [Google Scholar] [CrossRef]
- Zhao, W.-F.; Xiong, L.-Y.; Ding, H.; Tang, G.-A. Automatic recognition of loess landforms using Random Forest method. J. Mt. Sci. 2017, 14, 885–897. [Google Scholar] [CrossRef]
- Tribe, A. Automated recognition of valley heads from digital elevation models. Earth Surf. Process. Landf. 1991, 16, 33–49. [Google Scholar] [CrossRef]
- Bishop, M.P.; James, L.A.; Shroder, J.F., Jr.; Walsh, S.J. Geospatial technologies and digital geomorphological mapping: Concepts, issues and research. J. Geomorphol. 2012, 137, 5–26. [Google Scholar] [CrossRef]
- Hammond, E.H. Analysis of properties in land form geography: An application to broad-scale land form mapping. Ann. Assoc. Am. Geogr. 1964, 54, 11–19. [Google Scholar] [CrossRef]
- MacMillan, R.A.; Pettapiece, W.W.; Nolan, S.C.; Goddard, T.W. A generic procedure for automatically segmenting landforms into landform elements using DEMs, heuristic rules and fuzzy logic. Fuzzy Sets Syst. 2000, 113, 81–109. [Google Scholar] [CrossRef]
- Saha, K.; Wells, N.A.; Munro-Stasiuk, M. An object-oriented approach to automated landform mapping: A case study of drumlins. Comput. Geosci. 2011, 37, 1324–1336. [Google Scholar] [CrossRef]
- Smith, M.J. Digital Mapping: Visualisation, interpretation and quantification of landforms. In Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2011; Volume 15, pp. 225–251. [Google Scholar]
- Stepinski, T.F.; Ghosh, S.; Vilalta, R. Automatic recognition of landforms on Mars using terrain segmentation and classification. In Proceedings of the International Conference on Discovery Science, Barcelona, Spain, 7–10 October 2006; pp. 255–266. [Google Scholar]
- Migoń, P.; Woo, K.-S.; KaSprzaK, M. Landform recognition in granite mountains in East Asia (Seoraksan, Republic of Korea, and Huangshan and Sanqingshan, China)—A contribution of geomorphology to the UNESCO World Heritage. Quaest. Geogr. 2018, 37, 103–115. [Google Scholar] [CrossRef] [Green Version]
- Kasprzak, M.; Jancewicz, K.; Różycka, M.; Kotwicka, W.; Migoń, P. Geomorphology-and geophysics-based recognition of stages of deep-seated slope deformation (Sudetes, SW Poland). Eng. Geol. 2019, 260, 105230. [Google Scholar] [CrossRef]
- Yang, X.; Tang, G.; Meng, X.; Xiong, L. Classification of Karst Fenglin and Fengcong Landform Units Based on Spatial Relations of Terrain Feature Points from DEMs. Remote Sens. 2019, 11, 1950. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Xiong, L.; Tang, G.; Strobl, J. Deep learning-based approach for landform classification from integrated data sources of digital elevation model and imagery. Geomorphology 2020, 354, 107045. [Google Scholar] [CrossRef]
- Zhou, X.; Xie, X.; Xue, Y.; Xue, B.; Qin, K.; Dai, W. Bag of Geomorphological Words: A Framework for Integrating Terrain Features and Semantics to Support Landform Object Recognition from High-Resolution Digital Elevation Models. ISPRS Int. J. Geo-Inf. 2020, 9, 620. [Google Scholar] [CrossRef]
- Janušaitė, R.; Jukna, L.; Jarmalavičius, D.; Pupienis, D.; Žilinskas, G. A Novel GIS-Based Approach for Automated Detection of Nearshore Sandbar Morphological Characteristics in Optical Satellite Imagery. Remote Sens. 2021, 13, 2233. [Google Scholar] [CrossRef]
- Xiong, L.-Y.; Zhu, A.-X.; Zhang, L.; Tang, G.-A. Drainage basin object-based method for regional-scale landform classification: A case study of loess area in China. Phys. Geogr. 2018, 39, 523–541. [Google Scholar] [CrossRef]
- Cao, Z.; Fang, Z.; Yao, J.; Xiong, L.I. Study on loess landform classification based on random forest. J. Geo Inf. Sci. 2020, 22, 452–463. [Google Scholar]
- Verhagen, P.; Drăguţ, L. Object-based landform delineation and classification from DEMs for archaeological predictive mapping. J. Archaeol. Sci. 2012, 39, 698–703. [Google Scholar] [CrossRef]
- Drăguţ, L.; Eisank, C. Object representations at multiple scales from digital elevation models. Geomorphology 2011, 129, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van der Meer, F.; Van der Werff, H.; Van Coillie, F. Geographic object-based image analysis–towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Weng, Q.; Hay, G.J.; He, Y. Geographic object-based image analysis (GEOBIA): Emerging trends and future opportunities. GIScience Remote. Sens. 2018, 55, 159–182. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.; Tang, G.a.; Zhang, F.; Yang, J. A cellular automata model for simulating the evolution of positive–negative terrains in a small loess watershed. Int. J. Geogr. Inf. Sci. 2013, 27, 1349–1363. [Google Scholar] [CrossRef]
- Huang, S.-L.; Ferng, J.-J. Applied land classification for surface water quality management: II. Land process classification. J. Environ. Manag. 1990, 31, 127–141. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Y. Study on the classification of typical loess geomorphology facing sub-basin units. Arid Zone Res. 2019, 36, 1592–1598. [Google Scholar]
- Caratti, J.F.; Nesser, J.A.; Lee Maynard, C. Watershed classification using canonical correspondence analysis and clustering techniques: A cautionary note 1. J. Am. Water Resour. Assoc. 2004, 40, 1257–1268. [Google Scholar] [CrossRef]
- Monteiro, F.C.; Campilho, A. Watershed framework to region-based image segmentation. In Proceedings of the 2008 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Zuecco, G.; Rinderer, M.; Penna, D.; Borga, M.; Van Meerveld, H. Quantification of subsurface hydrologic connectivity in four headwater catchments using graph theory. Sci. Total Environ. 2019, 646, 1265–1280. [Google Scholar] [CrossRef]
- Rong, J.; Pan, Y.L. Accuracy improvement of graph-cut image segmentation by using watershed. Adv. Mater. Res. 2012, 341, 546–549. [Google Scholar] [CrossRef]
- Pirzada, S.; Dharwadker, A. Applications of graph theory. J. Korean Soc. Ind. Appl. Math. 2007, 7, 2070013. [Google Scholar]
- Phillips, J.D.; Schwanghart, W.; Heckmann, T. Graph theory in the geosciences. Earth Sci. Rev. 2015, 143, 147–160. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [Green Version]
- Poulter, B.; Goodall, J.L.; Halpin, P.N. Applications of network analysis for adaptive management of artificial drainage systems in landscapes vulnerable to sea level rise. J. Hydrol. 2008, 357, 207–217. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Complex-network description of seismicity. Nonlinear Process. Geophys. 2006, 13, 145–150. [Google Scholar] [CrossRef]
- Tian, Z.; Jia, L.m.; Dong, H.h.; Su, F.; Zhang, Z.D. Analysis of Urban Road Traffic Network Based on Complex Network. Procedia Eng. 2016, 137, 537–546. [Google Scholar] [CrossRef] [Green Version]
- Yu, F.; Xue, L.; Sun, C.; Zhang, C. Product transportation distance based supplier selection in sustainable supply chain network. J. Clean. Prod. 2016, 137, 29–39. [Google Scholar] [CrossRef]
- Hossmann, T.; Spyropoulos, T.; Legendre, F. A complex network analysis of human mobility. In Proceedings of the 2011 IEEE Conference on Computer Communications Workshops, Shanghai, China, 10–15 April 2011; pp. 876–881. [Google Scholar]
- Kaluza, P.; Kölzsch, A.; Gastner, M.T.; Blasius, B. The complex network of global cargo ship movements. J. Royal Soc. Interface 2010, 7, 1093–1103. [Google Scholar] [CrossRef]
- Lin, J.; Ban, Y. Complex network topology of transportation systems. Transp. Rev. 2013, 33, 658–685. [Google Scholar] [CrossRef]
- Prabakaran, G.; Vaithiyanathan, D.; Ganesan, M. Application of fuzzy combined SVM & graph theory for agriculture productivity prediction. J. Phys. Conf. Ser. 2020, 1706, 012039. [Google Scholar]
- Cantwell, M.D.; Forman, R.T. Landscape graphs: Ecological modeling with graph theory to detect configurations common to diverse landscapes. Landsc. Ecol. 1993, 8, 239–255. [Google Scholar] [CrossRef]
- Wu, X.; Yu, K.; Wang, X. On the growth of Internet application flows: A complex network perspective. In Proceedings of the 2011 IEEE INFOCOM, Shanghai, China, 10–15 April 2011; pp. 2096–2104. [Google Scholar]
- Gan, C.; Yang, X.; Liu, W.; Zhu, Q.; Jin, J.; He, L. Propagation of computer virus both across the Internet and external computers: A complex-network approach. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2785–2792. [Google Scholar] [CrossRef]
- Heckmann, T.; Schwanghart, W.; Phillips, J.D. Graph theory—Recent developments of its application in geomorphology. Geomorphology 2015, 243, 130–146. [Google Scholar] [CrossRef]
- Beauguitte, L.; Ducruet, C. Scale-free and small-world networks in geographical research: A critical examination. In Proceedings of the 17th European Colloquium on Theoretical and Quantitative Geography, Athens, Greece, 1 September 2011; pp. 663–671. [Google Scholar]
- Suweis, S.; Konar, M.; Dalin, C.; Hanasaki, N.; Rinaldo, A.; Rodriguez-Iturbe, I. Structure and controls of the global virtual water trade network. Geophys. Res. Lett. 2011, 38, L10403. [Google Scholar] [CrossRef] [Green Version]
- Halverson, M.J.; Fleming, S.W. Complex network theory, streamflow, and hydrometric monitoring system design. Hydrol. Earth Syst. Sci. 2015, 19, 3301–3318. [Google Scholar] [CrossRef] [Green Version]
- Rinaldo, A.; Banavar, J.R.; Maritan, A. Trees, networks, and hydrology. Water Resour. Res. 2006, 42, W06D07. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, X.; Xiao, C.; Zhang, Y.; Luo, M. Positive and negative terrains on northern Shaanxi Loess Plateau. J. Geogr. Sci. 2010, 20, 64–76. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, G.; Yan, S.; Zhu, S.; Sun, Y. Landform-oriented flow-routing algorithm for the dual-structure loess terrain based on digital elevation models. Hydrol. Process. 2014, 28, 1756–1766. [Google Scholar] [CrossRef]
- Yang, F.; Zhou, Y. Quantifying spatial scale of positive and negative terrains pattern at watershed-scale: Case in soil and water conservation region on Loess Plateau. J. Mt. Sci. 2017, 14, 1642–1654. [Google Scholar] [CrossRef]
- Tang, G.; Song, X.; Li, F.; Zhang, Y.; Xiong, L. Slope spectrum critical area and its spatial variation in the Loess Plateau of China. J. Geogr. Sci. 2015, 25, 1452–1466. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y. Study on Positive and Negative Topography and Spatial Differentiation of Loess Plateau Based on DEM. Ph.D. Thesis, Nanjing Normal University, Nanjing, China, 2011. [Google Scholar]
- Strahler, A.N. Quantitative slope analysis. Geol. Soc. Am. Bull. 1956, 67, 571–596. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, Y.; Xu, Y.; Liu, H. Hierarchy structure characteristics analysis for the China Loess watersheds based on gully node calibration. J. Mt. Sci. 2018, 15, 2637–2650. [Google Scholar] [CrossRef]
- Li, C.; Li, F.; Dai, Z.; Yang, X.; Cui, X.; Luo, L. Spatial variation of gully development in the loess plateau of China based on the morphological perspective. Earth Sci. Inform. 2020, 13, 1103–1117. [Google Scholar] [CrossRef]
- Wang, K.; Chen, N. Extraction method for terrain feature point considering spatial feature. Sci. Surv. Mapp. 2021, 46, 192–202. [Google Scholar]
- Lai, H.; Bing, X.; Liang, H.; Bi, X.; Yang, Z.; Lu, J. Extraction of River Network in Three Gorges Reservoir Area Based on Mean Change Point Analysis. Sci. Surv. Mapp. 2012, 37, 173–175. [Google Scholar]
- Tucker, G.E.; Bras, R.L. Hillslope processes, drainage density, and landscape morphology. Water Resour. Res. 1998, 34, 2751–2764. [Google Scholar] [CrossRef] [Green Version]
- Wang, T. A Preliminary Study on Population Characteristics of Gullies in Small Watershed of the Loess Plateau. Doctoral Dissertation, Nanjing Normal University, Nanjing, China, 2015. [Google Scholar]
- Zhu, M.; Li, F. Study on the influence of slope classification on surface slope spectrum. Sci. Surv. Mapp. 2009, 34, 165–167. [Google Scholar]
- Dang, X.; Zhou, C.; Wang, B.; Wei, W. Evolution of slope spectrum of construction land in China and influence of slope climbing. Acta Geogr. Sin. 2021, 76, 1747–1762. [Google Scholar]
- Yang, Q.; Wang, C. Study on minimum area threshold for slope statistical analysis. Sci. Surv. Mapp. 2020, 45, 172–177. [Google Scholar]
- Zhao, W.; Dong, Q.; Yan, T.; Qin, W.; Zhu, Q. Analysis of the relationship between slope spectrum information entropy and topographic factors in purple soil water erosion area in southwest China. Trans. Chin. Soc. Agric. Eng. 2020, 36, 160–167. [Google Scholar]
- Zhao, M.; Tang, G.; Chen, Z.; Zhu, H.C. Comparison of different slope classification systems and surface slope spectrum in loess hilly and gully region. Bull. Soil Water Conserv. 2002, 33–36. [Google Scholar]
- Yi, X.; Zhou, F.; Wang, X.; Yang, Y.; Guo, H. Watershed classification and runoff simulation in no data area based on SOM. Progress Geogr. 2014, 33, 1109–1116. [Google Scholar]
- Wu, S.; Rao, L. Characteristics and spatial differentiation of slope spectrum in different types of arsenic sandstone. Trans. Chin. Soc. Agric. Eng. 2021, 37, 125–132. [Google Scholar]
- Tang, G. Exploration and Practice of Digital Terrain Analysis on Loess Plateau; Science Press: Beijing, China, 2015. [Google Scholar]
- Wang, C.; Tang, G.; Li, F.; Zhu, X.; Jia, Y. Uncertainty of slope spectrum information extraction based on DEM. Geoinf. Sci. 2008, 10, 539–544. [Google Scholar] [CrossRef]
- Wang, C.; Tang, G.; Li, F.; Yang, X.; Ge, S. Basic regional conditions for extraction and application of slope spectrum. Sci. Geogr. Sin. 2007, 27, 587–592. [Google Scholar]
- Tang, G.; Zhao, M.; Li, T.; Liu, Y.; Xie, Y. Uncertainty of ground slope in loess Plateau extracted from DEM. Acta Geogr. Sin. 2003, 58, 824–830. [Google Scholar]
- Li, F.; Tang, G.; Wang, C.; Cui, L.; Zhu, R. Slope spectrum variation in a simulated loess watershed. Front. Earth Sci. 2016, 10, 328–339. [Google Scholar] [CrossRef]
- Tang, G.; Na, J.; Cheng, W. Research progress of digital topographic analysis of regional geomorphology in China. Acta Geod. Et Cartogr. Sin. 2017, 46, 1570–1591. [Google Scholar]
- Tang, G.; Li, F. Xiong LI-yang. Research progress of digital topographic analysis on loess Plateau. Geogr. Geo Inf. Sci. 2017, 33, 1–7. [Google Scholar]
- Peng, Q.; Tang, L.; Chen, J.; Chen, Y. Study on slope spectrum evolution of construction land in Shenzhen in 2000 and 2015. J. Nat. Resour. 2018, 33, 2200–2212. [Google Scholar]
- Liu, S.; Li, F.; Jiang, R.; Chang, R.; Liu, W. Automatic identification and analysis of slope spectrum of loess landform types. J. Geo Inf. Sci. 2015, 17, 1234–1242. [Google Scholar]
- Li, H.; Wu, J.; Wang, X. Object-oriented land use classification in Dongjiang River Basin based on GF-1 image. Trans. Chin. Soc. Agric. Eng. 2018, 34, 245–252. [Google Scholar]
- Li, F.; Tang, G.; Jia, P.; Cao, Z. Scale effect and spatial differentiation of slope spectrum information entropy. Geoinf. Sci. 2007, 9, 13–18. [Google Scholar] [CrossRef]
- Ju, Z.; Zhang, J.; Bai, Z. Study on the relationship between information entropy of mountain slope spectrum and topographic factors of soil and water loss. Sci. Surv. Mapp. 2019, 44, 86–90. [Google Scholar]
- Chu, Y.; Zhu, L.; Tang, B.; Li, X. Characteristics of surface slope spectrum in the upper reaches of Shule River basin. Arid Land Geogr. 2015, 38, 345–350. [Google Scholar]
- Chen, J.; Zou, Y. Study on soil and water conservation based on slope spectrum and information entropy: A case study of three counties in Hunan Province. Geomat. Spat. Inf. 2016, 39, 97–101. [Google Scholar]
- Zhao, S.; Cheng, W. Transitional relation exploration for typical loess geomorphologic types based on slope spectrum characteristics. Earth Surf. Dyn. 2014, 2, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative Analysis of Land Surface Topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Tang, G.; Li, F.; Liu, X.; Long, Y.; Yang, X. Research on the slope spectrum of the Loess Plateau. Sci. China Ser. E Technol. Sci. 2008, 51, 175–185. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, G.; Li, F.; Xiong, L. Review of research along loess landform gully. Geogr. Geo Inf. Sci. 2012, 28, 44–48. [Google Scholar]
- Zhou, Y.; Tang, G.; Wang, C.; Xiao, C.; Dong, Y.; Sun, J. Study on automatic segmentation of positive and negative terrain of loess landform based on high-resolution DEM. Sci. Geogr. Sin. 2010, 30, 261–266. [Google Scholar]
- Zhu, H.; Tang, G.; Zhang, Y.; Yi, H.; Li, M. Extraction of gully line in loess hilly region based on DEM. Bull. Soil Water Conserv. 2003, 43–45. [Google Scholar]
- Tang, G.; Yang, X. ArcGIS Gis Spatial Analysis Experiment Course; Version 2; Science Press: Bejing, China, 2012. [Google Scholar]
- Lu, Z. Watershed Geomorphic System; Dalian Press: Dalian, China, 1991. [Google Scholar]
- Zhou, C.; Cheng, W.; Qian, J.; Li, B.; Zhang, B. Study on the classification system of 11 million digital landforms in China. J. Geo Inf. Sci. 2009, 11, 707–724. [Google Scholar]
- Zhu, H.; Tang, G.; Wu, L.; Qian, K. Extraction and analysis of gully nodes based on geomorphological structures and catchment characteristics: A case study in the Loess Plateau of north Shaanxi province. Adv. Water Sci. 2012, 23, 7–13. [Google Scholar]
- Tricot, C. Curves and Fractal Dimension; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Zhang, J.; Mucs, D.; Norinder, U.; Svensson, F. LightGBM: An effective and scalable algorithm for prediction of chemical toxicity–application to the Tox21 and mutagenicity data sets. J. Chem. Inf. modeling 2019, 59, 4150–4158. [Google Scholar] [CrossRef] [PubMed]
- Al Daoud, E. Comparison between XGBoost, LightGBM and CatBoost using a home credit dataset. Int. J. Comput. Inf. Eng. 2019, 13, 6–10. [Google Scholar]
- Chen, X.; Hu, J.; Chen, X.; Zhang, W. Simulation and effectiveness evaluation of network warfare based on LightGBM algorithm. J. Comput. Appl. 2020, 40, 2003–2008. [Google Scholar]
- Wang, D.; Zhang, Y.; Zhao, Y. LightGBM: An effective miRNA classification method in breast cancer patients. In Proceedings of the 2017 International Conference on Computational Biology and Bioinformatics, Budapest, Hungary, 18 October 2017; pp. 7–11. [Google Scholar]
- Syarif, I.; Prugel-Bennett, A.; Wills, G. SVM parameter optimization using grid search and genetic algorithm to improve classification performance. Telkomnika 2016, 14, 1502. [Google Scholar] [CrossRef]
- Lerman, P. Fitting segmented regression models by grid search. J. R. Stat. Soc. Ser. C 1980, 29, 77–84. [Google Scholar] [CrossRef]
- Dietterich, T.G. Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput. 1998, 10, 1895–1923. [Google Scholar] [CrossRef] [Green Version]
- Mei, Z.; Xiang, F.; Zhen-hui, L. Short-term traffic flow prediction based on combination model of xgboost-lightgbm. In Proceedings of the 2018 International Conference on Sensor Networks and Signal Processing (SNSP), Xi’an, China, 1 October 2018; pp. 322–327. [Google Scholar]
- Ma, X.; Sha, J.; Wang, D.; Yu, Y.; Yang, Q.; Niu, X. Study on a prediction of P2P network loan default based on the machine learning LightGBM and XGboost algorithms according to different high dimensional data cleaning. Electron. Commer. Res. Appl. 2018, 31, 24–39. [Google Scholar] [CrossRef]
- Li, F.; Tang, G.; Wang, C.; Zhang, T. Quantitative analysis and spatial distribution of slope spectrum: A case study in the Loess Plateau in north Shaanxi province. Geoinformatics 2007 Geospat. Inf. Sci. 2007, 6753, 67531R. [Google Scholar] [CrossRef]
- Zhang, L. Study on Spatial Pattern of Loess Landform Based on Core Topographic Factor Analysis. Master’s Thesis, Nanjing Normal University, Nanjing, China, 2013. [Google Scholar]
- Zhang, W. Study on the Watershed Profile Spectrum of Loess Plateau in Northern Shaanxi Based on DEM. Master’s Thesis, Nanjing Normal University, Nanjing, China, 2011. [Google Scholar]
- Zhu, S. Study on the Elevation Integral Pedigree of Loess Plateau Watershed Area Based on DEM. Ph.D. Thesis, Nanjing Normal University, Nanjing, China, 2013. [Google Scholar]
- Guth, P.L. Quantifying and visualizing terrain fabric from Digital Elevation Models. In Proceedings of the Geocomputacion 99: Proceedings of the 4th International Conference of GeoComputacion, Fredericksburg, VA, USA, 1 January 1999. [Google Scholar]
- Sivakumar, B.; Puente, C.E.; Maskey, M.L. Complex Networks and Hydrologic Applications. In Advances in Nonlinear Geosciences; Springer: Cham, Switzerland, 2018; pp. 565–586. [Google Scholar] [CrossRef]















| Area Name | Area Name | Center Latitude and Longitude | Landform Type | Development Stage |
|---|---|---|---|---|
| I | Shenmu | 110°29′56.040″ N 38°50′32.424″ E | Loess deep incision gorge-hill | submature stage |
| II | Suide | 110°18′45.000″ N 37°35′00.000″ E | Loess hill-ridge | late mature stage |
| III | Dingbian | 107°35′52.548″ N 37°35′25.332″ E | Loess ridge-tableland | submature stage |
| IV | Ansai | 109°21′00.000″ N 36°50′30.000″ E | Loess hill | late mature stage |
| V | Yanchuan | 109°56′15.000″ N 36°45′00.000″ E | Loess hill-ridge | late mature stage |
| VI | Fuxian | 109°33′45.000″ N 36°12′30.000″ E | Loess hill-ridge | late mature stage |
| VII | Yijun | 109°22′30.000″ N 35°27′30.000″ E | Loess ridge | submature stage |
| VIII | Changwu | 107°47′42.360″ N 35°12′24.120″ E | Loess tableland | infancy stage |
| IX | Chunhua | 108°26′15.000″ N 34°52′30.000″ E | Loess middle-low mountain, loess platform-tableland | infancy stage |
| Quantitative Indexes | Algorithm | Remark |
|---|---|---|
| Average node strength (NS) | is the edge weight (height differences) between node and node ; is the element of the network adjacency matrix | |
| Average path length (AL) | is the total number of the nodes in the network; is the distance between node and node j (i.e., the sum number of edges in the shortest path of two nodes); | |
| Fractal dimension (FD) | Box dimension method is a common and effective approach [104]. For any watershed network, we used the box whose length is r to cover it. We computed the number of nonempty boxes (t(r)) with the case that watershed under setting different lengths (r = 1, 2, 3, 4, …, M). By defining r as the x-axis and as the y-axis, least-square method was utilized to conduct linear regression. The negative slope for the fitted equation is the fractal dimension. | |
| structure entropy (SE) | is the importance of i-th node; is the total number of the network node; is the degree of the i-th node. | |
| network density (ND) | m is the actual number of connected edges in the network; is the sum number of the nodes; | |
| Modularity (M) | is the total edges of the network; is the sum of the weights for node ; represents the weight of the edge between node and node ; is the function that set = 1 when a = b, otherwise = 0; is the community to which node belonged. | |
| gully line density | GL is the gully line density, is the total length of the gully lines in the sample area, is the watershed area. |
| Quantitative Indexes | Algorithm | Remark |
|---|---|---|
| Extent for nibbling away () | is the horizontal projection area of the negative terrain; is the horizontal projection area of the positive terrain | |
| Cutting Depth () | is the height of the positive terrain; is the height of the negative terrain; | |
| Shape Metrics () | is the shape metric; is area weight of the -th patch; is area of the -th patch; is the perimeter of the -th patch | |
| Homogeneous index () | is the number of positive patch; is the area of each positive patch; | |
| Fragmentation () | is the number of positive patch; is the area of each positive patch; | |
| Mean-Slope-Difference () | is the slope of the positive terrain; is the slope of the negative terrain; |
| Loess Tableland | Loess Ridge | Loess Hill | Stony Mountain | Sand Hill | Valley Plain | Precision (%) | Recall Rate (%) | F1 (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Loess tableland | 10 | 0 | 0 | 0 | 0 | 0 | 90.9 | 100 | 95.45 |
| Loess ridge | 0 | 10 | 0 | 0 | 0 | 0 | 90.9 | 100 | 95.45 |
| Loess hill | 0 | 0 | 10 | 0 | 0 | 0 | 100 | 100 | 100 |
| Stony mountain | 0 | 1 | 0 | 9 | 0 | 0 | 90 | 90 | 90 |
| sand hill | 1 | 0 | 0 | 0 | 8 | 1 | 80 | 80 | 80 |
| valley plain | 0 | 0 | 0 | 0 | 2 | 8 | 88.9 | 80 | 84.45 |
| Overall accuracy, 91.67% | |||||||||
| Kappa coefficient, 0.9004 | |||||||||
| Loess Tableland | Loess Ridge | Loess Hill | Stony Mountain | Sand Hill | Valley Plain | Precision (%) | Recall Rate (%) | F1 (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Loess tableland | 9 | 1 | 0 | 0 | 1 | 0 | 90 | 90 | 90 |
| Loess ridge | 1 | 8 | 1 | 0 | 0 | 0 | 66.67 | 80 | 73.34 |
| Loess hill | 0 | 2 | 8 | 0 | 0 | 0 | 88.89 | 80 | 84.45 |
| Stony mountain | 0 | 1 | 0 | 9 | 0 | 0 | 90 | 90 | 90 |
| sand hill | 1 | 0 | 0 | 0 | 8 | 1 | 88.89 | 80 | 84.4 |
| valley plain | 0 | 0 | 0 | 1 | 0 | 9 | 90 | 90 | 90 |
| Overall accuracy, 86.67% | |||||||||
| Kappa coefficient, 0.8404 | |||||||||
| Loess Tableland | Loess Ridge | Loess Hill | Stony Mountain | Sand Hill | Valley Plain | Total Accuracy | |
|---|---|---|---|---|---|---|---|
| LightGBM | 95.45 | 95.45 | 100 | 90 | 80 | 84.45 | 91.67 |
| RF | 95 | 90 | 90 | 90 | 80 | 84.44 | 88.34 |
| XGBoost | 95.45 | 90.91 | 95 | 90 | 90 | 84.45 | 90 |
| GBDT | 90 | 90 | 90 | 84.44 | 85.91 | 80 | 86.67 |
| SVM | 90 | 85.91 | 90 | 90 | 85.91 | 80.00 | 86.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Chen, N.; He, Z. Automatic Landform Recognition from the Perspective of Watershed Spatial Structure Based on Digital Elevation Models. Remote Sens. 2021, 13, 3926. https://doi.org/10.3390/rs13193926
Lin S, Chen N, He Z. Automatic Landform Recognition from the Perspective of Watershed Spatial Structure Based on Digital Elevation Models. Remote Sensing. 2021; 13(19):3926. https://doi.org/10.3390/rs13193926
Chicago/Turabian StyleLin, Siwei, Nan Chen, and Zhuowen He. 2021. "Automatic Landform Recognition from the Perspective of Watershed Spatial Structure Based on Digital Elevation Models" Remote Sensing 13, no. 19: 3926. https://doi.org/10.3390/rs13193926
APA StyleLin, S., Chen, N., & He, Z. (2021). Automatic Landform Recognition from the Perspective of Watershed Spatial Structure Based on Digital Elevation Models. Remote Sensing, 13(19), 3926. https://doi.org/10.3390/rs13193926