Sub-Pixel Mapping Model Based on Total Variation Regularization and Learned Spatial Dictionary
Abstract
:1. Introduction
2. Sub-Pixel Mapping Model
2.1. Mathematical Notation
| Notation | Description |
| norm p | |
| u | the input data, and abundances fractions of classes. |
| abundances fraction of class c or low spatial resolution image of class c. | |
| high spatial resolution image of class c. | |
| X | sub-pixel mapping result or high spatial resolution image with non-smooth edges. |
| final sub-pixel mapping result or high spatial resolution image with smooth edges. | |
| E | down-sampling vector or matrix. |
| D | spatial dictionary. |
| and | sparse coefficients. |
| S | scale factor. |
| TV | Total Variation |
| ITV | Isotropic Total Variation |
2.2. Sub-Pixel Mapping Definition
2.3. Sub-Pixel Mapping Model
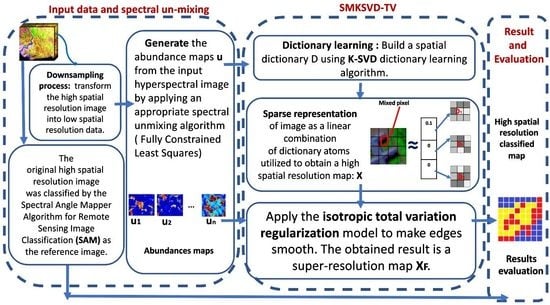
3. Method
- A downsampling step: It was applied to high spatial resolution image in order to provide an image with coarse spatial resolution. Then, the low spatial resolution map is used as the input of spectral un-mixing step.
- Generate the abundance maps u from the input hyperspectral image by applying an appropriate spectral unmixing algorithm (in our study, we used a fully-constraint Least Square algorithm).
- Dictionary learning: Build a spatial dictionary D using K-SVD dictionary learning algorithm.
- Sparse representation of image as a linear combination of dictionary atoms utilized to obtain a high spatial resolution map: X.
- Apply the total variation regularization model to make edges smooth. The obtained result is a super-resolution map .
3.1. Dictionary Learning
- q is the number of small image patches. It is larger than k.
- k is the number of atoms in the incomplete dictionary.
- D is the dictionary shown in Figure 3.
- is the sparse coefficient of jth signal.
- k is the number of atoms in the dictionary.
- .
- q the number of signals.
- Initialize the dictionary: k signals were picked randomly from q signals of z.
- Sparse coding: Given the dictionary, the sparse code for each signal was obtained. For every signal, the sparse code was provided.
- Update the dictionary: As the sparse code is known, we update the dictionary D and the atoms one by one. We picked randomly one atom at a time and all the signals using it to make it more appropriate for these signals.is the error, denotes the Frobenius norm, and designates an atom.
- Repeat step 2 and step 3 until a prefix number of iterations is obtained.
3.2. Sparse Modeling of High Spatial Resolution Data Using the Dictionary
- ,
- ,
- is the down-sampling matrix, and
- is the learned spatial dictionary, using K-SVD dictionary learning algorithm. D1, D2, D3, D4, D5, and D6 represent examples of the dictionary atoms shown in Figure 3. The size of each atom in the dictionary D is equal to , where Di designates a spatial patch, and X corresponds to the ( sub-pixels) sub-pixel mapping result.
3.3. Spatial Regularization Using Isotropic Total Variation
- The first component is called the error term. In our study, it relates two fine spatial resolution images.
- The second component, named the prior regularization term , is the main element used in the proposed formulation.
4. Experimental Results
4.1. Example 1: Jasper Ridge Hyperspectral Image
4.1.1. Quantitative Analysis
4.1.2. Sensitivity Analysis
4.2. Example 2: Pavia University
4.3. Example 3: Hydice Urban Hyperspectral Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPM | Sub-Pixel Mapping |
| TV | Total Variation |
| Er | Error |
| SAM | Spectral Angle Mapper |
| FCLS | Fully Constraint Least Square |
| K-SVD | K-Singular Value Decomposition |
| DCT | Discret Cosine Transform |
| SMKSVD-TV | Sub-pixel Mapping K-Singular Value Decomposition-Total Variation |
| CNN-like | Convolutional Neural Networks-like |
| MAP | Maximum A Posteriori |
References
- Kaur, S.; Bansal, R.; Mittal, M.; Goyal, L.M.; Kaur, I.; Verma, A. Mixed pixel decomposition based on extended fuzzy clustering for single spectral value remote sensing images. J. Indian Soc. Remote Sens. 2019, 47, 427–437. [Google Scholar] [CrossRef]
- Tatem, A.J.; Lewis, H.G.; Atkinson, P.M.; Nixon, M.S. Multiple-class land-cover mapping at the sub-pixel scale using a Hopfield neural network. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 184–190. [Google Scholar] [CrossRef]
- Su, Y.F.; Foody, G.M.; Muad, A.M.; Cheng, K.S. Combining Hopfield neural network and contouring methods to enhance super-resolution mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1403–1417. [Google Scholar]
- Genitha, C.H.; Vani, K. Super resolution mapping of satellite images using Hopfield neural networks. In Recent Advances in Space Technology Services and Climate Change (RSTSCC); IEEE: Piscataway, NJ, USA, 2010; pp. 114–118. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef] [Green Version]
- Prades, J.; Safont, G.; Salazar, A.; Vergara, L. Estimation of the Number of Endmembers in Hyperspectral Images Using Agglomerative Clustering. Remote Sens. 2020, 12, 3585. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Q.; Xue, X.; Ha, M.; Ma, L.; Zhang, X.; Yu, Z. Possibility measure based fuzzy support function machine for set-based fuzzy classifications. Inf. Sci. 2019, 483, 192–205. [Google Scholar] [CrossRef]
- Atkinson, P.M. Mapping sub-pixel boundaries from remotely sensed images. Innov. GIS 1997, 4, 166–180. [Google Scholar]
- Vikhamar, D.; Solberg, R. Subpixel mapping of snow cover in forests by optical remote sensing. Remote Sens. Environ. 2003, 84, 69–82. [Google Scholar] [CrossRef]
- Lv, Y.; Gao, W.; Yang, C.; Fang, Z. A novel spatial–spectral extraction method for subpixel surface water. Int. J. Remote Sens. 2020, 41, 2477–2499. [Google Scholar] [CrossRef]
- Ling, F.; Du, Y.; Zhang, Y.; Li, X.; Xiao, F. Burned-area mapping at the subpixel scale with MODIS images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1963–1967. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, K.; Zhong, Y.; Li, P. A new sub-pixel mapping algorithm based on a BP neural network with an observation model. Neurocomputing 2008, 71, 2046–2054. [Google Scholar] [CrossRef]
- Thornton, M.; Atkinson, P.M.; Holland, D. A linearised pixel-swapping method for mapping rural linear land cover features from fine spatial resolution remotely sensed imagery. Comput. Geosci. 2007, 33, 1261–1272. [Google Scholar] [CrossRef]
- Song, M.; Zhong, Y.; Ma, A.; Xu, X.; Zhang, L. Multiobjective Subpixel Mapping With Multiple Shifted Hyperspectral Images. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 8176–8191. [Google Scholar] [CrossRef]
- Msellmi, B.; Picone, D.; Rabah, Z.B.; Dalla Mura, M.; Farah, I.R. Sub-pixel Mapping Method based on Total Variation Minimization and Spectral Dictionary. In Proceedings of the 2020 5th International Conference on Advanced Technologies for Signal and Image Processing (ATSIP), Sousse, Tunisia, 2–5 September 2020. [Google Scholar]
- Chen, Y.; Ge, Y.; Chen, Y.; Jin, Y.; An, R. Subpixel Land Cover Mapping Using Multiscale Spatial Dependence. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 5097–5106. [Google Scholar] [CrossRef]
- Wu, S.; Chen, Z.; Ren, J.; Jin, W.; Hasituya; Guo, W.; Yu, Q.; others. An Improved Subpixel Mapping Algorithm Based on a Combination of the Spatial Attraction and Pixel Swapping Models for Multispectral Remote Sensing Imagery. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1070–1074. [Google Scholar] [CrossRef]
- Wu, S.; Ren, J.; Chen, Z.; Jin, W.; Liu, X.; Li, H.; Pan, H.; Guo, W. Influence of reconstruction scale, spatial resolution and pixel spatial relationships on the sub-pixel mapping accuracy of a double-calculated spatial attraction model. Remote Sens. Environ. 2018, 210, 345–361. [Google Scholar] [CrossRef]
- Wang, P.; Wu, Y.; Leung, H. Subpixel land cover mapping based on a new spatial attraction model with spatial-spectral information. Int. J. Remote. Sens. 2019, 40, 1–20. [Google Scholar] [CrossRef]
- Wang, Q.; Atkinson, P.M.; Shi, W. Indicator cokriging-based subpixel mapping without prior spatial structure information. IEEE Trans. Geosci. Remote Sens. 2014, 53, 309–323. [Google Scholar] [CrossRef]
- Liu, Q.; Trinder, J. Subpixel Mapping of Multispectral Images Using Markov Random Field with Graph Cut Optimization. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1507–1511. [Google Scholar] [CrossRef]
- Zhao, J.; Zhong, Y.; Wu, Y.; Zhang, L.; Shu, H. Sub-pixel mapping based on conditional random fields for hyperspectral remote sensing imagery. IEEE J. Sel. Top. Signal Process. 2015, 9, 1049–1060. [Google Scholar] [CrossRef]
- Tiwari, L.; Sinha, S.; Saran, S.; Tolpekin, V.; Raju, P. Markov random field-based method for super-resolution mapping of forest encroachment from remotely sensed ASTER image. Geocarto Int. 2016, 31, 428–445. [Google Scholar] [CrossRef]
- Zhong, Y.; Cao, Q.; Zhao, J.; Ma, A.; Zhao, B.; Zhang, L. Optimal decision fusion for urban land-use/land-cover classification based on adaptive differential evolution using hyperspectral and LiDAR data. Remote Sens. 2017, 9, 868. [Google Scholar] [CrossRef] [Green Version]
- Tong, X.; Xu, X.; Plaza, A.; Xie, H.; Pan, H.; Cao, W.; Lv, D. A new genetic method for subpixel mapping using hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4480–4491. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Li, Z. Land cover change detection at subpixel resolution with a Hopfield neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1339–1352. [Google Scholar] [CrossRef]
- Arun, P.; Buddhiraju, K.M.; Porwal, A. Integration of contextual knowledge in unsupervised subpixel classification: Semivariogram and pixel-affinity based approaches. IEEE Geosci. Remote Sens. Lett. 2018, 15, 262–266. [Google Scholar] [CrossRef]
- Wang, P.; Wang, L.; Wu, Y.; Leung, H. Utilizing Pansharpening Technique to Produce Sub-Pixel Resolution Thematic Map from Coarse Remote Sensing Image. Remote Sens. 2018, 10, 884. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, M.Q.; Atkinson, P.M.; Lewis, H.G. Superresolution mapping using a Hopfield neural network with fused images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 736–749. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Dalla Mura, M.; Chanussot, J.; Zhang, G. Soft-then-hard super-resolution mapping based on pansharpening technique for remote sensing image. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 334–344. [Google Scholar] [CrossRef]
- Xu, X.; Zhong, Y.; Zhang, L. A sub-pixel mapping method based on an attraction model for multiple shifted remotely sensed images. Neurocomputing 2014, 134, 79–91. [Google Scholar] [CrossRef]
- Wang, P.; Wang, L.; Dalla Mura, M.; Chanussot, J. Using Multiple Subpixel Shifted Images with Spatial–Spectral Information in Soft-Then-Hard Subpixel Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2950–2959. [Google Scholar] [CrossRef]
- Zhong, Y.; Wu, Y.; Xu, X.; Zhang, L. An adaptive subpixel mapping method based on MAP model and class determination strategy for hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1411–1426. [Google Scholar] [CrossRef]
- Feng, R.; He, D.; Zhong, Y.; Zhang, L. Sparse representation based subpixel information extraction framework for hyperspectral remote sensing imagery. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 7026–7029. [Google Scholar]
- Feng, R.; Zhong, Y.; Xu, X.; Zhang, L. Adaptive sparse subpixel mapping with a total variation model for remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2855–2872. [Google Scholar] [CrossRef]
- Xu, X.; Zhong, Y.; Zhang, L. Adaptive subpixel mapping based on a multiagent system for remote-sensing imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 787–804. [Google Scholar] [CrossRef]
- Msellmi, B.; Rabah, Z.B.; Farah, I.R. A graph based model for sub-pixel objects recognition. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7070–7073. [Google Scholar]
- Xu, Y.; Huang, B. A spatio–temporal pixel-swapping algorithm for subpixel land cover mapping. IEEE Geosci. Remote Sens. Lett. 2014, 11, 474–478. [Google Scholar] [CrossRef]
- Mertens, K.C.; De Baets, B.; Verbeke, L.P.; De Wulf, R.R. A sub-pixel mapping algorithm based on sub-pixel/pixel spatial attraction models. Int. J. Remote Sens. 2006, 27, 3293–3310. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, Y.; Stein, A.; Li, S.; Hu, J. Enhanced subpixel mapping with spatial distribution patterns of geographical objects. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2356–2370. [Google Scholar] [CrossRef]
- Helin, P.; Astola, P.; Rao, B.; Tabus, I. Minimum description length sparse modeling and region merging for lossless plenoptic image compression. IEEE J. Sel. Top. Signal Process. 2017, 11, 1146–1161. [Google Scholar] [CrossRef]
- Yang, Y.; Nagarajaiah, S. Structural damage identification via a combination of blind feature extraction and sparse representation classification. Mech. Syst. Signal Process. 2014, 45, 1–23. [Google Scholar] [CrossRef]
- Condat, L. Discrete total variation: New definition and minimization. SIAM J. Imaging Sci. 2017, 10, 1258–1290. [Google Scholar] [CrossRef] [Green Version]
- Zeng, S.; Zhang, B.; Gou, J.; Xu, Y. Regularization on Augmented Data to Diversify Sparse Representation for Robust Image Classification. IEEE Trans. Cybern. 2020, 1–14. [Google Scholar] [CrossRef]
- Zhou, J.; Zeng, S.; Zhang, B. Two-stage knowledge transfer framework for image classification. Pattern Recognit. 2020, 107, 107529. [Google Scholar] [CrossRef]
- Arun, P.; Buddhiraju, K.M.; Porwal, A. CNN based sub-pixel mapping for hyperspectral images. Neurocomputing 2018, 311, 51–64. [Google Scholar] [CrossRef]
- Heylen, R.; Burazerovic, D.; Scheunders, P. Fully constrained least squares spectral unmixing by simplex projection. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4112–4122. [Google Scholar] [CrossRef]













| Predicted Classes | ||||
|---|---|---|---|---|
| Road | Tree | Water | Soil | |
| Road | 3090 | 405 | 348 | 5958 |
| Tree | 3261 | 70 | 48 | 6422 |
| Water | 1899 | 421 | 555 | 2926 |
| Soil | 492 | 163 | 108 | 9038 |
| Road | Tree | Water | Soil | |
|---|---|---|---|---|
| AMCDSM-TV | 03.72 | 02.03 | 34.42 | 33.74 |
| AMCDSM-L | 12.58 | 02.79 | 33.04 | 30.87 |
| ASSM-TV | 13.23 | 03.21 | 33.25 | 31.83 |
| SMKSVD-TV | 10.12 | 01.45 | 22.62 | 18.00 |
| Averege Accuracy (%) | Kappa Coefficients (%) | Overall Accuracy (%) | Computational Time (s) | |
|---|---|---|---|---|
| AMCDSM-TV | 79.02 | 56.63 | 83.73 | 11.87 |
| AMCDSM-L | 80.18 | 58.30 | 84.37 | 13.13 |
| ASSM-TV | 79.62 | 57.01 | 83.88 | 21.03 |
| SMKSVD-TV | 89.19 | 79.19 | 86.95 | 23.70 |
| AMCDSM-TV | AMCDSM-L | ASSM-TV | SMKSVD-TV |
|---|---|---|---|
| Kappa Coefficient (%) | Overall Accuracy (%) | |
|---|---|---|
| AMCDSM-TV | 54.41 | 86.04 |
| AMCDSM-L | 47.99 | 85.78 |
| ASSM-TV | 47.50 | 85.58 |
| SMKSVD-TV | 56.44 | 86.55 |
| Shadow | Unclassified | Asphalt | Meadows | Gravel | Trees | Bare Soil | Bitumen | Brick | |
|---|---|---|---|---|---|---|---|---|---|
| AMCDSM-TV | 6.90 | 43.01 | 7.27 | 34.75 | 61.03 | 3.00 | 19.71 | 49.37 | 47.37 |
| AMCDSM-L | 8.81 | 51.66 | 9.58 | 35.87 | 80.39 | 3.48 | 26.05 | 77.48 | 75.14 |
| ASSM-TV | 9.25 | 51.59 | 9.59 | 35.82 | 77.35 | 3.53 | 26.28 | 75.06 | 73.09 |
| SMKSVD-TV | 7.51 | 52.51 | 10.11 | 7.27 | 80.27 | 3.59 | 29.72 | 89.49 | 78.42 |
| Shadow | Unclassified | Asphalt | Meadows | Gravel | Trees | Bare Soil | Bitumen | Brick | |
|---|---|---|---|---|---|---|---|---|---|
| AMCDSM-TV | 21.60 | 1.40 | 0.28 | 0.74 | 0.84 | 0.25 | 0.31 | 1.00 | 0.32 |
| AMCDSM-L | 28.39 | 1.60 | 0.38 | 0.78 | 1.07 | 0.32 | 0.38 | 1.51 | 0.53 |
| ASSM-TV | 27.92 | 1.65 | 0.37 | 0.81 | 1.17 | 0.33 | 0.42 | 1.60 | 0.55 |
| SMKSVD-TV | 28.86 | 1.22 | 0.42 | 0.44 | 0.69 | 0.34 | 0.40 | 1.16 | 0.52 |
| Predicted Classes | ||||||
|---|---|---|---|---|---|---|
| Concret Road | Ashpalt Road | Grass | Tree | Roof1 | Roof2 | |
| Concret road | 16395 | 361 | 502 | 510 | 42 | 581 |
| Ashpalt road | 447 | 29195 | 2029 | 109 | 32 | 909 |
| Grass | 287 | 1649 | 18430 | 387 | 131 | 257 |
| Tree | 458 | 85 | 694 | 5382 | 70 | 70 |
| Roof1 | 84 | 26 | 268 | 81 | 1888 | 47 |
| Roof2 | 730 | 973 | 276 | 65 | 25 | 6525 |
| Averege Accuracy (%) | Kappa Coefficients (%) | Overall Accuracy (%) | |
|---|---|---|---|
| SMKSVD-TV | 83.33 | 51.26 | 86.46 |
| Concret Road | Ashpalt Road | Grass | Tree | Roof1 | Roof2 | |
|---|---|---|---|---|---|---|
| AMCDSM-TV | 14.44 | 13.03 | 15.29 | 28.01 | 37.68 | 33.14 |
| AMCDSM-L | 14.22 | 13.25 | 15.43 | 28.45 | 35.09 | 30.87 |
| ASSM-TV | 14.76 | 14.33 | 16.35 | 30.66 | 35.42 | 32.63 |
| SMKSVD-TV | 10.85 | 10.78 | 12.82 | 20.73 | 21.14 | 24.07 |
| Concret Road | Ashpalt Road | Grass | Tree | Roof1 | Roof2 | |
|---|---|---|---|---|---|---|
| AMCDSM-TV | 04.01 | 06.84 | 07.22 | 01.83 | 00.61 | 02.43 |
| AMCDSM-L | 04.12 | 06.44 | 07.11 | 01.74 | 00.57 | 02.64 |
| ASSM-TV | 05.10 | 06.79 | 07.53 | 01.82 | 00.58 | 02.70 |
| SMKSVD-TV | 02.80 | 05.40 | 05.47 | 01.83 | 00.34 | 02.29 |
| Concret Road | Ashpalt Road | Grass | Tree | Roof1 | Roof2 | |
|---|---|---|---|---|---|---|
| AMCDSM-TV | 85.55 | 86.96 | 84.71 | 71.99 | 62.32 | 66.86 |
| AMCDSM-L | 85.77 | 86.74 | 84.56 | 71.54 | 64.91 | 69.13 |
| ASSM-TV | 85.24 | 85.66 | 83.64 | 69.34 | 64.57 | 67.37 |
| SMKSVD-TV | 89.14 | 89.22 | 87.17 | 79.62 | 78.86 | 75.92 |
| AMCDSM-TV | AMCDSM-L | ASSM-TV | SMKSVD-TV | |
|---|---|---|---|---|
| Jasper ridge | 83.73 | 84.37 | 83.88 | 86.95 |
| Urban | 82.45 | 82.63 | 81.57 | 86.46 |
| Pavia university | 89.04 | 85.78 | 85.58 | 86.55 |
| Average OA | 85.07 | 84.26 | 83.67 | 86.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Msellmi, B.; Picone, D.; Ben Rabah, Z.; Dalla Mura, M.; Farah, I.R. Sub-Pixel Mapping Model Based on Total Variation Regularization and Learned Spatial Dictionary. Remote Sens. 2021, 13, 190. https://doi.org/10.3390/rs13020190
Msellmi B, Picone D, Ben Rabah Z, Dalla Mura M, Farah IR. Sub-Pixel Mapping Model Based on Total Variation Regularization and Learned Spatial Dictionary. Remote Sensing. 2021; 13(2):190. https://doi.org/10.3390/rs13020190
Chicago/Turabian StyleMsellmi, Bouthayna, Daniele Picone, Zouhaier Ben Rabah, Mauro Dalla Mura, and Imed Riadh Farah. 2021. "Sub-Pixel Mapping Model Based on Total Variation Regularization and Learned Spatial Dictionary" Remote Sensing 13, no. 2: 190. https://doi.org/10.3390/rs13020190
APA StyleMsellmi, B., Picone, D., Ben Rabah, Z., Dalla Mura, M., & Farah, I. R. (2021). Sub-Pixel Mapping Model Based on Total Variation Regularization and Learned Spatial Dictionary. Remote Sensing, 13(2), 190. https://doi.org/10.3390/rs13020190