Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China
Abstract
:1. Introduction
2. Study Area and Accessible Data
2.1. Description of Study Area
2.2. Preparation of the Database
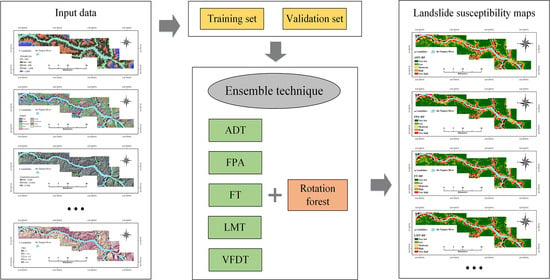
3. Methodology
- (1)
- Data acquisition and preprocessing. In this work, historical landslide events and landslide conditioning factors are acquired to perform spatial prediction of landslide occurrence. Specifically, the historical landslide locations are produced by past landslide records and remote sensing images. Meanwhile, a series of related conditioning factors are selected for LSM and screened using the GR method. Afterwards, these data are resampled with the same grid size. Finally, the training and validation sets are produced for constructing and testing landslide prediction methods.
- (2)
- Construct prediction methods and produce landslide susceptibility maps. The ensemble framework is first performed to optimize the original datasets using the training set. Then, the base classifier of DT is applied to the screened datasets for spatial prediction of landslides. Next, the RF ensemble technique is used for landslide susceptibility modeling. Finally, landslide susceptibility maps are obtained using the constructed prediction methods.
- (3)
- Verification and comparison. The predictive performance of the proposed ensemble framework is evaluated using the objective criteria of ROC and AUC.
3.1. Gain Ratio Method
3.2. Decision Tree Base Classifiers
3.2.1. Alternating Decision Tree
3.2.2. Forest by Penalizing Attributes
3.2.3. Functional Tree
3.2.4. Logistic Model Tree
3.2.5. Hoeffding Tree
3.3. Rotation Forest Ensemble
- (1)
- To construct the training set for the RF algorithm, the feature set with n features is randomly divided into K subsets, and thus each feature subset consists of features.
- (2)
- To apply the feature selection algorithm of principle component analysis (PCA) on each feature subset and obtain a series of principle components (PCs) of (i = 1, 2, …, M; j = 1, 2, …, K).
- (3)
- Repeat the previous steps to obtain the K sets of PC coefficients and put these PC coefficients into the Matrix R as follows:
- (4)
- Multiply the original dataset X with this Matrix (5) to obtain the new feature dataset and the base classifier is trained using this feature dataset.
- (5)
- Repeat the previous steps to obtain trained base classifiers.
- (6)
- For a given unknown sample for prediction, each base classifier produces a class probability value, and all the class probabilities are combined to obtain the final prediction probability.
3.4. Model Evaluation Criteria
4. Results
4.1. Analysis of Landslide Conditioning Factors
4.1.1. Importance Evaluation of Landslide Conditioning Factors
4.1.2. Conditioning Factors Analyses Using Frequency Ratio
4.2. Model Validation
4.3. Comparation with Benchmark Methods
4.4. Parameter Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Factors | Class | No. of Landslide | Percentage of Landslide % | No. of Pixels in Domain | Percentage of Domain % | FR |
|---|---|---|---|---|---|---|
| Altitude (m) | <300 | 164 | 83.67 | 103,566 | 20.50 | 4.08 |
| 300–600 | 32 | 16.33 | 208,846 | 41.34 | 0.39 | |
| 600–900 | 0 | 0.00 | 133,188 | 26.36 | 0.00 | |
| 900–1000 | 0 | 0.00 | 17,855 | 3.53 | 0.00 | |
| 1000–2000 | 0 | 0.00 | 41,790 | 8.27 | 0.00 | |
| Aspect | Flat | 0 | 0.00 | 2749 | 0.54 | 0.00 |
| North | 34 | 17.35 | 77,236 | 15.29 | 1.13 | |
| Northeast | 25 | 12.76 | 64,499 | 12.77 | 1.00 | |
| East | 20 | 10.20 | 57,824 | 11.44 | 0.89 | |
| Southeast | 15 | 7.65 | 51,996 | 10.29 | 0.74 | |
| South | 27 | 13.78 | 62,269 | 12.32 | 1.12 | |
| Southwest | 18 | 9.18 | 54,352 | 10.76 | 0.85 | |
| West | 26 | 13.27 | 73,462 | 14.54 | 0.91 | |
| Northwest | 31 | 15.82 | 60,858 | 12.05 | 1.31 | |
| Catchment area (m2) | 900–9000 | 113 | 57.65 | 361,223 | 71.49 | 0.81 |
| 9000–25,000 | 75 | 38.27 | 120,329 | 23.82 | 1.61 | |
| >25,000 | 8 | 4.08 | 23,693 | 4.69 | 0.87 | |
| Catchment slope (°) | < 0.3 | 35 | 17.86 | 110,803 | 21.93 | 0.81 |
| 0.3–0.5 | 143 | 72.96 | 281,154 | 55.65 | 1.31 | |
| > 0.5 | 18 | 9.18 | 113,288 | 22.42 | 0.41 | |
| Curvature (°/100 m) | <–0.25 | 2 | 1.02 | 26,532 | 5.25 | 0.19 |
| -0.25–0.05 | 39 | 19.90 | 129,494 | 25.63 | 0.78 | |
| -0.05–0.15 | 132 | 67.35 | 280,986 | 55.61 | 1.21 | |
| >0.15 | 23 | 11.73 | 68,233 | 13.50 | 0.87 | |
| Magnitude (MS) | <1.4 | 97 | 49.49 | 211,196 | 41.80 | 1.18 |
| 1.4–1.7 | 76 | 38.78 | 195,731 | 38.74 | 1.00 | |
| >1.7 | 23 | 11.73 | 98,318 | 19.46 | 0.60 | |
| Distance to faults (m) | <1200 | 48 | 24.49 | 129,597 | 25.65 | 0.95 |
| 1200–2400 | 44 | 22.45 | 137,238 | 27.16 | 0.83 | |
| 2400–3600 | 42 | 21.43 | 113,788 | 22.52 | 0.95 | |
| 3600–5400 | 57 | 29.08 | 96,751 | 19.15 | 1.52 | |
| >5400 | 5 | 2.55 | 27,871 | 5.52 | 0.46 | |
| Land use | Residential | 43 | 21.94 | 26,063 | 5.16 | 4.25 |
| Forest | 5 | 2.55 | 70,400 | 13.93 | 0.18 | |
| Water | 29 | 14.80 | 86,629 | 17.15 | 0.86 | |
| Shrub | 11 | 5.61 | 106,239 | 21.03 | 0.27 | |
| Farmland | 108 | 55.10 | 215,914 | 42.73 | 1.29 | |
| Lithology | A | 4 | 2.04 | 36,276 | 7.18 | 0.28 |
| B | 8 | 4.08 | 83,547 | 16.54 | 0.25 | |
| C | 4 | 2.04 | 12,109 | 2.40 | 0.85 | |
| D | 10 | 5.10 | 68,380 | 13.53 | 0.38 | |
| E | 57 | 29.08 | 119,492 | 23.65 | 1.23 | |
| F | 57 | 29.08 | 78,188 | 15.48 | 1.88 | |
| G | 56 | 28.57 | 107,253 | 21.23 | 1.35 | |
| NDVI | <0.1 | 10 | 5.10 | 13,832 | 2.74 | 1.86 |
| 0.1–0.5 | 39 | 19.90 | 25,492 | 5.05 | 3.94 | |
| 0.5–0.7 | 76 | 38.78 | 112,911 | 22.35 | 1.74 | |
| >0.7 | 71 | 36.22 | 353,052 | 69.88 | 0.52 | |
| NDWI | <−0.6 | 99 | 50.51 | 413,436 | 81.83 | 0.62 |
| −0.6–−0.4 | 64 | 32.65 | 63,499 | 12.57 | 2.60 | |
| −0.4–0.3 | 26 | 13.27 | 18,352 | 3.63 | 3.65 | |
| >0.3 | 7 | 3.57 | 9998 | 1.98 | 1.80 | |
| Rainfall (mm/yr) | <980 | 83 | 42.35 | 243,656 | 48.23 | 0.88 |
| 980–1000 | 6 | 3.06 | 29,800 | 5.90 | 0.52 | |
| 1000–1030 | 47 | 23.98 | 160,937 | 31.85 | 0.75 | |
| 1030–1060 | 44 | 22.45 | 105,453 | 20.87 | 1.08 | |
| >1060 | 16 | 8.16 | 43,003 | 8.51 | 0.96 | |
| Distance to rivers (m) | <560 | 173 | 88.27 | 129,924 | 25.72 | 3.43 |
| 560–890 | 18 | 9.18 | 63,275 | 12.52 | 0.73 | |
| 890–1450 | 4 | 2.04 | 98,029 | 19.40 | 0.11 | |
| >1450 | 1 | 0.51 | 214,017 | 42.36 | 0.01 | |
| Slope (°) | <10 | 10 | 5.10 | 39,238 | 7.77 | 0.66 |
| 10–20 | 80 | 40.82 | 154,434 | 30.57 | 1.34 | |
| 20–30 | 74 | 37.76 | 173,889 | 34.42 | 1.10 | |
| 30–40 | 27 | 13.78 | 97,336 | 19.27 | 0.72 | |
| 40–50 | 5 | 2.55 | 31,630 | 6.26 | 0.41 | |
| 50–60 | 0 | 0.00 | 7419 | 1.47 | 0.00 | |
| >60 | 0 | 0.00 | 1299 | 0.26 | 0.00 | |
| Slope form | V/V | 67 | 34.18 | 144,923 | 28.68 | 1.19 |
| GE/V | 9 | 4.59 | 8311 | 1.64 | 2.79 | |
| X/V | 23 | 11.73 | 56,096 | 11.10 | 1.06 | |
| V/GR | 8 | 4.08 | 17,748 | 3.51 | 1.16 | |
| GE/GR | 1 | 0.51 | 3038 | 0.60 | 0.85 | |
| X/GR | 11 | 5.61 | 15,352 | 3.04 | 1.85 | |
| V/X | 23 | 11.73 | 69,636 | 13.78 | 0.85 | |
| GE/X | 5 | 2.55 | 12,208 | 2.42 | 1.06 | |
| X/X | 49 | 25.00 | 177,933 | 35.22 | 0.71 | |
| TPI | <−15 | 2 | 1.02 | 19,483 | 3.86 | 0.26 |
| −15–5 | 35 | 17.86 | 91,128 | 18.04 | 0.99 | |
| −5–2 | 99 | 50.51 | 186,356 | 36.88 | 1.37 | |
| 2–10 | 56 | 28.57 | 158,197 | 31.31 | 0.91 | |
| >10 | 4 | 2.04 | 50,081 | 9.91 | 0.21 | |
| TRI | <7 | 58 | 29.59 | 117,952 | 23.35 | 1.27 |
| 7–14 | 113 | 57.65 | 270,695 | 53.58 | 1.08 | |
| 14–21 | 21 | 10.71 | 88,865 | 17.59 | 0.61 | |
| 21–28 | 4 | 2.04 | 19,126 | 3.79 | 0.54 | |
| >28 | 0 | 0.00 | 8607 | 1.70 | 0.00 | |
| TSC | <42 | 20 | 10.20 | 22,695 | 4.49 | 2.27 |
| 42–49 | 82 | 41.84 | 133,494 | 26.42 | 1.58 | |
| 49–54 | 68 | 34.69 | 219,694 | 43.48 | 0.80 | |
| >54 | 26 | 13.27 | 129,362 | 25.60 | 0.52 | |
| TST | <23 | 68 | 34.69 | 80,958 | 16.02 | 2.17 |
| 23–29 | 81 | 41.33 | 171,818 | 34.01 | 1.22 | |
| 29–35 | 43 | 21.94 | 176,691 | 34.97 | 0.63 | |
| >35 | 4 | 2.04 | 75,778 | 15.00 | 0.14 | |
| TWI | <3 | 12 | 6.12 | 99,599 | 19.71 | 0.31 |
| 3–3.6 | 83 | 42.35 | 216,121 | 42.78 | 0.99 | |
| 3.6–4.2 | 86 | 43.88 | 147,164 | 29.13 | 1.51 | |
| 4.2–6.6 | 15 | 7.65 | 38,306 | 7.58 | 1.01 | |
| >6.6 | 0 | 0.00 | 4055 | 0.80 | 0.00 |
References
- Reichenbach, P.; Rossi, M.; Malamud, B.; Mihir, M.; Guzzetti, F. A Review of Statistically-Based Landslide Susceptibility Models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Zumpano, V.; Reichenbach, P.; Sterlacchini, S.; Micu, M.; van Westen, C.; Bălteanu, D. Different Landslide Sampling Strategies in a Grid-Based Bi-Variate Statistical Susceptibility Model. Geomorphology 2016, 253, 508–523. [Google Scholar] [CrossRef]
- Akgun, A.; Dag, S.; Bulut, F. Landslide Susceptibility Mapping for a Landslide-Prone Area (Findikli, Ne of Turkey) by Likelihood-Frequency Ratio and Weighted Linear Combination Models. Environ. Geol. 2008, 54, 1127–1143. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.T. Evaluation of a Combined Spatial Multi-Criteria Evaluation Model and Deterministic Model for Landslide Susceptibility Mapping. Catena 2016, 140, 125–139. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Nazmfar, H. Gis-Based Ordered Weighted Averaging and Dempster–Shafer Methods for Landslide Susceptibility Mapping in the Urmia Lake Basin, Iran. Int. J. Digit. Earth 2014, 7, 688–708. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.G.; Burlando, P. An Object-Oriented Computational Framework for the Simulation of Variably Saturated Flow in Soils, Using a Reduced Complexity Model. Environ. Model. Softw. 2012, 38, 191–202. [Google Scholar] [CrossRef]
- Van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial Data for Landslide Susceptibility, Hazard, and Vulnerability Assessment: An Overview. Eng. Geol. 2008, 102, 112–131. [Google Scholar] [CrossRef]
- Ilia, I.; Tsangaratos, P. Applying Weight of Evidence Method and Sensitivity Analysis to Produce a Landslide Susceptibility Map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
- Guri, P.K.; Patel, R.C. Spatial Prediction of Landslide Susceptibility in Parts of Garhwal Himalaya, India, Using the Weight of Evidence Modelling. Environ. Monit. Assess. 2015, 187, 324. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Liu, J.; Zhu, A.-X.; Chen, W. Application of Fuzzy Weight of Evidence and Data Mining Techniques in Construction of Flood Susceptibility Map of Poyang County, China. Sci. Total Environ. 2018, 625, 575–588. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Oreńczak, N.; Pasternak, M. Investigating the Effect of Cross-Modeling in Landslide Susceptibility Mapping. Appl. Sci. 2020, 10, 6335. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.-X. Exploring the Effects of the Design and Quantity of Absence Data on the Performance of Random Forest-Based Landslide Susceptibility Mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of Advanced Random Forest and Decision Tree Algorithms for Modeling Rainfall-Induced Landslide Susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef] [PubMed]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of Gis-Based Landslide Susceptibility Models Using Frequency Ratio, Logistic Regression, and Artificial Neural Network in a Tertiary Region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Zhao, Z. A Gis-Based Comparative Study of Dempster-Shafer, Logistic Regression and Artificial Neural Network Models for Landslide Susceptibility Mapping. Geocarto Int. 2017, 32, 367–385. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of Convolutional Neural Networks for Landslide Susceptibility Mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Integration of Convolutional Neural Network and Conventional Machine Learning Classifiers for Landslide Susceptibility Mapping. Comput. Geosci. 2020, 139, 104470. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on Landslide Susceptibility Mapping Using Support Vector Machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide Susceptibility Mapping & Prediction Using Support Vector Machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar]
- Bui, D.T.; Tuan, T.A.; Hoang, N.; Thanh, N.Q.; Nguyen, D.B.; van Liem, N.; Pradhan, B. Spatial Prediction of Rainfall-Induced Landslides for the Lao Cai Area (Vietnam) Using a Hybrid Intelligent Approach of Least Squares Support Vector Machines Inference Model and Artificial Bee Colony Optimization. Landslides 2017, 14, 447–458. [Google Scholar]
- Kittler, J. Multiple Classifier Systems. In Soft Computing Approach to Pattern Recognition and Image Processing; World Scientific: Singapore, 2002; pp. 3–22. [Google Scholar]
- Yan, F.; Zhang, Q.; Ye, S.; Ren, B. A Novel Hybrid Approach for Landslide Susceptibility Mapping Integrating Analytical Hierarchy Process and Normalized Frequency Ratio Methods with the Cloud Model. Geomorphology 2019, 327, 170–187. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An Ensemble Prediction of Flood Susceptibility Using Multivariate Discriminant Analysis, Classification and Regression Trees, and Support Vector Machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Termeh, S.; Vahid, R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood Susceptibility Mapping Using Novel Ensembles of Adaptive Neuro Fuzzy Inference System and Metaheuristic Algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M.B. Rotation Forest Fuzzy Rule-Based Classifier Ensemble for Spatial Prediction of Landslides Using Gis. Nat. Hazards 2016, 83, 97–127. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A Comparative Study of Heterogeneous Ensemble-Learning Techniques for Landslide Susceptibility Mapping. Int. J. Geogr. Inf. Sci. 2021, 35, 321–347. [Google Scholar] [CrossRef]
- Truong, X.; Mitamura, M.; Kono, Y.; Raghavan, V.; Yonezawa, G.; Do, T.; Bui, D.T.; Lee, S. Enhancing Prediction Performance of Landslide Susceptibility Model Using Hybrid Machine Learning Approach of Bagging Ensemble and Logistic Model Tree. Appl. Sci. 2018, 8, 1046. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Ho, T.; Pradhan, B.; Pham, B.; Nhu, V.; Revhaug, I. Gis-Based Modeling of Rainfall-Induced Landslides Using Data Mining-Based Functional Trees Classifier with Adaboost, Bagging, and Multiboost Ensemble Frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M.B. Hybrid Integration of Multilayer Perceptron Neural Networks and Machine Learning Ensembles for Landslide Susceptibility Assessment at Himalayan Area (India) Using Gis. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide Susceptibility Mapping Using J48 Decision Tree with Adaboost, Bagging and Rotation Forest Ensembles in the Guangchang Area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Kadavi, P.; Lee, C.-W.; Lee, S. Application of Ensemble-Based Machine Learning Models to Landslide Susceptibility Mapping. Remote Sens. 2018, 10, 1252. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance Evaluation of Gis-Based New Ensemble Data Mining Techniques of Adaptive Neuro-Fuzzy Inference System (Anfis) with Genetic Algorithm (Ga), Differential Evolution (De), and Particle Swarm Optimization (Pso) for Landslide Spatial Modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Bhargava, N.; Sharma, G.; Bhargava, R.; Mathuria, M. Decision Tree Analysis on J48 Algorithm for Data Mining. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 188–198. [Google Scholar]
- Bai, S.-B.; Jian, W.; Guo-Nian, L.; Ping-Gen, Z.; Sheng-Shan, H.; Su-Ning, X. Gis-Based and Data-Driven Bivariate Landslide-Susceptibility Mapping in the Three Gorges Area, China. Pedosphere 2009, 19, 14–20. [Google Scholar] [CrossRef]
- Peng, L.; Niu, R.; Huang, B.; Wu, X.; Zhao, Y.; Ye, R. Landslide Susceptibility Mapping Based on Rough Set Theory and Support Vector Machines: A Case of the Three Gorges Area, China. Geomorphology 2014, 204, 287–301. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide Susceptibility Modeling Applying Machine Learning Methods: A Case Study from Longju in the Three Gorges Reservoir Area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Kuncheva, I.L.; Rodríguez, J.J. An Experimental Study on Rotation Forest Ensembles. In Proceedings of the International Workshop on Multiple Classifier Systems, Prague, Czech Republic, 23–25 May 2007. [Google Scholar]
- Borrelli, L.; Ciurleo, M.; Gullà, G. Shallow Landslide Susceptibility Assessment in Granitic Rocks Using Gis-Based Statistical Methods: The Contribution of the Weathering Grade Map. Landslides 2018, 15, 1127–1142. [Google Scholar] [CrossRef]
- Pham, B.T.; Shirzadi, A.; Bui, D.T.; Prakash, I.; Dholakia, M.B. A Hybrid Machine Learning Ensemble Approach Based on a Radial Basis Function Neural Network and Rotation Forest for Landslide Susceptibility Modeling: A Case Study in the Himalayan Area, India. Int. J. Sediment Res. 2018, 33, 157–170. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B. Application of Time Series Analysis and Pso–Svm Model in Predicting the Bazimen Landslide in the Three Gorges Reservoir, China. Eng. Geol. 2016, 204, 108–120. [Google Scholar] [CrossRef]
- Tang, H.; Wasowski, J.; Juang, C.H. Geohazards in the Three Gorges Reservoir Area, China—Lessons Learned from Decades of Research. Eng. Geol. 2019, 261, 105267. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Niu, R.; Peng, L. Integration of Information Theory, K-Means Cluster Analysis and the Logistic Regression Model for Landslide Susceptibility Mapping in the Three Gorges Area, China. Remote Sens. 2017, 9, 938. [Google Scholar] [CrossRef] [Green Version]
- Tien, B.D.; Paraskevas, T.; Viet-Tien, N.; Van, L.N.; Trong, T.P. Comparing the Prediction Performance of a Deep Learning Neural Network Model with Conventional Machine Learning Models in Landslide Susceptibility Assessment. Catena 2020, 188, 104426. [Google Scholar]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide Susceptibility Modeling Using Reduced Error Pruning Trees and Different Ensemble Techniques: Hybrid Machine Learning Approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Pawłuszek, K.; Marczak, S.; Borkowski, A.; Tarolli, P. Multi-Aspect Analysis of Object-Oriented Landslide Detection Based on an Extended Set of Lidar-Derived Terrain Features. ISPRS Int. J. Geo Inform. 2019, 8, 321. [Google Scholar] [CrossRef] [Green Version]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide Susceptibility Mapping Using Random Forest, Boosted Regression Tree, Classification and Regression Tree, and General Linear Models and Comparison of Their Performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Iwahashi, J.; Pike, R.J. Automated Classifications of Topography from Dems by an Unsupervised Nested-Means Algorithm and a Three-Part Geometric Signature. Geomorphology 2007, 86, 409–440. [Google Scholar] [CrossRef]
- Sörensen, R.; Zinko, U.; Seibert, J. On the Calculation of the Topographic Wetness Index: Evaluation of Different Methods Based on Field Observations. Hydrol. Earth Syst. Sci. Discuss. 2006, 10, 101–112. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Wang, Y.; Niu, R.; Hu, Y. A Combination of Geographically Weighted Regression, Particle Swarm Optimization and Support Vector Machine for Landslide Susceptibility Mapping: A Case Study at Wanzhou in the Three Gorges Area, China. Int. J. Environ. Res. Public Health 2016, 13, 487. [Google Scholar] [CrossRef] [Green Version]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A Deep Learning Algorithm Using a Fully Connected Sparse Autoencoder Neural Network for Landslide Susceptibility Prediction. Landslides 2019, 17, 1–13. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H. Feature Selection for Classification. Intell. Data Anal. 1997, 1, 131–156. [Google Scholar] [CrossRef]
- Micheletti, N.; Foresti, L.; Robert, S.; Leuenberger, M.; Pedrazzini, A.; Jaboyedoff, M.; Kanevski, M. Machine Learning Feature Selection Methods for Landslide Susceptibility Mapping. Math. Geosci. 2014, 46, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Mason, L. The Alternating Decision Tree Learning Algorithm. In Proceedings of the 16th International Conference on Machine Learning ICML, Bled, Slovenia, 27–30 June 1999. [Google Scholar]
- Adnan, M.N.; Islam, M.Z. Forest Pa: Constructing a Decision Forest by Penalizing Attributes Used in Previous Trees. Expert Syst. Appl. 2017, 89, 389–403. [Google Scholar] [CrossRef]
- Gama, J. Functional Trees. Mach. Learn. 2004, 55, 219–250. [Google Scholar] [CrossRef]
- Landwehr, N.; Hall, M.; Frank, E. Logistic Model Trees. Mach. Learn. 2005, 59, 161–205. [Google Scholar] [CrossRef] [Green Version]
- Hulten, G.; Spencer, L.; Domingos, P. Mining Time-Changing Data Streams. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 26–29 August 2001. [Google Scholar]
- Nguyen, Q.-K.; Bui, D.T.; Hoang, N.; Trinh, P.T.; Nguyen, V.; Yilmaz, I. A Novel Hybrid Approach Based on Instance Based Learning Classifier and Rotation Forest Ensemble for Spatial Prediction of Rainfall-Induced Shallow Landslides Using Gis. Sustainability 2017, 9, 813. [Google Scholar] [CrossRef] [Green Version]
- Youssef, A.M.; Pourghasemi, H.R.; El-Haddad, B.A.; Dhahry, B.K. Landslide Susceptibility Maps Using Different Probabilistic and Bivariate Statistical Models and Comparison of Their Performance at Wadi Itwad Basin, Asir Region, Saudi Arabia. Bull. Eng. Geol. Environ. 2016, 75, 63–87. [Google Scholar] [CrossRef]
- Sandric, I.; Ionita, C.; Chitu, Z.; Dardala, M.; Irimia, R.; Furtuna, F.T. Using Cuda to Accelerate Uncertainty Propagation Modelling for Landslide Susceptibility Assessment. Environ. Model. Softw. 2019, 115, 176–186. [Google Scholar] [CrossRef]
- Basu, T.; Pal, S. Rs-Gis Based Morphometrical and Geological Multi-Criteria Approach to the Landslide Susceptibility Mapping in Gish River Basin, West Bengal, India. Adv. Space Res. 2018, 63, 1253–1269. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I. Machine Learning Methods of Kernel Logistic Regression and Classification and Regression Trees for Landslide Susceptibility Assessment at Part of Himalayan Area, India. Indian J. Sci. Technol. 2018, 11, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.; Mandal, K. Modeling and Mapping Landslide Susceptibility Zones Using Gis Based Multivariate Binary Logistic Regression (Lr) Model in the Rorachu River Basin of Eastern Sikkim Himalaya, India. Model. Earth Syst. Environ. 2018, 4, 69–88. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative Study of Landslide Susceptibility Mapping with Different Recurrent Neural Networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Jebur, M.N.; Bui, D.T.; Xu, C.; Akgun, A. Spatial Prediction of Landslide Hazard at the Luxi Area (China) Using Support Vector Machines. Environ. Earth Sci. 2016, 75, 40. [Google Scholar] [CrossRef]
- Lombardo, L.; Mai, P.M. Presenting logistic regression-based landslide susceptibility results. Eng. Geol. 2018, 244, 14–24. [Google Scholar] [CrossRef]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Pham, B.T.; Pradhan, B. Novel Gis Based Machine Learning Algorithms for Shallow Landslide Susceptibility Mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, B. Application of an Advanced Fuzzy Logic Model for Landslide Susceptibility Analysis. Int. J. Comput. Intel. Syst. 2010, 3, 370–381. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Bui, D.T. Landslide Susceptibility Evaluation and Management Using Different Machine Learning Methods in the Gallicash River Watershed, Iran. Remote Sens. 2020, 12, 475. [Google Scholar] [CrossRef] [Green Version]
- Crozier, M.J. A Proposed Cell Model for Multiple-Occurrence Regional Landslide Events: Implications for Landslide Susceptibility Mapping. Geomorphology 2017, 295, 480–488. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. A Comparative Study of Landslide Susceptibility Maps Produced Using Support Vector Machine with Different Kernel Functions and Entropy Data Mining Models in China. Bull. Eng. Geol. Environ. 2018, 77, 647–664. [Google Scholar] [CrossRef]
- Soma, A.S.; Kubota, T.; Mizuno, H. Optimization of Causative Factors Using Logistic Regression and Artificial Neural Network Models for Landslide Susceptibility Assessment in Ujung Loe Watershed, South Sulawesi Indonesia. J. Mountain Sci. 2019, 16, 383–401. [Google Scholar] [CrossRef]
- Bai, S.-B.; Wang, J.; Lü, G.; Zhou, P.; Hou, S.; Xu, S. Gis-Based Logistic Regression for Landslide Susceptibility Mapping of the Zhongxian Segment in the Three Gorges Area, China. Geomorphology 2010, 115, 23–31. [Google Scholar] [CrossRef]
- Büechi, B.; Jan, K.; Holger, F.; Christain, H.; Tazio, S.; Alejo, C. Regional-Scale Landslide Susceptibility Modelling in the Cordillera Blanca, Peru—A Comparison of Different Approaches. Landslides 2019, 16, 395–407. [Google Scholar] [CrossRef]









| Factors | Implementation/Calculation | Sources |
|---|---|---|
| Altitude | Extracted from DEM data using the ArcGIS software [35,42,46]. | ASTER GDEM Version 2 |
| Aspect | ||
| Curvature | ||
| Slope | ||
| Catchment area | ||
| Catchment slope | ||
| Slope form | ||
| TPI | Extracted form DEM data using the SAGA software [42,47,48]. | |
| TRI | ||
| TSC | ||
| TST | ||
| TWI | ||
| Distance to rivers | Extracting the main river lines and using the Euclidean Distance tool in ArcGIS software to calculate distance to rivers. | |
| Lithology | Extracted from a 1: 50,000 geological map. | Hubei Geological Bureau (http://dzj.hubei.gov.cn) |
| Distance to faults | Extracting the fault lines form the geological map and used the Euclidean Distance tool in ArcGIS software to calculate distance to faults. | |
| Land use | Using a support vector machine method to classify the images into five land use classes with an overall accuracy of 93.95%. | Landsat 7 ETM + images |
| NDVI | Calculated from remote sensing images using the ENVI software [49,50]. | |
| NDWI | ||
| Magnitude | Using a Kriging interpolation method to generate magnitude raster data. | Historical earthquakes and instruments monitored data since 1970 |
| Rainfall | Using an inverse distance weighted spatial interpolation method to generate the rainfall factor. | 6 rainfall stations |
| Methods | Parameters | ||
|---|---|---|---|
| Base classifiers | ADT | Batch size: 100; number of boosting iterations: 10; seed: 1. | |
| FPA | Batch size: 100; number of trees: 15; number of pruning folds: 2; seed: 1. | ||
| FT | Batch size: 100; number of boosting iterations: 15; minimum number of instances: 15. | ||
| LMT | Batch size: 100; number of boosting iterations: 15; minimum number of instances: 15 | ||
| VFDT | Batch size: 100; grace period: 200; hoeffding tie threshold: 0.05; minimum fraction of weight info gain: 0.01. | ||
| Ensembles | ADT+RF | Base classifier: ADT; number of iterations: 26. | Minimum size of the group: 3; maximum size of the group: 3; removed percentage of in-stance: 50; principal components analysis used for projection filter; number of iterations: 26; seed: 1. |
| FPA+RF | Base classifier: FPA; number of iterations: 11. | ||
| FT+RF | Base classifier: FT; number of iterations: 20. | ||
| LMT+RF | Base classifier: LMT; number of iterations: 26. | ||
| VFDT+RF | Base classifier: VFDT; number of iterations: 10. | ||
| Classes | Landslide Density | ||||
|---|---|---|---|---|---|
| ADT | FPA | FT | LMT | VFDT | |
| Very low | 0.02 | 0.03 | 0.10 | 0.02 | 0.02 |
| Low | 0.09 | 0.59 | 0.33 | 0.43 | 0.10 |
| Moderate | 0.98 | 0.73 | 0.51 | 0.77 | 0.50 |
| High | 1.28 | 2.59 | 2.04 | 1.74 | 0.61 |
| Very high | 4.12 | 5.22 | 4.07 | 4.96 | 4.18 |
| ADT+RF | FPA+RF | FT+RF | LMT+RF | VFDT+RF | |
| Very low | 0.00 | 0.01 | 0.02 | 0.00 | 0.04 |
| Low | 0.19 | 0.65 | 0.11 | 0.34 | 0.56 |
| Moderate | 0.52 | 0.52 | 0.52 | 0.79 | 1.31 |
| High | 1.34 | 1.42 | 1.65 | 1.30 | 1.34 |
| Very high | 5.85 | 5.49 | 6.04 | 5.78 | 4.94 |
| Methods | OA Value | MCC |
|---|---|---|
| ADT | 77.97% | 0.561 |
| ADT+RF | 80.51% | 0.610 |
| FPA | 76.27% | 0.526 |
| FPA+RF | 77.12% | 0.543 |
| FT | 75.42% | 0.509 |
| FT+RF | 83.05% | 0.661 |
| LMT | 79.66% | 0.594 |
| LMT+RF | 81.36% | 0.629 |
| VFDT | 79.66% | 0.596 |
| VFDT+RF | 80.53% | 0.615 |
| Comparative Pairs | Chi–Square Value | p Value | Significance Level |
|---|---|---|---|
| ADT vs. ADT+RF | 813.288 | <0.0001 | Yes |
| FPA vs. FPA+RF | 854.927 | <0.0001 | Yes |
| FT vs. FT+RF | 634.815 | <0.0001 | Yes |
| LMT vs. LMT+RF | 824.088 | <0.0001 | Yes |
| VFDY vs. VFDT+RF | 612.270 | <0.0001 | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Wang, Y.; Duan, G.; Peng, L. Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sens. 2021, 13, 238. https://doi.org/10.3390/rs13020238
Fang Z, Wang Y, Duan G, Peng L. Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sensing. 2021; 13(2):238. https://doi.org/10.3390/rs13020238
Chicago/Turabian StyleFang, Zhice, Yi Wang, Gonghao Duan, and Ling Peng. 2021. "Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China" Remote Sensing 13, no. 2: 238. https://doi.org/10.3390/rs13020238
APA StyleFang, Z., Wang, Y., Duan, G., & Peng, L. (2021). Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sensing, 13(2), 238. https://doi.org/10.3390/rs13020238