High-Resolution SAR Image Classification Using Multi-Scale Deep Feature Fusion and Covariance Pooling Manifold Network
Abstract
:1. Introduction
- Intricate spatial structural patterns: Due to the coherent imaging mechanism and object shadow occlusion, pixels of the same object will present a high degree of variability, known as speckle [3]. Moreover, HR SAR images contain more strong scattering points, and the arrangements of numerous and various objects have become more complicated. In this context, HR SAR images will have a great intra-class variation and little inter-class difference between objects [4]. As shown in Figure 1a,b, we have given two low-density residential areas from the same category and two different categories including open land and water areas. Therefore, extracting more discriminative and precise spatial features for HR SAR image classification is still a highly challenging task.
- Complex statistical nature: The unique statistical characteristics of SAR data are also crucial for SAR image modeling and classification. In HR SAR images, the number of elementary scatterers present in a single-resolution cell is reduced. Traditional statistical models for low- and medium-resolution SAR, such as Gamma [5], K [6], Log-normal [7], etc., find it difficult to provide a good approximation for the distribution of HR SAR data. Meanwhile, accurate modeling of HR SAR data using statistical models may require designing and solving more complex parameter estimation equations. Hence, it is also a challenge to effectively capture the statistical properties contained in the SAR image to enhance the discrimination of land-cover representations.
1.1. Related Work
1.2. Motivations and Contributions
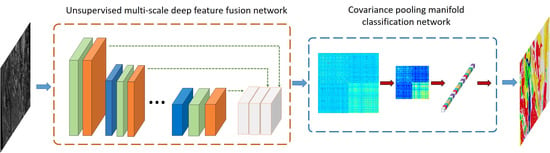
- We propose a Gabor-filtering-based multi-scale feature fusion network (MFFN) to obtain the effective spatial feature representation. MFFN combines the strengths of unsupervised denoising dual-sparse encoder and multi-scale CNN to learn discriminative features of HR SAR images. Meanwhile, MFFN introduces the feature fusion strategies in both intra-layer and inter-layer to adequately utilize the complementary information between different layers and different scales.
- We introduce a covariance pooling manifold network (CPMN) to capture the statistical properties of the HR SAR image in the MFFN feature space. The CPMN characterizes the distributions of spatial features by covariance-based second-order statistics and incorporates the covariance matrix into the deep network architecture to further make the global covariance statistical descriptor more discriminative of various land covers.
2. Materials and Methods
2.1. Gabor Filtering-Based Multi-Scale Deep Fusion Feature Extraction
2.1.1. Extraction of Gabor Features
2.1.2. Multi-Scale Deep Feature Fusion Network
2.1.3. Greedy Layer-Wise Unsupervised Feature Learning
| Algorithm 1 Gabor filtering-based multiscale unsupervised deep fusion feature extraction. |
| Input: The SAR image , Layer number |
| 1: Extract Gabor features of the SAR image based on (1). |
| 2: Initialize input feature maps ; |
| 3: Initialize weights and bias ; |
| 4: for to do |
| 5: Generate by randomly extracting patches from ; Corrupt |
| into , and map to by (7) and (8); |
| 6: Obtain , by solving (9) and update the parameters of MFFN; |
| 7: Extract layer multiscale feature of MFFN by (2), and get the final feature output |
| by sum fusion: ; |
| 8: end for |
| Output: The pretrained MFFN model. |
2.2. Global Second-Order Statistics Extraction and Classification Based on CPMN
2.2.1. Multilayer Feature Fusion Based on Covariance Pooling
2.2.2. Covariance Features Classification Based on Manifold Network
| Algorithm 2 Manifold Network Training. |
| Input: Training samples , and corresponding labels , number |
| of BP epochs R. |
| 1: compute covariance matrix of each using (10) and (11); |
| 2: Initialize weights of each BiMap layers, rectification ; |
| 3: while epoch to do |
| 4: while training sample to do |
| Compute the matrix mapping by (12), (13) and (14); |
| Compute the softmax activation and the loss function by (15); |
| 5: Back-propagate error to compute cross-entropy loss gradient ; |
| 6: The loss of the k-th layer could be denoted by a function as |
| 7: Update network parameter of each layer based on partial derivatives |
| , |
| 8: The update formula for the BiMap layer parameter is |
| where , ; |
| 9: The gradients of the involved data in the layers below can be compute |
| For the ReEig layers |
| , |
| For the LogEig layer |
| , |
| 10: end while |
| 11: end while |
| Output: The trained Manifold network classification model. |
3. Results
3.1. Experimental Data and Settings
3.2. Parameter Settings and Performance Analysis of the Proposed MFFN-CPMN model
3.2.1. Effect of the Feature Number
3.2.2. Effect of Multi-Scale Convolution Kernel
3.2.3. Effect of the Denoising Dual-Sparse Encoder and Depth
3.2.4. Effect of Multi-Layer Feature Fusion
3.2.5. Effect of Covariance Pooling Manifold Network
3.3. Experiments Results and Comparisons
3.3.1. TerraSAR-X SAR Image
3.3.2. Gaofen-3 SAR Image
3.3.3. Airborne SAR Image
3.3.4. F-SAR Image
3.4. Discussion on Transferability of Pre-Trained MFFN
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; Zan, F.D.; Bräutigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the processing of very high resolution spaceborne SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar] [CrossRef] [Green Version]
- Deledalle, C.A.; Denis, L.; Tabti, S.; Tupin, F. MuLoG, or How to apply Gaussian denoisers to multi-channel SAR speckle reduction? IEEE Trans. Image Process. 2017, 26, 4389–4403. [Google Scholar] [CrossRef] [Green Version]
- Dumitru, C.O.; Datcu, M. Information content of very high resolution SAR images: Study of feature extraction and imaging parameters. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4591–4610. [Google Scholar] [CrossRef]
- Martín-de-Nicolás, J.; Jarabo-Amores, M.-P.; Mata-Moya, D.; del-Rey-Maestre, N.; Bárcena-Humanes, J.-L. Statistical analysis of SAR sea clutter for classification purposes. Remote Sens. 2014, 6, 9379–9411. [Google Scholar]
- Joughin, I.R.; Percival, D.B.; Winebrenner, D.P. Maximum likelihood estimation of K distribution parameters for SAR data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 989–999. [Google Scholar] [CrossRef]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Academic: San Diego, CA, USA, 1990; Chapter 3. [Google Scholar]
- Dai, D.; Yang, W.; Sun, H. Multilevel local pattern histogram for SAR image classification. IEEE Geosci. Remote Sens. Lett. 2011, 8, 225–229. [Google Scholar] [CrossRef]
- Cui, S.; Dumitru, C.O.; Datcu, M. Ratio-detector-based feature extraction for very high resolution SAR image patch indexing. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1175–1179. [Google Scholar]
- Popescu, A.; Gavat, I.; Datcu, M. Contextual descriptors for scene classes in very high resolution SAR images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 80–84. [Google Scholar] [CrossRef]
- Dumitru, C.O.; Schwarz, G.; Datcu, M. Land cover semantic annotation derived from high-resolution SAR images. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2016, 9, 2215–2232. [Google Scholar] [CrossRef] [Green Version]
- Soh, L.-K.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. IEEE Trans. Geosci. Remote Sens. 1999, 37, 780–795. [Google Scholar] [CrossRef] [Green Version]
- Tombak, A.; Turkmenli, I.; Aptoula, E.; Kayabol, K. Pixel-based classification of SAR images using feature attribute profiles. IEEE Geosci. Remote Sens. Lett. 2019, 16, 564–567. [Google Scholar] [CrossRef]
- Song, S.; Xu, B.; Yang, J. SAR target recognition via supervised discriminative dictionary learning and sparse representation of the SARHOG feature. Remote Sens. 2016, 8, 683. [Google Scholar] [CrossRef] [Green Version]
- Guan, D.; Xiang, D.; Tang, X.; Wang, L.; Kuang, G. Covariance of Textural Features: A New Feature Descriptor for SAR Image Classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 3932–3942. [Google Scholar] [CrossRef]
- Bridle, J.S. Training stochastic model recognition algorithms as networks can lead to maximum mutual information estimation of parameters. In Advances in Neural Information Processing Systems; Morgan Kaufmann: San Mateo, CA, USA, 1990; pp. 211–217. [Google Scholar]
- Maulik, U.; Chakraborty, D. Remote Sensing Image Classification: A survey of support-vector-machine-based advanced techniques. IEEE Geosci. Remote Sens. Mag. 2017, 5, 33–52. [Google Scholar] [CrossRef]
- Tison, C.; Nicolas, J.M.; Tupin, F.; Maitre, H. A new statistical model for Markovian classification of urban areas in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2046–2057. [Google Scholar] [CrossRef]
- Li, H.C.; Hong, W.; Wu, Y.R.; Fan, P.Z. On the empirical-statistical modeling of SAR images with generalized gamma distribution. IEEE J. Sel. Top. Signal Process. 2011, 5, 386–397. [Google Scholar]
- Goodman, J.W. Statistical properties of laser speckle patterns. In Laser Speckle and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 1975; pp. 9–75. [Google Scholar]
- Kuruoglu, E.E.; Zerubia, J. Modeling SAR images with a generalization of the Rayleigh distribution. IEEE Trans. Image Process. 2004, 13, 527–533. [Google Scholar] [CrossRef]
- Doulgeris, A.P.; Anfinsen, S.N.; Eltoft, T. Classification with a Non-Gaussian Model for PolSAR Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2999–3009. [Google Scholar] [CrossRef] [Green Version]
- Li, H.C.; Krylov, V.A.; Fan, P.Z.; Zerubia, J.; Emery, W.J. Unsupervised learning of generalized gamma mixture model with application in statistical modeling of high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2153–2170. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Peng, R.; Wang, C. A two-component k–lognormal mixture model and its parameter estimation method. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2640–2651. [Google Scholar] [CrossRef]
- Cintra, R.J.; Rgo, L.C.; Cordeiro, G.M.; Nascimento, A.D.C. Beta generalized normal distribution with an application for SAR image processing. Statistics 2014, 48, 279–294. [Google Scholar] [CrossRef]
- Wu, W.; Guo, H.; Li, X.; Ferro-Famil, L.; Zhang, L. Urban land use information extraction using the ultrahigh-resolution Chinese Airborne SAR imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5583–5599. [Google Scholar]
- Yue, D.X.; Xu, F.; Frery, A.C. A Generalized Gaussian Coherent Scatterer Model for Correlated SAR Texture. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2947–2964. [Google Scholar] [CrossRef]
- Voisin, A.; Krylov, V.A.; Moser, G.; Serpico, S.B.; Zerubia, J. Classification of very high resolution SAR images of urban areas using copulas and texture in a hierarchical Markov random field model. IEEE Geosci. Remote Sens. Lett. 2013, 10, 96–100. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Geng, J.; Fan, J.; Wang, H.; Ma, X.; Li, B.; Chen, F. High–resolution SAR image classification via deep convolutional autoencoders. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2351–2355. [Google Scholar] [CrossRef]
- Geng, J.; Wang, H.; Fan, J.; Ma, X. Deep supervised and contractive neural network for SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2442–2459. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, L.; Zhao, J.; Gu, J.; Zhao, J. Discriminant deep belief network for high-resolution SAR image classification. Pattern Recognit. 2017, 61, 686–701. [Google Scholar] [CrossRef]
- Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional neural network with data augmentation for SAR target recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y.Q. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Li, J.; Wang, C.; Wang, S.; Zhang, H.; Zhang, B. Classification of very high resolution SAR image based on convolutional neural network. In Proceedings of the International Workshop on Remote Sensing with Intelligent Processing, Shanghai, China, 18–21 May 2017. [Google Scholar]
- Geng, J.; Deng, X.; Ma, X.; Jiang, W. Transfer Learning for SAR Image Classification via Deep Joint Distribution Adaptation Networks. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5377–5392. [Google Scholar] [CrossRef]
- Wu, W.; Li, H.; Li, X.; Guo, H.; Zhang, L. Polsar image semantic segmentation based on deep transfer learning-realizing smooth classification with small training sets. IEEE Geosci. Remote Sens. Lett. 2019, 16, 977–981. [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, M.; Cao, Z.; Cao, C. Image data augmentation for SAR sensor via generative adversarial nets. IEEE Access 2019, 7, 42255–42268. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Wang, K.; Leung, H. SAR Target Recognition Based on Variational Autoencoder. In Proceedings of the IEEE MTT-S International Microwave Biomedical Conference (IMBioC), Nanjing, China, 6–8 May 2019; Volume 1. [Google Scholar]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised deep feature extraction for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; He, C.; Zhang, Q.; Liao, M. Statistical Convolutional Neural Network for Land-Cover Classification from SAR Images. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1548–1552. [Google Scholar] [CrossRef]
- Tuzel, O.; Porikli, F.; Meer, P. Region covariance: A fast descriptor for detection and classification. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; Volume 2, pp. 589–600. [Google Scholar]
- He, N.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Remote sensing scene classification using multi-layer stacked covariance pooling. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6899–6910. [Google Scholar] [CrossRef]
- Li, X.; Lei, L.; Sun, Y.; Li, M.; Kuang, G. Multimodal Bilinear Fusion Network with Second-Order Attention-Based Channel Selection for Land Cover Classification. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2020, 13, 1011–1026. [Google Scholar] [CrossRef]
- Arsigny, V.; Fillard, P.; Pennec, X.; Ayache, N. Geometric means in a novel vector space structure on symmetric positive-definite matrices. SIAM J. Matrix Anal. Appl. 2007, 29, 328–347. [Google Scholar] [CrossRef] [Green Version]
- Grigorescu, S.E.; Petkov, N.; Kruizinga, P. Comparison of texture features based on gabor filters. IEEE Trans. Image Process. 2002, 11, 1160–1167. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Wechsler, H. Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition. IEEE Trans. Image Process. 2002, 11, 467–476. [Google Scholar] [PubMed] [Green Version]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Coates, A.; Ng, A.Y.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 11–13 April 2011; pp. 215–223. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM: New York, NY, USA, 2008; pp. 1096–1103. [Google Scholar]
- Zeiler, M.D. ADADELTA: An adaptive learning rate method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in network. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014; pp. 1–10. [Google Scholar]
- Wang, W.; Wang, R.; Huang, Z.; Shan, S.; Chen, X. Discriminant analysis on Riemannian manifold of Gaussian distributions for face recognition with image sets. IEEE Trans. Image Process. 2018, 27, 151–163. [Google Scholar] [CrossRef]
- Huang, Z.; Van Gool, L. A Riemannian network for spd matrix learning. In Proceedings of the Association for the Advance Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Abeyruwan, S.W.; Sarkar, D.; Sikder, F.; Visser, U. Semi-automatic extraction of training examples from sensor readings for fall detection and posture monitoring. IEEE Sens. J. 2016, 16, 5406–5415. [Google Scholar] [CrossRef]

















| Satellite | Band | Size | Resolution | Polarization | Date | Location |
|---|---|---|---|---|---|---|
| TerraSAR-X | X | 1450*2760 | 0.5 m | HH | 10/2013 | Lillestroem, Norway |
| Chinese Gaofen-3 | C | 2600*4500 | 1 m | HH | 03/2017 | Guangdong, China |
| Chinese Airborne | Ku | 1800*3000 | 0.3 m | HH | 10/2016 | Shaanxi, China |
| F-SAR | X | 6187*4278 | 0.67 m | VV | 10/2007 | Traunstein, Germany |
| Accuracy | One Layer | Two Layers | Three Layers | Four Layers | |
|---|---|---|---|---|---|
| With Denosing | OA | 0.8064 | 0.8351 | 0.8578 | 0.8673 |
| AA | 0.8004 | 0.8305 | 0.8559 | 0.8711 | |
| Kappa | 0.7352 | 0.7730 | 0.8031 | 0.8162 | |
| Without Denosing | OA | 0.7960 | 0.8254 | 0.8403 | 0.8490 |
| AA | 0.7839 | 0.8215 | 0.8414 | 0.8514 | |
| Kappa | 0.7211 | 0.7603 | 0.7801 | 0.7916 |
| Fusing Methods | Model Size | Training Time | OA | AA |
|---|---|---|---|---|
| Intra-sum&inter-none | 41M | 3072 s | 0.8383 | 0.8449 |
| Intra-sum&inter-sum | 41M | 3149 s | 0.8170 | 0.8101 |
| Intra-sum&inter-concat | 41M | 3153 s | 0.8673 | 0.8711 |
| Intra-concat &inter-none | 117M | 7886 s | 0.8592 | 0.8635 |
| Intra-concat &inter-sum | 117M | 7934 s | 0.8486 | 0.8475 |
| Intra-concat &inter-concat | 117M | 8087 s | 0.8763 | 0.8800 |
| Model | Method | OA | AA | Kappa |
|---|---|---|---|---|
| M-1 | LFFN + GAP | 0.8488 | 0.8499 | 0.7910 |
| M-2 | LFFN + CPMN (200) | 0.8648 | 0.8767 | 0.8182 |
| M-3 | LFFN + CPMN (200–100) | 0.8653 | 0.8764 | 0.8134 |
| M-4 | LFFN + CPMN (200–100–50) | 0.8499 | 0.8594 | 0.7925 |
| M-5 | MFFN + GAP | 0.8673 | 0.8711 | 0.8162 |
| M-6 | MFFN + CPMN (800) | 0.8923 | 0.8975 | 0.8499 |
| M-7 | MFFN + CPMN (800–400) | 0.8933 | 0.8978 | 0.8511 |
| M-8 | MFFN + CPMN (800–400–200) | 0.8903 | 0.8952 | 0.8471 |
| M-9 | MFFN + CPMN (800–400–200–100) | 0.8835 | 0.8893 | 0.8378 |
| Gabor | CoTF | BOVW | DCAE | EPLS | SCNN | A-ConvNet | MFFN-GAP | MSCP | MFFN-CPMN | |
|---|---|---|---|---|---|---|---|---|---|---|
| Water | 93.68 ± 1.04 | 91.89 ± 0.16 | 84.27 ± 0.16 | 92.16 ± 0.73 | 90.02 ± 0.77 | 96.39 ± 0.87 | 93.83 ± 0.50 | 95.81 ± 1.08 | 97.85 ± 0.80 | 97.73 ± 0.31 |
| Residential | 86.03 ± 0.66 | 87.12 ± 1.67 | 81.50 ± 1.51 | 80.09 ± 0.88 | 77.50 ± 1.55 | 88.82 ± 0.13 | 85.57 ± 1.59 | 87.02 ± 1.02 | 91.19 ± 1.02 | 91.43 ± 0.92 |
| Wood land | 71.94 ± 0.57 | 82.77 ± 1.78 | 77.84 ± 1.22 | 77.44 ± 0.79 | 71.13 ± 0.03 | 85.44 ± 0.38 | 94.38 ± 1.43 | 88.06 ± 0.67 | 91.17 ± 0.67 | 92.13 ± 0.25 |
| Open land | 54.88 ± 1.03 | 70.89 ± 1.56 | 69.97 ± 1.10 | 74.48 ± 1.38 | 70.02 ± 0.85 | 80.40 ± 0.74 | 76.65 ± 0.63 | 86.09 ± 0.85 | 84.46 ± 0.85 | 85.89 ± 0.32 |
| Road | 28.54 ± 1.67 | 48.19 ± 0.62 | 69.79 ± 0.12 | 67.91 ± 0.42 | 59.81 ± 0.32 | 67.98 ± 0.83 | 81.24 ± 0.11 | 78.55 ± 0.29 | 81.48 ± 0.29 | 81.72 ± 1.08 |
| OA | 69.96 ± 0.64 | 78.60 ± 0.03 | 76.44 ± 0.06 | 77.60 ± 0.88 | 73.49 ± 0.05 | 84.46 ± 0.39 | 84.00 ± 0.34 | 86.73 ± 0.08 | 88.69 ± 0.08 | 89.33 ± 0.18 |
| AA | 67.01 ± 0.32 | 76.17 ± 0.13 | 76.68 ± 0.11 | 78.41 ± 0.67 | 73.70 ± 0.15 | 83.81 ± 0.29 | 86.34 ± 0.23 | 87.11 ± 0.35 | 89.35 ± 0.35 | 89.78 ± 0.38 |
| 59.49 ± 0.63 | 70.65 ± 0.03 | 67.94 ± 0.04 | 69.56 ± 1.11 | 64.30 ± 0.07 | 78.42 ± 0.49 | 78.14 ± 0.37 | 81.62 ± 0.15 | 84.26 ± 0.15 | 85.11 ± 0.27 |
| Gabor | CoTF | BOVW | DCAE | EPLS | SCNN | A-ConvNet | MFFN-GAP | MSCP | MFFN-CPMN | |
|---|---|---|---|---|---|---|---|---|---|---|
| Mountain | 46.23 ± 0.51 | 71.57 ± 0.54 | 51.57 ± 1.16 | 61.85 ± 0.80 | 49.28 ± 0.29 | 81.75 ± 0.90 | 85.24 ± 0.36 | 83.18 ± 0.09 | 81.25 ± 0.74 | 84.04 ± 0.36 |
| Water | 92.85 ± 0.24 | 89.05 ± 0.08 | 91.03 ± 0.09 | 91.28 ± 0.14 | 93.45 ± 0.28 | 94.56 ± 1.15 | 95.54 ± 0.86 | 96.02 ± 0.28 | 95.16 ± 0.34 | 95.42 ± 0.12 |
| Building | 58.04 ± 1.25 | 82.06 ± 1.01 | 67.91 ± 0.37 | 77.46 ± 0.66 | 60.71 ± 0.03 | 81.16 ± 1.09 | 86.67 ± 1.30 | 84.44 ± 0.13 | 86.89 ± 0.46 | 89.89 ± 0.05 |
| Roads | 69.25 ± 0.04 | 91.24 ± 0.18 | 87.14 ± 0.80 | 93.57 ± 1.06 | 68.98 ± 3.15 | 92.78 ± 0.08 | 92.90 ± 0.77 | 95.46 ± 0.33 | 97.70 ± 0.17 | 98.38 ± 0.88 |
| Woodland | 81.24 ± 1.67 | 84.30 ± 0.46 | 80.26 ± 1.00 | 84.83 ± 0.30 | 78.45 ± 0.83 | 84.33 ± 0.42 | 66.49 ± 0.11 | 87.30 ± 0.39 | 88.24 ± 0.64 | 89.45 ± 0.07 |
| Open land | 69.48 ± 0.75 | 69.60 ± 0.47 | 72.43 ± 0.80 | 74.32 ± 1.11 | 55.48 ± 0.79 | 78.49 ± 0.92 | 95.91 ± 0.32 | 89.22 ± 0.66 | 92.93 ± 0.77 | 94.31 ± 0.78 |
| OA | 67.18 ± 0.16 | 80.58 ± 0.52 | 71.32 ± 0.61 | 77.60 ± 0.59 | 67.70 ± 0.08 | 84.94 ± 0.41 | 86.76 ± 0.27 | 87.72 ± 0.06 | 88.10 ± 0.28 | 90.03 ± 0.17 |
| AA | 69.52 ± 0.59 | 81.30 ± 0.12 | 75.09 ± 0.86 | 80.55 ± 0.37 | 67.73 ± 0.38 | 85.51 ± 0.27 | 87.12 ± 0.57 | 89.27 ± 0.05 | 90.36 ± 0.09 | 91.91 ± 0.16 |
| 59.27 ± 0.31 | 75.06 ± 0.62 | 63.88 ± 0.81 | 71.44 ± 0.67 | 59.56 ± 0.10 | 80.48 ± 0.49 | 82.73 ± 0.24 | 84.11 ± 0.07 | 84.59 ± 0.34 | 87.04 ± 0.21 |
| Gabor | CoTF | BOVW | DCAE | EPLS | SCNN | A-ConvNet | MFFN-GAP | MSCP | MFFN-CPMN | |
|---|---|---|---|---|---|---|---|---|---|---|
| Open land | 66.93 ± 0.38 | 76.18 ± 0.88 | 81.65 ± 1.44 | 67.64 ± 0.28 | 80.34 ± 0.75 | 85.37 ± 1.05 | 91.55 ± 0.49 | 86.48 ± 0.11 | 85.71 ± 0.62 | 86.39 ± 0.03 |
| Road | 43.53 ± 0.54 | 67.57 ± 0.49 | 80.28 ± 0.44 | 74.82 ± 0.26 | 68.64 ± 0.43 | 88.93 ± 0.52 | 93.13 ± 1.20 | 83.62 ± 0.53 | 84.48 ± 0.95 | 89.35 ± 0.27 |
| Water | 57.64 ± 0.04 | 92.12 ± 1.32 | 87.57 ± 0.62 | 92.80 ± 0.12 | 87.87 ± 0.40 | 84.33 ± 0.74 | 85.79 ± 0.12 | 97.15 ± 0.93 | 98.46 ± 0.05 | 98.68 ± 0.09 |
| Runway | 84.13 ± 0.55 | 96.30 ± 0.77 | 97.11 ± 1.01 | 96.09 ± 1.11 | 95.00 ± 0.37 | 97.90 ± 1.03 | 97.41 ± 0.39 | 99.88 ± 0.93 | 99.68 ± 0.43 | 99.93 ± 0.39 |
| Woodland | 60.83 ± 0.60 | 79.51 ± 0.39 | 78.91 ± 0.21 | 77.93 ± 0.54 | 77.22 ± 1.23 | 69.78 ± 0.42 | 72.21 ± 0.67 | 85.71 ± 0.01 | 86.25 ± 0.95 | 89.64 ± 0.23 |
| Residential | 70.47 ± 0.65 | 91.43 ± 0.58 | 81.97 ± 1.05 | 87.53 ± 1.03 | 76.29 ± 0.92 | 94.58 ± 0.55 | 85.14 ± 0.22 | 88.61 ± 1.22 | 91.38 ± 0.37 | 93.00 ± 0.05 |
| Commercial | 96.54 ± 0.95 | 97.92 ± 0.89 | 95.59 ± 0.34 | 96.79 ± 0.90 | 92.65 ± 0.23 | 77.90 ± 0.22 | 76.77 ± 1.00 | 99.11 ± 0.11 | 99.38 ± 0.18 | 99.54 ± 0.06 |
| OA | 67.27 ± 0.44 | 78.88 ± 0.41 | 82.25 ± 0.11 | 72.74 ± 0.23 | 80.28 ± 0.39 | 83.20 ± 0.10 | 87.41 ± 0.25 | 87.41 ± 0.07 | 87.51 ± 0.33 | 88.37 ± 0.07 |
| AA | 68.58 ± 0.08 | 85.87 ± 0.31 | 86.17 ± 0.80 | 84.80 ± 0.49 | 82.57 ± 0.32 | 85.54 ± 0.54 | 86.00 ± 0.87 | 91.51 ± 0.19 | 92.15 ± 0.13 | 93.79 ± 0.18 |
| 48.60 ± 0.23 | 64.43 ± 0.37 | 68.84 ± 0.27 | 57.24 ± 0.38 | 65.57 ± 0.45 | 70.01 ± 0.14 | 76.15 ± 0.39 | 77.05 ± 0.14 | 76.67 ± 0.41 | 78.94 ± 0.11 |
| Gabor | CoTF | BOVW | DCAE | EPLS | SCNN | A-ConvNet | MFFN-GAP | MSCP | MFFN-CPMN | |
|---|---|---|---|---|---|---|---|---|---|---|
| Water | 95.45 ± 1.01 | 93.48 ± 0.15 | 89.43 ± 0.36 | 95.21 ± 0.46 | 93.30 ± 0.39 | 95.08 ± 0.46 | 92.95 ± 0.85 | 95.44 ± 0.45 | 96.65 ± 0.56 | 95.91 ± 0.55 |
| Residential | 86.76 ± 1.25 | 90.25 ± 0.39 | 88.11 ± 0.33 | 92.05 ± 0.43 | 85.94 ± 0.47 | 85.66 ± 0.02 | 94.06 ± 0.39 | 91.90 ± 0.27 | 95.02 ± 0.14 | 95.47 ± 0.20 |
| Vegetation | 78.13 ± 0.83 | 95.19 ± 0.22 | 88.23 ± 0.12 | 92.56 ± 0.22 | 84.84 ± 0.54 | 93.71 ± 0.14 | 93.99 ± 0.51 | 95.71 ± 0.16 | 95.65 ± 0.43 | 96.29 ± 0.31 |
| Open land | 92.45 ± 0.41 | 85.75 ± 0.76 | 94.62 ± 0.57 | 93.63 ± 0.87 | 92.11 ± 0.73 | 97.42 ± 1.03 | 99.17 ± 0.49 | 97.51 ± 0.12 | 97.16 ± 0.22 | 97.71 ± 0.33 |
| OA | 83.40 ± 0.76 | 91.90 ± 0.31 | 90.08 ± 0.14 | 92.84 ± 0.54 | 87.14 ± 0.48 | 93.90 ± 0.69 | 95.49 ± 0.28 | 95.80 ± 0.32 | 96.02 ± 0.29 | 96.61 ± 0.23 |
| AA | 88.20 ± 1.10 | 91.17 ± 0.44 | 90.10 ± 0.24 | 93.36 ± 0.64 | 89.05 ± 0.35 | 92.97 ± 0.58 | 95.04 ± 0.57 | 95.14 ± 0.24 | 96.12 ± 0.37 | 96.35 ± 0.18 |
| 72.43 ± 1.02 | 85.48 ± 0.27 | 82.94 ± 0.17 | 87.42 ± 0.67 | 78.24 ± 0.66 | 89.29 ± 0.64 | 92.06 ± 0.33 | 92.59 ± 0.29 | 92.97 ± 0.41 | 93.99 ± 0.26 |
| Accuracy | Gaofen-3 | Airborne | F-SAR | |
|---|---|---|---|---|
| With Transfer | OA | 0.8641 | 0.8701 | 0.9573 |
| AA | 0.8799 | 0.9102 | 0.9493 | |
| Kappa | 0.8246 | 0.7645 | 0.9248 | |
| Without Transfer | OA | 0.8772 | 0.8741 | 0.9661 |
| AA | 0.8927 | 0.9151 | 0.9635 | |
| Kappa | 0.8411 | 0.7705 | 0.9399 |
| Accuracy | TerraSAR-X | Airborne | F-SAR | |
|---|---|---|---|---|
| With Transfer | OA | 0.8574 | 0.8805 | 0.9604 |
| AA | 0.8556 | 0.9211 | 0.9552 | |
| Kappa | 0.8024 | 0.7815 | 0.9300 | |
| Without Transfer | OA | 0.8673 | 0.8741 | 0.9661 |
| AA | 0.8711 | 0.9151 | 0.9635 | |
| Kappa | 0.8162 | 0.7705 | 0.9399 |
| Accuracy | Gaofen-3 | TerraSAR-X | F-SAR | |
|---|---|---|---|---|
| With Transfer | OA | 0.8563 | 0.8553 | 0.9609 |
| AA | 0.8727 | 0.8549 | 0.9561 | |
| Kappa | 0.8148 | 0.7999 | 0.9308 | |
| Without Transfer | OA | 0.8772 | 0.8673 | 0.9661 |
| AA | 0.8927 | 0.8711 | 0.9635 | |
| Kappa | 0.8411 | 0.8162 | 0.9399 |
| Accuracy | Gaofen-3 | TerraSAR-X | Airborne | |
|---|---|---|---|---|
| With Transfer | OA | 0.8536 | 0.8544 | 0.8357 |
| AA | 0.8690 | 0.8571 | 0.8688 | |
| Kappa | 0.8116 | 0.7989 | 0.7115 | |
| Without Transfer | OA | 0.8772 | 0.8673 | 0.8741 |
| AA | 0.8927 | 0.8711 | 0.9151 | |
| Kappa | 0.8411 | 0.8162 | 0.7705 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, W.; Wu, Y.; Li, M.; Cao, Y.; Hu, X. High-Resolution SAR Image Classification Using Multi-Scale Deep Feature Fusion and Covariance Pooling Manifold Network. Remote Sens. 2021, 13, 328. https://doi.org/10.3390/rs13020328
Liang W, Wu Y, Li M, Cao Y, Hu X. High-Resolution SAR Image Classification Using Multi-Scale Deep Feature Fusion and Covariance Pooling Manifold Network. Remote Sensing. 2021; 13(2):328. https://doi.org/10.3390/rs13020328
Chicago/Turabian StyleLiang, Wenkai, Yan Wu, Ming Li, Yice Cao, and Xin Hu. 2021. "High-Resolution SAR Image Classification Using Multi-Scale Deep Feature Fusion and Covariance Pooling Manifold Network" Remote Sensing 13, no. 2: 328. https://doi.org/10.3390/rs13020328
APA StyleLiang, W., Wu, Y., Li, M., Cao, Y., & Hu, X. (2021). High-Resolution SAR Image Classification Using Multi-Scale Deep Feature Fusion and Covariance Pooling Manifold Network. Remote Sensing, 13(2), 328. https://doi.org/10.3390/rs13020328