1. Introduction
Scene classification plays an essential role in the semantic understanding of Remote Sensing (RS) images by classifying each image into different categories according to its contents [
1]. It provides valuable support to applications ranging from land use and land cover (LULC) determination [
2,
3], environmental monitoring [
4], urban planning [
5,
6], and deforestation mapping [
7].
In the past few years, deep learning-based approaches [
8,
9,
10,
11,
12] have achieved human-level performance on certain RS scene classification benchmarks [
1,
13,
14,
15]. Despite the remarkable achievements, these excellent methods are data-hungry in order to learn massive parameters and often fail when encountering the natural conditions that humans face in the real world—data is not always enough. For instance, consider training a traditional classifier to identify a novel category that has never existed in the current RS scene datasets, e.g., a bicycle-sharing parking lot, a new scene that has recently emerged in China. One would have to first collect hundreds or thousands of relevant RS images taken from the air and space. The high cost of collecting and annotating hinders many downstream applications where data is inherently rare or expensive. Moreover, a trained deep learning model usually struggles when asked to solve a new task unless it re-executes the training process with high computational cost. In contrast, humans can learn new concepts quickly from just one or a handful of examples by drawing upon previous knowledge and experience [
16]. These issues motivated research on Few-Shot Learning (FSL) [
17,
18,
19]—a learning paradigm that emulates human learning—the ability to learn and adapt to new environments rapidly. Specifically, the contemporary FSL setting [
17,
18,
19,
20] is designed to mimic a low-data scenario. Focusing on few-shot classification tasks, we are dealing with two sets of categories—base set (SEEN) and novel set (UNSEEN)—that disjoint in the label space. A successful FSL learner needs to exploit transferable knowledge in the base set, which has sufficient labeled data, and leverage it to build a classifier that generalizes well on UNSEEN categories when provided with extremely few labeled instances per category, e.g., one or five images. Recent research generally addresses the FSL problem by following the idea of meta-learning, i.e., broadening the learner’s scope to batches of related tasks/episodes rather than batches of data points, and gains experience across the tasks. This episodic training scheme is also referred to as “learning-to-learn” by leveraging the experience to improve future learning performance.
The recent success of few-shot learning has captured attention in the remote sensing community. Rußwurm et al. [
21] evaluate a well-known meta-learning algorithm, Model-Agnostic Meta-Learning (MAML) [
19], for land cover few-shot classification problems. They observe that MAML outperforms the traditional transfer learning methods. The work [
22] adopts deep few-shot learning to handle the small sample size problem in hyperspectral image classification. Most previous RS scene few-shot classification methods [
23,
24,
25,
26] fall under the umbrella of metric learning and are built upon Prototypical Networks (ProtoNet) [
18]. RS-MetaNet [
25] improves ProtoNet with a new balance loss that combines the maximum generalization loss and the cross-entropy loss. Zhang et al. [
23] present a meta-learning framework based on ProtoNet and use cosine distance with a learnable scale parameter to achieve better performance. Later on, Discriminative Learning of Adaptive Match Network (DLA-MatchNet) [
27] couples the attention technique and Relation Network [
28], where the former aims to exploit discriminative regions while the latter learns the similarity scores between the images by an adaptive matcher. Zhang et al. [
26] propose an approach named Self-Supervision Equipped with Knowledge Distillation (SSKD) by adopting a self-supervision strategy to drive the network digging the most discriminative category-specific region and boost the performance by a round of self-knowledge distillation. While these methods have achieved significant progress in RS few-shot classification, we observe that these approaches do suffer from two distinct limitations.
One missing piece of the puzzle is that these metric-based algorithms mainly focus on identifying a suitable similarity measure or construct a combined loss function to drive the parameter updates while overlooking the importance of the embedding network. DLA-MatchNet [
27] introduces an attention mechanism in the feature learning stage to capture attention features from channels and spatial dimensions. RS-SSKD [
26] weaves self-supervision into a two-branch network to dig the base-set data fully by refining the pretraining embedding. Both methods aim at learning the most relevant regions to achieve better embeddings. On the other hand, we must pay attention to the inherent characteristics of remote sensing data. For example, as the RS scene images are taken from a top view, the ground objects vary from small sizes such as airplanes to large regions like a forest or meadow. Moreover, under a spatial resolution range from about 30 to 0.2 m per pixel (e.g., the NWPU-RESISC45 dataset [
15]), irrelevant objects inevitably exist in the RS scene images (see
Figure 1). These issues may drive the embeddings from the same category far apart in a given metric space. If we have sufficient training samples, this problem can be greatly alleviated by a deeper neural network. However, we are dealing with a low data regime of the FSL setting, where the embedding network is either too shallow to leverage the model’s expressive capacity or too deep and results in overfitting [
29]. That is the reason why Conv-4 [
17,
18,
19,
28], Resnet-12, and Resnet-18 [
30] are the most popular embedding networks in the FSL world.
The other concern is that the existing models generally project all instances from various tasks into a single common embedding space indiscriminately [
23,
24,
25,
26,
27]. Such strategy implies that the discovered knowledge, i.e., embedded visual features learned on the SEEN categories, are equally useful for any downstream target classification tasks derived from UNSEEN categories. We argue that the issue of which features are the most discriminative to a specific target task has not received considerable attention. For instance, consider that we have two separate classification tasks: “freeway” vs. “forest” and “freeway” vs. “bridge”. It is intuitive that these two tasks use a diverse set of the most discriminative features. Therefore, the ideal embedding model would first need to extract discriminative features for either task simultaneously, which is challenging. Since the current model does not know exactly what the “downstream” target tasks are, it may unexpectedly emphasize unimportant features for later use. Further, even if two sets of discriminative features are extracted, they do not certainly lead to the best performance for a specific target task. For example, the most useful feature to distinguish “freeway” vs. “forest” may be irrelevant to the task of distinguishing “freeway” vs. “bridge”. Naturally, we expect the embedding spaces to be separated, each of which is customized to the target task so that the extracted visual features are the most discriminative.
Figure 2 schematically illustrates the difference between task-agnostic and task-adaptive embeddings.
To sum up, we suggest that the embedding module is crucial due to its dual roles—representing inputs and constructing classifiers in the embedding space. Several recent studies [
31,
32,
33] have supported this assumption with a series of experiments and verified that better embeddings lead to better few-shot learning performance. The question is, how do we get a good embedding? We answer this question by solving two challenges: (1) design a lightweight embedding network that tackles the problems posed by the inherent characteristics of RS scene images; and (2) construct an embedding adaptation module that tailors the common embeddings into adaptive embeddings according to a specific target task. See
Section 3.3 and
Section 3.4 for details.
Our main contributions in this paper are summarized as follows:
We develop an efficacious meta-learning scheme that utilizes two insights to improve few-shot classification performance: a lightweight embedding network that captures multiscale information and a task-adaptive strategy that further refines the embeddings.
We present a new embedding network—Dynamic Kernel Fusion Network (DKF-Net)—that dynamically fuses feature representations from multiple kernels while preserving comparably lightweight customization for few-shot learning.
We propose a novel embedding adaptation module that transforms the universal embeddings obtained from the base set into task-adaptive embeddings via a self-attention architecture. This is achieved by a set-to-set function that contextualizes the instances over a set to ensure that each has strong co-adaptation.
The experimental results on two remote sensing scene datasets demonstrate that our framework surpasses other state-of-the-art approaches. Furthermore, we offer extensive ablation studies to show how the choices in our training scheme impact the few-shot classification performance.
The rest of this paper is organized as follows. We review the related work in
Section 2. The problem setting and the proposed framework are formally described in
Section 3. We report the experimental results in
Section 4 and discuss with ablation studies in
Section 5. Finally,
Section 6 concludes the paper.
2. Related Work
Current few-shot learning has been primarily addressed in the meta-learning manner, where a model is optimized through batches of training episodes/tasks rather than batches of data points, which is referred to as episodic training [
17]. We can roughly divide the existing works on FSL into two groups. (1) Optimization-based methods search for more transferable representations with sensitive parameters that could rapidly adapt to new tasks in the meta-test stage within a few gradient descent steps. MAML [
19], Reptile [
34], LEO [
35], and MetaOptNet [
36] are the most representative approaches in this family. (2) Metric-based methods mainly learn to represent input data in an appropriate embedding space, where a query sample is easy to classify with a distance-based prediction rule. One can measure the distance in the embedding space by simple distance functions such as cosine similarity (e.g., Matching Network [
17]) or Euclidean distance (e.g., Protypical Networks [
18]), or learn parameterized metrics via an auxiliary network (e.g., Relation Network [
28]). Later, in DSN-MR [
37], all samples and metrics are operated in affine subspaces. SAML [
38] suggests the global embeddings are not discriminative enough as dominant objects may locate anywhere on images. The authors tackle this problem by a “collect-and-select” strategy that aligns the relevant local regions between query and support images in a relation matrix. Given the local feature sets generated by two images, DeepEMD [
39] shoots the same problem by employing the Earth Mover’s Distance [
40] to capture their structural similarity. Our work falls within the second group but differs from them in two ways.
First, like SAML and DeepEMD, Tian et al. [
33] also suggest that the core of improving FSL lies in learning more discriminative embedding. In response, contemporary approaches address this challenge either refining the pretraining strategy to exploit the base-set data fully [
33], leveraging self-supervision to feed auxiliary versions of original images into the embedding network [
41], or applying self-distillation to achieve an additional boost [
26]. While these approaches effectively make the embedding more representative, they tend to concentrate too much on designing a complex loss function [
26,
41] or building networks to capture relevant local features at the cost of computing resources and time [
38,
39]. On the contrary, our solution offers a lightweight embedding network that generates more discriminative representations while imposing fewer parameters than the most popular backbone, i.e., ResNet-12 [
30,
36], in few-shot learning. A fundamental property of neurons present in the visual cortex is changing their receptive fields (RF) in response to the stimulus [
42]. This mechanism of adaptively adjusting receptive fields can be incorporated in neural networks by multiscale feature aggregation and selection, which would benefit constructing a desirable RS scene few-shot classification algorithm—considering that the ground objects vary largely in size. Inspired by Selective Kernel (SK) Networks [
43], we introduce a nonlinear procedure for fusing features from multiple kernels in the same layer by a self-attention mechanism. We incorporate two-branch SK convolution into our embedding network and name it Dynamic Kernel Fusion Network (DKF-Net).
Second, the abovementioned methods assume all samples are embedded into a task-agnostic space, hoping the embeddings could sufficiently represent the support data such that the similarities predicted from simple nonparametric classifiers will generalize well to new tasks. We suggest that ideal embedding spaces for few-shot learning should be separated, where each of them is customized to the target task adaptively so that the extracted visual features are discriminative. Some recent works also pay attention to this assumption. TADAM [
44] proposes to learn a task-dependent metric space by constructing a conditional learner on the task-level set and optimizing with an auxiliary task cotraining procedure. TapNet [
45] constructs a projection space for each episode/task and introduces additional reference vectors, in which the class prototypes and the reference vectors are closely aligned. Unfortunately, the task-dependent conditioning mechanism in TADAM requires learning of extra fully connected networks while the projection space in TapNet is solved through the singular value decomposition (SVD) step; both strategies significantly increase training time. Taking inspiration from Transformer [
46], we propose an embedding adaption module based on a self-attention mechanism that transforms “task-agnostic” embeddings into “task-adaptive” embeddings, see
Section 3.4.
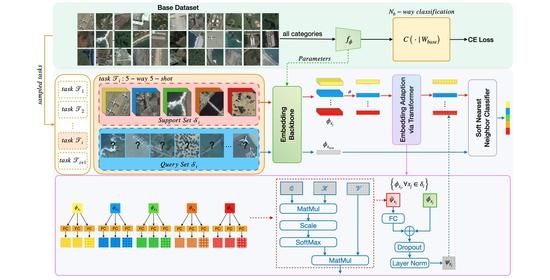
3. Methodology
We now present our approach for the few-shot classification of RS scenes, starting with preliminaries. Then, we present our few-shot learning workflow in
Section 3.2, wherein the overall framework is depicted in
Figure 3. The proposed Dynamic Kernel Fusion Network (DKF-Net) is described in
Section 3.3, the embedding backbone in the whole flow of our work. At last, we elaborate on the embedding adaption module and discuss how it helps few-shot learning in
Section 3.4.
3.1. Preliminaries
Problem setting. In a traditional classification setting, we are given a dataset with categories. terms as the training set, where and are the input image and corresponding label pairs. A predictive model is learned on at training time, and generalization is then evaluated on , i.e., the test set. In few-shot learning (FSL), however, we are dealing with a dataset , divided into three parts with respect to categories: , , and , i.e., training set, validation set, and test set. The category spaces in the three sets are disjointed from each other. The goal of FSL is to learn a general-purpose model on (SEEN) that can generalize well to UNSEEN categories in with one or few training instances per category. In addition, is held out to select the best model.
Episodic training. To mimic the low-data scenario during testing, most of the FSL methods [
17,
18,
19,
28,
36,
47] proceed in a meta-learning fashion. The intuition behind meta-learning is improving the performance of a model by extracting transferable knowledge from a collection of sampled mini-batches called “episodes”, also known as “tasks”, and minimizing the generalization error over a task distribution. Formally, a set of M tasks is denoted as
, sampled from a task distribution
. Each task
can be considered a compact dataset containing both training and test data, referred to as support set
and query set
.
3.2. Overall Framework
The outline of our method to RS scene few-shot classification is: (1) we employ a pretraining stage to learn an embedding model
on the base set
; (2) in the meta-learning stage, we optimize the embedding model with the nearest centroid classifier, in an episodic meta-learning paradigm; and (3) at inference time, i.e., the meta-test stage, the model is fixed, we sample tasks from the novel set
for evaluation and report the mean accuracy. The overview of our method is depicted in
Figure 3. All the stages of our model are built upon the proposed DFK-Net backbone (see
Section 3.3 and
Figure 4). The details of these stages are as follows.
Pretraining stage. We train a base classifier on
to learn a general feature embedding for the downstream meta-leaner, which is helpful to yield robust few-shot classification. The predictive model
, parameterized by
, is trained to classify
base categories (e.g., 25 categories in the NWPU-RESISC45 dataset) in
with the standard cross-entropy (CE) loss, by solving:
The performance of the pretrained model is evaluated after each epoch, based on its 1-shot classification accuracy on the validation set . Specifically, assuming that there are categories in , we randomly sample 200 1-shot -way tasks from to assess the classification performance of the pretrained model and select the best one. The weights of the penultimate layer from the best pretrained model are utilized to initialize the embedding backbone and are optimized in the next meta-learning stage.
Meta-learning stage. In most few-shot learning setups, a model is often evaluated in
N-way
K-shot tasks, where
K is usually very small, e.g.,
or
are the most common settings. Following prior work [
17,
18,
20], an
N-way
K-shot task
is constructed by randomly sampling
N categories, and
K labeled instances per category as the support set
, where
is an image-label pair, and
. We take a fraction of the remaining instances from the same
N categories to form the query set
, and the end goal becomes the classification of the
unlabeled instances into
N categories. Note that
and
are disjointed, i.e.,
while sharing the same label space. Since the pretrained model is trained only on the base set, it often falls into the over-fitting dilemma or is updated very little when facing the novel categories with a meager amount of support instances. Some recent approaches handle this problem by fixing the pretrained model and fine-tune it on the novel set. We adopt an opposite strategy by using a meta-learning paradigm built upon ProtoNet [
18] to optimize the pretrained model
, parameterized by
, directly without introducing any extra parameters.
During the meta-learning stage, we sample a collection of
N-way
K-shot tasks
from
to form the meta-training set
. Likewise, we obtain the meta-validation set
and the meta-test set
from
and
in the same way. Given the meta-training set
, the meta-learning procedure minimizes the generalization error across tasks. Thus, the learning objective can be loosely defined as:
For each
N-way
K-shot task
, there are
K images belonging to category
c in the support set, where
. We define the mean feature of these
K images as the “prototype”
, i.e., the category center, corresponding to category
c:
where
is an embedding function with learnable parameters
, mapping the input
into the feature space. Then, we perform the nearest neighbor classification with the negative Euclidean distance to predict the probability of query instance
belonging to category
c by the following expression:
where
denotes the Euclidean distance. Inspired by prior work [
44], we apply a scale factor,
, to adjust the similarity score, then the above equation becomes:
During the experiments, we tune the initial values of the scale factor empirically and find it affects the meta-learning when the model is optimized based on pretrained weights.
3.3. Dynamic Kernel Fusion Network
We propose the Dynamic Kernel Fusion Network (DKF-Net), a simple yet effective embedding scheme for few-shot learning, to enrich the diversity and expressive capacity of typical backbones, e.g., Conv-4 [
17,
18,
19], ResNet-12, and ResNet-18 [
30]. DKF-Net aims to collect multiscale spatial information by dynamically adjusting the receptive field size of neurons with Selective Kernel (SK) convolutions [
43]. The top of
Figure 4 depicts an SKUnit that is constituted of a
convolution, SK convolution,
convolution}, and the bottom shows the complete DFK-net architecture.
The SK convolution performs dynamic fusion from multiple kernels via three operations —“Split”, “Fuse”, and “Select”. Given a feature map
with
channels and spatial dimensions
, as shown at the top of
Figure 4, we start by constructing two branches built upon transformations
and
, mapping
to feature maps
and
, separately.
and
refer to two convolutional operators with kernels
and
, respectively, and are followed by Batch Normalization (BN) [
48] and ReLU [
49] in sequence. In practice, the
with a
kernel is displaced with a dilated convolutional layer with the rate of 2, which can alleviate further computational burden. This procedure is defined as “Split”.
We expect the neural network can adjust the RF sizes according to the stimulus content adaptively. An instinctive idea is to regulate the information flows from two branches by the second operation—“Fuse”. First, the two branches are initially integrated via element-wise summation, which can be expressed as:
where
is the fused feature. Then,
is passed through a global average pooling (GAP) layer, which produces channel-wise statistic
by shrinking feature maps through their spatial dimensions,
. Formally, if we let
denote the
c-th element of
, it is calculated by:
where
denotes the value at point
of the
c-th channel
. The vector
represents the importance of each channel, and it is further compressed to a compact feature descriptor
to save parameters and reduce dimensionality for better efficiency. Specifically,
is obtained by simply applying a fully connected (FC) layer to
:
represents the fully connected operation defined by weights
, where
refers to the BN [
48] and
denotes the ReLU [
49] function. Thus, the number of channels is reduced to
, where
r indicates the compression ratio and
L is the minimum value of
d. Following previous work [
43,
50], we empirically set
r to 16 and
L to 32.
Finally, the last operation, “Select”, guided by the compact feature descriptor
, is applied to fulfill a dynamic adjustment of multiscale spatial information. This is achieved by a control gate mechanism based on soft attention to assign the importance of each branch across channels. Specifically, let
be the soft attention vectors for
and
; the channel-wise weights can be obtained by applying a softmax operator:
where
,
denotes the
c-th row of
and
denotes the
c-th element of
;
and
are likewise. It is noteworthy that
and
have a relationship of
as there are only two branches in our case. We now have the refined feature map
by applying the attention vectors
and
to each branch along the channel dimension:
where
refers to the
c-th channel of
and
.
The proposed DFK-Net contains four stages with a block of {SK-Unit, ReLU, SK-Unit, ReLU} in each, as illustrated at the bottom of
Figure 4. We set the filters in each stage to 64, 160, 320, and 640, respectively, and add an
GAP layer after the last stage, which outputs 640-dimensional embeddings.
3.4. Embedding Adaption via Transformer
Up until now, the embedding function
, parameterized by
, is assumed to be task-agnostic; we argue that such a setting is not ideal since the knowledge, i.e., the discriminative visual features learned in the base set, are equally effective to any novel categories. Here, we propose an embedding adaptation module that tailors the visual knowledge extracted from the base set, i.e., SEEN categories, into adaptive knowledge according to a specific task. We visualize this concept in
Figure 5 schematically.
Our embedding adaption module is achieved by contextualizing the instances over a set; thus, each of them has strong co-adaptation. Concretely, given a task-agnostic embedding function
, let
denote a set-to-set function that transforms
to a task-adaptive embedding function
. We treat the instances as bags or a set without order, requiring the set-to-set function
to output an adaptive set of instance embeddings while keeping permutation-invariant. The transformation step can be formalized in the following way:
where
is the support set of a target task, and
is a permutation operator over a set that ensures the adapted embeddings will not change regardless of
receiving a set of input instances in any order. Inspired by the Transformer networks [
46], we utilize dot-product self-attention to implement the set-to-set function
. In the following, we use
and
instead of
and
for the sake of notational simplicity.
Following the literature [
46], we can describe the Transformer layer by defining the triplets
to indicate the set of the queries, keys, and values. Note that, in order to avoid the unfortunate double use of the term “query”, we use italics to denote the “query” in the transformer layer to emphasize the difference from the “query set” in the few-shot tasks. Mathematically, in any instance that
belongs to
, we first obtain its query by
, where
is a linear matrix. Similarly, the “key-value” pairs
and
are generated with
and
, respectively. For notion brevity, the bias in the linear projection is omitted here. Next, the similarity between an instance
with others in the support set can be measured by the scaled dot-product attention:
where
d is the dimensionality of the queries and keys. This similarity score then serves as weights for the transformed embedding of
:
where
is the value of the
k-th instance in
. Finally, the task-adaptive embedding is given by:
where
indicates the projection weights of a fully connected layer and
represents a procedure that further transforms the embedding by performing dropout [
51] and layer normalization [
52]. The whole flow of our Transformer module is illustrated on the right side of
Figure 5.
6. Conclusions
This work suggests that embedding is critical to few-shot classification as it plays dual roles—representing images and building classifiers in the embedding space. To this end, we have proposed a framework for a few-shot classification that complements the existing methods by refining the embeddings from two perspectives: a lightweight embedding network that fuses multiscale information and a task-adaptive strategy that further tailors the embeddings. The former enriches the diversity and expressive capacity of embeddings by dynamically weighting information from multiple kernels, while the latter learns discriminative representations by transforming the universal embeddings into task-adaptive embeddings via a self-attention mechanism. We extensively evaluate our model, TAEL, on two datasets: NWPU-RESISC4 and RSD46-WHU. As shown in the results, TAEL outperforms current state-of-the-art methods and comes at a modest training time. Furthermore, the experimental results and ablation studies have verified our assumption that good embeddings positively affect the few-shot classification performance. While our method is effective and the experimental results are encouraging, much work can be done to achieve human-level performance in the low data regime. Our potential future work involves developing algorithms that suit extended settings, e.g., cross-dataset, cross-domain, transductive, and generalized few-shot learning. Another exciting direction for our future work is to extend the standard few-shot learning to a continual setting in which training and testing stages do not have to be separated, and instead, models are evaluated while learning novel concepts as in the real world.