Spatiotemporal Variations in Liquid Water Content in a Seasonal Snowpack: Implications for Radar Remote Sensing
Abstract
:1. Introduction
2. Study Area
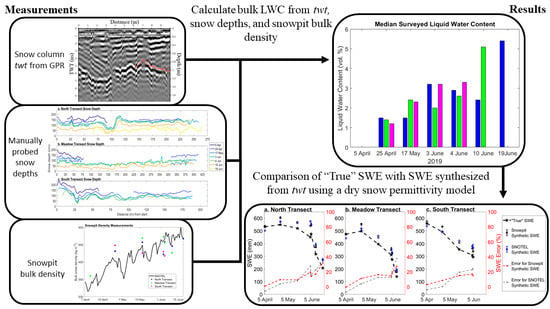
3. Methods
3.1. Nearby Automated Stations
3.2. Observational Period
3.3. Field Methods
3.4. Radargram Processing
3.5. TLS Processing
3.6. LWC Calculations
3.6.1. Probed Snow Depth Adjustments
3.6.2. Constraining Radar Velocity to Calculate LWC
3.7. Synthetic Radar SWE Retrieval Calculations
3.8. Uncertainty in LWC Calculations
4. Results
4.1. Overview of the Study Period
4.2. In Situ Observations
4.3. GPR-Derived LWC
4.4. Sensitivity of Synthetic Radar SWE Retrievals to LWC
5. Discussion
5.1. Variability in GPR and In Situ Observations
5.1.1. Temporal Variability
5.1.2. Spatial Variability
5.2. Implications for Radar Remote Sensing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hammond, J.C.; Saavedra, F.A.; Kampf, S.K. Global snow zone maps and trends in snow persistence 2001–2016. Int. J. Clim. 2018, 38, 4369–4383. [Google Scholar] [CrossRef]
- Kim, E. How Can We Find Out How Much Snow Is in the World? Eos 2018, 99. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Doesken, N.; Judson, A. The Snow Booklet: A Guide to the Science, Climatology, and Measurement of Snow in the United States; Colorado State University: Fort Collins, CO, USA, 1996; p. 86. [Google Scholar]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Keller, F.; Goyette, S.; Beniston, M. Sensitivity Analysis of Snow Cover to Climate Change Scenarios and Their Impact on Plant Habitats in Alpine Terrain. Clim. Chang. 2005, 72, 299–319. [Google Scholar] [CrossRef]
- Niittynen, P.; Heikkinen, R.K.; Luoto, M. Snow cover is a neglected driver of Arctic biodiversity loss. Nat. Clim. Chang. 2018, 8, 997–1001. [Google Scholar] [CrossRef]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424–430. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhang, X.; Zhang, Q.; Lin, Y.; Hao, M.; Luo, Y.; Zhao, Z.; Yao, Y.; Chen, X.; Wang, L.; et al. Recently amplified arctic warming has contributed to a continual global warming trend. Nat. Clim. Chang. 2017, 7, 875–879. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Cayan, D.R.; Meyer, M.K.; Jeton, A.E. Simulated Hydrologic Responses to Climate Variations and Change in the Merced, Carson, and American River Basins, Sierra Nevada, California, 1900–2099. Clim. Chang. 2004, 62, 283–317. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes toward Earlier Streamflow Timing across Western North America. J. Clim. 2005, 18, 1136–1155. [Google Scholar] [CrossRef]
- Clow, D. Changes in the Timing of Snowmelt and Streamflow in Colorado: A Response to Recent Warming. J. Clim. 2010, 23, 2293–2306. [Google Scholar] [CrossRef]
- Hall, D.K.; Crawford, C.J.; DiGirolamo, N.E.; Riggs, G.A.; Foster, J.L. Detection of earlier snowmelt in the Wind River Range, Wyoming, using Landsat imagery, 1972–2013. Remote Sens. Environ. 2015, 162, 45–54. [Google Scholar] [CrossRef]
- Mote, P.W.; Li, S.; Lettenmaier, D.P.; Xiao, M.; Engel, R. Dramatic declines in snowpack in the western US. Npj Clim. Atmos. Sci. 2018, 1. [Google Scholar] [CrossRef]
- Estilow, T.W.; Young, A.H.; Robinson, D.A. A long-term Northern Hemisphere snow cover extent data record for climate studies and monitoring. Earth Syst. Sci. Data 2015, 7, 137–142. [Google Scholar] [CrossRef] [Green Version]
- Klos, P.Z.; Link, T.E.; Abatzoglou, J.T. Extent of the rain-snow transition zone in the western U.S. under historic and projected climate. Geophys. Res. Lett. 2014, 41, 4560–4568. [Google Scholar] [CrossRef]
- Kirkham, J.D.; Koch, I.; Saloranta, T.M.; Litt, M.; Stigter, E.E.; Møen, K.; Thapa, A.; Melvold, K.; Immerzeel, W.W. Near Real-Time Measurement of Snow Water Equivalent in the Nepal Himalayas. Front. Earth Sci. 2019, 7. [Google Scholar] [CrossRef] [Green Version]
- Livneh, B.; Badger, A.M. Drought less predictable under declining future snowpack. Nat. Clim. Chang. 2020, 10, 452–458. [Google Scholar] [CrossRef]
- Dozier, J.; Bair, E.H.; Davis, R.E. Estimating the spatial distribution of snow water equivalent in the world’s mountains. Wiley Interdiscip. Rev. Water 2016, 3, 461–474. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.-P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Mote, T.L.; Grundstein, A.J.; Leathers, D.J.; Robinson, D.A. A comparison of modeled, remotely sensed, and measured snow water equivalent in the northern Great Plains. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Xiong, C.; Jiang, L. Review of snow water equivalent microwave remote sensing. Sci. China Earth Sci. 2016, 59, 731–745. [Google Scholar] [CrossRef]
- Pulliainen, J.; Luojus, K.; Derksen, C.; Mudryk, L.; Lemmetyinen, J.; Salminen, M.; Ikonen, J.; Takala, M.; Cohen, J.; Smolander, T.; et al. Patterns and trends of Northern Hemisphere snow mass from 1980 to 2018. Nat. Cell Biol. 2020, 581, 294–298. [Google Scholar] [CrossRef]
- Painter, T.H.; Berisford, D.F.; Boardman, J.W.; Bormann, K.J.; Deems, J.; Gehrke, F.; Hedrick, A.; Joyce, M.; Laidlaw, R.; Marks, D.; et al. The Airborne Snow Observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef] [Green Version]
- Currier, W.R.; Pflug, J.; Mazzotti, G.; Jonas, T.; Deems, J.S.; Bormann, K.J.; Painter, T.H.; Hiemstra, C.A.; Gelvin, A.; Uhlmann, Z.; et al. Comparing Aerial Lidar Observations with Terrestrial Lidar and Snow-Probe Transects from NASA’s 2017 SnowEx Campaign. Water Resour. Res. 2019, 55, 6285–6294. [Google Scholar] [CrossRef] [Green Version]
- Shean, D.; Alexandrov, O.; Moratto, Z.M.; Smith, B.E.; Joughin, I.; Porter, C.; Morin, P. An automated, open-source pipeline for mass production of digital elevation models (DEMs) from very-high-resolution commercial stereo satellite imagery. ISPRS J. Photogramm. Remote Sens. 2016, 116, 101–117. [Google Scholar] [CrossRef] [Green Version]
- Shaw, T.; Gascoin, S.; Mendoza, P.A.; Pellicciotti, F.; McPhee, J. Snow Depth Patterns in a High Mountain Andean Catchment from Satellite Optical Tristereoscopic Remote Sensing. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Eberhard, L.A.; Sirguey, P.; Miller, A.; Marty, M.; Schindler, K.; Stoffel, A.; Bühler, Y. Intercomparison of photogrammetric platforms for spatially continuous snow depth mapping. Cryosphere 2021, 15, 69–94. [Google Scholar] [CrossRef]
- McGrath, D.; Webb, R.; Shean, D.; Bonnell, R.; Marshall, H.; Painter, T.H.; Molotch, N.P.; Elder, K.; Hiemstra, C.; Brucker, L. Spatially Extensive Ground-Penetrating Radar Snow Depth Observations During NASA’s 2017 SnowEx Campaign: Comparison with In Situ, Airborne, and Satellite Observations. Water Resour. Res. 2019, 55, 10026–10036. [Google Scholar] [CrossRef] [Green Version]
- Harder, P.; Pomeroy, J.W.; Helgason, W.D. Improving sub-canopy snow depth mapping with unmanned aerial vehicles: Lidar versus structure-from-motion techniques. Cryosphere 2020, 14, 1919–1935. [Google Scholar] [CrossRef]
- Deeb, E.J.; Forster, R.R.; Kane, D.L. Monitoring snowpack evolution using interferometric synthetic aperture radar on the North Slope of Alaska, USA. Int. J. Remote Sens. 2011, 32, 3985–4003. [Google Scholar] [CrossRef]
- Marshall, H.P.; Deeb, E.; Forster, R.; Vuyovich, C.; Elder, K.; Hiemstra, C.; Lund, J. L-band InSAR depth retrieval during the NASA SnowEx 2020 campaign: Grand Mesa, Colorado. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021; pp. 625–627. [Google Scholar] [CrossRef]
- Lund, J.; Forster, R.R.; Rupper, S.B.; Deeb, E.J.; Marshall, H.P.; Hashmi, M.Z.; Burgess, E. Mapping Snowmelt Progression in the Upper Indus Basin with Synthetic Aperture Radar. Front. Earth Sci. 2020, 7. [Google Scholar] [CrossRef] [Green Version]
- Huning, L.S.; AghaKouchak, A. Approaching 80 years of snow water equivalent information by merging different data streams. Sci. Data 2020, 7, 333. [Google Scholar] [CrossRef]
- Koch, F.; Prasch, M.; Schmid, L.; Schweizer, J.; Mauser, W. Measuring Snow Liquid Water Content with Low-Cost GPS Receivers. Sensors 2014, 14, 20975–20999. [Google Scholar] [CrossRef] [Green Version]
- Dozier, J.; Shi, J. Estimation of snow water equivalence using SIR-C/X-SAR. I. Inferring snow density and subsurface properties. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2465–2474. [Google Scholar] [CrossRef] [Green Version]
- Moller, D.; Andreadis, K.M.; Bormann, K.J.; Hensley, S.; Painter, T.H. Mapping Snow Depth from Ka-Band Inter-ferometry: Proof of Concept and Comparison with Scanning Lidar Retrievals. IEEE Geosci. Remote Sens. Lett. 2017, 14, 886–890. [Google Scholar] [CrossRef]
- Tsai, Y.-L.S.; Dietz, A.; Oppelt, N.; Kuenzer, C. Remote Sensing of Snow Cover Using Spaceborne SAR: A Review. Remote Sens. 2019, 11, 1456. [Google Scholar] [CrossRef] [Green Version]
- Lievens, H.; Demuzere, M.; Marshall, H.-P.; Reichle, R.H.; Brucker, L.; Brangers, I.; De Rosnay, P.; Dumont, M.; Girotto, M.; Immerzeel, W.W.; et al. Snow depth variability in the Northern Hemisphere mountains observed from space. Nat. Commun. 2019, 10, 4629. [Google Scholar] [CrossRef] [PubMed]
- Marshall, H.P.; Vuyovich, C.; Hiemstra, C.; Brucker, L.; Elder, K.; Deems, J.; Newlin, J. NASA SnowEx 2020 Experiment Plan (Science Plan). 2019. Available online: https://snow.nasa.gov/campaigns/snowex/experimental-plan-2021 (accessed on 23 June 2020).
- Manickam, S.; Barros, A. Parsing Synthetic Aperture Radar Measurements of Snow in Complex Terrain: Scaling Behaviour and Sensitivity to Snow Wetness and Landcover. Remote Sens. 2020, 12, 483. [Google Scholar] [CrossRef] [Green Version]
- Lundberg, A.; Richardson-Näslund, C.; Andersson, C. Snow density variations: Consequences for ground-penetrating radar. Hydrol. Process. 2005, 20, 1483–1495. [Google Scholar] [CrossRef]
- Heilig, A.; Mitterer, C.; Schmid, L.; Wever, N.; Schweizer, J.; Marshall, H.; Eisen, O. Seasonal and diurnal cycles of liquid water in snow—Measurements and modeling. J. Geophys. Res. Earth Surf. 2015, 120, 2139–2154. [Google Scholar] [CrossRef] [Green Version]
- Koh, G.; Yankielun, N.E.; Baptista, A.I. Snow Cover Characterization Using Multiband Fmcw Radars. Hydrol. Process. 1996, 10, 1609–1617. [Google Scholar] [CrossRef]
- Marshall, H.-P.; Koh, G. FMCW radars for snow research. Cold Reg. Sci. Technol. 2008, 52, 118–131. [Google Scholar] [CrossRef]
- Guneriussen, T.; Hogda, K.; Johnsen, H.; Lauknes, I. InSAR for estimation of changes in snow water equivalent of dry snow. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2101–2108. [Google Scholar] [CrossRef]
- Cline, D.W. Snow surface energy exchanges and snowmelt at a continental, midlatitude Alpine site. Water Resour. Res. 1997, 33, 689–701. [Google Scholar] [CrossRef] [Green Version]
- McCabe, G.J.; Clark, M.P.; Hay, L.E. Rain-on-Snow Events in the Western United States. Bull. Am. Meteorol. Soc. 2007, 88, 319–328. [Google Scholar] [CrossRef]
- Jennings, K.S.; Kittel, T.G.F.; Molotch, N.P. Observations and simulations of the seasonal evolution of snowpack cold content and its relation to snowmelt and the snowpack energy budget. Cryosphere 2018, 12, 1595–1614. [Google Scholar] [CrossRef] [Green Version]
- Eiriksson, D.; Whitson, M.; Luce, C.H.; Marshall, H.P.; Bradford, J.; Benner, S.G.; Black, T.; Hetrick, H.; McNamara, J.P. An evaluation of the hydrologic relevance of lateral flow in snow at hillslope and catchment scales. Hydrol. Process. 2013, 27, 640–654. [Google Scholar] [CrossRef]
- Webb, R.W.; Fassnacht, S.R.; Gooseff, M.N.; Webb, S.W. Simulating Water Flow through a Layered Snowpack. Transp. Porous Media 2018, 123, 457–476. [Google Scholar] [CrossRef]
- DeWalle, D.R.; Rango, A. Principles of Snow Hydrology; Cambridge University Press: Cambridge, UK, 2008; p. 410. [Google Scholar]
- Techel, F.; Pielmeier, C. Point observations of liquid water content in wet snow—Investigating methodical, spatial and temporal aspects. Cryosphere 2011, 5, 405–418. [Google Scholar] [CrossRef]
- Schmid, L.; Koch, F.; Heilig, A.; Prasch, M.; Eisen, O.; Mauser, W.; Schweizer, J. A novel sensor combination (upGPR-GPS) to continuously and nondestructively derive snow cover properties. Geophys. Res. Lett. 2015, 42, 3397–3405. [Google Scholar] [CrossRef] [Green Version]
- Webb, R.W.; Williams, M.W.; Erickson, T.A. The Spatial and Temporal Variability of Meltwater Flow Paths: Insights from a Grid of Over 100 Snow Lysimeters. Water Resour. Res. 2018, 54, 1146–1160. [Google Scholar] [CrossRef]
- Webb, R.W.; Wigmore, O.; Jennings, K.; Fend, M.; Molotch, N.P. Hydrologic connectivity at the hillslope scale through intra-snowpack flow paths during snowmelt. Hydrol. Process. 2020, 34, 1616–1629. [Google Scholar] [CrossRef]
- Webb, R.W.; Jennings, K.S.; Fend, M.; Molotch, N.P. Combining Ground-Penetrating Radar With Terrestrial LiDAR Scanning to Estimate the Spatial Distribution of Liquid Water Content in Seasonal Snowpacks. Water Resour. Res. 2018, 54, 10,339–10,349. [Google Scholar] [CrossRef]
- Schmid, L.; Heilig, A.; Mitterer, C.; Schweizer, J.; Maurer, H.; Okorn, R.; Eisen, O. Continuous snowpack monitoring using upward-looking ground-penetrating radar technology. J. Glaciol. 2014, 60, 509–525. [Google Scholar] [CrossRef] [Green Version]
- Bengtsson, L. Percolation of meltwater through a snowpack. Cold Reg. Sci. Technol. 1982, 6, 73–81. [Google Scholar] [CrossRef]
- Webb, R.W.; Fassnacht, S.R.; Gooseff, M.N. Hydrologic flow path development varies by aspect during spring snowmelt in complex subalpine terrain. Cryosphere 2018, 12, 287–300. [Google Scholar] [CrossRef] [Green Version]
- Avanzi, F.; Johnson, R.C.; Oroza, C.A.; Hirashima, H.; Maurer, T.; Yamaguchi, S. Insights into Preferential Flow Snowpack Runoff Using Random Forest. Water Resour. Res. 2019, 55, 10727–10746. [Google Scholar] [CrossRef]
- Sihvola, A.; Tiuri, M. Snow Fork for Field Determination of the Density and Wetness Profiles of a Snow Pack. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 717–721. [Google Scholar] [CrossRef]
- Denoth, A. An electronic device for long-term snow wetness recording. Ann. Glaciol. 1994, 19, 104–106. [Google Scholar] [CrossRef] [Green Version]
- Kawashima, K.; Endo, T.; Takeuchi, Y. A portable calorimeter for measuring liquid-water content of wet snow. Ann. Glaciol. 1998, 26, 103–106. [Google Scholar] [CrossRef] [Green Version]
- Roth, K.; Schulin, R.; Flühler, H.; Attinger, W. Calibration of time domain reflectometry for water content measurement using a composite dielectric approach. Water Resour. Res. 1990, 26, 2267–2273. [Google Scholar] [CrossRef]
- Bradford, J.H.; Harper, J.T.; Brown, J. Complex dielectric permittivity measurements from ground-penetrating radar data to estimate snow liquid water content in the pendular regime. Water Resour. Res. 2009, 45, 12. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fassnacht, S.R.; Brown, K.S.J.; Blumberg, E.J.; Lopez-Moreno, J.I.; Covino, T.P.; Kappas, M.; Huang, Y.; Leone, V.; Kashipazha, A.H. Distribution of snow depth variability. Front. Earth Sci. 2018, 12, 683–692. [Google Scholar] [CrossRef]
- Wake, L.; Marshall, S. Assessment of current methods of positive degree-day calculation using in situ observations from glaciated regions. J. Glaciol. 2015, 61, 329–344. [Google Scholar] [CrossRef] [Green Version]
- Blindow, N. Ground Penetrating Radar. In Groundwater Geophysics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gubler, H.; Weilenmann, P. Seasonal Snow Cover Monitoring Using FMCW Radar. Int. Snow Sci. Workshop 1986, 87–97. Available online: https://arc.lib.montana.edu/snow-science/objects/issw-1986-087-097.pdf (accessed on 23 June 2020).
- Sandmeier, K.J. (2019), Reflexw—GPR and Seismic Processing Software, Sandmeier. Available online: https://www.sandmeier-geo.de/reflexw.html (accessed on 23 June 2020).
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The National Elevation Dataset. Photogramm. Eng. Remote Sens. 2002, 68, 5–11. [Google Scholar]
- Deems, J.S.; Painter, T.H.; Finnegan, D.C. Lidar measurement of snow depth: A review. J. Glaciol. 2013, 59, 467–479. [Google Scholar] [CrossRef] [Green Version]
- Sturm, M.; Holmgren, J. An Automatic Snow Depth Probe for Field Validation Campaigns. Water Resour. Res. 2018, 54, 9695–9701. [Google Scholar] [CrossRef]
- Peinetti, H.R.; Kalkhan, M.A.; Coughenour, M.B. Long-term changes in willow spatial distribution on the elk winter range of Rocky Mountain National Park (USA). Landsc. Ecol. 2002, 17, 341–354. [Google Scholar] [CrossRef]
- Di Paolo, F.; Cosciotti, B.; Lauro, S.E.; Mattei, E.; Pettinelli, E. Dry snow permittivity evaluation from density: A critical review. In Proceedings of the 2018 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 1–5. [Google Scholar]
- Ryan, W.A.; Doesken, N.J.; Fassnacht, S.R. Evaluation of Ultrasonic Snow Depth Sensors for U.S. Snow Measurements. J. Atmos. Ocean. Technol. 2008, 25, 667–684. [Google Scholar] [CrossRef] [Green Version]
- Proksch, M.; Rutter, N.; Fierz, C.; Schneebeli, M. Intercomparison of snow density measurements: Bias, precision, and vertical resolution. Cryosphere 2016, 10, 371–384. [Google Scholar] [CrossRef]
- Marsh, P.; Woo, M.-K. Meltwater Movement in Natural Heterogeneous Snow Covers. Water Resour. Res. 1985, 21, 1710–1716. [Google Scholar] [CrossRef]
- Rasmus, S. Spatial and Temporal Variability of Snow Bulk Density and Seasonal Snow Densification Behavior in Finland. Geophysica 2013, 49, 53–74. [Google Scholar]
- Samimi, S.; Marshall, S.J. Diurnal Cycles of Meltwater Percolation, Refreezing, and Drainage in the Supraglacial Snowpack of Haig Glacier, Canadian Rocky Mountains. Front. Earth Sci. 2017, 5. [Google Scholar] [CrossRef] [Green Version]
- Pomeroy, J.W.; Dion, K. Winter Radiation Extinction and Reflection in a Boreal Pine Canopy: Measurements and Modelling. Hydrol. Process. 1996, 10, 1591–1608. [Google Scholar] [CrossRef]
- Link, T.E.; Marks, D. Point simulation of seasonal snow cover dynamics beneath boreal forest canopies. J. Geophys. Res. Space Phys. 1999, 104, 27841–27857. [Google Scholar] [CrossRef]
- Kattelmann, R. Spatial Variability of Snow-Pack Outflow at a Site in Sierra Nevada, USA. Ann. Glaciol. 1989, 13, 124–128. [Google Scholar] [CrossRef] [Green Version]
- Raleigh, M.S.; Small, E.E. Snowpack density modeling is the primary source of uncertainty when mapping basin-wide SWE with lidar. Geophys. Res. Lett. 2017, 44, 3700–3709. [Google Scholar] [CrossRef]
- Griessinger, N.; Mohr, F.; Jonas, T. Measuring snow ablation rates in alpine terrain with a mobile multioffset ground-penetrating radar system. Hydrol. Process. 2018, 32, 3272–3282. [Google Scholar] [CrossRef]
- López-Moreno, J.; Fassnacht, S.; Heath, J.; Musselman, K.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2013, 55, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Meromy, L.; Molotch, N.P.; Link, T.E.; Fassnacht, S.R.; Rice, R. Subgrid variability of snow water equivalent at operational snow stations in the western US. Hydrol. Process. 2013, 27, 2383–2400. [Google Scholar] [CrossRef]














| Date | Transect | Snowpit | Depth Transect | GPR |
|---|---|---|---|---|
| 5 April | North | Partial | 1 | |
| Meadow | X | Partial | 1 | |
| South | Partial | 1 | ||
| 25 April | North | X | Partial | 3 |
| Meadow | X | Partial | 3 | |
| South | X | Partial | 3 | |
| 17 May | North | X | Complete | 1 |
| Meadow | X | Partial | 1 | |
| South | X | Complete | 3 | |
| 3 June | North | X | Complete | 2 |
| Meadow | X | Complete | 3 | |
| South | X | Complete | 3 | |
| 4 June | North | X | Complete | 3 |
| Meadow | X | Complete | 3 | |
| South | X | Complete | 3 | |
| 10 June | North | X | Complete | 3 |
| Meadow | X | Complete | 3 | |
| South | 0 | |||
| 19 June | North | X | Complete | 3 |
| Meadow | 0 | |||
| South | 0 |
| Date | 30 April | 18 May | 21 May | 29 May | 20 June | 22 June |
|---|---|---|---|---|---|---|
| Precipitation (mm) | 23 | 15 | 13 | 15 | 20 | 13 |
| SWE (mm) | 25.4 | 10.2 | 20.3 | 12.7 | 0 | 20.3 |
| Date | North Transect | Meadow Transect | South Transect |
|---|---|---|---|
| 5 April | 0 | 0 | 0 |
| 25 April | 1.5 | 1.4 | 1.2 |
| 17 May | 1.5 | 2.4 | 2.3 |
| 3 June | 3.2 | 2 | 3.2 |
| 4 June | 2.9 | 2.6 | 3.3 |
| 10 June | 2.4 | 5.1 | No Snow |
| 19 June | 5.4 | No Snow | No Snow |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonnell, R.; McGrath, D.; Williams, K.; Webb, R.; Fassnacht, S.R.; Marshall, H.-P. Spatiotemporal Variations in Liquid Water Content in a Seasonal Snowpack: Implications for Radar Remote Sensing. Remote Sens. 2021, 13, 4223. https://doi.org/10.3390/rs13214223
Bonnell R, McGrath D, Williams K, Webb R, Fassnacht SR, Marshall H-P. Spatiotemporal Variations in Liquid Water Content in a Seasonal Snowpack: Implications for Radar Remote Sensing. Remote Sensing. 2021; 13(21):4223. https://doi.org/10.3390/rs13214223
Chicago/Turabian StyleBonnell, Randall, Daniel McGrath, Keith Williams, Ryan Webb, Steven R. Fassnacht, and Hans-Peter Marshall. 2021. "Spatiotemporal Variations in Liquid Water Content in a Seasonal Snowpack: Implications for Radar Remote Sensing" Remote Sensing 13, no. 21: 4223. https://doi.org/10.3390/rs13214223
APA StyleBonnell, R., McGrath, D., Williams, K., Webb, R., Fassnacht, S. R., & Marshall, H. -P. (2021). Spatiotemporal Variations in Liquid Water Content in a Seasonal Snowpack: Implications for Radar Remote Sensing. Remote Sensing, 13(21), 4223. https://doi.org/10.3390/rs13214223