Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China
Abstract
:1. Introduction
2. Materials and Methods
3. Results
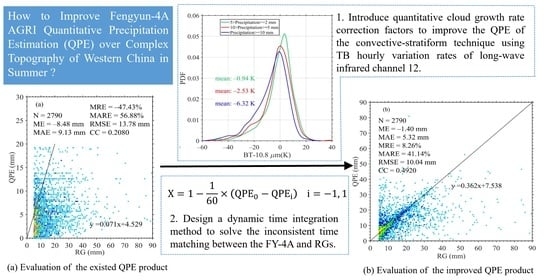
3.1. Validation of NSMC QPE
3.2. Improvement of QPE Algorithm Based on the FY-4A AGRI
3.2.1. Cloud Classification
3.2.2. Improvements of QPE Algorithm
3.3. Validations of Improved QPE Algorithm Based on the FY-4A AGRI
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviate | Full Name |
|---|---|
| AE | auto-estimator |
| AGRI | Advanced Geosynchronous Radiation Imager |
| AVHRR | Advanced Very High Resolution Radiometer |
| CC | correlation coefficient |
| CDF | cumulative distribution function |
| CIMISS | China Integrated Meteorological Information Sharing Service platform |
| CST | convective-stratiform technique |
| FY-2 | Fenyun-2 |
| FY-4A | Fengyun-4A |
| GEO | geostationary |
| GMSRA | GOES multispectral rainfall algorithm |
| GOES-R | Geostationary Operational Environmental Satellite R series |
| GPI | GOES precipitation index |
| HE | hydro-estimator |
| IR | infrared |
| LEO | low earth orbiting |
| LWIR | long-wave infrared |
| LST | local standard time |
| MAE | mean absolute error |
| MARE | mean absolute relative error |
| ME | mean error |
| MICAPS | Meteorological Information Comprehensive Analysis and Processing System |
| MRE | mean relative error |
| MWIR | medium-wave infrared |
| NESDIS | National Environmental Satellite Data and Information Service |
| NOAA | National Oceanic and Atmospheric Administration |
| NSMC | National Satellite Meteorological Center |
| probability density function | |
| QPE | quantitative precipitation estimation |
| RG | rain gauge |
| RMSE | root mean squared error |
| SCaMPR | self-calibrating multivariate precipitation retrieval |
| TB | brightness temperature |
| WV | water vapor |
| VIS | visible |
References
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 228–232. [Google Scholar] [CrossRef]
- Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.; Hong, Y. Global View Of Real-Time Trmm Multisatellite Precipitation Analysis: Implications For Its Successor Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2015, 96, 283–296. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Futrell, J.; Gephart, R.; Kabat-Lensch, E.; McKnight, D.; Pyrtle, A.; Schimel, J.; Smyth, R.; Skole, D.; Wilson, D.; Gephart, J. Water: Challenges at the Intersection of Human and Natural Systems; 2005. Available online: https://www.osti.gov/biblio/1046481 (accessed on 29 October 2021). [CrossRef] [Green Version]
- Council, N.R. When Weather Matters: Science and Services to Meet Critical Societal Needs; National Academies Press: Washington, DC, USA, 2010; pp. 60–70. ISBN 13 978-0-309-15249-5. [Google Scholar]
- Kucera, P.A.; Ebert, E.E.; Turk, F.J.; Levizzani, V.; Kirschbaum, D.; Tapiador, F.J.; Loew, A.; Borsche, M. Precipitation from Space: Advancing Earth System Science. Bull. Am. Meteorol. Soc. 2013, 94, 365–375. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. J. Hydrometeorol. 2007, 8, 758–769. [Google Scholar] [CrossRef]
- Hegerl, G.C.; Black, E.; Allan, R.P.; Ingram, W.J.; Polson, D.; Trenberth, K.E.; Chadwick, R.S.; Arkin, P.A.; Sarojini, B.B.; Becker, A.; et al. Challenges in Quantifying Changes in the Global Water Cycle. Bull. Am. Meteorol. Soc. 2015, 96, 1097–1115. [Google Scholar] [CrossRef] [Green Version]
- Ruhi, A.; Messager, M.L.; Olden, J.D. Tracking the pulse of the Earth’s fresh waters. Nat. Sustain. 2018, 1, 198–203. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- New, M.; Todd, M.; Hulme, M.; Jones, P. Precipitation measurements and trends in the twentieth century. Int. J. Climatol. 2001, 21, 1889–1922. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Woldemeskel, F.M.; Sivakumar, B.; Sharma, A. Merging gauge and satellite rainfall with specification of associated uncertainty across Australia. J. Hydrol. 2013, 499, 167–176. [Google Scholar] [CrossRef]
- Smith, J.A.; Bradley, A.A.; Baeck, M.L. The Space-Time Structure of Extreme Storm Rainfall in the Southern Plains. J. Appl. Meteorol. Climatol. 1994, 33, 1402–1417. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.A.; Seo, D.J.; Baeck, M.L.; Hudlow, M.D. An Intercomparison Study of NEXRAD Precipitation Estimates. Water Resour. Res. 1996, 32, 2035–2045. [Google Scholar] [CrossRef]
- Groisman, P.; Legates, D. The Accuracy of United States Precipitation Data. Bull. Am. Meteorol. Soc. 1994, 75, 215–227. [Google Scholar] [CrossRef]
- Peck, E.L. Quality of Hydrometeorological Data in Cold Regions. JAWRA J. Am. Water Resour. Assoc. 1997, 33, 125–134. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Z.; Tang, G.; Ji, Q.; Min, X.; Wan, W.; Shi, Z. Quantitative evaluations and error source analysis of Fengyun-2-based and GPM-based precipitation products over mainland China in summer, 2018. Remote Sens. 2019, 11, 2992. [Google Scholar] [CrossRef] [Green Version]
- Kitchen, M.; Brown, R.; Davies, A.G. Real-time correction of weather radar data for the effects of bright band, range and orographic growth in widespread precipitation. Q. J. R. Meteorol. Soc. 1994, 120, 1231–1254. [Google Scholar] [CrossRef]
- Westrick, K.J.; Mass, C.F.; Colle, B.A. The Limitations of the WSR-88D Radar Network for Quantitative Precipitation Measurement over the Coastal Western United States. Bull. Am. Meteorol. Soc. 1999, 80, 2289–2298. [Google Scholar] [CrossRef]
- Pellarin, T.; Delrieu, G.; Saulnier, G.-M.; Andrieu, H.; Vignal, B.; Creutin, J.-D. Hydrologic Visibility of Weather Radar Systems Operating in Mountainous Regions: Case Study for the Ard?che Catchment (France). J. Hydrometeorol. 2002, 3, 539–555. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Xu, C.-Y. Assessing the performance of satellite-based precipitation products and its dependence on topography over Poyang Lake basin. Theor. Appl. Climatol. 2014, 115, 713–729. [Google Scholar] [CrossRef]
- Jongjin, B.; Jongmin, P.; Dongryeol, R.; Minha, C. Geospatial blending to improve spatial mapping of precipitation with high spatial resolution by merging satellite-based and ground-based data. Hydrol. Process. 2016, 30, 2789–2803. [Google Scholar] [CrossRef]
- Levizzani, V.; Bauer, P.; Joseph Turk, F. Measuring Precipitation from Space: EURAINSAT and the Future; Springer: Dordrecht, The Netherlands, 2007; Volume 28, pp. 49–58. ISBN 13 978-1-4020-5835-6. [Google Scholar] [CrossRef]
- Shukla, S.; McNally, A.; Husak, G.; Funk, C. A seasonal agricultural drought forecast system for food-insecure regions of East Africa. Hydrol. Earth Syst. Sci. 2014, 18, 3907–3921. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y. Satellite-borne active and passive instruments for remote sensing of heavy rain in China: A review. Torrential Rain Disasters 2019, 38, 554–563. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.F.; Negri, A.; Huffman, G.J. Flood and landslide applications of near real-time satellite rainfall products. Nat. Hazards 2007, 43, 285–294. [Google Scholar] [CrossRef] [Green Version]
- Barrett, E.C. The estimation of monthly rainfall from satellite data. Mon. Weather Rev. 1970, 98, 322–327. [Google Scholar] [CrossRef] [Green Version]
- Arkin, P.A.; Ardanuy, P.E. Estimating climatic-scale precipitation from space: A review. J. Clim. 1989, 2, 1229–1238. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Yu, F.; Zhao, Y. Inversion Study of Rainfall Intensity Field at All Time during Mei-Yu Period by Using MTSAT Multi-spectral Imagery. In Proceedings of the Multispectral, Hyperspectral, and Ultraspectral Remote Sensing Technology, Techniques, and Applications II, Noumea, New Caledonia, 17–21 November 2008; International Society for Optics and Photonics: Washington, DC, USA, 2008; Volume 7149, p. 714918. [Google Scholar] [CrossRef]
- Zhuge, X.-Y.; Yu, F.; Zhang, C.-W. Rainfall Retrieval and Nowcasting Based on Multispectral Satellite Images. Part I: Retrieval Study on Daytime 10-Minute Rain Rate. J. Hydrometeorol. 2011, 12, 1255–1270. [Google Scholar] [CrossRef]
- Negri, A.J.; Adler, R.F. Relation of Satellite-Based Thunderstorm Intensity to Radar-Estimated Rainfall. J. Appl. Meteorol. Climatol. 1981, 20, 288–300. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.F.; Negri, A.J. A Satellite Infrared Technique to Estimate Tropical Convective and Stratiform Rainfall. J. Appl. Meteorol. Climatol. 1988, 27, 30–51. [Google Scholar] [CrossRef] [Green Version]
- Vicente, G.A.; Scofield, R.A.; Menzel, W.P. The Operational GOES Infrared Rainfall Estimation Technique. Bull. Am. Meteorol. Soc. 1998, 79, 1883–1898. [Google Scholar] [CrossRef]
- Arkin, P.A.; Meisner, B.N. The Relationship between Large-Scale Convective Rainfall and Cold Cloud over the Western Hemisphere during 1982–84. Mon. Weather Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef] [Green Version]
- Ba, M.B.; Gruber, A. GOES Multispectral Rainfall Algorithm (GMSRA). J. Appl. Meteorol. 2001, 40, 1500–1514. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef] [Green Version]
- Scofield, R.A. The NESDIS Operational Convective Precipitation- Estimation Technique. Mon. Weather Rev. 1987, 115, 1773–1793. [Google Scholar] [CrossRef]
- Vicente, G.A.; Davenport, J.C.; Scofield, R.A. The role of orographic and parallax corrections on real time high resolution satellite rainfall rate distribution. Int. J. Remote Sens. 2002, 23, 221–230. [Google Scholar] [CrossRef]
- Scofield, R.A.; Kuligowski, R.J. Status and Outlook of Operational Satellite Precipitation Algorithms for Extreme-Precipitation Events. Weather Forecast. 2003, 18, 1037–1051. [Google Scholar] [CrossRef] [Green Version]
- Ronald, S.; Dong, X.; Xi, B.; Feng, Z.; Kuligowski, R. Improving Satellite Quantitative Precipitation Estimates Using GOES-Retrieved Cloud Optical Depth. J. Hydrometeorol. 2015, 17, 557–570. [Google Scholar] [CrossRef]
- Goldenbergl, S.B.; Houze, R.A., Jr.; Churchill, D.D. Convective and stratiform components of a winter monsoon cloud cluster determined from geosynchronous infrared satellite data. J. Meteorol. Soc. Jpn. Ser. II 1990, 68, 37–63. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, L.; Zhou, F. Convective and stratiform cloud rainfall estimation from geostationary satellite data. Adv. Atmos. Sci. 1993, 10, 475–480. [Google Scholar] [CrossRef]
- Bendix, J. Adjustment of the Convective-Stratiform Technique (CST) to estimate 1991/93 El Nino rainfall distribution in Ecuador and Peru by means of Meteosat-3 IR data. Int. J. Remote Sens. 1997, 18, 1387–1394. [Google Scholar] [CrossRef]
- Endarwin, E.; Hadi, S.; Tjasyono, H.K.B.; Gunawan, D.; Siswanto, S. Modified Convective Stratiform Technique (CSTm) Performance on Rainfall Estimation in Indonesia. J. Math. Fundam. Sci. 2014, 46, 251–268. [Google Scholar] [CrossRef] [Green Version]
- Wulandari, A.; Pratama, K.; Ismail, P. Using Convective Stratiform Technique (CST) method to estimate rainfall (case study in Bali, December 14 th 2016). J. Phys. Conf. Ser. 2018, 1022, 012039. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.-L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite-Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef] [Green Version]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauß, T. Precipitation estimates from MSG SEVIRI daytime, nighttime, and twilight data with random forests. J. Appl. Meteorol. Climatol. 2014, 53, 2457–2480. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.; Gao, X.; Ihler, A.; Sorooshian, S.; Hsu, K. Precipitation identification with bispectral satellite information using deep learning approaches. J. Hydrometeorol. 2017, 18, 1271–1283. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X. RF-MEP: A novel Random Forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Tapakis, R.; Charalambides, A. Equipment and methodologies for cloud detection and classification: A review. Sol. Energy 2013, 95, 392–430. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the new generation of Chinese geostationary weather satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Cheng, L.; Bao, J.-W. Numerical Simulation of the 1981 Sichuan Flood. Part I: Evolution of a Mesoscale Southwest Vortex. Mon. Weather Rev. 1988, 116, 2481–2504. [Google Scholar] [CrossRef] [Green Version]
- Ren, D. The devastating Zhouqu Storm-triggered debris flow of August 2010: Likely causes and possible trends in a future warming climate. J. Geophys. Res. Atmos. 2014, 119, 3643–3662. [Google Scholar] [CrossRef]
- Kabeja, C.; Li, R.; Guo, J.; Rwatangabo, D.E.R.; Manyifika, M.; Gao, Z.; Wang, Y.; Zhang, Y. The Impact of Reforestation Induced Land Cover Change (1990–2017) on Flood Peak Discharge Using HEC-HMS Hydrological Model and Satellite Observations: A Study in Two Mountain Basins, China. Water 2020, 12, 1347. [Google Scholar] [CrossRef]
- Gu, X.; Liao, L.; Duan, Y.; Yu, F. Characteristics of rainstorm with different time scales in Guizhou during 2020 flood season. Torrential Rain Disasters 2020, 39, 586–592. [Google Scholar] [CrossRef]
- Li, G.; Chen, J. New progresses in the research of heavy rain vortices formed over the southwest China. Torrential Rain Disasters 2018, 37, 293–302. [Google Scholar] [CrossRef]
- Cui, C.; Dong, X.; Wang, B.; Yang, H. Phase Two of the Integrative Monsoon Frontal Rainfall Experiment (IMFRE-II) over the Middle and Lower Reaches of the Yangtze River in 2020; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of high-resolution satellite precipitation products over China. J. Geophys. Res. Atmos. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Ebert, E.E. Methods for verifying satellite precipitation estimates. In Measuring Precipitation from Space; Springer: Berlin/Heidelberg, Germany, 2007; pp. 345–356. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Collopy, F. Error measures for generalizing about forecasting methods: Empirical comparisons. Inter. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Twycross, J.; Garibaldi, J.M. A new accuracy measure based on bounded relative error for time series forecasting. PLoS ONE 2017, 12, e0174202. [Google Scholar] [CrossRef] [Green Version]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Jia, S.F.; Lv, A.F.; Zhu, W.B.; Gao, Y.C. Precision estimation of the average daily precipitation simulated by IPCC AR5 GCMs in China. J. Geo-Inf. Sci. 2016, 18, 227–237. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.L.; Hong, Y.; Wang, J.H.; Gourley, J.J.; Jiang, S.H.; Chen, X.; Wang, W. Hydrologic evaluation of Multisatellite Precipitation Analysis standard precipitation products in basins beyond its inclined latitude band: A case study in Laohahe basin, China. Water Resour. Res. 2010, 46, W07542. [Google Scholar] [CrossRef] [Green Version]
- Kuligowski, R.J.; Li, Y.; Hao, Y.; Zhang, Y. Improvements to the GOES-R Rainfall Rate Algorithm. J. Hydrometeorol. 2016, 17, 1693–1704. [Google Scholar] [CrossRef]
- Ren, J.; Huang, Y.; Guan, L.; Ye, J.; Ni, T. Application of FY-2 Satellite Data in Radar Rainfall Estimation. Remote Sens. Inf. 2017, 32, 39–44. [Google Scholar] [CrossRef]
- Li, J.; Fengxian, Z. Computer identification of multispectral satellite cloud imagery. Adv. Atmos. Sci. 1990, 7, 366–375. [Google Scholar] [CrossRef]
- Pilewskie, P.; Twomey, S. Discrimination of ice from water in clouds by optical remote sensing. Atmos. Res. 1987, 21, 113–122. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Gutman, G. Retrieving microphysical properties near the tops of potential rain clouds by multispectral analysis of AVHRR data. Atmos. Res. 1994, 34, 259–283. [Google Scholar] [CrossRef]
- Lensky, I.M.; Rosenfeld, D. Estimation of precipitation area and rain intensity based on the microphysical properties retrieved from NOAA AVHRR data. J. Appl. Meteorol. Climatol. 1997, 36, 234–242. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. Delineation of raining from non-raining clouds during nighttime using Meteosat-8 data. Meteorol. Appl. 2008, 15, 219–230. [Google Scholar] [CrossRef]







| Channel Number | Central Wavelength/μm | Spatial Resolution/km | Temporal Resolution/min | Channel Name |
|---|---|---|---|---|
| C009 | 6.25 | 4.0 | 5~15 | WV |
| C010 | 7.1 | 4.0 | 5~15 | WV |
| C011 | 8.5 | 4.0 | 5~15 | LWIR |
| C012 | 10.8 | 4.0 | 5~15 | LWIR |
| C013 | 12.0 | 4.0 | 5~15 | LWIR |
| C014 | 13.5 | 4.0 | 5~15 | LWIR |
| Statistical Index | Unit | Formula | Best Value |
|---|---|---|---|
| Mean Error (ME) | mm | 0 | |
| Mean Absolute Error (MAE) | mm | 0 | |
| Mean Relative Error (MRE) | % | 0 | |
| Mean Absolute Relative Error (MARE) | % | 0 | |
| Root Mean Squared Error (RMSE) | mm | 0 | |
| Correlation Coefficient (CC) | NA | 1 |
| Water/Land Surface (K) | Low Level Clouds (K) | Middle Level Clouds (K) | Altostratus/ Nimbostratus Clouds (K) | Cirrostratus Clouds (K) | Cirrus Spissatus Clouds (K) | Convective Clouds (K) | |
|---|---|---|---|---|---|---|---|
| C009 | 241 | 238 | 237 | 235 | 231 | 225 | 215 |
| C010 | 254 | 251 | 248 | 245 | 239 | 230 | 217 |
| C011 | 288 | 280 | 270 | 260 | 250 | 236 | 219 |
| C012 | 290 | 281 | 270 | 260 | 248 | 234 | 217 |
| C013 | 288 | 278 | 268 | 258 | 246 | 232 | 216 |
| C014 | 261 | 257 | 252 | 246 | 238 | 228 | 216 |
| C009−C014 | −20 | −19 | −15 | −11 | −7 | −3 | −1 |
| C009−C013 | −47 | −40 | −31 | −23 | −15 | −7 | −1 |
| C009−C012 | −50 | −42 | −33 | −25 | −17 | −9 | −2 |
| C009−C011 | −48 | −41 | −33 | −25 | −19 | −11 | −4 |
| C009−C010 | −13 | −12 | −11 | −10 | −8 | −5 | −2 |
| C010−C012 | −37 | −30 | −22 | −15 | −10 | −4 | 0 |
| C011−C014 | 27 | 22 | 18 | 14 | 12 | 8 | 3 |
| C012−C014 | 29 | 23 | 18 | 14 | 10 | 6 | 1 |
| C013−C014 | 27 | 21 | 16 | 12 | 8 | 4 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Xu, G.; Zhang, W.; Leng, L.; Xiao, Y.; Wan, R.; Wang, J. Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China. Remote Sens. 2021, 13, 4366. https://doi.org/10.3390/rs13214366
Ren J, Xu G, Zhang W, Leng L, Xiao Y, Wan R, Wang J. Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China. Remote Sensing. 2021; 13(21):4366. https://doi.org/10.3390/rs13214366
Chicago/Turabian StyleRen, Jing, Guirong Xu, Wengang Zhang, Liang Leng, Yanjiao Xiao, Rong Wan, and Junchao Wang. 2021. "Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China" Remote Sensing 13, no. 21: 4366. https://doi.org/10.3390/rs13214366
APA StyleRen, J., Xu, G., Zhang, W., Leng, L., Xiao, Y., Wan, R., & Wang, J. (2021). Evaluation and Improvement of FY-4A AGRI Quantitative Precipitation Estimation for Summer Precipitation over Complex Topography of Western China. Remote Sensing, 13(21), 4366. https://doi.org/10.3390/rs13214366