Depths Inferred from Velocities Estimated by Remote Sensing: A Flow Resistance Equation-Based Approach to Mapping Multiple River Attributes at the Reach Scale
Abstract
:1. Introduction
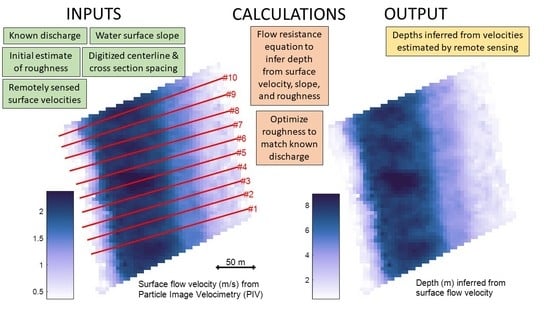
- Introduce the Depths Inferred from Velocities Estimated by Remote Sensing (DIVERS) framework for calculating depths from remotely sensed velocities via a flow resistance equation that expresses depth as a function of velocity, slope, and roughness.
- Evaluate the potential of this approach by conducting a case study on a large, sediment-laden river in Alaska, the Tanana.
- Assess the suitability of a power law-based flow resistance equation for inferring depth from velocity by applying the relation directly to field measurements.
- Scale up a PIV-based workflow developed based on an image time series acquired from a helicopter hovering at a single location above the channel to a larger reach by applying the procedure to multiple hovers distributed along the river.
- Compare different methods of setting the roughness parameter, including per-hover or reach-aggregated flow resistance optimization (FRO) to match a known discharge.
- Quantify the accuracy of velocities, depths, and discharges inferred from remotely sensed data via comparison to field measurements.
2. Materials and Methods
2.1. Study Area
2.2. Remotely Sensed Data
2.3. Field Data
2.4. Particle Image Velocimetry (PIV)
- Acquire video while hovering above the channel, select the frame rate to retain for analysis, extract the corresponding sequence of images, and convert the images from RGB to grayscale;
- Geo-reference the first image in the stabilized stack to a suitable base image. Tie points are used to define an affine transformation that is applied to each image to project the stack into a common real world coordinate system;
- Prepare the images for PIV by using FIJI to apply a finite Fourier transform bandpass filter and a histogram equalization contrast stretch;
- Extract the actual spatial footprint of each frame by outlining the boundary of the non-zero pixels in the image;
- Overlay the footprints of all the images in the stack to identify the area of common coverage and digitize a region of interest (ROI) for PIV;
- Crop all of the images in the stack to a common bounding box based on the digitized ROI and apply a binary raster mask to each image to obtain a series of co-registered, pre-processed, water-only images for PIV;
- Perform the PIV analysis using the ensemble correlation algorithm included within PIVlab, a widely used add-in to MATLAB developed by Thielicke and Stamhuis [39,40]. PIV settings to be specified by the user include the size (in pixels) of the interrogation area within which feature displacements are estimated by computing correlations between successive images and the step size that controls the spacing of the velocity vectors output from PIVlab. In this study, a fixed interrogation area of 64 pixels and a step size of 32 pixels was used to process all of the hovers;
- Post-process the PIV output by discarding spurious vectors that fall below a minimum velocity threshold, differ from the mean velocity magnitude by more than three standard deviations, or fail to pass a normalized median check [39]. To fill any gaps resulting from these filters and obtain continuous coverage, the remaining vectors are linearly interpolated;
- Scale the PIV output by using the ground sampling distance of the images (0.15 m in this study) to establish the number of pixels per meter and multiplying by the frame rate (1 Hz for this study) to obtain velocities in m/s. The geo-referencing information for the stack also is used to transform the vectors to the same real world coordinate system as the images.
2.5. Depths Inferred from Velocities Estimated by Remote Sensing (DIVERS): A Flow Resistance Equation-Based Framework for Calculating Depth from Surface Velocity
2.6. Application to the Tanana River
2.7. Accuracy Assessment
3. Results
3.1. Application of the Flow Resistance Equation to Field Measurements
3.2. Image Stabilization and Geo-Referencing
3.3. Reach-Scale Mapping of Flow Velocities
3.4. DIVERS Output from a Single Hover
3.5. Reach-Aggregated Flow Resistance Optimization
3.6. Accuracy Assessment Summary and Comparison of Approaches
4. Discussion
4.1. A Field Test of the DIVERS Framework
4.2. Spatial Variations in Performance and Limitations of the Flow Resistance Equation
4.3. Different Versions of DIVERS and Potential for Reach-Scale Mapping
4.4. Future Research Directions
5. Conclusions
- The DIVERS framework is based upon a number of critical assumptions that limit its applicability and performance. The flow is treated as steady, uniform, and one-dimensional, with no cross-stream transfer of mass or momentum. Moreover, DIVERS involves applying a flow resistance equation that is typically used to characterize bulk, cross-sectionally averaged hydraulics to calculate depths on a per-pixel basis. In essence, each node of the PIV output grid is considered in isolation such that the water depth at a given location is directly proportional to the local flow velocity and is not influenced by adjacent grid nodes.
- Application of the DIVERS framework to field data resulted in modest agreement between observed and predicted depths ( = 0.51 for the entire reach and 0.61 for a single transect in a straight section of the channel) and many large underestimates of depth, implying that the inherent limitations of the approach might constrain the accuracy with which depths can be inferred from remotely sensed velocities.
- Agreement between velocities measured directly in the field and estimated from remotely sensed data via PIV varied from hover to hover within the reach, with OP values ranging from 0.22 to 0.97 and a median value of 0.57. PIV-based velocities, which were not adjusted to convert surface velocities to depth-averaged velocities, did not consistently over-or under-predict the field observations. The median normalized mean bias was −2.7% and the median RMSE was 16.6%. These results suggest that velocities estimated by tracking naturally occurring sediment boil vortices were reasonably accurate and precise.
- For a single hover in a straight section, agreement between depths inferred via DIVERS and field measurements was stronger (OP of 0.78), with a smaller mean and standard deviation of errors than when DIVERS was applied to field data. Plotting a cross section illustrated the direct proportionality between PIV-derived velocities and depths calculated via DIVERS.
- Depth estimates were more accurate for a per-hover flow resistance optimization (FRO) approach (median normalized median bias of −4%) than for reach-aggregated FRO (10%). The precision of the two DIVERS variants was quantified in terms of the normalized RMSE, with values of 37% and 48% for the per-hover and reach-aggregated FRO methods, respectively.
- The FRO algorithm successfully reproduced the discharge recorded at a gaging station to within a median of 1% on a per-hover basis and within 4% when cross sections were aggregated over the entire reach. The median normalized RMSE values for the discharge estimates from these approaches were 10% for per-hover FRO and 20% for reach-aggregated FRO.
- Although the assumptions inherent to the DIVERS framework impose some important limitations, this study demonstrated the potential of this approach to provide plausible, first-order approximations of water depth throughout the reach. These estimates could be refined through further research focused on incorporating more sophisticated numerical modeling techniques that account for processes, such as lateral transfer of momentum in meander bends, that are not represented in the initial iteration of DIVERS.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADCP | Acoustic Doppler current profiler |
| ASK | A priori specification of k |
| DIVERS | Depths inferred from velocities estimated by remote sensing |
| FRO | Flow resistance optimization |
| GPS | Global positioning system |
| IMU | Inertial motion unit |
| NWIS | National Water Information System |
| OP | Observed vs./predicted |
| PIV | Particle image velocimetry |
| ROI | Region of interest |
| SSC | Suspended sediment concentration |
| UAS | Unmanned aircraft system |
| USGS | United States Geological Survey |
| XS | Cross section |
References
- Conaway, J.; Eggleston, J.; Legleiter, C.; Jones, J.; Kinzel, P.; Fulton, J. Remote sensing of river flow in Alaska—New technology to improve safety and expand coverage of USGS streamgaging. U. S. Geol. Surv. Fact Sheet 2019, 2019, 4. [Google Scholar] [CrossRef] [Green Version]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.A. Satellite remote sensing estimation of river discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef] [Green Version]
- Altenau, E.H.; Pavelsky, T.M.; Moller, D.; Pitcher, L.H.; Bates, P.D.; Durand, M.T.; Smith, L.C. Temporal variations in river water surface elevation and slope captured by AirSWOT. Remote Sens. Environ. 2019, 224, 304–316. [Google Scholar] [CrossRef] [Green Version]
- Gleason, C.J.; Durand, M.T. Remote Sensing of River Discharge: A Review and a Framing for the Discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef] [Green Version]
- Legleiter, C.J.; Kinzel, P.J.; Nelson, J.M. Remote measurement of river discharge using thermal particle image velocimetry (PIV) and various sources of bathymetric information. J. Hydrol. 2017, 554, 490–506. [Google Scholar] [CrossRef]
- Fulton, J.W.; Mason, C.A.; Eggleston, J.R.; Nicotra, M.J.; Chiu, C.L.; Henneberg, M.F.; Best, H.R.; Cederberg, J.R.; Holnbeck, S.R.; Lotspeich, R.R.; et al. Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages. Remote Sens. 2020, 12, 1296. [Google Scholar] [CrossRef] [Green Version]
- Kinzel, P.; Legleiter, C. sUAS-Based Remote Sensing of River Discharge Using Thermal Particle Image Velocimetry and Bathymetric Lidar. Remote Sens. 2019, 11, 2317. [Google Scholar] [CrossRef] [Green Version]
- Fulton, J.W.; Anderson, I.E.; Chiu, C.L.; Sommer, W.; Adams, J.D.; Moramarco, T.; Bjerklie, D.M.; Fulford, J.M.; Sloan, J.L.; Best, H.R.; et al. QCam: sUAS-Based Doppler Radar for Measuring River Discharge. Remote Sens. 2020, 12, 3317. [Google Scholar] [CrossRef]
- Bandini, F.; Sunding, T.P.; Linde, J.; Smith, O.; Jensen, I.K.; Köppl, C.J.; Butts, M.; Bauer-Gottwein, P. Unmanned Aerial System (UAS) observations of water surface elevation in a small stream: Comparison of radar altimetry, LIDAR and photogrammetry techniques. Remote Sens. Environ. 2020, 237, 111487. [Google Scholar] [CrossRef]
- Legleiter, C.; Kinzel, P.J. Inferring Surface Flow Velocities in Sediment-Laden Alaskan Rivers from Optical Image Sequences Acquired from a Helicopter. Remote Sens. 2020, 12, 1282. [Google Scholar] [CrossRef] [Green Version]
- Dugan, J.P.; Anderson, S.P.; Piotrowski, C.C.; Zuckerman, S.B. Airborne Infrared Remote Sensing of Riverine Currents. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3895–3907. [Google Scholar] [CrossRef]
- Muste, M.; Fujita, I.; Hauet, A. Large-scale particle image velocimetry for measurements in riverine environments. Water Resour. Res. 2008, 44, W00D19. [Google Scholar] [CrossRef] [Green Version]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Surface flow measurements from drones. J. Hydrol. 2016, 540, 240–245. [Google Scholar] [CrossRef] [Green Version]
- Pearce, S.; Ljubičić, R.; Peña-Haro, S.; Perks, M.; Tauro, F.; Pizarro, A.; Dal Sasso, S.; Strelnikova, D.; Grimaldi, S.; Maddock, I.; et al. An Evaluation of Image Velocimetry Techniques under Low Flow Conditions and High Seeding Densities Using Unmanned Aerial Systems. Remote Sens. 2020, 12, 232. [Google Scholar] [CrossRef] [Green Version]
- Strelnikova, D.; Paulus, G.; Käfer, S.; Anders, K.H.; Mayr, P.; Mader, H.; Scherling, U.; Schneeberger, R. Drone-Based Optical Measurements of Heterogeneous Surface Velocity Fields around Fish Passages at Hydropower Dams. Remote Sens. 2020, 12, 384. [Google Scholar] [CrossRef] [Green Version]
- Eltner, A.; Sardemann, H.; Grundmann, J. Technical Note: Flow velocity and discharge measurement in rivers using terrestrial and unmanned-aerial-vehicle imagery. Hydrol. Earth Syst. Sci. 2020, 24, 1429–1445. [Google Scholar] [CrossRef] [Green Version]
- Tosi, F.; Rocca, M.; Aleotti, F.; Poggi, M.; Mattoccia, S.; Tauro, F.; Toth, E.; Grimaldi, S. Enabling Image-Based Streamflow Monitoring at the Edge. Remote Sens. 2020, 12, 2047. [Google Scholar] [CrossRef]
- Perks, M.T. KLT-IV v1.0: Image velocimetry software for use with fixed and mobile platforms. Geosci. Model Dev. Discuss. 2020, 13, 6111–6130. [Google Scholar] [CrossRef]
- Lin, D.; Grundmann, J.; Eltner, A. Evaluating Image Tracking Approaches for Surface Velocimetry With Thermal Tracers. Water Resour. Res. 2019, 55, 3122–3136. [Google Scholar] [CrossRef]
- Legleiter, C.; Harrison, L.R. Remote Sensing of River Bathymetry: Evaluating a Range of Sensors, Platforms, and Algorithms on the Upper Sacramento River, California, USA. Water Resour. Res. 2019, 55, 2142–2169. [Google Scholar] [CrossRef]
- Bandini, F.; Lüthi, B.; Peña-Haro, S.; Borst, C.; Liu, J.; Karagkiolidou, S.; Hu, X.; Lemaire, G.G.; Bjerg, P.L.; Bauer-Gottwein, P. A Drone-Borne Method to Jointly Estimate Discharge and Manning’s Roughness of Natural Streams. Water Resour. Res. 2021, 57, e2020WR028266. [Google Scholar] [CrossRef]
- Legleiter, C.; Kinzel, P. Helicopter-based videos and field measurements of flow depth and velocity from the Tanana River, Alaska, acquired on 24 Jul 2019. U. S. Geol. Surv. Data Release 2021, 12, 1282. [Google Scholar] [CrossRef]
- USGS National Water Information System: USGS 15515500 TANANA R AT NENANA AK. Available online: https://waterdata.usgs.gov/nwis/inventory/?site_no=15515500 (accessed on 11 May 2021).
- Wada, T.; Chikita, K.A.; Kim, Y.; Kudo, I. Glacial Effects on Discharge and Sediment Load in the Subarctic Tanana River Basin, Alaska. Arctic Antarct. Alp. Res. 2011, 43, 632–648. [Google Scholar] [CrossRef] [Green Version]
- Chickadel, C.C.; Horner-Devine, A.R.; Talke, S.A.; Jessup, A.T.C.L. Vertical boil propagation from a submerged estuarine sill. Geophys. Res. Lett. 2009, 36, L10601. [Google Scholar] [CrossRef] [Green Version]
- Talke, S.A.; Horner-Devine, A.R.; Chickadel, C.C.; Jessup, A.T. Turbulent kinetic energy and coherent structures in a tidal river. J. Geophys. Res. Ocean. 2013, 118, 6965–6981. [Google Scholar] [CrossRef] [Green Version]
- Fujita, I.; Komura, S. Application of Video Image Analysis for Measurements of River-Surface Flows. Proc. Hydraul. Eng. JSCE 1994, 38, 733–738. [Google Scholar] [CrossRef]
- Fujita, I.; Hino, T. Unseeded and Seeded PIV Measurements of River Flows Videotaped from a Helicopter. J. Vis. 2003, 6, 245–252. [Google Scholar] [CrossRef]
- DJI Zenmuse X5. Available online: https://www.dji.com/zenmuse-x5 (accessed on 13 April 2021).
- Teledyne Marine RiverRay ADCP. Available online: http://www.teledynemarine.com/riverray-adcp?ProductLineID=13 (accessed on 13 April 2021).
- Hemisphere GNSS A101 Smart Antenna User Guide. Available online: https://www.hemispheregnss.com/wp-content/uploads/2019/01/hemispheregnss_a101_userguide_875-0324-000_b1.pdf (accessed on 13 April 2021).
- Parsons, D.R.; Jackson, P.R.; Czuba, J.A.; Engel, F.L.; Rhoads, B.L.; Oberg, K.A.; Best, J.L.; Mueller, D.S.; Johnson, K.K.; Riley, J.D. Velocity Mapping Toolbox (VMT): A processing and visualization suite for moving-vessel ADCP measurements. Earth Surf. Process. Landforms 2013, 38, 1244–1260. [Google Scholar] [CrossRef]
- Mueller, D.S. extrap: Software to assist the selection of extrapolation methods for moving-boat ADCP streamflow measurements. Comput. Geosci. 2013, 54, 211–218. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Kinzel, P.J. Surface Flow Velocities From Space: Particle Image Velocimetry of Satellite Video of a Large, Sediment-Laden River. Front. Water 2021, 3, 652213. [Google Scholar] [CrossRef]
- Mueller, D.S. QRev—Software for Computation and Quality Assurance of Acoustic Doppler Current Profiler Moving-Boat Streamflow Measurements—User’s Manual for Version 2.8. In U. S. Geological Survey Open-File Report 2016-1052; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2016. [Google Scholar] [CrossRef] [Green Version]
- Mueller, D.S. QRev—Software for Computation and Quality Assurance of Acoustic Doppler Current profiler Moving-Boat Streamflow Measurements—Technical Manual for Version 2.8. In U. S. Geological Survey Open-File Report 2016-1068; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Cardona, A.; Saalfeld, S.; Schindelin, J.; Arganda-Carreras, I.; Preibisch, S.; Longair, M.; Tomancak, P.; Hartenstein, V.; Douglas, R.J. TrakEM2 Software for Neural Circuit Reconstruction. PLoS ONE 2012, 7, e38011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- FIJI-ImageJ. Available online: https://imagej.net/Fiji (accessed on 14 April 2021).
- Thielicke, W.; Stamhuis, E.J. PIVlab—Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef] [Green Version]
- Thielicke, W.; Stamhuis, E.J. PIVlab-Time-Resolved Digital Particle Image Velocimetry Tool for MATLAB. Figshare Dataset 2019, 12, 1092508.v19. [Google Scholar]
- Nelson, J.M.; Bennett, S.J.; Wiele, S.M. Flow and sediment transport modeling. In Tools in Fluvial Geomorphology; Kondolf, G.M., Piegay, H., Eds.; Wiley: New York, NY, USA, 2003; pp. 539–576. [Google Scholar]
- Smart, G.M.; Biggs, H.J. Remote gauging of open channel flow: Estimation of depth averaged velocity from surface velocity and turbulence. Proc. River Flow 2020, 2020, 1–10. [Google Scholar]
- Le Coz, J.; Hauet, A.; Pierrefeu, G.; Dramais, G.; Camenen, B. Performance of image-based velocimetry (LSPIV) applied to flash-flood discharge measurements in Mediterranean rivers. J. Hydrol. 2010, 394, 42–52. [Google Scholar] [CrossRef] [Green Version]
- Kinzel, P.J.; Legleiter, C.J.; Nelson, J.M.; Conaway, J.S.; LeWinter, A.L.; Gadomski, P.J.; Filiano, D. Near-field remote sensing of Alaska Rivers. In Proceedings of the 2019 Federal Interagency Sedimentation and Hydrologic Modeling Conference (SEDHYD), Reno, NV, USA, 24–28 June 2019. [Google Scholar]
- Ferguson, R. Flow resistance equations for gravel- and boulder-bed streams. Water Resour. Res. 2007, 43, W05427. [Google Scholar] [CrossRef] [Green Version]
- Legleiter, C. Calibrating remotely sensed river bathymetry in the absence of field measurements: Flow REsistance Equation-Based Imaging of River Depths (FREEBIRD). Water Resour. Res. 2015, 51, 2865–2884. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]
- Pineiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Global Mapper-All-in-one GIS Software. 2020. Available online: https://www.bluemarblegeo.com/products/global-mapper.php (accessed on 15 April 2021).
- Toniolo, H. Bed Forms and Sediment Characteristics along the Thalweg on the Tanana River near Nenana, Alaska, USA. Nat. Resour. 2013, 4, 20–30. [Google Scholar] [CrossRef] [Green Version]
- van Rijn, L.C. Sediment Transport, Part III: Bed forms and Alluvial Roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]















| Hover | n | OP | OP int. | OP Slope | Bias (m/s) | RMSE (m/s) | Norm. Bias | Norm. RMSE |
|---|---|---|---|---|---|---|---|---|
| 51 | 81 | 0.898 | 0.079 | 0.989 | −0.062 | 0.222 | −0.041 | 0.147 |
| 52 | 60 | 0.869 | 0.179 | 0.888 | 0.018 | 0.227 | 0.010 | 0.129 |
| 53 | 61 | 0.549 | −0.390 | 1.091 | 0.223 | 0.563 | 0.121 | 0.305 |
| 54 | 70 | 0.390 | 0.614 | 0.667 | −0.022 | 0.452 | −0.012 | 0.254 |
| 55 | 26 | 0.547 | 0.549 | 0.639 | 0.184 | 0.258 | 0.090 | 0.127 |
| 56 | 48 | 0.974 | 0.194 | 0.994 | −0.187 | 0.231 | −0.164 | 0.202 |
| 57 | 0 | |||||||
| 58 | 43 | 0.926 | 0.221 | 0.945 | −0.145 | 0.215 | −0.105 | 0.156 |
| 59 | 0 | |||||||
| 60 | 56 | 0.887 | 0.107 | 0.983 | −0.081 | 0.185 | −0.056 | 0.128 |
| 61 | 118 | 0.381 | 0.437 | 0.764 | −0.154 | 0.468 | −0.129 | 0.390 |
| 62 | 93 | 0.502 | 0.179 | 0.992 | −0.170 | 0.373 | −0.136 | 0.300 |
| 63 | 62 | 0.599 | −0.070 | 1.049 | 0.008 | 0.220 | 0.007 | 0.176 |
| 64 | 29 | 0.221 | 0.514 | 0.539 | 0.082 | 0.202 | 0.064 | 0.157 |
| Median | 58 | 0.574 | 0.187 | 0.964 | −0.042 | 0.229 | −0.027 | 0.166 |
| Hover | k Method | n XS | Fit k (m) | n | OP | OP int. | OP Slope | Norm. Bias | Norm. RMSE |
|---|---|---|---|---|---|---|---|---|---|
| 51 | Per-hover | 8 | 0.000708 | 84 | 0.751 | −0.636 | 1.101 | 0.039 | 0.277 |
| 52 | Per-hover | 9 | 0.003242 | 61 | 0.627 | −0.779 | 1.247 | −0.122 | 0.358 |
| 53 | Per-hover | 9 | 0.002227 | 64 | 0.758 | −0.624 | 1.131 | −0.024 | 0.330 |
| 54 | Per-hover | 10 | 0.000619 | 70 | 0.430 | 2.436 | 0.481 | 0.086 | 0.384 |
| 55 | Per-hover | 7 | 0.000303 | 26 | 0.400 | 3.097 | 0.349 | −0.152 | 0.338 |
| 56 | Per-hover | 5 | 0.000420 | 48 | 0.614 | −1.207 | 1.019 | 0.249 | 0.430 |
| 57 | Per-hover | 9 | 0.000359 | ||||||
| 58 | Per-hover | 10 | 0.001289 | 44 | 0.783 | −0.016 | 0.878 | 0.125 | 0.254 |
| 59 | Per-hover | 10 | 0.001803 | ||||||
| 60 | Per-hover | 9 | 0.001078 | 56 | 0.634 | 2.284 | 0.553 | −0.125 | 0.495 |
| 61 | Per-hover | 6 | 0.001062 | 118 | 0.425 | 1.360 | 0.694 | −0.083 | 0.573 |
| 62 | Per-hover | 4 | 0.005958 | 93 | 0.320 | 3.364 | 0.458 | −0.104 | 0.594 |
| 63 | Per-hover | 4 | 0.001248 | 62 | 0.536 | 2.268 | 0.264 | 0.161 | 0.772 |
| 64 | Per-hover | 4 | 0.000597 | 29 | 0.597 | 1.038 | 0.642 | −0.056 | 0.209 |
| Median | Per-hover | 8.5 | 0.001070 | 62 | 0.606 | 1.199 | 0.668 | −0.040 | 0.371 |
| Aggregated | Reach-agg. | 104 | 0.001 | 712 | 0.452 | 1.691 | 0.539 | 0.099 | 0.483 |
| Hover | k Method | XS | Q error (m/s) | Q RMSE (m/s) | Norm. Error (%) | Norm. RMSE (%) |
|---|---|---|---|---|---|---|
| 51 | Per-hover | 8 | 7.63 | 114.44 | 0.44 | 6.65 |
| 52 | Per-hover | 9 | 18.78 | 179.69 | 1.09 | 10.44 |
| 53 | Per-hover | 9 | 121.75 | 457.99 | 7.07 | 26.60 |
| 54 | Per-hover | 10 | 63.71 | 331.29 | 3.70 | 19.24 |
| 55 | Per-hover | 7 | 11.07 | 138.55 | 0.64 | 8.05 |
| 56 | Per-hover | 5 | 3.32 | 76.20 | 0.19 | 4.43 |
| 57 | Per-hover | 9 | 9.74 | 129.44 | 0.57 | 7.52 |
| 58 | Per-hover | 10 | 7.70 | 115.35 | 0.45 | 6.70 |
| 59 | Per-hover | 10 | 17.90 | 175.50 | 1.04 | 10.19 |
| 60 | Per-hover | 9 | 18.22 | 176.75 | 1.06 | 10.26 |
| 61 | Per-hover | 6 | 27.37 | 217.22 | 1.59 | 12.61 |
| 62 | Per-hover | 4 | 19.85 | 184.85 | 1.15 | 10.73 |
| 63 | Per-hover | 4 | 18.04 | 176.28 | 1.05 | 10.24 |
| 64 | Per-hover | 4 | 2.33 | 63.88 | 0.14 | 3.71 |
| Median | Per-hover | 8.5 | 17.97 | 175.89 | 1.04 | 10.21 |
| Aggregated | Reach-agg. | 104 | 71.99 | 352.04 | 4.18 | 20.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Legleiter, C.; Kinzel, P. Depths Inferred from Velocities Estimated by Remote Sensing: A Flow Resistance Equation-Based Approach to Mapping Multiple River Attributes at the Reach Scale. Remote Sens. 2021, 13, 4566. https://doi.org/10.3390/rs13224566
Legleiter C, Kinzel P. Depths Inferred from Velocities Estimated by Remote Sensing: A Flow Resistance Equation-Based Approach to Mapping Multiple River Attributes at the Reach Scale. Remote Sensing. 2021; 13(22):4566. https://doi.org/10.3390/rs13224566
Chicago/Turabian StyleLegleiter, Carl, and Paul Kinzel. 2021. "Depths Inferred from Velocities Estimated by Remote Sensing: A Flow Resistance Equation-Based Approach to Mapping Multiple River Attributes at the Reach Scale" Remote Sensing 13, no. 22: 4566. https://doi.org/10.3390/rs13224566
APA StyleLegleiter, C., & Kinzel, P. (2021). Depths Inferred from Velocities Estimated by Remote Sensing: A Flow Resistance Equation-Based Approach to Mapping Multiple River Attributes at the Reach Scale. Remote Sensing, 13(22), 4566. https://doi.org/10.3390/rs13224566