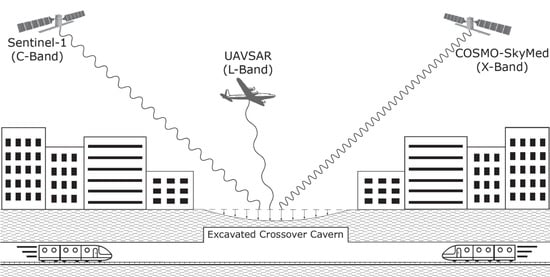
Mapping Urban Excavation Induced Deformation in 3D via Multiplatform InSAR Time-Series
Abstract
:1. Introduction
2. Study Area
3. Data and Methods
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Burgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic aperture radar interferometry to measure earth’s surface topography and its deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodríguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A review of interferometric synthetic aperture RADAR (InSAR) multi-track approaches for the retrieval of Earth’s Surface displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef] [Green Version]
- Short, N.; Brisco, B.; Couture, N.; Pollard, W.; Murnaghan, K.; Budkewitsch, P. A comparison of TerraSAR-X, RADARSAT-2 and ALOS-PALSAR interferometry for monitoring permafrost environments, case study from Herschel Island, Canada. Remote Sens. Environ. 2011, 115, 3491–3506. [Google Scholar] [CrossRef]
- Wempen, J.M.; McCarter, M.K. Comparison of L-band and X-band differential interferometric synthetic aperture radar for mine subsidence monitoring in central Utah. Int. J. Min. Sci. Technol. 2017, 27, 159–163. [Google Scholar] [CrossRef]
- Lu, Y.; Ke, C.Q.; Zhou, X.; Wang, M.; Lin, H.; Chen, D.; Jiang, H. Monitoring land deformation in Changzhou city (China) with multi-band InSAR data sets from 2006 to 2012. Int. J. Remote Sens. 2018, 39, 1151–1174. [Google Scholar] [CrossRef]
- Solari, L.; Ciampalini, A.; Raspini, F.; Bianchini, S.; Zinno, I.; Bonano, M.; Manunta, M.; Moretti, S.; Casagli, N. Combined use of C- and X-band SAR data for subsidence monitoring in an urban area. Geosciences 2017, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Du, Z.; Ge, L.; Li, X.; Ng, A.H.-M. Subsidence monitoring over the Southern Coalfield, Australia using both L-Band and C-Band SAR time series analysis. Remote Sens. 2016, 8, 543. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Wang, C.; Long, Y.; Yi, Z. Analysis of the decadal kinematic characteristics of the Daguangbao landslide using multi-platform time series InSAR observations after the Wenchuan earthquake. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019325. [Google Scholar] [CrossRef]
- Qu, T.; Xu, Q.; Liu, C.; Li, Z.; Chen, B.; Dai, K. Radar remote sensing applications in landslide monitoring with multi-platform insar observations: A case study from China. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2019, 42, 1939–1943. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Yu, J.; Chen, B.; Wang, Y. Urban subsidence monitoring by SBAS-InSAR technique with multi-platform SAR images: A case study of Beijing Plain, China. Eur. J. Remote Sens. 2020, 53, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Solano-Rojas, D.E.; Wdowinski, S.; Cabral-Cano, E.; Osmanoglu, B.; Havazli, E.; Pacheco-Martioónez, J. A multiscale approach for detection and mapping differential subsidence using multi-platform InSAR products. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 173–177. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Hu, F.; Tianliang, Y. Ground subsidece monitoring along the levee of Huangpu River by multi-platform high-resolution SAR images. In Proceedings of the 2016 4th International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Guangzhou, China, 4–6 July 2016. [Google Scholar]
- Bekaert, D.P.S.; Jones, C.E.; An, K.; Huang, M.H. Exploiting UAVSAR for a comprehensive analysis of subsidence in the Sacramento Delta. Remote Sens. Environ. 2019, 220, 124–134. [Google Scholar] [CrossRef]
- Serrano-Juan, A.; Pujades, E.; Vázquez-Suñè, E.; Crosetto, M.; Cuevas-González, M. Leveling vs. InSAR in urban underground construction monitoring: Pros and cons. Case of la sagrera railway station (Barcelona, Spain). Eng. Geol. 2017, 218, 1–11. [Google Scholar] [CrossRef]
- Motagh, M.; Djamour, Y.; Walter, T.R.; Wetzel, H.U.; Zschau, J.; Arabi, S. Land subsidence in Mashhad Valley, northeast Iran: Results from InSAR, levelling and GPS. Geophys. J. Int. 2007, 168, 518–526. [Google Scholar] [CrossRef]
- Bürgmann, R.; Hilley, G.; Ferretti, A.; Novali, F. Resolving vertical tectonics in the San Francisco Bay Area from permanent scatterer InSAR and GPS analysis. Geology 2006, 34, 221–224. [Google Scholar] [CrossRef] [Green Version]
- Catalão, J.; Nico, G.; Hanssen, R.; Catita, C. Merging GPS and atmospherically corrected InSAR data to map 3-D terrain displacement velocity. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2354–2360. [Google Scholar] [CrossRef] [Green Version]
- Henderson, S.T.; Pritchard, M.E. Time-dependent deformation of Uturuncu volcano, Bolivia, constrained by GPS and InSAR measurements and implications for source models. Geosphere 2017, 13, 1834–1854. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Ding, X.L.; Li, Z.W.; Zhang, L.; Zhu, J.J.; Sun, Q.; Gao, G.J. Vertical and horizontal displacements of Los Angeles from InSAR and GPS time series analysis: Resolving tectonic and anthropogenic motions. J. Geodyn. 2016, 99, 27–38. [Google Scholar] [CrossRef]
- Poland, M.P.; Bürgmann, R.; Dzurisin, D.; Lisowski, M.; Masterlark, T.; Owen, S.; Fink, J. Constraints on the mechanism of long-term, steady subsidence at Medicine Lake volcano, northern California, from GPS, leveling, and InSAR. J. Volcanol. Geotherm. Res. 2006, 150, 55–78. [Google Scholar] [CrossRef]
- Akbarimehr, M.; Motagh, M.; Haghshenas-Haghighi, M. Slope stability assessment of the sarcheshmeh landslide, northeast Iran, investigated using InSAR and GPS observations. Remote Sens. 2013, 5, 3681–3700. [Google Scholar] [CrossRef] [Green Version]
- Dzurisin, D.; Lisowski, M.; Wicks, C.W. Continuing inflation at Three Sisters volcanic center, central Oregon Cascade Range, USA, from GPS, leveling, and InSAR observations. Bull. Volcanol. 2009, 71, 1091–1110. [Google Scholar] [CrossRef]
- Xue, X.; Freymueller, J.; Lu, Z. Modeling the Posteruptive Deformation at Okmok Based on the GPS and InSAR Time Series: Changes in the Shallow Magma Storage System. J. Geophys. Res. Solid Earth 2020, 125, e2019JB017801. [Google Scholar] [CrossRef]
- Papoutsis, I.; Papanikolaou, X.; Floyd, M.; Ji, K.H.; Kontoes, C.; Paradissis, D.; Zacharis, V. Mapping inflation at Santorini volcano, Greece, using GPS and InSAR. Geophys. Res. Lett. 2013, 40, 267–272. [Google Scholar] [CrossRef]
- Gudmundsson, S.; Sigmundsson, F.; Carstensen, J.M. Three-dimensional surface motion maps estimated from combined interferometric synthetic aperture radar and GPS data. J. Geophys. Res. Solid Earth 2002, 107, ETG 13-1–ETG 13-14. [Google Scholar] [CrossRef]
- Hu, X.; Lu, Z.; Pierson, T.C.; Kramer, R.; George, D.L. Combining InSAR and GPS to Determine Transient Movement and Thickness of a Seasonally Active Low-Gradient Translational Landslide. Geophys. Res. Lett. 2018, 45, 1453–1462. [Google Scholar] [CrossRef]
- Chang, W.L.; Smith, R.B.; Farrell, J.; Puskas, C.M. An extraordinary episode of Yellowstone caldera uplift, 2004–2010, from GPS and InSAR observations. Geophys. Res. Lett. 2010, 37, 6–11. [Google Scholar] [CrossRef] [Green Version]
- Johanson, I.A.; Bürgmann, R. Creep and quakes on the nothern transition zone of the San Andreas fault from GPS and InSAR data. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Gourmelen, N.; Amelung, F.; Lanari, R. Interferometric synthetic aperture radar-GPS integration: Interseismic strain accumulation across the Hunter Mountain fault in the eastern California shear zone. J. Geophys. Res. Solid Earth 2010, 115, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Manzo, M.; Ricciardi, G.P.; Casu, F.; Ventura, G.; Zeni, G.; Borgström, S.; Berardino, P.; Del Gaudio, C.; Lanari, R. Surface deformation analysis in the Ischia Island (Italy) based on spaceborne radar interferometry. J. Volcanol. Geotherm. Res. 2006, 151, 399–416. [Google Scholar] [CrossRef]
- Pritchard, M.E.; Simons, M.; Rosen, P.A.; Hensley, S.; Webb, F.H. Co-seismic slip from the 1995 July 30 Mw = 8.1 Antofagasta, Chile, earthquake as constrained by InSAR and GPS observations. Geophys. J. Int. 2002, 150, 362–376. [Google Scholar] [CrossRef] [Green Version]
- Xiong, L.; Xu, C.; Liu, Y.; Wen, Y.; Fang, J. 3D displacement field of wenchuan earthquake based on iterative least squares for virtual observation and GPS/inSAR observations. Remote Sens. 2020, 12, 977. [Google Scholar] [CrossRef]
- Delouis, B.; Giardini, D.; Lundgren, P.; Salichon, J. Joint inversion of InSAR, GPS, teleseismic, and strong-motion data for the spatial and temporal distribution of earthquake slip: Application to the 1999 İzmit mainshock. Bull. Seismol. Soc. Am. 2002, 92, 278–299. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.; Zheng, W.; Liu, Y.; Zhang, J.; Li, X. Integration of GPS with InSAR to monitoring of the Jiaju landslide in Sichuan, China. Landslides 2010, 7, 359–365. [Google Scholar] [CrossRef]
- Tong, X.; Sandwell, D.T.; Smith-Konter, B. High-resolution interseismic velocity data along the San Andreas Fault from GPS and InSAR. J. Geophys. Res. Solid Earth 2013, 118, 369–389. [Google Scholar] [CrossRef] [Green Version]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Fialko, Y.; Sandwell, D.; Simons, M.; Rosen, P. Three-dimensional deformation caused by the Bam, Iran, earthquake and the origin of shallow slip deficit. Nature 2005, 435, 295–299. [Google Scholar] [CrossRef]
- Ezquerro, P.; Del Soldato, M.; Solari, L.; Tomás, R.; Raspini, F.; Ceccatelli, M.; Fernández-Merodo, J.A.; Casagli, N.; Herrera, G. Vulnerability assessment of buildings due to land subsidence using insar data in the ancient historical city of pistoia (Italy). Sensors 2020, 20, 2749. [Google Scholar] [CrossRef] [PubMed]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw7.1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. 3D coseismic Displacement of 2010 Darfield, New Zealand earthquake estimated from multi-aperture InSAR and D-InSAR measurements. J. Geod. 2012, 86, 1029–1041. [Google Scholar] [CrossRef]
- Hu, J.; Ding, X.L.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Zhang, L. Kalman-Filter-Based Approach for Multisensor, Multitrack, and Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4226–4239. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving three-dimensional surface displacements from InSAR measurements: A review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Dai, K.; Liu, G.; Li, Z.; Li, T.; Yu, B.; Wang, X.; Singleton, A. Extracting vertical displacement rates in Shanghai (China) with multi-platform SAR images. Remote Sens. 2015, 7, 9542–9562. [Google Scholar] [CrossRef] [Green Version]
- Gray, L. Using multiple RADARSAT InSAR pairs to estimate a full three-dimensional solution for glacial ice movement. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Garthwaite, M.C. Resolving three-dimensional surface motion with InSAR: Constraints from multi-geometry data fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Zhang, X.; Liu, Z.; Zhu, Q. Spatiotemporal Characterization of Land Subsidence in Guandu (China) Revealed by Multisensor InSAR Observations. J. Sens. 2020, 2020, 8855364. [Google Scholar] [CrossRef]
- Samsonov, S.; d’Oreye, N. Multidimensional time-series analysis of ground deformation from multiple InSAR data sets applied to Virunga Volcanic Province. Geophys. J. Int. 2012, 191, 1095–1108. [Google Scholar] [CrossRef] [Green Version]
- Samsonov, S.V.; Tiampo, K.F.; Feng, W. Fast subsidence in downtown of Seattle observed with satellite radar. Remote Sens. Appl. Soc. Environ. 2016, 4, 179–187. [Google Scholar] [CrossRef]
- Pepe, A.; Solaro, G.; Calò, F.; Dema, C. A Minimum Acceleration Approach for the Retrieval of Multiplatform InSAR Deformation Time Series. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3883–3898. [Google Scholar] [CrossRef]
- Yu, L.; Yang, T.; Zhao, Q.; Liu, M.; Pepe, A. The 2015–2016 ground displacements of the Shanghai coastal area inferred from a combined COSMO-SkyMed/Sentinel-1 DInSAR analysis. Remote Sens. 2017, 9, 1194. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T.; Ueda, H. Advanced interferometric synthetic aperture radar (InSAR) time series analysis using interferograms of multiple-orbit tracks: A case study on Miyake-jima. J. Geophys. Res. Solid Earth 2011, 116, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ebmeier, S.K.; Biggs, J.; Mather, T.A.; Amelung, F. Applicability of InSAR to tropical volcanoes: Insights from Central America. Geol. Soc. Spec. Publ. 2013, 380, 15–37. [Google Scholar] [CrossRef] [Green Version]
- Werner, C.; Lowry, B.; Wegmuller, U.; Pugh, N.; Schrock, G.; Zhou, W. Deformation time-series derived from terrestrial radar observations using persistent scatterer interferometry in Seattle, Washington. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 6835–6838. [Google Scholar] [CrossRef]
- Monserrat, O.; Crosetto, M.; Cuevas, M.; Crippa, B. The thermal expansion component of persistent scatterer interferometry observations. IEEE Geosci. Remote Sens. Lett. 2011, 8, 864–868. [Google Scholar] [CrossRef]
- Wnuk, K.; Walton, G.; Zhou, W. Four-dimensional filtering of InSAR persistent scatterers elucidates subsidence induced by tunnel excavation in the Sri Lankan highlands. J. Appl. Remote Sens. 2019, 13, 034508. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.L.; Longuevergne, L.; Rivera, A. Assessing Groundwater Depletion and Dynamics Using GRACE and InSAR: Potential and Limitations. Groundwater 2016, 54, 768–780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donnellan, A.; Ludwig, L.G.; Parker, J.W.; Rundle, J.B.; Wang, J.; Pierce, M.; Blewitt, G.; Hensley, S. Potential for a large earthquake near Los Angeles inferred from the 2014 La Habra earthquake. Earth Space Sci. 2015, 2, 378–385. [Google Scholar] [CrossRef]
- Schaefer, L.N.; Lu, Z.; Oommen, T. Post-eruption deformation processes measured using ALOS-1 and UAVSAR InSAR at Pacaya Volcano, Guatemala. Remote Sens. 2016, 8, 73. [Google Scholar] [CrossRef] [Green Version]
- Schaefer, L.N.; Lu, Z.; Oommen, T. Dramatic volcanic instability revealed by InSAR. Geology 2015, 43, 743–746. [Google Scholar] [CrossRef] [Green Version]
- Wnuk, K.; Wauthier, C. Surface deformation induced by magmatic processes at Pacaya Volcano, Guatemala revealed by InSAR. J. Volcanol. Geotherm. Res. 2017, 344, 197–211. [Google Scholar] [CrossRef]
- Hu, X.; Bürgmann, R. Rheology of a Debris Slide From the Joint Analysis of UAVSAR and LiDAR Data. Geophys. Res. Lett. 2020, 47, 1–9. [Google Scholar] [CrossRef]
- Delbridge, B.G.; Bürgmann, R.; Fielding, E.; Hensley, S.; Schulz, W.H. Three-dimensional surface deformation derived from airborne interferometric UAVSAR: Application to the Slumgullion Landslide. J. Geophys. Res. Solid Earth 2016, 121, 3951–3977. [Google Scholar] [CrossRef] [Green Version]
- Hensley, S.; Wheeler, K.; Sadowy, G.; Jones, C.; Shaffer, S.; Zebker, H.; Miller, T.; Heavey, B.; Chuang, E.; Chao, R.; et al. The UAVSAR instrument: Description and first results. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Wheeler, K.; Sadowy, G.; Miller, T.; Shaffer, S.; Muellerschoen, R.; Jones, C.; Zebker, H.; Madsen, S. Uavsar: A new NASA airborne SAR system for science and technology research. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006. [Google Scholar]
- Hensley, S.; Zebker, H.; Jones, C.; Michel, T.; Muellerschoen, R.; Chapman, B. First deformation results using the NASA/JPL UAVSAR instrument. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 26–30 October 2009. [Google Scholar]
- Baker, G. Regional Connector Transit Project Quarterly Project Status Report, March 2020. Available online: https://media.metro.net/2020/March-2020-Regional-Connector-QPSR.pdf (accessed on 15 October 2020).
- Zheng, H.; Bragard, C.; Calvo, C.H.; Mooney, M.; Gutierrez, M. Observed Performance and Analysis of SEM Cavern Construction in Downtown Los Angeles. J. Geotech. Geoenvironmental Eng. 2021, 147, 05021011. [Google Scholar] [CrossRef]
- Khorrami, M.; Alizadeh, B.; Tousi, E.G.; Shakerian, M.; Maghsoudi, Y.; Rahgozar, P. How groundwater level fluctuations and geotechnical properties lead to asymmetric subsidence: A PSInSAR analysis of land deformation over a transit corridor in the Los Angeles metropolitan area. Remote Sens. 2019, 11, 377. [Google Scholar] [CrossRef] [Green Version]
- Blewitt, G.; Hammond, W.; Kreemer, C. Harnessing the GPS Data Explosion for Interdisciplinary Science. Eos 2018, 99, 485. [Google Scholar] [CrossRef]
- Hudnut, K.; King, N.; Aspiotes, A.G.; Borsa, A.A.; Determan, D.N.; Galetzka, J.E.; Stark, K.F. SCIGN USGS GPS Network—MTA1-Civic Center MTA P.S., The GAGE Facility operated by UNAVCO, Inc., GPS/GNSS Observations Dataset. 2006. Available online: https://doi.org/10.7283/T53X84XV (accessed on 24 October 2021).
- Wegmüller, U.; Werner, C. Mitigation of thermal expansion phase in persistent scatterer interferometry in an urban environment. In Proceedings of the 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015. [Google Scholar]
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and interferometric processing software. In Proceedings of the ERS-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2000; pp. 211–219. [Google Scholar]
- Wegnüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A.; Frey, O.; Santoro, M. Sentinel-1 Support in the GAMMA Software. Procedia Comput. Sci. 2016, 100, 1305–1312. [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, A.N.; Arsenin, V.Y. Solution of Ill-Posed Problems; Winston/Wiley: Washington, DC, USA, 1977. [Google Scholar]
- Hansen, P.C.; O’leary, D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Rezghi, M.; Hosseini, S.M. A new variant of L-curve for Tikhonov regularization. J. Comput. Appl. Math. 2009, 231, 914–924. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.C. REGULARIZATION TOOLS: A Matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 1994, 6, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Terzaghi, K. Principles of soil mechanics, IV—Settlement and consolidation of clay. Eng. News Record 1925, 95, 874–878. [Google Scholar]
- Meldebekova, G.; Yu, C.; Li, Z. Quantifying Ground Subsidence Associated with Aquifer Overexploitation Using Space-Borne Radar Interferometry in Kabul, Afghanistan. Remote Sens. 2020, 12, 2461. [Google Scholar] [CrossRef]
- Wanwan, Z.; Yinghai, K.; Huili, G.; Lin, Z.; Beibei, C. Monitoring of land surface deformation in Beijing with time-series InSAR technique based on multi-band InSAR data using RADARSAT-2 and TERRASAR-X. In Proceedings of the 2016 4th International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Guangzhou, China, 4–6 July 2016. [Google Scholar]
- Chaussard, E.; Amelung, F.; Abidin, H.; Hong, S.H. Sinking cities in Indonesia: ALOS PALSAR detects rapid subsidence due to groundwater and gas extraction. Remote Sens. Environ. 2013, 128, 150–161. [Google Scholar] [CrossRef]
- Bonì, R.; Herrera, G.; Meisina, C.; Notti, D.; Béjar-Pizarro, M.; Zucca, F.; González, P.J.; Palano, M.; Tomás, R.; Fernández, J.; et al. Twenty-year advanced DInSAR analysis of severe land subsidence: The Alto Guadalentín Basin (Spain) case study. Eng. Geol. 2015, 198, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Chaussard, E.; Wdowinski, S.; Cabral-Cano, E.; Amelung, F. Land subsidence in central Mexico detected by ALOS InSAR time-series. Remote Sens. Environ. 2014, 140, 94–106. [Google Scholar] [CrossRef]
- Chilingarian, G.V.; Knight, L. Relationship Between Pressure and Moisture Content of Kaolinite, Illite, and Montmorillonite Clays. Am. Assoc. Pet. Geol. Bull. 1960, 44, 101–106. [Google Scholar]
- Chen, C.T.; Hu, J.C.; Lu, C.Y.; Lee, J.C.; Chan, Y.C. Thirty-year land elevation change from subsidence to uplift following the termination of groundwater pumping and its geological implications in the Metropolitan Taipei Basin, Northern Taiwan. Eng. Geol. 2007, 95, 30–47. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Myer, D.; Mellors, R.; Shimada, M.; Brooks, B.; Foster, J. Accuracy and resolution of ALOS interferometry: Vector deformation maps of the father’s day intrusion at Kilauea. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3524–3534. [Google Scholar] [CrossRef] [Green Version]
- Goel, K.; Gonzalez, F.R.; Adam, N.; Duro, J.; Gaset, M. Thermal dilation monitoring of complex urban infrastructure using high resolution SAR data. In Proceedings of the International Symposium on Geoscience and Remote Sensing (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 954–957. [Google Scholar]
- Lowry, B.W.; Baker, S.; Zhou, W. A case study of novel landslide activity recognition using ALOS-1 InSAR within the ragged mountain Western Hillslope in Gunnison county, Colorado, USA. Remote Sens. 2020, 12, 1969. [Google Scholar] [CrossRef]
- Lowry, B.; Gomez, F.; Zhou, W.; Mooney, M.A.; Held, B.; Grasmick, J. High resolution displacement monitoring of a slow velocity landslide using ground based radar interferometry. Eng. Geol. 2013, 166, 160–169. [Google Scholar] [CrossRef]
- Hu, X.; Bürgmann, R.; Schulz, W.H.; Fielding, E.J. Four-dimensional surface motions of the Slumgullion landslide and quantification of hydrometeorological forcing. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]











| Sensor | Path | LOS Azimuth (φ) | Radar Incidence Angle (ϑ) | Spatial Resolution (m) | Time Span | Number of Acquisitions | Maximum Baseline (m) | PS Density (PS/km2) |
|---|---|---|---|---|---|---|---|---|
| Sentinel-1 | 137 | 77° | 44° | 2.3 × 14.1 | 9 January 2018–3 July 2019 | 66 | 163 | 2550 |
| Sentinel-1 | 71 | 283° | 39° | 2.3 × 14.1 | 10 January 2018–22 June 2019 | 45 | 126 | 3164 |
| Sentinel-1 | 64 | 77° | 34° | 2.3 × 14.1 | 4 January 2018–28 June 2019 | 40 | 116 | 2240 |
| COSMO- | - | 279° | 53° | 1.7 × 2.0 | 12 January 2018–5 July 2019 | 25 | 758 | 8028 |
| SkyMed | ||||||||
| UAVSAR | 08523 | 356° | 55° | 1.7 × 0.6 | 23 April 2009–21 February 2019 | 15 | N/A | 41,086 |
| UAVSAR | 26524 | 174° | 52° | 1.7 × 0.6 | 23 April 2009–21 February 2019 | 18 | N/A | 38,124 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wnuk, K.; Zhou, W.; Gutierrez, M. Mapping Urban Excavation Induced Deformation in 3D via Multiplatform InSAR Time-Series. Remote Sens. 2021, 13, 4748. https://doi.org/10.3390/rs13234748
Wnuk K, Zhou W, Gutierrez M. Mapping Urban Excavation Induced Deformation in 3D via Multiplatform InSAR Time-Series. Remote Sensing. 2021; 13(23):4748. https://doi.org/10.3390/rs13234748
Chicago/Turabian StyleWnuk, Kendall, Wendy Zhou, and Marte Gutierrez. 2021. "Mapping Urban Excavation Induced Deformation in 3D via Multiplatform InSAR Time-Series" Remote Sensing 13, no. 23: 4748. https://doi.org/10.3390/rs13234748
APA StyleWnuk, K., Zhou, W., & Gutierrez, M. (2021). Mapping Urban Excavation Induced Deformation in 3D via Multiplatform InSAR Time-Series. Remote Sensing, 13(23), 4748. https://doi.org/10.3390/rs13234748