Long-Term Gully Erosion and Its Response to Human Intervention in the Tableland Region of the Chinese Loess Plateau

Abstract

The gully erosion process is influenced by both natural conditions and human activities on the tableland region, the Chinese Loess Plateau, which is a densely populated agricultural area with unique topography. For the purpose of assessing long-term gully growth rates, the influencing factors and potential of gully growth, KH-4B satellite images, Quickbird-2 images, and unmanned aerial vehicle (UAV) images were used to assess gully erosion from 1969 to 2019. The effects of runoff, topography and human activities were analyzed with information derived from historical and present images. Ninety-five investigated gullies were classified into four types: 45 growing, 25 stable, 21 infilled and four excavated gullies. The rates (R_A) of 45 growing gullies ranged from 0.50 to 20.94 m²·yr⁻¹, with an average of 5.66 m²·yr⁻¹ from 1969 to 2010. The present drainage area, local slope, average drainage slope, annual runoff, and ratio of the terraced area were all significantly different between the stable and growing gullies. The long-term gully growth rate could be estimated using a nonlinear regression model with annual runoff (Q_a) and the slope of the drainage area (S_d) as predictors (R_A = 0.301Q_a^0.562 S_d, R² = 0.530). Based on the S_g-A and S_g-Q_a relationship that was used to reveal the threshold conditions for gully growth, all growing gullies still have the potential to keep growing, but soil and water conservation measures, including terraces, could change the threshold condition by reducing the effective drainage area. The results of this study could be helpful for preventing further gully erosion by dealing with gullies far above the threshold line.

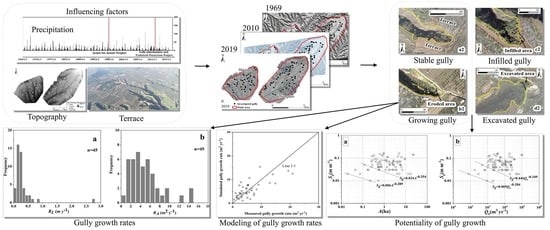
1. Introduction

Gully erosion is the process whereby water accumulates and often recurs in narrow channels and, over short periods, removes the soil from this narrow area to considerable depths, as defined by the Soil Science Society of America (https://www.soils.org/publications/soils-glossary/#, accessed on 1 October 2021). Gully erosion represents a minimum of 10% to a maximum of 94% of the total sediment yield caused by water erosion [1], which is a major driver of land degradation on the global scale [2,3,4,5]. To control gully erosion, understanding gully head initiation and growth is necessary [1,2,3,4,6,7]. Gullies were developed only when the intensity of concentrated (overland) water flows during a rain event exceeded the threshold [1]. However, flow hydraulics for gully initiation are constrained in field measurements [1,3]. The critical environmental conditions of gullies were assessed in terms of precipitation [8], topography [7,9], soils and land use [10,11]. These factors control either the runoff hydraulics (e.g., precipitation, topography) or the resistance of the soil surface to incision (e.g., soils) or both (e.g., land use) [1].

Frankl et al. [12] found that the average headcut growth rate during the 2010 rainy season was 0.34 m·yr⁻¹, compared with 3.8 m·yr⁻¹ during medium to long time periods (1–47 years) in northern Ethiopia. Vandekerckhove et al. [13] found that gully headcut growth rates varied from 0.00 to 0.86 m·yr⁻¹ during the medium term (21–38 years) in Southeast Spain. Ionita et al. [14] found that the mean gully head retreat rate of 14 gullies was 7.7 m·yr⁻¹ during 1961–2020 on the Moldavian Plateau of Romania. However, Nicu [15] investigated the gully erosion rate of three typical gullies also on the Moldavian Plateau from 1976 to 2013 and found that the average rate was approximately 0.1–0.15 m·yr⁻¹. These studies show that gully growth rates vary greatly under different conditions. Vanmaercke et al. [4,5] pointed out that gully head growth rates can be subject to very large temporal variabilities. Nevertheless, understanding gully growth over a long-term period is essential, especially when addressing the consequences of future land use and climate change scenarios [1,2,16].

It is difficult to detect long-term gully growth rates in many regions because of the unavailability of historical data. Satellite and airborne images have been widely used for measuring gully head retreats over medium- to long-term time scales [13,17,18,19,20,21,22]. Good estimations of gully retreat by remote sensing require a high spatial resolution of the images [13]. Recently, widespread unmanned aerial vehicles (UAVs) have become flexible and cost-efficient for acquiring gully statuses. Simultaneous advances in computer vision and digital photogrammetry, which enable the fast and facile generation of digital surface models (DSMs) with high resolution and accuracy [23,24,25], have boosted the establishment of UAVs as a suitable field survey method. Several previous studies already adopted DSMs with as high as cm-accurate resolution calculated from UAV images for volume estimations, erosion rate measurements, morphological analyses and monitoring of gully growth [8,17,22,25,26]. Therefore, a good way to detect long-term and large-scale gully growth rates is to compare historical satellite images with present UAV images.

On the Chinese Loess Plateau, severe soil erosion has carved hundreds of thousands of gullies in the landscape [27], and gully erosion is an important soil erosion process, contributing 60~90% of the total sediment production in agricultural areas [28,29]. The hilly gully region, which is the main part of the Loess Plateau, has received wide attention with respect to gully erosion and its controlling factors in previous studies [30,31,32]. However, the tableland region, which covers approximately 2 × 10⁵ km², is the most important agricultural region on the Loess Plateau [33]. The tableland region is characterized by broad and flat top surfaces (average slope gradient < 0.09 m·m⁻¹) threatened by surrounding deep gully systems (Figure 1). Gully erosion induced by concentrated flow generated from the loess tableland top flat surface is the main source of sediment yield in the tableland region [34], and many soil conservation measures have been put into practice, such as water barriers along gully boundaries and terraces on the sloping cropland to control gully erosion around the tableland, check dams to stabilize the channel since the 2010’s. In Romania, these measures, like check dams [14] are also used to control gully erosion. However, the understanding of gully head growth in the loess tableland region, especially in the long term, has been limited in previous studies. The unique topography of the tableland region and the dense population have led to differences in hydrologic conditions (e.g., runoff discharge and velocity) and hydrological connectivity as well as human intervention from other regions, which may influence gully erosion processes [35,36,37]. Therefore, investigation of the long-term gully erosion dynamics in such areas is of great significance for broadening the knowledge of gully erosion and its relationships with human activities.

This study aimed to examine the changes in gullies over a time scale of 50 years under the influence of intense human activities in the tableland region of the Loess Plateau. The specific objectives of this study were to (1) estimate gully head growth rates and the main factors influencing these growth rates from 1969 to 2019, (2) build a regression model of gully growth rates for gullies with little human intervention, and (3) determine the topographic thresholds and potentials of gully growth in the tableland region on the Loess Plateau.

2. Materials and Methods

2.1. Study Area

The Zhongduo tableland (110.67–110.75°E, 35.97–36.04°N; 32 km²) and the Shiquan tableland (110.60–110.66°E, 35.97–36.03°N; 20 km²) on the southeastern Loess Plateau were selected as study areas; they are located in Jixian County, Shanxi Province, China (Figure 1). The loess cover is approximately 150 m thick, and the main soil type is loessial carbonate cinnamon soil with weak alkalinity in the study area. There is a typical temperate continental monsoon climate with an average annual precipitation of 507.47 mm and an average annual erosive precipitation (precipitation > 12 mm·d⁻¹) of 314.71 mm (1957–2019) (based on meteorological records from the China Meteorological Data Service Centre [CMDC], http://data.cma.cn/, accessed on 9 August 2020). Approximately 70% of precipitation events occur from June to September. People mainly live on the flat surface of the tableland, which has agricultural advantages. Most of the tableland area was reclaimed as farmland in the study area. Before the implementation of the Grain for Green Project (GFGP) in 2000, the main land use types were croplands for growing wheat (Triticum aestivum), corn (Zea mays), soybeans (Glycine max), and flue-cured tobacco (Nicotiana tabacum). Since 2000, most of the croplands have been converted into apple orchards for both economic benefits and mitigating soil erosion. The valley area is dominated by forestland and shrubland due to natural vegetation restoration. The Gully Stabilization and Tableland Protection Project (GSTP) was launched in the 2010s to stabilize the channel and control gully erosion around the tableland, which includes water barriers, terraces, check dams, etc.

2.2. Base Data Collection and Gully Sampling

KH-4B satellite images, Quickbird-2 satellite images and UAV images were used to acquire information about topography, land use and land cover in 1969, 2010 and 2019, respectively (

Table 1. Information for the images used in this study.

Platform	Photo Date	Ground Sampling Distance (GSD)	Number of Bands 2
KH-4B	13/12/1969	3.10 m	1 (photographic film)
Quickbird-2	12/12/2010	0.61 m 1	4 (MUL) + 1 (PAN)
DJI Inspire 2	17/10–19/10/2019	0.14 m	3 (MUL)

¹. The panchromatic and multispectral bands were fused to create a 0.61 m pansharpened image using ENVI 5.3 software. ². PAN indicates a panchromatic band; MUL indicates multispectral bands.

). KH-4B (where KH is Key Hole), a space reconnaissance satellite launched during the cold war era, offered the best ground resolution of approximately 1.8 m [38]. During the operational phase, panchromatic images of large areas of the world were recorded on film. These satellite images were declassified in 1995 and have been available to the public since then and are used for environmental and resource research [38,39] (KH-4B images can be downloaded from the U.S. Geological Survey website, https://earthexplorer.usgs.gov/, accessed on 19 May 2020). The Quickbird-2 images contained four multispectral bands (MULs) with a 2.44 m spatial resolution and one panchromatic band (PAN) with a 0.61 m spatial resolution, which were fused to create a 0.61 m pansharpened image after the images were preprocessed (Table 1). UAV images were acquired in 2019 with a 0.14 m ground sampling distance (GSD) with a flying height of 500 m. Pix4Dmapper 4.4.12 software was used to automatically mosaic and process UAV images, to generate digital orthograph models (DOMs) and digital elevation models (DEMs) with a spatial resolution of 0.14 m. KH-4B and Quickbird-2 images were georeferenced to UAV images with a set of ground control points (GCPs) visible in all three image phases.

Gullies along the tableland boundary were investigated by even sampling, but the selected gullies needed to be easy to identify in the 1969, 2010, and 2019 images. The gully edges were interpreted visually from the KH-4B, Quickbird-2, and UAV images, and linear and areal gully growth rates (R_L, m·yr⁻¹ and R_A, m²·yr⁻¹) were calculated. The present drainage area (A, m²) of each investigated gully head, slope gradient at the gully head (S_g, m·m⁻¹), and average slope of the drainage area (S_d, m·m⁻¹) were extracted based on the DEMs generated from the UAV images. The land use types, including cropland, apple orchards, forestland, shrubland, grassland, bare land, fallow fields, paved roads, unpaved roads and construction sites as well as terraces in the drainage area in 1969, 2010, and 2019 were interpreted visually based on those images. All map layers were georeferenced to the UTM Zone 49N coordinate system.

Precipitation data from 1969 to 2019 were obtained from the CMDC (Figure 2). The precipitation records were divided into three periods (1969–1999, 2000–2014, and 2015–2019), representing records before the GFGP, after the GFGP, and after the GSTP. To explore the relationship between gully growth rates and precipitation characteristics, precipitation parameters were calculated, i.e., average annual precipitation, average annual erosive precipitation (>12 mm·d⁻¹) [40], rainfall amount in storm events (>50 mm·d⁻¹), and rainfall amount in heavy rainstorm events (>100 mm·d⁻¹) [41].

2.3. Topographic and Hydraulic Parameter Calculation and Data Analysis

The stream power index (SPI) is a parameter related to surface and subsurface runoff transport processes [42] and has been widely used in gully erosion susceptibility research [43,44,45,46]. The SPI at the gully head was calculated as follows:

SPI = A^0.5S_d

(1)

where A is the present drainage area (m²) and S_d is the average slope in the drainage area (m·m⁻¹).

The runoff onto one gully head (Q_gh, m³) from the drainage area with certain land use scenarios was calculated as follows:

$$Q_{gh}=\frac{{\sum }_{i=1}^n{Q}_i{A}_i}{1000}$$

(2)

where Q_i is the runoff depth (mm) of land use type i, A_i is the area (m²) of land use type i in the drainage area of each gully head, and n is the number of land use types in the drainage area of each gully head.

The NRC runoff curve number method (CN method, USDA-National Engineering Handbook, Part 630, Chapter 10, www.nrcs.usda.gov/wps/portal/nrcs/detailfull/national/water/manage/hydrology, accessed on 13 January 2021) was used to estimate the event runoff of land use type i onto the gully head from the drainage area (Q_i), which takes the impact of land use and precipitation into account [5,47,48].

$$Q_i=\frac{{(P-\lambda S_i)}^2}{P+(1-\lambda )S_i}$$

(3)

$$S_i=\frac{25,400}{C{N}_i}-254$$

(4)

where P is rainfall (mm), S_i is the maximum potential loss to runoff for land use type i (mm), λ is the fraction of S representing the initial abstraction coefficient (λ is 0.2 in this paper), and CN_i is the curve number of land use type i. Key impact factors of the curve number (CN) include soil properties, land use type, slope, antecedent moisture conditions, vegetation coverage, and land management practices [49,50]. Different land uses were assigned to different CN values (

Table 2. CN values used to estimate runoff from the drainage area of each gully head.

Land Use Type	Curve Number (CN) 1
Apple orchard (crown density < 20%)	79.6
Apple orchard (20% < crown density < 60%)	78.8
Apple orchard (crown density > 60%)	78.5
Cropland (vegetation coverage < 20%)	79.6
Cropland (20% < vegetation coverage < 60%)	77.3
Cropland (vegetation coverage > 60%)	75.6
Forestland	78.5
Shrub land	78.1
Grassland	77
Fallow field	77.8
Bare land	79.6
Construction land	100 2
Unpaved road	79.6 3

¹. The CN values were calculated according to Feng et al. [51] based on observed data from runoff plots on the Chinese Loess Plateau; CN values are reduced by 11.1% when land use types have terraces [51]. ². Construction land consists of village buildings and paved roads that usually have little or no infiltration; therefore, the CN value is 100. ³. The CN values of the roads were determined according to the bare land.

) based on previous research on similar land uses on the Loess Plateau [51].

Runoff in 3 periods (1969–1999, 2000–2014, and 2015–2019) generated by annual average total precipitation (P_a69, P_a10, and P_a19), erosive precipitation (P_ae69, P_ae10, and P_ae19), accumulated rainfall in rainstorm events (P_r69, P_r10, and P_r19), and accumulated rainfall in heavy rainstorm events (P_hr69, P_hr10, and P_hr19) were calculated via Equation (3) and corresponding land use scenarios (1969, 2010, and 2019) as follows:

$$Q_a=\frac{{31Q}_{a69}{+15Q}_{a10}{+5Q}_{a19}}{51}; Q_{a6910}=\frac{{31Q}_{a69}{+10Q}_{a10}}{41}$$

(5)

$$Q_{ae}=\frac{{31Q}_{ae69}{+15Q}_{ae10}{+5Q}_{ae19}}{51}; Q_{ae6910}=\frac{{31Q}_{ae69}{+10Q}_{ae10}}{41}$$

(6)

$$Q_r{=25Q}_{r69}{+13Q}_{r10}{+Q}_{r19}; Q_{r6910}{=25Q}_{r69}{+13Q}_{r10}$$

(7)

$$Q_{hr}{=Q}_{hr69}{+Q}_{hr10}$$

(8)

where Q_a (m³·yr⁻¹) and Q_ae (m³·yr⁻¹) are the annual average runoff in 51 years from 1969 to 2019 caused by total precipitation and erosive precipitation, respectively; Q_r (m³) and Q_hr (m³) are the accumulated runoff generated by rainstorms (39 events) and heavy rainstorms (2 events), respectively, from 1969 to 2019. The same method can be used to calculate the annual average runoff (Q_a6910 and Q_ae6910, m³·yr⁻¹) and accumulated runoff (Q_r6910, m³) generated by rainstorms (38 events) from 1969 to 2010.

2.4. Statistical Analysis and Assessment Methods

Classical statistics, such as measures of center, variation and shape, were used to assess the change of gully dimensions. The Mann–Whitney test and Pearson chi-square test (χ²) were used to compare the differences in A, S_d, S_g, and Q_gh between the 2 types of gullies (growing and stable). Pearson correlation coefficients (r) were used to evaluate the relationships of A, S_d, S_g, and Q_gh to the gully head growth rates. Nonlinear regression was used to fit models for the gully growth rates. The coefficient of determination (R²) and significant level of F test were used to evaluate the performance of the regression models. SPSS 24 software was used for statistical calculation and model parameter calibration.

3. Results

3.1. Gully Growth from 1969 to 2019

According to changes in the gully edges from 1969 to 2019, 95 investigated gullies were classified into four types: stable, growing, infilled, and excavated (Figure 3). Twenty-five gullies were classified as stable and had no obvious changes between the 1969 and 2019 images. Infilled and excavated gullies showed obvious gully area changes caused by human activities. Twenty-one gullies were infilled with a decrease in gully area ranging from 30.22 to 708.17 m², with an average of 257.15 m². These infilled gullies enlarged the tableland area and prevented further gully headcuts locally. Four gullies were excavated with increases in gully areas of 71.74, 185.41, 244.16, and 355.16 m². Two of the four excavated gullies were excavated for cave dwellings, and another two gullies were cut on slopes to prevent landslides. The average present drainage area, local slope, and average annual linear/areal gully growth rate of the four types of gullies are listed in

Table 3. Information of investigated gullies.

Gully Type	Sample Size	Number of Gullies with Terraces 1			A (ha)	Sg (m·m−1)	RL2 (m·yr−1)			RA (m2·yr−1)
		1969	2010	2019			Min	Max	Average	Min	Max	Average
Growing	45	8	27	35	2.96	0.07	0.04	2.78	0.30	0.50	20.94	5.66
Stable	25	14	22	24	2.08	0.05	-	-	-	-	-	-
Infilled	21	0	14	16	3.08	0.05	-	-	-	−0.60	−14.16	−5.14
Excavated	4	0	3	4	9.30	0.06	-	-	-	1.43	7.10	4.28

A—Average present drainage area; S_g—average slope gradient near the gully head; R_L—linear gully growth rate; R_A—areal gully growth rate. ¹. Number of gullies with terraces in drainage areas in 1969, 2010, and 2019. ². The R_L and R_A values of the growing gullies were from 1969 to 2010; the R_L and R_A values of the infilled and excavated gullies were from 1969 to 2019.

. Among the 95 investigated gullies, 51 gullies were located on the Zhongduo tableland, and 44 gullies were located on the Shiquan tableland (Figure 4).

Forty-five gullies developed from 1969 to 2010. However, 26 of the 45 growing gullies were stable, and 2 of the 45 gullies were infilled during 2010–2019. Only 17 gullies kept growing from 2010 to 2019. The R_L values from 1969 to 2010 of the 45 growing gullies ranged from 0.04 to 2.78 m·yr⁻¹, with an average of 0.30 m·yr⁻¹, and the R_L values of 34 gullies were less than 0.30 m·yr⁻¹. The highest R_L value was 2.78 m·yr⁻¹, which was probably due to the unpaved road on the gully head as a concentrated channel for runoff leading to gully growth (Figure 5a). The R_A values from 1969 to 2010 of the 45 growing gullies ranged from 0.50 to 20.94 m²·yr⁻¹, with an average of 5.66 m²·yr⁻¹. Fifty percent of the R_A values ranged from 2.64 to 6.72 m²·yr⁻¹ (Figure 5b).

3.2. Influencing Factors of and Modeling of Gully Growth Rates

Infilled and excavated gullies were controlled by human activity; therefore, they were not taken into consideration for further analysis of the factors that influence gully growth rates.

Gullies without obvious human intervention were analyzed to determine the influencing factors from the aspects of topography and hydraulics. The Mann–Whitney test indicated that the differences in four influencing factors (A, S_g, S_d, and Q_gh) between growing gullies and stable gullies were statistically significant (p < 0.05). The average A values of growing and stable gullies were 2.96 ha and 2.08 ha, respectively. The average S_g values of the growing and stable gully heads were 0.07 m·m⁻¹ and 0.05 m·m⁻¹, respectively. The average S_d values of the growing and stable gully heads were 0.11 m·m⁻¹ and 0.16 m·m⁻¹, respectively. The Q_a values of the growing and stable gully heads were 12942.49 m³·yr⁻¹ and 8351.19 m³·yr⁻¹, respectively. The Pearson chi-square test indicated that gullies were growing or stable and depended significantly on the presence/absence of terraces in 1969 (χ² = 14.731, p < 0.001). Among the 25 stable gullies from 1969 to 2019, 15 were drained areas with terraces since 1969, while among the 45 growing gullies, 7 were drained areas with terraces since 1969. This result showed that terraces, as an effective soil and water conservation measure, had strong effects on gully growth in the past 50 years in the tableland region.

Pearson’s correlation tests were used to examine the relationship between 45 growing gullies and their influencing factors. No significant correlations were found between S_d or S_g and gully growth rates from 1969 to 2010, while A, Q_a6910, Q_ae6910, Q_r6910, and Q_hr correlated significantly with the gully head growth rates from 1969 to 2010 (

Table 4. Pearson’s correlation coefficients (r) of the gully growth rate and influencing factors.

	RL	RA	A	Sg	Sd	Qa6910	Qae6910	Qr6910	Qhr	SPI
RL	1	0.504 **	0.132	−0.148	0.038	0.416 **	0.416 **	0.259	0.330 *	0.174
RA		1	0.426 **	−0.104	0.061	0.533 **	0.526 **	0.366 *	0.457 **	0.640 **

R_L—Linear gully growth rate from 1969 to 2010 in m·yr⁻¹; R_A—areal gully growth rate from 1969 to 2010 in m²·yr⁻¹; A—present drainage area in m²; S_g—local slope gradients near the gully head in m·m⁻¹; S_d—slope gradients of the drainage area in m·m⁻¹; Q_a6910 and Q_ae6910—annual average runoff in 41 years from 1969 to 2010 calculated with total precipitation and erosive precipitation, respectively, in m³·yr⁻¹; Q_r6910 and Q_hr—accumulated runoff generated by rainstorms (38 events) and heavy rainstorms (2 events), respectively, in m³. SPI—stream power index. ** Correlation is significant at the 0.01 level. * Correlation is significant at the 0.05 level.

). Compared to the relationship between R_L and its influencing factors, larger correlation coefficients were found between R_A and its factors. The correlation coefficients between R_A and Q_a6910, Q_ae6910, and Q_hr were larger than those between R_A and A. These results indicate that gully growth rates were significantly influenced by runoff.

Nonlinear regression models for the gully growth rate from 1969 to 2010 were fitted, as summarized in

Table 5. Summary of the models of gully growth rates from 1969 to 2010 (n = 45).

Parameter	Model Equation	R2	Equation No.
A	RA = 4.317A0.4369	0.273	(9)
SPI	RA = 0.302SPI1.060	0.411	(10)
Qa6910	RA = 0.117Qa69100.422	0.364	(11)
Qa6910, Sd	RA = 0.301Qa69100.562 Sd	0.530	(12)

A—Present drainage area in ha; SPI-stream power index calculated by Equation (1); Q_a6910—estimated average annual runoff from 1960 to 2010 in m³·yr⁻¹; S_d—average slope of the drainage area in m·m⁻¹; R_A—areal gully retreat rate from 1969 to 2010 in m²·yr⁻¹.

. Drainage areas were widely used as surrogates for surface or subsurface runoff in previous studies of gully erosion [52], but the low R² indicated that they did not work well in this study. Compounding the average annual runoff (Q_a6910) and average slope of the drainage area (S_d) presented a better performance in modeling the gully growth rate, as shown in Equation (12) in Table 5. The measured R_A of each gully and the corresponding R_A simulated by Equation (12) is plotted in Figure 6, suggesting the good performance of Equation (12).

3.3. Threshold Conditions of Gully Head Growth

The topographic slope-area (S_g-A) relationship has been widely used to understand the threshold conditions for gully initiation and development [7,52] and is commonly expressed in critical S_g-A relationships, i.e., S_g = kA^−b. The S_g-A relationship of stable gullies was fitted with the lowermost data points with S_g = 0.006^−0.289, and the threshold condition for growing gullies was S_g = 0.024A^−0.354 (Figure 7a). The present drainage area (A) of 45 growing gullies ranged from 0.25 to 22.44 ha, with an average of 2.96 ha, and the S_g values ranged from 0.02 to 0.16 m·m⁻¹, with an average of 0.07 m·m⁻¹. The A values of 25 stable gullies ranged from 0.02 to 17.2 ha, with an average of 2.08 ha, and the S_g values ranged from 0.01 to 0.13 m·m⁻¹, with an average S_g of 0.05 m·m⁻¹. Both the average A and average S_g of growing gullies were larger than those of stable gullies, and the k values of growing gullies were much larger than the k values of stable gullies, indicating that growing gullies have the potential to keep growing (Figure 7a).

On the other hand, Figure 7a shows that 17 stable gullies were above the line S_g = 0.024 A^−0.354, among which 10 gullies developed terraces in their drainage area since 1969, indicating that the terraces could change the threshold condition by reducing the effective drainage area. Then, the critical relationship S_g-Q_a can reveal the threshold conditions for gully growth better than the S_g-Q_a relationship because gully erosion is driven mainly by accumulated runoff, which is usually substituted with drainage area (Figure 7b). Critical conditions for stable and growing gullies were S_g = 0.483Q_a^−0.359 and S_g = 0.070Q_a^−0.286, respectively. The minimum annual average runoff onto the investigated growing gullies was approximately 1000 m³·yr⁻¹, compared with 80 m³·yr⁻¹ for the investigated stable gullies. Among 45 growing gullies, 17 gullies that still grew from 2010 to 2019 are marked as gray dots in Figure 7.

4. Discussion

4.1. Long-Term Gully Growth Rates in the Tableland of the Loess Plateau

Gully growth rates in different studies are listed in

Table 6. Gully growth rates in different parts of the Loess Plateau in published papers and this study.

No.	Region and Location	Average RL (m·yr−1)	Average RA (m2·yr−1)	Land Use Types	Average Pa (mm)	MP (yr.)	Number of Samples	Reference
1	Tableland region on the southeastern Loess Plateau	0.30	5.66	Orchard, cropland	500.48 (1969–2010)	40	45	This study
2	Hilly gully region on the northeastern Loess Plateau	0.54	9.1	Cropland	397 (1959–2018)	59	30	[22]
3	Hilly gully region on the central Loess Plateau	0.49	-	Cropland, grassland	520.54 (1976–1997)	21	138	[58]
4	The Moldavian Plateau of Romania	0.61	-	Deforestation	500–700	65	1	[59]

R_L—Linear gully growth rate; R_A—areal gully growth rate; P_a—annual precipitation; MP—monitoring period.

. Compared with the hilly gully region in the medium- or long-term, the average R_L (0.30 m·yr⁻¹) in the tableland region in this study was lower. The first reason may be the much smaller slope gradients of the drainage area on the tableland than in the hilly gully region. When the hydraulic radius is constant, the shear stress of the shallow flow is proportional to the slope gradient [53]; therefore, gentler slopes may produce a smaller shear stress of the shallow flow. At the same time, the slope gradient is related to hydrological connectivity [35,36,37]. Hydrological connectivity can be quantitatively described by topographic parameters, including the slope gradient and upslope area [54], so that gentler slopes may result in lower hydrological connectivity. In addition, soil and water conservation measures are very common in the study area and have an effect on hydrological connectivity. The tableland boundary was ridged with a shrub belt, and small reservoirs in the drainage area could reduce direct runoff into gullies. Terraces can also lead to a further decrease in hydrological connectivity [36,55]. The hydrological connectivity of the drainage area on the tableland should be lower than that in the hilly gully region owing to the gentler slope, soil and water conservation measures, and piping erosion in the drainage area. Lower hydrological connectivity may be the main reason for the lower gully growth rates in the tableland region. The average R_L (0.30 m·yr⁻¹) in this study was also lower (Table 6) than the gully growth rate in the Moldavian Plateau of Romania, where the topographical characters are similar to the hilly gully region of the Loess Plateau and the higher R_L could be owed to the massive deforestation in 1990. Although the gully growth rates in the tableland regions were relatively low, unpaved roads with high erodibility, as the key components of hydrological connectivity [36], could lead to gully growth [56,57]. An unpaved road to the gully head may be the main reason for the largest erosion rate. Thus, soil and water conservation measures should focus on unpaved roads in tableland regions in the future.

Runoff is the main driver of gully headcuts because gully heads can only develop if concentrated (overland) flow intensity during a rain event exceeds a threshold value [1]. However, measuring critical flow hydraulics (e.g., runoff discharge and velocity) for gully erosion is constrained under field conditions [1,3,5]. The CN method provides an approach to estimate direct runoff in a certain land use type [47,48,49]. Likewise, combining a pixel-based CN approach with flow-routing algorithms makes it possible to account for the effect of the spatial patterns of topography, soil conditions and land cover [5]. Resent research has also found that runoff estimated by the CN method could be a good predictor for gully erosion at the rainstorm event scale [57]. In this study, the annual average runoff estimated by the CN method (Q_a) was used to fit a nonlinear regression model for the long-term areal gully growth rate (R_A =0.301Q_a^0.562 S_d, R² = 0.530), suggesting that the long-term gully growth rate could be estimated with runoff and the slope of the drainage area as predictors. Soil and water conservation measures affect gully erosion by reducing runoff or slope gradients, which could be taken into account with the model presented in this study. However, it is difficult to accurately estimate runoff from the drainage area in the tableland of the Loess Plateau because soil and water conservation measures, including small reservoirs, could reduce runoff into the gullies, and there is sometimes piping erosion in the drainage areas. This can explain why the gully growth rate model built in this study with runoff as a predictor did not work as well as the models in previous studies [56,57]. This study mainly focused on the effects of topography, land uses and conservation practices with a reasonable assumption that soil properties varies slightly on the loess covered area [60]. The main soil type in the study area is the loessial soil that has a composition of more than 50% silt (0.002–0.05 mm) and less than 20% clay (<0.002 mm), and a porosity of approximately 50% [61], leading to very high infiltration capacity [61]. Nevertheless, further researches should be carried to investigate the variation of the soil properties and the infiltration rates caused by land use changes.

4.2. Topographic Thresholds of Gully Growth

The topographic threshold is the most common approach to understanding the critical condition for gully initiation and development [5,7,52]. Based on 45 growing gully heads and 25 stable gully heads, S-A relationships were fitted in this study, following the methods in previous research [7,52]. Parameters k and b showed very large variabilities in different environments [7], and variations in k seem mainly attributable to differences in land cover under the assumption that b is relatively constant [5,7]. The low k value indicated that the land cover condition in the study area was more prone to erosion [7]. For exponent b, the results of this study (b = 0.289) are comparable to those of several previous studies (

Table 7. Topographic threshold of gully erosion in published papers and this study.

Country	Study Area	k	b	Main Land Use Type	Reference
Belgium	Vlaams Brabant	0.050	0.400	Cropland	[62]
Spain	Cerro Tonosa	0.230	0.100	Cropland	[63]
USA	Standford Hills, California	0.180	0.500	Rangeland	[52]
China	Hilly gully region, Loess Plateau	0.184	0.239	Cropland	[29]
China	Hilly gully region, Loess Plateau	0.058	0.300	Cropland	[64]
China	Hilly gully region, Loess Plateau	0.053	0.379	Unpaved road 1	[57]
China	Tableland region, Loess Plateau	0.006	0.289	Apple orchard, cropland	This study 2

¹. Gully erosion on unpaved road with multiple land uses in the drainage area. ². These k and b values are for 70 gullies, including those that are stable and growing.

).

The S_g-Q_a relationship can express the threshold conditions better than the S_g-A relationship [57] because the drainage area is only a substitute for runoff [52]. However, runoff from the drainage area was not estimated accurately in the tableland of the Loess Plateau (Section 4.1) so that the S_g-Q_a relationship is not much better than the S_g-A relationship in this study.

4.3. Potentiality of Gully Growth

Gully erosion occurs when threshold conditions are exceeded and is controlled by the integrated effects of rainfall, flow hydraulics, topography, soil type, and land use [62,65,66,67]. In other words, a gully can be stable if the threshold is not exceeded. Topographic thresholds can partly explain the development of gullies. Figure 7a shows that growing gullies are far above the critical line, S_g = 0.006A^−0.289, indicating that, in terms of topographic conditions, these growing gullies have the potential to continue growing and gullies farther away from the threshold line have greater potential to grow. However, 25 gullies remained stable during 1969–2019, among which 15 gullies had terraces in their drainage area according to the images of 1969 and 2019, and 24 gullies had terraces in their drainage area according to the images of 2019. Terraces can change the effective drainage area by reducing runoff from the drainage area and then influencing gully erosion.

Since the GFGP and GSTP were put into practice in the tableland region of the Loess Plateau, soil and water conservation measures, including small reservoirs, terraces, shrub belts, and water barriers, have been widely adopted (Figure 8). Among 45 growing gullies from 1969 to 2010, only 17 continued to grow from 2010 to 2019, suggesting that the GFGP and GSTP reduced gully erosion to some extent. Gully erosion in the study area has been intervened with greatly by human activity. Some gullies were infilled and excavated by human activities directly, which are easily recognized. However, in most cases, gully development is influenced indirectly by soil and water conservation measures, land use changes, roads constructions, water conservancy facilities, etc. Quantifying of these effects need to be integrated with reliable runoff simulation model, which should be taken into consideration for future studies. On the other hand, studies have reported that several single rainfall events with high rainfall intensities promote the formation and development of gullies [56,65,68,69,70]. With the gully growth potential in terms of topographic conditions, whether soil and water conservation measures are effective for gully erosion under extremely high rainfall intensity needs further investigation. However, the results of this study are still helpful for preventing further gully erosion by dealing with gullies far above the threshold line.

5. Conclusions

In this study, high-resolution images were used to investigate gully growth rates from 1969 to 2019. Forty-five of 95 investigated gullies grew from 1969 to 2010 at rates ranging from 0.50 to 20.94 m²·yr⁻¹ (0.04 to 2.78 m·yr⁻¹), with an average of 5.66 m²·yr⁻¹ (0.30 m·yr⁻¹). Twenty-five gullies were stable, 21 gullies were infilled, and four were excavated by human intervention. The present drainage area, local slope, average drainage slope, annual runoff, and ratio of terraced area were all significantly different between the stable and growing gullies. For growing gullies, runoff is an important factor that influences the gully growth rates. The long-term areal gully growth rate (R_A) could be estimated using a nonlinear regression model with the annual average runoff (Q_a) and average slope of the drainage area (S_d) as predictors (R_A = 0.301Q_a^0.562 S_d, R² = 0.530). Based on 45 growing gullies and 25 stable gullies, the S_g-Q_a relationship was able to reveal the threshold conditions for gully growth. Based on the threshold conditions, all growing gullies still have the potential to keep growing, while soil and water conservation measures could change the threshold condition by reducing the effective drainage area. An increasing number of gullies would possibly remain stable in the future since GFGP and GSTP were launched. Many soil and water conservation measures (including terraces, small reservoirs, shrub belts, etc.) and change of cropland to apple orchards have strong effects on gully erosion mitigation. The results of this study could be helpful for preventing further gully erosion by dealing with gullies far above the threshold line.