Atmospheric Correction of Airborne Hyperspectral CASI Data Using Polymer, 6S and FLAASH

Abstract

Airborne hyperspectral data play an important role in remote sensing of coastal waters. However, before their application, atmospheric correction is required to remove or reduce the atmospheric effects caused by molecular and aerosol scattering and absorption. In this study, we first processed airborne hyperspectral CASI-1500 data acquired on 4 May 2019 over the Uljin coast of Korea with Polymer and then compared the performance with the other two widely used atmospheric correction approaches, i.e., 6S and FLAASH, to determine the most appropriate correction technique for CASI-1500 data in coastal waters. Our results show the superiority of Polymer over 6S and FLAASH in deriving the R_rs spectral shape and magnitude. The performance of Polymer was further evaluated by comparing CASI-1500 R_rs data with those obtained from the MODIS-Aqua sensor on 3 May 2019 and processed using Polymer. The spectral shapes of the derived R_rs from CASI-1500 and MODIS-Aqua matched well, but the magnitude of CASI-1500 R_rs was approximately 0.8 times lower than MODIS R_rs. The possible reasons for this difference were time difference (1 day) between CASI-1500 and MODIS data, higher land adjacency effect for MODIS-Aqua than for CASI-1500, and possible errors in MODIS R_rs from Polymer.

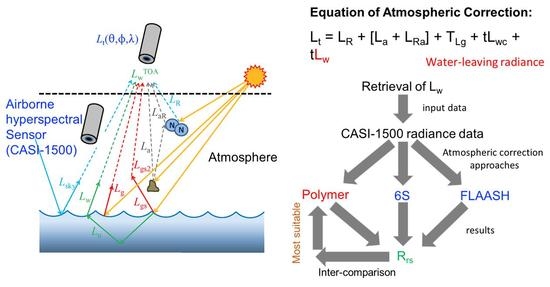
1. Introduction

Remote sensing is an effective tool for monitoring coastal waters, which are complex and highly variable ecosystems. Airborne hyperspectral sensors have several advantages over spaceborne sensors, and thus they play a vital role in remote sensing. First, imagery from airborne sensors are of a higher spatial resolution. For instance, the Compact Airborne Spectrographic Imager (CASI)-1500 has a spatial resolution that varies with flight altitude and can be 1 m × 1 m if the aircraft is at an altitude of approximately 2 km above the ground, whereas the spaceborne sensors such as SeaWiFS (Sea-viewing Wide Field-of-view Sensor) and MODIS (MODerate resolution Imaging Spectroradiometer) have a spatial resolution of 1 km × 1 km. This higher spatial resolution of airborne hyperspectral sensors makes them more desirable for coastal water applications [1,2].

The second advantage is that most airborne hyperspectral sensors are programmable in terms of the number and locations of spectral channels and their bandwidths. For example, 36 spectral bands may be acquired with 1 m × 1 m spatial resolution and a flight speed of 120 knots, whereas 48 spectral bands are possible at a flight speed of 90 knots. Therefore, for a given location, it is possible to adjust spectral channels and spectral resolutions as desired [3]. Another advantage is that the timing of airborne data acquisition can be controlled, so adverse weather conditions such as cloud cover, rain, and haze can be avoided, whereas data collected from spaceborne sensors under these conditions are often invalid. Disadvantages of airborne remote sensing compared to satellite and in situ sampling include high cost and lengthy data processing time due to large data volume. Additionally, airborne remote sensing has smaller spatial coverage than satellite sampling. Despite this, airborne remote sensing is particularly useful for mapping coastal waters, as spatial and spectra resolutions are demanding in these areas.

However, atmospheric correction is critical before the quantitative application of airborne hyperspectral data. Atmospheric correction removes or reduces the effects caused by molecular and particular scattering and absorption, thus converting the radiances measured by the sensors to remote sensing reflectances (R_rs) of the target surfaces [4,5]. In the past three decades, atmospheric correction algorithms have been developed that range from empirical models to rigorous physically based radiative transfer models [6,7,8,9,10,11,12,13]. Some of the most popular atmospheric correction approaches include Polymer (POLYnomial based algorithm applied to MERIS), 6S (Second Simulation of a Satellite Signal in the Solar Spectrum), FLAASH (Fast Line-of-sight Atmospheric Analysis of Spectral Hypercubes), and ATCOR (ATmospheric CORrection) [14,15,16,17]. A few studies were carried that compare several radiative transfer models using medium and high-resolution data. For instance, Eugenio et al. [18] implemented 6S, FLAASH, and ATCOR; and Marcello et al. [19] implemented DOS (Dark Object Subtraction), QUAC (Quick Atmospheric Correction), 6S, FLAASH, and ATCOR for high-resolution WordView-2, a satellite-based imaging system with a spatial resolution of 0.46 m in the panchromatic (PAN) band and 1.84 m in eight multispectral (MS) channels. Nguyen et al. [20] evaluated 6S, FLAASH, and DOS using Landsat ETM+, which has a spatial resolution of 30 m for band 1 to 7 and a resolution of 15 m for the panchromatic band 8. In general, radiative transfer models outperform empirical methods, but no single algorithm performs best in all scenarios [18].

In this study, the performance of three atmospheric correction algorithms, i.e., Polymer, 6S, and FLAASH, were evaluated using a CASI-1500 imagery acquired on 4 May 2019 over the Uljin coast, the southeastern coast of Korea (Figure 1). Polymer was purposed to recovering ocean colour from the top-of-atmosphere signal measured by satellite sensors in the visible spectrum. One of the strengths of this algorithm is the possibility to recover ocean colour in the presence of sun glint. It has been applied to multiple sensors from ESA (MERIS/ENVISAT, MSI/Sentinel-2, and OLCI/Sentinel-3), NASA (SeaWiFS, MODIS/Aqua, VIIRS), and the Korean Geostationary Ocean Colour Imager (GOCI) [14,21,22,23]. However, to our knowledge, Polymer has not yet been applied to airborne hyperspectral sensors. It is to be expected that the atmospheric correction procedures useful for satellites can be valid for airborne sensors, although satellites and airborne sensors are at different altitudes. The 6S algorithm is one of the most widely used, rigorously validated, and heavily documented radiative transfer codes [24], although it is mainly applied to satellite sensors as well [18,25,26,27]. FLAASH has been applied to airborne hyperspectral data [28]. However, it does not separate the surface Fresnel reflectance from the target reflectance, which is acceptable for land areas but invalid for water areas [29]. In addition, FLAASH uses homogeneous aerosol properties derived from a dark target for the entire scene [30].

The waters along the Uljin coast are shallow with water depths < 20 m (Figure 1b). Seaweed is the dominant primary producer in this ecosystem, but whitening of coralline algae has adversely affected this region. Therefore, whitening detection is necessary to better understand the degradation of the ecosystem and help the local government to develop mitigation measures. In a recent study, Kim et al. [31] investigated the whitening of the Uljin coast via benthic mapping using CASI-1500 data, atmospherically corrected using FLAASH. However, the resulting CASI-1500 R_rs data were not validated as no field measurements of R_rs were available.

The objective of this study was to find the most suitable atmospheric correction algorithm to apply to CASI-1500 data for future studies in shallow coastal ecosystems. Additionally, for the first time, we applied Polymer to airborne hyperspectral data.

2. Materials and Methods

2.1. Airborne Hyperspectral Data

CASI-1500 hyperspectral data were acquired at 14:17:47 (+9 h GMT) on 4 May 2019, for an area ranging from 36.84°N to 37.05°N latitude and 129.41°E to 129.46°E longitude (Figure 1). The data were collected at an altitude of 2 km with a spatial resolution of 1 m across 48 spectral bands with a full width at half maximum of 7.2 nm (

Table 1. Spectral bands and width of the CASI-1500 sensor for data acquired on 4 May 2019.

Band Number	Center Wavelength (nm)	Band Number	Center Wavelength (nm)	Band Number	Center Wavelength (nm)	Band Number	Center Wavelength (nm)	Full Width at Half Maximum (nm)
1	370.2	13	542.8	25	715.1	37	887.1	7.2
2	384.6	14	557.2	26	729.4	38	901.5
3	399	15	571.5	27	743.7	39	915.8
4	413.4	16	585.9	28	758.1	40	930.2
5	427.8	17	600.3	29	772.4	41	944.5
6	442.2	18	614.6	30	786.8	42	958.8
7	456.6	19	629.0	31	801.1	43	973.2
8	471	20	643.3	32	815.4	44	987.5
9	485.3	21	657.7	33	829.8	45	1001.9
10	499.7	22	672.0	34	844.1	46	1016.2
11	514.1	23	686.4	35	858.5	47	1030.6
12	528.5	24	700.7	36	872.8	48	1044.9

).

Pre-processing of the CASI-1500 data included radiometric calibration, which converted digital number (DN) into spectral radiance unit (SRU, μw cm⁻² sr⁻¹ nm⁻¹) with a scale factor of 1000, and geometric calibration using the GEOCORR program, which geo-referenced the data to UTM WGS84 [31]. Use of CASI-1500 also required use of inputs from MODIS-Aqua described in Section 2.2.

2.2. Satellite and Reanalysis Data

MODIS (Moderate Resolution Imaging Spectroradiometer), a key instrument aboard the Aqua (EOS PM) satellite (MODIS/Aqua), has a spatial and temporal resolution of 1 km and 1 day, respectively. The Level-1A data at 5:00 (GMT) on 3 May 2019 were obtained from the NASA Goddard Space Flight Center. They were converted into Level-1B data using the OCSSW tools in the SeaDAS 7.5.3 software, and finally into Level-1C data that included all the necessary radiometric corrections using the l2gen command in the Polymer codes [14,21]. The Level-1C data were further processed to Level-2 data using the Polymer approach. These Level-2 R_rs data had a spatial resolution of 1 km at bands 412, 443, 488, 531, 547, 667, 678, 748, 859, and 869 nm, 500 m at bands 469 and 555 nm, and 250 m at band 645 nm. MODIS R_rs data at all bands except for band 678 were compared with the CASI R_rs data obtained after applying the Polymer atmospheric correction to radiance data. The R_rs at band 678 was not compared because Polymer failed to retrieve CASI R_rs at this band.

It should be noted that the MODIS and CASI data were acquired on different dates (1 day difference) because no valid MODIS data were available for the 4 May 2019 when the CASI data were collected. Therefore, when comparing the MODIS and CASI R_rs data, we were mindful that this time difference needed to be considered in our analysis. In addition, the spatial resolutions of CASI and MODIS sensors are much different (1 m vs. 1 km). To compare CASI and MODIS R_rs, we averaged CASI values within the MODIS 1 km pixel.

Next, the 6S atmospheric correction approach was applied to MODIS atmosphere and chlorophyll-a (Chl-a) products as well as reanalysis Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-2) products provided by the National Aeronautics and Space Administration Goddard Space Flight Center. Specifically, we used two MODIS atmosphere products, including MYD05 (water vapour) and MYD07 (total ozone) at 4:05 (GMT) on 4 May 2019, approximately 1 h before the acquisition of CASI-1500 data. The spatial resolution of MYD05 and MYD07 was 0.05°. As the MODIS aerosol product from MYD04 (aerosol optical thickness at 550 nm, aot_550) was not available for the same day, we used the hourly MERRA-2 aerosol product (Total Aerosol Extinction AOT [550 nm]) with a much coarser spatial resolution of 0.5° × 0.625°. Additionally, we also used MODIS Level-2 Chl-a product on 3 May 2019 (5:00 GMT) and hourly MERRA-2 wind speed product (U2M and V2M) on 4 May 2019. The spatial resolution of these products was 1 km × 1 km and 0.5° × 0.625°, respectively.

2.3. Polymer Atmospheric Correction Approach

Polymer proved advantageous in recovering pixels under sun glint compared to traditional atmospheric correction algorithms. In addition, it uses a polynomial function of wavelength (λ) and an ocean reflectance model to calculate water surface reflectance based on a spectral matching technique. A brief summary of the Polymer procedure is as follows:

First, an initial atmospheric correction is carried out for the top-of-atmosphere reflectance (${\rho }_{TOA}\left(\lambda \right)$) which is decomposed according to the following equation:

$${\rho }_{TOA}\left(\lambda \right)=t_{oz}\left(\lambda \right)\left[{\rho }_{mol}\left(\lambda \right)+T\left(\lambda \right){\rho }_{gli}+{\rho }_{aer}\left(\lambda \right)+{\rho }_{coupl}\left(\lambda \right)+t\left(\lambda \right){\rho }_w{}^{+}\left(\lambda \right)\right]$$

(1)

where $t_{oz}\left(\lambda \right)$ is the transmittance of ozone; ${\rho }_{mol}\left(\lambda \right)$, ${\rho }_{gli}$, ${\rho }_{aer}\left(\lambda \right)$, ${\rho }_{coupl}\left(\lambda \right)$, and ${\rho }_w{}^{+}\left(\lambda \right)$ are the reflectance of Rayleigh scattering, sun glint, non-absorbing aerosols, and the various couplings between sun glint, molecules, and aerosols, as well as of the water above the water-air interface, respectively; $T\left(\lambda \right)$ and $t\left(\lambda \right)$ are the direct transmission factors and the total (direct and diffuse) transmission for atmospheric scattering, respectively. The $t_{oz}\left(\lambda \right), {\rho }_{mol}\left(\lambda \right)$, and ${\rho }_{gli}$ were obtained using the Successive Order of Scattering (SOS) radiative transfer model in [14].

After the initial atmospheric correction, the remaining term (${\rho }^{\prime }\left(\lambda \right)$) is expressed by the following equation:

$${\rho }^{\prime }\left(\lambda \right)=△{\rho }_{gli}\left(\lambda \right)+{\rho }_{aer}\left(\lambda \right)+{\rho }_{coupl}\left(\lambda \right)+t\left(\lambda \right){\rho }_w{}^{+}\left(\lambda \right)$$

(2)

Furthermore, the first three terms and the last term are modelled by $T_0\left(\lambda \right)c_0+c_1{\lambda }^{-1}+c_2{\lambda }^{-4}$ and ${\rho }_{wmod}{}^{+}\left(\left[chl\right],b_{bNC},\lambda \right),$ respectively. The $T_0\left(\lambda \right)$ is a transmission factor that can be calculated using the formula in [14]. The variables Chl and b_bNC represent the chlorophyll-a concentration and the backscattering coefficient of non-covarying particles, respectively. Therefore, ${\rho }^{\prime }\left(\lambda \right)$ is also expressed by the following equation:

$${\rho }^{\prime }\left(\lambda \right)=T_0\left(\lambda \right)c_0+c_1{\lambda }^{-1}+c_2{\lambda }^{-4}+t\left(\lambda \right){\rho }_{wmod}{}^{+}\left(\left[chl\right],b_{bNC},\lambda \right)$$

(3)

The spectral matching technique retrieves c₀, c₁, c₂, chl, and b_bNC, and finally ${\rho }_w{}^{+}\left(\lambda \right)$ is obtained based on these parameters.

To quality control the MODIS-Aqua R_rs after application of the Polymer atmospheric algorithm, several criteria were established to exclude the R_rs data that did not meet our strict requirements: (1) High sun glint (L_gn > 0.005 sr⁻¹), where L_gn is a sun glint coefficient calculated with the model by Cox and Munk [32] and wind [33]; (2) Thick clouds (ρ_TOA(869) − t_oz(869)ρ_mol(869) > 0.027); (3) high air mass (1/cos(θ_s) + 1/cos(θ_v) > 5), where θ_s and θ_v are solar zenith angle and sensor zenith angle, respectively; and (4) θ_s > 88°. The criteria for quality control of CASI R_rs after application of the Polymer atmospheric algorithm were the same as for MODIS-Aqua R_rs but the band used for (2) was 873 nm, which is the closest band to the MODIS-Aqua 869 nm band.

The main modification that we undertook when using Polymer for processing CASI data is that we used the 6S output parameters, including $t_{oz}\left(\lambda \right)$, ${\rho }_{mol}\left(\lambda \right)$, ${\rho }_{gli}$, transmission of Rayleigh scattering ($T_{mol}\left(\lambda \right)$), and Rayleigh optical thickness from the top-of-atmosphere to sensor (τ_{m_sensor}(λ)), and total Rayleigh optical thickness (τ_{m_total}(λ)) from the top-of-atmosphere to sea surface, for the initial atmospheric correction and Polymer atmospheric correction model. The difference between τ_{m_total}(λ) and τ_{m_sensor}(λ) (τ_{m_total}(λ) − τ_{m_sensor}(λ)) is the Rayleigh optical thickness from sensor to sea surface.

The CASI radiance data were converted into apparent reflectance using the following equation:

$${\rho }^{*}\left(\lambda \right)=L/E_{s\_sensor}$$

(4)

where L and E_{s_sensor} represent the CASI radiance and the simulated solar downwelling irradiance at the sensor altitude, respectively.

We calculated E_{s_sensor} using the following equations [14,34]:

$$E_{s\_sensor}\left(\lambda \right)=E_{sol}{}^{dir}\left(\lambda \right)+E_{sol}{}^{diff}\left(\lambda \right)$$

(5)

$$E_{sol}{}^{dir}\left(\lambda \right)={\mu }_s{E}_{s\_TOA}{T}_0{}^{dir}\left(\lambda \right)$$

(6)

$$E_{sol}{}^{diff}\left(\lambda \right)={\mu }_s{E}_{s\_TOA}{T}_0{}^{diff}\left(\lambda \right)$$

(7)

$$E_{s\_TOA}=\frac{{{\displaystyle \int }}_{{\mathsf{\lambda }}_1}^{{\mathsf{\lambda }}_2}E\left(\lambda \right)S\left(\lambda \right)d\lambda }{{{\displaystyle \int }}_{{\mathsf{\lambda }}_1}^{{\mathsf{\lambda }}_2}S\left(\lambda \right)d\lambda }$$

(8)

$$T_0{}^{dir}\left(\lambda \right)=exp\left[-\left({\tau }_{m\_total}\left(\lambda \right)\right)-{\tau }_{m\_sensor}\left(\lambda \right)\right)\times \left(\frac{1}{{\mu }_s}+\frac{1}{{\mu }_v}\right)]$$

(9)

$$T_0{}^{diff}\left(\lambda \right)=exp[-0.5\times \left({\tau }_{m\_total}\left(\lambda \right)-{\tau }_{m\_sensor}\left(\lambda \right)\right)\times \left(\frac{1}{{\mu }_s}+\frac{1}{{\mu }_v}\right)]$$

(10)

where $E_{sol}{}^{dir}\left(\lambda \right)$ and $E_{sol}{}^{diff}\left(\lambda \right)$ are the direct and diffuse solar downwelling irradiance at the sensor altitude, respectively; E_{s_TOA} is the solar downwelling irradiance at the top-of-atmosphere; $T_0{}^{dir}\left(\lambda \right)$ and $T_0{}^{diff}\left(\lambda \right)$ are the direct and diffuse transmittance factors, respectively; E(λ) and S(λ) are the 1985 Wehrli Standard Extraterrestrial Solar Irradiance Spectrum and spectral response function of CASI, respectively; λ₁ and λ₂ are the start and end wavelength of each CASI band, respectively; and μ_s and μ_v are the cosine of solar zenith angle and sensor zenith angle, respectively.

2.4. 6S Atmospheric Correction Approach

The 6S algorithm is one of the most widely used, rigorously validated, and elaborately documented radiative transfer codes [24]. The vector version of 6S was used in this study and it accounts for radiation polarization, in contrast to the scalar version of 6S. Accuracy of the atmospheric correction results by 6S is affected by the input atmospheric parameters, including the aerosol optical thickness and total amount of water vapour and ozone. However, field measurements of these parameters are often unavailable. Therefore, we used satellite and reanalysis atmospheric products (as described in Section 2.2) in this study. Furthermore, 6S simulated the atmospheric parameters at the airborne sensor altitude that were used as the final 6S input.

The parameter settings of 6S for the CASI-1500 imagery are described as below (

Table 2. Description of the 6S input parameters for CASI-1500 data collected on 4 May 2019.

Parameters	Data Source	Spatial Resolution	Temporal Resolution	Value
Solar zenith angle	–	–	–	33.663°
Solar azimuth angle	–	–	–	239.218°
Sensor zenith angle	–	–	–	By pixel
Sensor azimuth angle	–	–	–	270°
Total water vapour	MYD05	1 km × 1 km	Daily	1.77 cm
Total ozone	MYD07	1 km × 1 km	Daily	0.34 cm-atm
Aerosol model	–	–	–	Maritime
aot_550	MERRA-2	0.5° × 0.625°	Hourly	0.32
Wind speed	MERRA-2	0.5° × 0.625°	Hourly	1.91 m s−1
Wind azimuth angle	–	–	–	313.004°
Chl-a concentration	MODIS-Aqua Level-2	1 km × 1 km	Daily	3.76 mg m−3
Sea water salinity	–			34.3 ppt

).

The solar zenith angle and solar azimuth angle were calculated from one-pixel location in the CASI-1500 imagery using Pysolar codes. Sensor zenith angle and sensor azimuth angle were calculated for each pixel. The former was obtained by dividing the DN values of the CASI-1500 NAD (NADIR Channel) imagery by 1000, whereas the latter using the formula acquired from https://www.omnicalculator.com/other/azimuth#what-is-the-azimuth, accessed on 25 August 2021. In general, the sensor azimuth angles were 0° for the nadir view pixels, 90° for the pixels on the left side of the nadir view pixels, and 270° for the pixels on the right side of the nadir view pixels. As the location points for validation (red symbols in Figure 1) were generally on the right side of the nadir view pixels, the sensor azimuth angle was set to be 270°. For total water vapour, total ozone, and Chl-a concentration, averaged values from the pixels covering the CASI-1500 imagery were used. For aot_550 and wind speed, a single value from the pixel covering the whole CASI-1500 imagery was used. In addition, the aerosol model was chosen to be Maritime based on the location and climate of the study area. Finally, sea water salinity was set to be 34.3 ppt for each pixel.

The 6S model is expressed by the following equation [18,35]. Reference to wavelength (λ) is omitted for clarity of the equation:

$${\rho }_{TOA}\left({\theta }_s,{\theta }_v,\mathsf{\Delta }\varphi \right)=t_g\left({\theta }_s,{\theta }_v\right)\left\{{\rho }_a\left({\theta }_s,{\theta }_v,\Delta \varphi \right)+\left[e^{\frac{-\tau }{{\mu }_s}}+td\left({\theta }_s\right)\right]\frac{{\rho }_{su}{e}^{\frac{-\tau }{{\mu }_v}}+{\rho }_{e}td\left({\theta }_v\right)}{1-{\rho }_{e}S}\right\}$$

(11)

where ${\rho }_{TOA}$, ${\rho }_a,{\rho }_{su}, and {\rho }_e \mathrm{represent}$ the top-of-atmosphere reflectance, atmospheric reflectance, surface reflectance, and a homogenous environment of reflectance, respectively; $\mathsf{\Delta }\varphi$ represents the difference between solar and sensor azimuth; $t_g \mathrm{represents} \mathrm{the} \mathrm{total}$ transmissivity of the gases, considering the absorption of different gases; $\tau \mathrm{represents}$ the atmospheric thickness; $td\left({\theta }_s\right) \mathrm{and} td\left({\theta }_v\right)$ represent the diffuse transmittance of the atmosphere; S represents the spherical albedo of the atmosphere; and the $1-{\rho }_{e}S$ term considers the multiple scatterings between the surface and the atmosphere.

2.5. FLAASH Atmospheric Correction Approach

FLAASH is available in ENVI and it incorporates MODTRAN4 radiative transfer code [34]. The FLAASH model is expressed by the following equation. Again, reference wavelength (λ) is also omitted for simplicity:

$$L=(\frac{A\rho }{1-{\rho }_{e}S})+(\frac{B{\rho }_e}{1-{\rho }_{e}S})+L_a$$

(12)

where L represents the radiance at the sensor pixel; $\rho$ represents the pixel surface reflectance; ${\rho }_e$ represents an average surface reflectance for the pixel and the surrounding region; S represents the spherical albedo of the atmosphere; $L_a$ represents the radiance backscattered by the atmosphere; and A and B are coefficients that depend on atmospheric and geometric conditions.

For the FLAASH parameter setting, any of the standard MODTRAN model atmosphere and aerosol types can be chosen to represent a scene and a unique MODTRAN solution is computed for each image. In this study, mid-latitude summer and maritime were selected for the atmospheric and aerosol models, respectively. The initial visibility value was obtained from the 6S simulation, which used the reanalysis aot_550 as the input data. Water vapour was retrieved using the water absorption feature at 940 nm.

The parameter settings of FLAASH applied to CASI-1500 imagery are described in

Table 3. Description of the FLAASH input parameters applied to CASI-1500 data collected on 4 May 2019.

Parameter	Value
Image center location	37.05057344°N, 129.41963701°E.
Sensor altitude	2 km
Ground elevation	0.01 km
Pixel size	1 m
Flight date	4-May-19
Flight time GMT	5:17:47
Atmospheric model	Mid-Latitude Summer
Aerosol model	Maritime
Aerosol retrieval	None
Initial visibility	14.85 km
Water retrieval	Yes
Water absorption feature	940 nm
Modtran resolution	5 cm−1
Modtran multiscatter model	Scaled DISORT
DISCORT streams number	8

.

2.6. Statistical Analysis

To quantitatively measure the spectral similarity between the CASI-1500 and MODIS R_rs spectra obtained by Polymer, we calculated the cosine distance using the following equation [23,36]:

$$\cos (\alpha )=\frac{{\displaystyle \sum _i^N(Rr{s}_{CASI,i}Rr{s}_{MODIS,i})}}{\sqrt{{\displaystyle \sum _i^N{(Rr{s}_{CASI,i})}^2}}\sqrt{{\displaystyle \sum _i^N{(Rr{s}_{MODIS,i})}^2}}}$$

(13)

where α represents the angle between the CASI R_rs spectrum (R_rsCASI,i ) and MODIS R_rs spectrum (R_rsMODIS,i). A closer match of the two spectra is indicated by a smaller α and a bigger cos(α).

3. Results

The results from applying the atmospheric correction approaches—Polymer, 6S, and FLAASH—to CASI-1500 data were compared. MODIS data were processed with Polymer as the atmospheric algorithm was used to evaluate the performance of Polymer for CASI-1500 data.

3.1. CASI-1500 Radiance and Apparent Reflectance

CASI-1500 radiance data (Figure 1a) were first converted into apparent reflectance data and then processed using Polymer to obtain the CASI-1500 R_rs data.

Radiance data were collected from eight locations, i.e., No. 1, No. 9, No. 17, No. 25, No. 33, No. 41, No. 49, and No. 57 shown as evenly distributed (from top to bottom) red symbols on the CASI radiance image in Figure 1. The radiance spectra (Figure 2a), had similar spectral shapes but different magnitudes. Specifically, the spectra peaked at the green band near 500 nm, which is typical for coastal waters. Several spectral valleys seen near 720 nm, 760 nm, 820 nm, and 940 nm are due to absorption by water vapour and oxygen. The apparent radiance data had similar spectral shapes as the radiance data.

3.2. Polymer, 6S, and FLAASH Results for CASI-1500

To compare the atmospheric correction approaches, the entire CASI-1500 radiance imagery (Figure 1a) was corrected using Polymer, 6S, and FLAASH, after which R_rs data were extracted from 57 pixels, i.e., the red symbols in Figure 1a. All R_rs spectra from the 57 pixels were averaged and plotted with error bars of one standard deviation (Figure 3). The R_rs spectra from wavelengths above 900 nm are not shown because the CASI-1500 data were usually unstable and not informative in that wavelength range.

The spectral shape of R_rs after applying the Polymer algorithm (Figure 3a) was generally consistent with that of CASI-1500 radiance and apparent reflectance (Figure 2), but the magnitude of R_rs was smaller at all spectral bands. In contrast, although R_rs from both 6S and FLAASH (Figure 3b,c) had similar spectral shape and magnitude, they differed greatly from R_rs obtained using Polymer both in spectral shape and magnitude. In addition, R_rs using 6S and FLAASH were negative in the blue bands (400–500 nm) and higher than apparent reflectance values in other bands.

CASI R_rs values using 6S and FLAASH were overcorrected in the blue bands. This was probably caused by inaccurate input parameters, particularly the atmospheric parameters. Therefore, we examined a variation of CASI R_rs with aot_550 and water vapour for 6S (Figure 4a,b) and visibility for FLAASH (Figure 4c) at a test point (129.435°E, 36.985°N). For 6S atmospheric correction, the referenced aot_550 and water vapour values were 0.316 and 1.64 cm, respectively; for FLAASH atmospheric correction, the referenced visibility value was 14.85 km. The other two atmospheric values in each plot were 0.5 times and 1.5 times of the referenced value, respectively.

For 6S atmospheric correction, the magnitude of the entire R_rs spectrum increased and decreased significantly with the decrease and increase in aot_550 (Figure 4a), respectively, whereas the magnitude of R_rs changed little with variation of water vapour. Similarly, for FLAASH atmospheric correction, the magnitude of the entire R_rs spectrum increased significantly with the increase in visibility.

3.3. Comparison of the Polymer Results for CASI-1500 and MODIS

Previously, Zhang et al. [22] applied Polymer to MODIS data and compared its performance with in situ R_rs to conclude that it did not perform better than the standard NASA atmospheric correction algorithm (traditional near-infrared (NIR) approach [37]), at blue bands but was comparable at green and red bands. Therefore, they proposed using Polymer as a surrogate for the NASA NIR approach when MODIS R_rs data were limited.

In this study, due to lack of in situ R_rs data, we evaluated the performance of Polymer by comparing the R_rs results from CASI-1500 and MODIS. MODIS bands selected were 412, 443, 488, 531, 547, 667, 748, and 869 nm, and the corresponding CASI-1500 bands were 413, 442, 485, 529, 543, 672, 744, and 873 nm. Regarding the different pixel resolution of the two sensors, spatial distribution of CASI R_w (water-leaving reflectance) using Polymer was examined. As the data volume of whole CASI radiance image (Figure 1) was too big to process at one time, the image was divided into eight parts. Images of CASI R_w at 413, 442, 485, 529, 543, and 672 nm were made for one part of the whole area (129.428°–129.438°E, 37.002°–37.027°N) (Figure 5).

Spatial variability of R_w at each band was observed. To quantify the variability, pixel and averaged R_rs were compared for eight points (No. 4, No. 5, No. 6, No. 7, No. 8, No. 9, No. 10, and No. 11) in each R_w image (Figure 6). In general, the pixel and averaged CASI R_rs showed similar spectral shape and magnitude for each point. Therefore, pixel CASI R_rs was compared with pixel MODIS R_rs for simplifying data processing (Figure 7).

Despite being measured on different days, R_rs spectra from CASI-1500 and MODIS generally matched except for inconsistencies at 485 and 744 nm. In addition, across the entire spectrum, MODIS R_rs values were much higher than CASI-1500 R_rs values. At 488 nm for instance, MODIS R_rs was approximately 0.007 sr⁻¹, whereas the CASI-1500 R_rs at 485 nm was 0.002 sr⁻¹.

The correlation between the CASI-1500 and MODIS R_rs spectra (Figure 8) was statistically significant (R² = 0.98), but the slope (0.21) was low, suggesting that the CASI-1500 R_rs were generally 0.8 times lower than MODIS R_rs. We further calculated the cosine distance between the two spectra and the cos(α) was approximately 0.99, which suggested that the two spectra were closely matched.

3.4. Variation of Polymer Results with Aerosol and Water Vapor for CASI-1500

For understanding the discrepancy between CASI-1500 and MODIS R_rs at each band, the variation in CASI-1500 R_rs with aot_550 and water vapour was investigated (Figure 9). The processing of CASI-1500 radiance data (as described in Section 2.3) was undertaken again with various aot_550 values, including 0, 0.01, 0.05, 0.1, 0.2, 0.3, and 0.4, and various water vapour values, including 0, 1, 1.5, 2, 3, and 4 cm, for the 6S input. The R_rs spectra obtained by applying Polymer to CASI-1500 R_rs for test locations showed that variation in CASI-1500 derived R_rs spectra due to aerosols and water vapour was small.

4. Discussion

4.1. Comparison among Polymer, 6S, and FLAASH

In this study, we applied Polymer to airborne hyperspectral CASI-1500 data and compared the resulting R_rs to two other widely used atmospheric correction approaches, i.e., 6S and FLAASH. The spectral shape of CASI-1500 R_rs using Polymer (Figure 3a) was similar to that of CASI-1500 apparent reflectance (Figure 2b), suggesting that the atmospheric effects influencing CASI-1500 radiance data on the acquisition day might be small. Moreover, the spectral shapes of CASI-1500 R_rs and MODIS R_rs using Polymer were highly correlated statistically, suggesting that the R_rs derived using Polymer were accurate.

In contrast, both 6S and FLAASH underestimated CASI-1500 R_rs, with negative values in the blue bands (400–500 nm). The R_rs values at other wavelengths were even larger than the CASI-1500 apparent reflectances, a clear indication that these two atmospheric correction approaches were estimating R_rs erroneously. Therefore, we conclude that the performance of Polymer is better than the performance of 6S and FLAASH. Despite the superior performance of Polymer, rigorous validation with in situ R_rs is necessary, which we plan to carry out when in situ R_rs data become available.

Polymer was originally designed to retrieve ocean colour in the presence of sun glint using MERIS data. The author concluded that Polymer greatly increased the spatial coverage of MERIS measurements for ocean colour and that the accuracy of retrieved data was not significantly reduced in high glint areas and remained the same as the standard algorithm outside sun glint areas [14]. The performance of Polymer was further evaluated by applying it to other satellite sensors. A recent study [22] compared Polymer with the traditional near-infrared (NIR) approach for MODIS-Aqua data and reported that Polymer did not perform better at blue bands but was comparable at green and red bands. Therefore, MODIS R_rs from Polymer was considered as reliable, at least not worse. The performance of Polymer to CASI data was then evaluated by comparing CASI R_rs with MODIS R_rs. However, CASI and MODIS R_rs showed big difference in their magnitude though their spectral shapes were similar. One possible cause for this difference may be errors in the MODIS R_rs.

Several studies [19,20] have compared R_rs after application of 6S and FLAASH to medium and high-resolution data. Recently, Eugenio et al. [18] applied 6S and FLAASH to WorldView-2 high-resolution satellite data and validated the atmospheric correction results with fields above water R_rs. They reported that both approaches achieved excellent results, although 6S produced slightly superior results. Our sub-optimal results using 6S and FLAASH for CASI-1500 hyperspectral imagery could be because the atmospheric products used were not accurate and the algorithms did not apply to these waters. In the future, to obtain more realistic atmospheric products, we need to consider two approaches. One is to make field measurements during CASI-1500 overflights, and the other is to develop algorithms to retrieve atmospheric products from CASI-1500 data.

4.2. Discrepancy of the CASI-1500 and MODIS R_rs with Polymer

The magnitude of CASI-1500 R_rs was approximately 0.8 times lower than that of MODIS R_rs (Figure 8). The possible reasons include: (1) dfference in the acquisition time of CASI-1500 versus MODIS data, the CASI-1500 data used was one day later than the MODIS data; (2) MODIS pixel size (1 km × 1 km) is much coarser than that of CASI-1500 (1 m × 1 m); (3) atmospheric products, such as MODIS water vapour and reanalysis aot_550, were also of much coarser spatial resolution than CASI-1500 data, which might affect the 6S output parameters and thus the atmospheric correction of CASI-1500 data with Polymer; (4) satellite measurements of coastal waters near land/water surfaces suffer from land adjacency effects [38], thus the MODIS 1 km pixels will most likely be affected by the adjacency and contamination of land signals much more than the low altitude and high resolution CASI data; and (5) errors in MODIS R_rs from Polymer. However, as we investigated the pixel CASI R_rs and averaged CASI R_rs within MODIS 1 km pixel were similar in spectral shape and magnitude, and the variation in R_rs using Polymer and CASI-1500 data with various values of aot_550 and water vapour and found them to be very small (Figure 6), we conclude that the discrepancies in R_rs between CASI-1500 and MODIS R_rs may be due to (1), (4), and (5).

5. Conclusions

Atmospheric correction may be required before application of airborne hyperspectral data analysis. The traditional atmospheric correction approach for CASI data has been FLAASH. However, the performance of FLAASH depends on the accuracy of input atmospheric parameters, including aerosol, water vapour, and ozone, which are often unavailable during the acquisition of airborne data.

Therefore, in this study, we evaluated three of the most widely used atmospheric correction approaches, i.e., Polymer, 6S, and FLAASH, and take the position that Polymer was the most suitable for application to CASI-1500 data. We further evaluated Polymer by comparing the R_rs derived from CASI-1500 and MODIS after using this atmospheric correction. Spectral shapes of R_rs from both sensors correlated significantly, although the magnitude of CASI-1500 R_rs was much lower than that of MODIS R_rs. We ascribe this difference to the one day difference in data acquisition between the two sensors, higher land adjacency effect for MODIS than for CASI-1500, and possible errors in MODIS R_rs from Polymer.

Our future plans include collecting in situ R_rs data to validate R_rs from CASI-1500 after application of the Polymer atmospheric correction, after which we will continue to modify the Polymer algorithm to improve its atmospheric correction and ocean reflectance models. In case of the atmospheric correction model, we plan to remove or reduce the effect of sky radiance, whereas for the ocean reflectance model, we plan to address the bottom reflectance effect in shallow waters.