Quiet Ionospheric D-Region (QIonDR) Model Based on VLF/LF Observations

Abstract

The ionospheric D-region affects propagation of electromagnetic waves including ground-based signals and satellite signals during its intensive disturbances. Consequently, the modeling of electromagnetic propagation in the D-region is important in many technological domains. One of sources of uncertainty in the modeling of the disturbed D-region is the poor knowledge of its parameters in the quiet state at the considered location and time period. We present the Quiet Ionospheric D-Region (QIonDR) model based on data collected in the ionospheric D-region remote sensing by very low/low frequency (VLF/LF) signals and the Long-Wave Propagation Capability (LWPC) numerical model. The QIonDR model provides both Wait’s parameters and the electron density in the D-region area of interest at a given daytime interval. The proposed model consists of two steps. In the first step, Wait’s parameters are modeled during the quiet midday periods as a function of the daily sunspot number, related to the long-term variations during solar cycle, and the seasonal parameter, providing the seasonal variations. In the second step, the output of the first step is used to model Wait’s parameters during the whole daytime. The proposed model is applied to VLF data acquired in Serbia and related to the DHO and ICV signals emitted in Germany and Italy, respectively. As a result, the proposed methodology provides a numerical tool to model the daytime Wait’s parameters over the middle and low latitudes and an analytical expression valid over a part of Europe for midday parameters.

1. Introduction

The ionosphere is the upper atmospheric layer that, due to its electrical properties, affects the propagation of electromagnetic waves [1,2]. This property is of high significance in many fields that include application of data obtained by different kinds of microwave signals (like the Global Navigation Satellite System (GNSS) [3,4,5,6,7,8] and Synthetic aperture radar (SAR) interferometry meteorology [9]), and both signal and ionospheric characteristics have influence on changes in signal propagation within this medium. For example, telecommunication signals emitted from the ground are affected by the ionosphere below the signal reflection height, while satellite signals are primarily affected by the F-region due to the largest values of electron density in the altitude domain located in this region.

Research of ionospheric properties is a very complex task because of permanent influences coming from outer space and different terrestrial layers. For this reason, it is of crucial importance to include as many observational data as possible in their modeling. For example, although the unperturbed D-region has not visible influences on satellite signal propagation, the recent results presented in Reference [10] show the importance of inclusion of its effects during intensive disturbances that are not considered in existing models (see, for example, References [11,12,13]).

Application of the specific technique for remote sensing of the ionosphere depends on the altitude domain. In addition, the choice of a particular analysis methodology depends on temporal and spatial characteristics of the collected data. The remote sensing of the lower ionosphere based on the propagation of very low/low frequency (VLF/LF) radio signals is an effective means to collect continuous observations the covering areas. These signals can propagate several thousand kilometres within the Earth-ionosphere waveguide, and the global observational setup is based on numerous worldwide located transmitters, and receivers. The VLF/LF receivers have the possibility of simultaneous monitoring of several signals coming from different directions with time sampling shorter than $1\mathrm{s}$. For this reason, the databases collected by a particular receiver contain information that can be used in analyses of local and global, short and long-term variations. Because of these properties, this type of remote sensing is used in studies of how many terrestrial and extraterrestrial phenomena influence the lower ionosphere and, consequently, the propagation of electromagnetic waves which can significantly be affected by the disturbed D-region [14,15,16,17,18,19,20,21].

There are several models for modeling the VLF/LF propagation in the Earth ionosphere waveguide, such as the Long-Wave Propagation Capability (LWPC) program [22], finite-difference time-domain (FDTD) method [23], coupled beams and effective complex impedance model [24], and Modefinder [25]. These models are used in many studies for determination of ionospheric parameters where characteristics of the considered area, the ionospheric state and properties of the analyzed disturbances affect the possibility of applying certain approximations. For example, during quiet conditions or during disturbances that do not affect the horizontal uniformity of the observed D-region it is possible to assume only altitude variations of the ionospheric plasma parameters, while, in the case of local disturbances caused by for example day-night transitions along the propagation path and lightnings, it is necessary to take into account both the vertical and horizontal variations of these parameters. The horizontal uniform ionosphere is analyzed in many papers using the LWPC and Modefinder models [10,26,27,28,29,30,31]. As an example, some localized perturbations of the ionosphere are considered in Reference [32]. FDTD method was used to model the day-night transitions along the propagation path (see, for example, Reference [23]). Effects of the geomagnetic field and its variations which can induce the need to include gyrotropy and anisotropy into account are most important in analyses of the high-latitude lower ionosphere, while, in the mid-latitude areas, effects of variations in the geomagnetic field should be taken into account during large geophysical disturbances of the Lithosphere-Atmosphere-Ionosphere-Magnetosphere system caused by large magnetic storms, hurricanes, etc. [24]. In this paper, we present a model of the daytime D-region parameters under quiet conditions which is based on data recorded in ionospheric remote sensing by VLF/LF signals and LWPC program that simulates their propagation. The chosen time period, in absence of local intensive geophysical disturbances (induced by, for example, solar terminator, lightnings, and hurricanes) which are followed by significant anisotropy, allows us to assume a horizontally uniform ionosphere. In addition, we consider mid- and low-latitude domains where influence of the magnetic field variations on the considered signals (the presented model is relevant for not too long propagation paths of VLF/LF signals which are reflected at altitudes below 76 km) is not significant under quiet conditions. To calculate the quiet D-region parameters, we also include into the consideration the analysis of disturbances induced by solar X-ray flares during the mid-day period when the indicated approximations are also justified and already used in many previous studies [10,26,27,28,29,30,31]. This is possible because solar X-ray flares do not cause local disturbances and induce practically horizontally uniform perturbations, especially within not too large areas, during the mid-day period.

Modeling of the solar X-ray flare perturbed D-region based on data obtained in its remote sensing by the VLF/LF signals assumes two approximations: (1) the lower ionosphere is usually considered as a horizontal uniform medium, and (2) the parameters in quiet conditions are considered as known quantity in which values are determined in previous statistical studies that, generally, do not represent the considered periods and areas. As we already said, the first approximation is good for a not too long propagation path of the considered signal and for daytime periods of a few hours around midday (this period depends on the season) in absence of intensive local disturbances. However, the second approximation can significantly affect the modeling, and this task was a subject of several studies which focused attention on the electron density and Wait’s parameters (the “sharpness” and signal reflection height). There are several methodologies used in these studies. They are based on the broad-band detection of radio atmospherics in periods of lightning activities and detection of the narrow-band VLF signals. A technique to measure the local mid-latitude daytime D-region parameters from the Earth-ionosphere waveguide mode interference pattern in spectra of radio atmospherics launched by lightning discharges, presented in Reference [33], is limited to periods of lightning activities. In the cases based on the analysis of narrow-band VLF signals, properties of modeling and necessary approximations which affect certainty of its applications strongly depend on geographical location of the considered transmitters and receivers. Namely, if the propagation path of the considered VLF signal is very long, as, for example, in the case of studies based on data recorded by receiver located in New Zealand from which transmitters are more than 10,000 $\mathrm{km}$ away [34,35,36], it is necessary to include changes in Wait’s parameters along the length of the path [34,35]. These changes provide additional possibilities for errors in modeling due to necessary approximations and changes in the ionosphere due to periodical and sudden events. Of course, increasing the propagation path length induces more effects of local disturbances which also affect the model certainty. Analyses of more receivers and transmitters can reduce these problems. A procedure for these ionospheric parameters modeling is given in Reference [37], where data for three signals recorded by six receivers are considered. In the mentioned studies, related to the considered areas, there are presented dependencies of the daytime Wait’s parameters on zenith angle during the solar maximum and minimum [34,35], on both zenith angle and local time [33], and dependencies of the signal reflection height on zenith angle for different seasons [35]. Expressions which provide dependencies of Wait’s parameters on more variables (zenith angle, season, smoothed sunspot number, latitude, and geomagnetic field) is presented in Reference [38]. However, the equations related to calculation of the signal reflection height cannot be applied to the newer sunspot datasets because one of these equations includes the Zürich sunspot number which refers to production of the sunspot number before 1981.

All these problems and the importance of determination of the quiet D-region parameters for many technologies motivate us to develop a model of the D-region which can be applied to shorter signal paths which significantly reduces disadvantages induced by the long distance signal propagation, and that includes the influences of:

• long-term variations (about 11 years) in solar radiations during solar cycle;
• seasonal variations (due to Earth’s revolution);
• daytime periodical changes; and
• sudden mid- and short-term influences

on the D-region properties. In other words, the aim of this study is to develop a procedure that will make it possible to take advantage of densely spaced VLF/LF transmitters and receivers, like those in Europe, to accurately model the D-region parameters in the area of interest and for the considered time period.

In this paper, we present the Quiet Ionospheric D-Region (QIonDR) model which provides a procedure for the determination of the D-region plasma parameters in quiet conditions using the VLF/LF observational data for the considered area in mid- and low-latitude domains, and the considered time period. The QIonDR model provides an analysis of the Wait’s parameters “sharpness” and signal reflection height. Determination of these parameters is important because knowing them allows computation of the D-region electron density N and, consequently, many other parameters, using different models [28,31,33,34,39,40]. As a result, in this study we also show the modeled electron density. To visualize the QIonDR model output, we apply it to data for the DHO and ICV signals emitted in Germany and Italy, respectively, and recorded in Serbia.

The article is organized as follows. The proposed methodology is presented in Section 2, while the analyses of observations and events are given in Section 3. Application of the QIonDR model on the DHO and ICV signals recorded in Belgrade is shown in Section 4, and conclusions of this study are given in Section 5.

2. Methodology

In this section, we describe a methodology for modeling Wait’s parameters ${\beta }_0$ and $H_0^{\prime }$ and the electron density $N_{\mathrm{e}0}$ in the quiet ionospheric D-region. This methodology is based on data obtained by the VLF/LF remote sensing of this atmospheric layer, using two VLF/LF signals, and the satellite X-ray flux data needed to determine the periods of ionospheric disturbances induced by solar X-ray flares.

To model propagation of the VLF/LF signal, we use the LWPC program. It models characteristics of the chosen signal considering its propagation in the Earth-ionosphere waveguide. Properties of the bottom boundary are based on the Westinghouse Geophysics Laboratory conductivity map [41], while the upper boundary is characterized by a conductivity that may be specified by the user. In this paper, we used Wait’s model of the ionosphere [42] which describes the horizontally homogeneous exponential conductivity profile by conductivity parameter ${\omega }_{\mathrm{r}}$:

$${\omega }_{\mathrm{r}}\left(h\right)={\omega }_0^2\left(h\right)/\mathsf{\nu }\left(h\right),$$

(1)

where ${\omega }_0\left(h\right)$ and $\mathsf{\nu }\left(h\right)$ are the electron plasma frequency and effective electron-neutral collision frequency, respectively. The first parameter can be obtained from the electron density $N_{\mathrm{e}}$ (${\omega }_0^2\left(h\right)\approx 3180N_{\mathrm{e}}$), while dependency of the collision frequency $\mathsf{\nu }$ on the altitude h is given by an approximative equation based on experimental data presented in References [43,44]:

$$\mathsf{\nu }\left(h\right)=1.82\times {10}^{11}{e}^{-0.15h},$$

(2)

Finally, according to the obtained vertical profiles of ${\omega }_{\mathrm{r}}$ shown in Reference [42], an approximative equation for this parameter is given in the following form:

$${\omega }_{\mathrm{r}}\left(h\right)=2.5\times {10}^5{e}^{\beta (h-H^{\prime })},$$

(3)

where the parameters $\beta$ and $H^{\prime }$ are known as Wait’s parameters and called “sharpness” and signal reflection height, respectively. These parameters are input parameters in the LWPC program. ${\omega }_{\mathrm{r}}$ is used for calculation of the reflection coefficient (the phase of the reflection coefficient is referred to the level where ${\omega }_{\mathrm{r}}=2.5\times {10}^5$ s${}^{-1}$) which is also dependent on the magnetic field. In Reference [42], it is assumed that the geomagnetic field is purely transverse. This approximation is possible because, for arbitrary directions of propagations, it has been indicated that transverse component of the geomagnetic field is most important for reflection of VLF radio waves at highly oblique incidence. Finally, the reflection coefficient is used in a mode theory calculations, which are described in Reference [42]. The output of LWPC program are the modeled amplitude and phase for input parameters and observed signal. Detailed descriptions of the LWPC and Wait’s models are given in References [22,42], while their application in the QIonDR model is described in detail in this Section.

Figure 1 shows the work-logic of the proposed methodology. It is split in the following two procedures related to the time period of the analysis of ionospheric parameters: (1) the Midday procedure (MDP), and (2) the Daytime procedure (DTP), detailed in Section 2.1 and Section 2.2, respectively.

2.1. Midday Periods

First, we analyze the changes in the midday ionospheric parameters induced by solar X-ray flares detected by the GOES satellite which occurred in midday periods. We process the recorded amplitudes and phases of both main and auxiliary VLF/LF signals in order to determine changes of these values at two different times during the solar X-ray flare influence with respect to their values before the disturbance (see Section 2.1.1). These changes are further used as input parameters in MDP (Section 2.1.2) which consists of two sub-procedures, first to determine Wait’s parameters before a solar X-ray flare, and second to estimate the dependency of these parameters on the solar cycle period and season at the midday. The first sub-procedure is further split in Sub-MDP-1a and Sub-MDP-1b, corresponding to the analyses of a signal s and a disturbed state i of an X-ray flare XF (XF in general is notation for particular flare; as an example see

Table 1. Dates, times, and classes of the considered X-ray flares, and zenith angles ${\theta }_{\mathrm{DHO}}$ and ${\theta }_{\mathrm{ICV}}$ for the latitude/longitude points of the middle propagation paths DHO-BEL and ICV-BEL, respectively. Differences of these angles, $\mathsf{\Delta }\theta$, are given in the last column. The positions of the considered VLF signal mid-paths, and corresponding angles ${\theta }_{\mathrm{DHO}}$, ${\theta }_{\mathrm{DHO}}$ and $\mathsf{\Delta }\theta$ are calculated using tools given at https://www.gpsvisualizer.com/calculators and https://www.esrl.noaa.gov/gmd/grad/solcalc/azel.html, respectively.

Flare XF	Date	Time (UT)	Flare Class	${\mathit{\theta }}_{\mathbf{DHO}}$(${}^{°}$)	${\mathit{\theta }}_{\mathbf{ICV}}$(${}^{°}$)	$\mathsf{\Delta }\mathit{\theta }$(${}^{°}$)
F1	5 May 2010	11:37	C8.8	33.79	27.88	5.91
F2	12 June 2010	09:20	C6.1	35.39	31.25	4.14
F3	3 November 2014	11:23	M2.2	64.84	58.61	6.23
F4	15 November 2014	11:40	M3.2	53.57	51.35	2.22
F5	6 January 2015	11:40	C9.7	72.05	65.76	6.29
F6	21 January 2015	11:32	C9.9	69.25	62.88	6.37
F7	29 January 2015	11:32	M2.1	53.07	50.65	2.42
F8	17 September 2015	09:34	M1.1	50.31	44.28	6.03
F9	14 May 2016	11:28	C7.4	37.50	35.31	2.19

), and the determination of Wait’s parameters in the quiet conditions before a solar X-ray flare XF, respectively. The output of Sub-MDP-1 consists of Wait’s parameters for all considered X-ray flares. Their values are further fitted in Sub-MDP-2 which provides two functions describing the dependencies of Wait’s parameters on the solar sunspot number and season. These two analytical expressions are the output of MDP, and they are used to model the daytime evolution of Wait’s parameters in DTP using the amplitude and phase of VLF/LF signals (Section 2.2).

2.1.1. VLF/LF Signal Processing

When an X-ray flare occurs, the main and auxiliary VLF/LF signals are processed, taking both the amplitude and phase, in order to detect changes with respect to their values in quiet conditions before an X-ray flare. Figure 2 shows an example of temporal evolutions of signals’ amplitude and phase, where their values in quiet and pertubed conditions are emphasized. These amplitude and phase values are needed in processing steps described in the following:

1

Determination of the amplitude ${\mathit{A}}_0^{\mathrm{XFs}}$ of signal $\mathit{s}$ in a quiet state before an X-ray flare XF. To find this value for both VLF/LF signals, we consider three time bins of length $\mathsf{\Delta }{t}_{\mathrm{bin}}$ (in our processing we use $\mathsf{\Delta }{t}_{\mathrm{bin}}=20$ s) within a time window of a few minutes before the signal perturbation. The amplitude $A_0^{\mathrm{XFs}}$ is defined as the minimum of median values of recorded amplitudes in each bin, while the maximal absolute deviation of the recorded amplitudes in the considered bins from the median value is used as a figure for its absolute error d$A_0^{\mathrm{XFs}}$. In the following, we use “d” for the absolute error and “$\mathsf{\Delta }$” to denote the difference between the amplitudes at two different times during the disturbance and quiet state.

2

Determination of the reference phase ${\mathit{P}}_{\mathrm{ref}}^{\mathrm{XFs}}$ of a signal $\mathit{s}$ during an X-ray flare XF. The recorded phase of a VLF/LF signal represents the phase deviation of the considered signal with respect to the phase generated at the receiver. For this reason, the recorded phase has a component of constant slope that should be removed. A linear fit is performed through five points, three before the signal perturbation and two at the end of the considered observation interval, is performed. Phase values at these points are determined in the same way as in the procedure for amplitude estimation as described in point 1). For each time bin $\mathsf{\Delta }t$, we compute the median value of phase samples. Furthermore, the largest deviation of phase values within each bin is used to estimate the absolute error d$P_{\mathrm{ref}}^{\mathrm{XFs}}$ of the reference phase.

It is worth noting that disturbances induced by a solar X-ray flare can last from several tenth of minutes to over one hour. For this reason, quiet conditions can be different before and after disturbances. In addition, it is possible that some sudden events or some technical problem affect at least one signal in a time interval starting after the one used in this study. For instance, in Figure 2, we show a visible increase in the “quiet” visible increase in the “quiet” phase of about 15${}^{°}$ and 5${}^{°}$ for the DHO and ICV signals, respectively.

3

Determination of differences in the amplitude $\mathsf{\Delta }{\mathit{A}}^{\mathrm{XFsi}}$ and phase $\mathsf{\Delta }{\mathit{P}}^{\mathrm{XFsi}}$ of the signal $\mathit{s}$ during a disturbance induced by a solar X-ray flare XF in state $\mathit{i}$ with respect to quiet conditions. To avoid any dependence of results on the selection of time, we perform twice the analysis of changes in the signal parameters with respect to the initial, unperturbed state, by selecting two different times which are emphasized by vertical dashed and dotted lines in right panels in Figure 2 displaying time evolutions of the amplitude ($\mathsf{\Delta }{A}^{\mathrm{XFsi}}=A^{\mathrm{XFs}}\left(t_{\mathrm{i}}\right)-A_0^{\mathrm{XFs}}$) and phase ($\mathsf{\Delta }{P}^{\mathrm{XFsi}}=P^{\mathrm{XFs}}\left(t_{\mathrm{i}}\right)-P_{\mathrm{ref}}^{\mathrm{XFs}}\left(t\right)$) changes for both signals during the disturbance induced by the solar X-ray flare occurred on 17 September 2015.

The absolute errors d$A^{\mathrm{XFs}1}$ and absolute errors d$A^{\mathrm{XFs}2}$ of amplitudes $A^{\mathrm{XFs}1}$ and $A^{\mathrm{XFs}2}$, and d$P^{\mathrm{XFs}1}$ and d$P^{\mathrm{XFs}2}$ of phases $P^{\mathrm{XFs}1}$ and $P^{\mathrm{XFs}2}$, respectively, are determined as for the quiet state, i.e.: (1) we calculate $A^{\mathrm{XFs}1}$, $A^{\mathrm{XFs}2}$, $P^{\mathrm{XFs}1}$ and $P^{\mathrm{XFs}2}$ as median values in two bins of width $\mathsf{\Delta }{t}_{\mathrm{bin}}=20$ s around times $t_1$ and $t_2$; (2) we define absolute errors d$A^{\mathrm{XFs}1}$ and d$A^{\mathrm{XFs}2}$, and d$P^{\mathrm{XFs}1}$ and d$P^{\mathrm{XFs}2}$ in terms of maximal absolute deviations of the corresponding quantities within the bins. The total absolute errors are obtained as follows:

$$\mathrm{d}\left(\mathsf{\Delta }{A}^{\mathrm{XFsi}}\right)=\mathrm{d}{A}_0^{\mathrm{XFs}}+\mathrm{d}{A}^{\mathrm{XFsi}},$$

(4)

$$\mathrm{d}\left(\mathsf{\Delta }{P}^{\mathrm{XFsi}}\right)=\mathrm{d}{P}_{\mathrm{ref}}^{\mathrm{XFs}}+\mathrm{d}{P}^{\mathrm{XFsi}}.$$

(5)

where $i=\{1,2\}$.

As a result of the above processing, the changes in amplitude and phase at the two times during the disturbance are obtained with respect to their values in quiet conditions.

2.1.2. Modeling

As shown in Figure 1, the procedure for modeling Wait’s parameters describing the quiet conditions in midday periods (denoted with MDP in Figure 1) is split into two sub-procedures that provides estimations of: (1) their values for a particular event, and (2) their dependencies on the solar cycle period, described in terms of smoothed daily sunspot number $\sigma$, and season parameter $\chi =\mathrm{DOY}/365$, where DOY is the day of year. Here, we approximate the tropical year lasting 365 days (instead 365.24255 days).

Sub-MDP-1: 

Estimation of Wait’s parameters in quiet conditions before a solar X-ray flare. As can be seen in Figure 1 this procedure consists of two following sub-procedures:

• Sub-MDP-1a. This sub-procedure provides values of Wait’s parameters in the quiet ionosphere for which the amplitude $\mathsf{\Delta }{A}_{\mathrm{mod}}^{\mathrm{sqd}}$ and phase $\mathsf{\Delta }{P}_{\mathrm{mod}}^{\mathrm{sqd}}$ changes are similar to the corresponding recorded values, $\mathsf{\Delta }{A}^{\mathrm{XFsi}}$ and $\mathsf{\Delta }{P}^{\mathrm{XFsi}}$, respectively. It is based on determination of changes in two sets of the modeled amplitude $\mathsf{\Delta }{A}_{\mathrm{mod}}^{\mathrm{sqd}}=A_{\mathrm{mod}}^{\mathrm{sd}}-A_{\mathrm{mod}}^{\mathrm{sq}}$ and phase $\mathsf{\Delta }{P}_{\mathrm{mod}}^{\mathrm{sqd}}=P_{\mathrm{mod}}^{\mathrm{sd}}-P_{\mathrm{mod}}^{\mathrm{sq}}$ of the signal s, and their deviations from the corresponding recorded values $\mathsf{\Delta }{A}^{\mathrm{XFsi}}$ and $\mathsf{\Delta }{P}^{\mathrm{XFsi}}$ for the signal s and disturbed state i. These sets, representing the modeled quiet and disturbed states, q and d, respectively, are performed in simulations of the considered VLF/LF signal propagation using LWPC numerical model developed by the Space and Naval Warfare Systems Center, San Diego, CA, USA [22]. The input parameters of this numerical model are Wait’s parameters “sharpness” and signal reflection height, while the modeled amplitude and phase are its output (see the diagram in Figure 3).
  According to the results presented in literature (see References [26,27,31,33,34,35]), Wait’s parameters can be considered within intervals 0.2 km${}^{-1}$–0.6 km${}^{-1}$ for $\beta$, and 55 km–76 km for $H^{\prime }$, where the quiet conditions can be described within intervals 0.2 km${}^{-1}$–0.45 km${}^{-1}$ for ${\beta }^{\mathrm{q}}$, and 68 km–76 km for ${H^{\prime }}^{\mathrm{q}}$. To model the parameter values representing a disturbed state d, ${\beta }^{\mathrm{d}}$ and ${H^{\prime }}^{\mathrm{d}}$, given those describing a quiet state q, we use conditions ${\beta }^{\mathrm{q}}<{\beta }^{\mathrm{d}}$ and ${H^{\prime }}^{\mathrm{q}}>{H^{\prime }}^{\mathrm{d}}$ which are based on many studies [26,27,31]. In the following, we use these intervals with steps of 0.01 km${}^{-1}$ and 0.1 km, respectively, as input in the LWPC numerical program.
  The first output of the Sub-MDP-1a are the pairs of Wait’s parameters referring to the quiet state before a solar X-ray flare XF $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ for which the LWPC model can calculate the amplitude and phase differences for both main (m) and auxiliary (a) signals ($s=m,a$) and for both disturbed state ($i=1,2$) that satisfy the conditions:

  $$\mathrm{d}\left(\mathsf{\Delta }{A}_{\mathrm{mod}}^{\mathrm{XFsiqd}}\right)=\mathrm{abs}(\mathsf{\Delta }{A}_{\mathrm{mod}}^{\mathrm{sqd}}-\mathsf{\Delta }{A}^{\mathrm{XFsi}})<\mathrm{d}\left(\mathsf{\Delta }{A}^{\mathrm{XFsi}}\right),\mathrm{and}$$

  (6)

  $$\mathrm{d}\left(\mathsf{\Delta }{P}_{\mathrm{mod}}^{\mathrm{XFsiqd}}\right)=\mathrm{abs}(\mathsf{\Delta }{P}_{\mathrm{mod}}^{\mathrm{sqd}}-\mathsf{\Delta }{P}^{\mathrm{XFsi}})<\mathrm{d}\left(\mathsf{\Delta }{P}^{\mathrm{XFsi}}\right),$$

  (7)

  where $\mathrm{d}\left(\mathsf{\Delta }{A}^{\mathrm{XFsi}}\right)$ and $\mathrm{d}\left(\mathsf{\Delta }{P}^{\mathrm{XFsi}}\right)$ are the absolute errors in the recorded signal characteristics.
  The second output of Sub-MDP-1a are errors in modeling, e.g., the absolute deviations of the modeled changes in the amplitude and phase from their recorded values: $\mathrm{d}\left(\mathsf{\Delta }{A}_{\mathrm{mod}}^{\mathrm{XFsiqd}}\right)$ and $\mathrm{d}\left(\mathsf{\Delta }{P}_{\mathrm{mod}}^{\mathrm{XFsiqd}}\right)$. Both outputs are used in Sub-MDP-1b.
• Sub-MDP-1b. The goal of this sub-procedure is to find the pair of Wait’s parameters $({\beta }_0^{\mathrm{XFmidday}}$,${H^{\prime }}_0^{\mathrm{XFmidday}})$, from those $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ extracted in Sub-MDP-1a, which provides the best agreement between the modeled and measured amplitude and phase changes of the VLF/LF signals. To do that, we analyze both the observation and modeling absolute errors, i.e., $\mathrm{d}\left(\mathsf{\Delta }{A}^{\mathrm{XFsi}}\right)$ and $\mathrm{d}\left(\mathsf{\Delta }{P}^{\mathrm{XFsi}}\right)$, for observations and $\mathrm{d}\left(\mathsf{\Delta }{A}_{\mathrm{mod}}^{\mathrm{XFsiqd}}\right)$ and $\mathrm{d}\left(\mathsf{\Delta }{P}_{\mathrm{mod}}^{\mathrm{XFsiqd}}\right)$ for modeling. These values are used to quantify the observed $w_{\mathrm{obs}}^{\mathrm{XF}}$ and modeled $w_{\mathrm{mod}}^{\mathrm{XFq}}$ weights for each extracted pair of Wait’s parameters. Details about the estimations of these weights are provided in Appendix A, while an example of representation of the extracted pairs in the 2D Wait’s parameter space is shown in the left panel of Figure 4. Each pair of Wait’s parameters is represented as a point. The color of points describes their observation and modeling precisions. To find points (i.e., pairs of Wait’s parameters) which best model the amplitude and phase changes, the region around each candidate point is analyzed as follows. The weight of each point, describing the overall observation and modeling precisions, is computed as the product of observed and modeled weights, i.e., $w_{\mathrm{obs}}^{\mathrm{XF}}{w}_{\mathrm{mod}}^{\mathrm{XFq}}$.
  Furthermore, the weight $w_{\mathrm{n}}^{\mathrm{XFq}}$ is introduced to quantify the influence of each point within the region around the candidate point. This weight is defined as

  $$w_{\mathrm{n}}^{\mathrm{XFq}}={\mathsf{\Sigma }}_{\mathrm{k}}\left\{\frac{1}{n^{\mathrm{qk}}}{w}_{\mathrm{obs}}^{\mathrm{XFk}}{w}_{\mathrm{mod}}^{\mathrm{XFk}}\right\},$$

  (8)

  where $n^{\mathrm{qk}}$ is the distance between the quiet states q and k which refer to pairs $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ and $({\beta }^{\mathrm{XFk}},{H^{\prime }}^{\mathrm{XFk}})$, respectively.
  The total weight $w_{\mathrm{tot}}^{\mathrm{XFq}}$ for the pair $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ is computed as:

  $$w_{\mathrm{tot}}^{\mathrm{XFq}}=w_{\mathrm{obs}}^{\mathrm{XFq}}{w}_{\mathrm{mod}}^{\mathrm{XFq}}+w_{\mathrm{n}}^{\mathrm{XFq}}.$$

  (9)
  Finally, the pair of Wait’s parameters $({\beta }_0^{\mathrm{XFmidday}},{H^{\prime }}_0^{\mathrm{XFmidday}})$ describing the quiet D-region before a solar X-ray flare XF, which provides the best agreement of the considered modeled and observed amplitude and phase changes, is obtained as the pair with the largest total weight $W_{\mathrm{tot}}^{\mathrm{XF}}={\max }_{\mathrm{q}}\left\{w_{\mathrm{tot}}^{\mathrm{XFq}}\right\}$. The estimation errors $[e{\beta }_{0-}^{\mathrm{XF}},e{\beta }_{0+}^{\mathrm{XF}}]$ and $[{e{H}^{\prime }}_{0-}^{\mathrm{XF}},{e{H}^{\prime }}_{0+}^{\mathrm{XF}}]$ of these parameters are obtained from distribution of pairs $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ which satisfy conditions (6) and (7). For instance, the error for ${\beta }_0^{\mathrm{XFmidday}}$ are computed as follows. For the pair $({\beta }_0^{\mathrm{XFmidday}},{H^{\prime }}_0^{\mathrm{XFmidday}})$ represented by green diamonds in Figure 4, the interval $[e{\beta }_{0-}^{\mathrm{XF}},e{\beta }_{0+}^{\mathrm{XF}}]$ is estimated by taking the smaller and larger values of ${\beta }^{\mathrm{XFq}}$ estimates, for the given ${H^{\prime }}_0^{\mathrm{XFmidday}}$. In the same way, we estimate the error for ${H^{\prime }}_0^{\mathrm{XFmidday}}$.

Sub-MDP-2: 

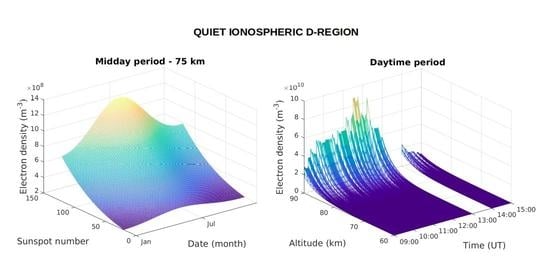
Modeling of Wait’s parameters in terms of sunspot number and season. The aim of this subroutine is to model the behaviour of Wait’s parameters by fitting the $({{\beta }_0}^{\mathrm{XFmidday}},{H^{\prime }}_0^{\mathrm{XFmidday}})$ pair. This requires a deeper understanding of the X-ray influences on the D-region. During quiet conditions, the solar hydrogen Ly$\alpha$ radiation has a dominant influence on ionization processes in the ionospheric D-region (see, for example, Reference [45]). The intensity of this radiation varies periodically during the solar cycle and its variation depends on the sunspot number. Because of that, we use the smoothed daily sunspot number $\sigma$ to represent the intensity of the incoming solar radiation in the Earth’s atmosphere. The intensity of this radiation decreases with the solar zenith angle due to larger attenuations in the atmosphere above the considered locations. Generally, the zenith angle changes are due to seasonal and‘daily variations. However, this study focuses on time intervals around middays which allows us to assume that the seasonal changes represent the zenith angle variations. We introduce the seasonal parameter $\chi =\mathrm{DOY}/365$ where DOY is the day of year. This parameter has values between 0 and 1. Some authors report on possible influences of the geomagnetic field on the Wait’s parameter [38,46]. However, this is is more pronounced at polar and near polar areas due to shapes of geomagnetic lines that allows charge particle influences on the ionospheric properties. As this study is focused on the low and mid latitude ionosphere, we neglect these effects.

Dependencies of Wait’s parameters at midday on solar cycle and seasonal variations can be given as functions:

$${\beta }_0^{\mathrm{midday}}=f(\sigma ,\chi )$$

(10)

and

$${H_0^{\prime }}^{\mathrm{midday}}=g(\sigma ,\chi ).$$

(11)

These relations are not general and have yet to be determined for the location of interest and the time to which the recorded data refer to.

The knowledge of these functions allow us to calculate the vertical distribution of the Wait’s horizontally uniform ionosphere, $N_{\mathrm{e}0}(h,\sigma ,\chi )$, using the equation given in Reference [34] for different values of $\sigma$ and $\chi$:

$${\displaystyle N_{\mathrm{e}0}^{\mathrm{midday}}(\sigma ,\chi ,h)=1.43·{10}^{13}{e}^{-{\beta }^{\mathrm{midday}}(\sigma ,\chi )H^{\prime }{}^{\mathrm{midday}}(\sigma ,\chi )}{e}^{[{\beta }^{\mathrm{midday}}(\sigma ,\chi )-0.15]h},}$$

(12)

where $N_{\mathrm{e}0}^{\mathrm{midday}}$ and ${\beta }^{\mathrm{midday}}$ are given in m${}^{-3}$ and km${}^{-1}$, respectively, and $H^{\prime }$ and altitude h are given in km. This equation was used to determine the temporal ($H_0^{\prime }(t,h)$) and energy ($H_0^{\prime }(ϵ,h)$) distributions of the D-region electron density perturbed by a solar X-ray flare (see, for example, References [31,47,48]).

2.2. Daytime Variations of Ionospheric Parameters

The determination of the daytime variation of Wait’s parameters and electron density is based on the comparison of observational and modeling data as for the analysis of midday variations. However, the DTP procedure considers only one VLF/LF signal, e.g., the main one. The reason for that is that the approximation of a horizontally uniform ionosphere during the entire daytime period (far from the sunrise and sunset) can be used when the size of the observed area corresponds to a relatively short propagation path of the signal.

2.2.1. VLF/LF Signal Processing

The goal of this procedure is to find the amplitude and phase variations relative to their values in the midday period. We consider data recorded during the daytime period, far from the sunrise and sunset. The midday period is estimated from tendency of the amplitude time evolution $A\left(t\right)$. Namely, it rises until the midday and decreases afterwards which allows us to assume the period around the amplitude maximum as the midday period. The duration of this period is a few minutes and it depends on the season and possible existence of unperiodical disturbances which should be excluded from the analysis.

To exclude the short-term amplitude picks that do not represent periodic daily variations, the midday amplitude $A^{\mathrm{midday}}$ is estimated as the median amplitude value in the midday period.

Similarly to the analysis in Section 2.1.1, the time evolution of the phase is determined by estimating the linear phase trend obtained by interpolation of phase values estimated within time bins in quiet conditions. The midday phase $P^{\mathrm{midday}}$ is estimated from the obtained phase evolution P(t) in the same way like for the midday amplitude.

The final step of this processing is the calculation of amplitude and phase deviations from their reference values, i.e., $\mathsf{\Delta }A=A-A^{\mathrm{midday}}$ and $\mathsf{\Delta }P=P-P^{\mathrm{midday}}$.

2.2.2. Modeling

The modeling of daytime temporal evolution of Wait’s parameters is based on comparison of deviation of observational and modeled changes with respect to their midday values. The modeled midday values $A_{\mathrm{mod}}^{\mathrm{midday}}$ and $P_{\mathrm{mod}}^{\mathrm{midday}}$ are obtained from ${\beta }_0^{\mathrm{midday}}$ and $H_0^{\prime }$, while the modeled amplitude $A_{\mathrm{mod}}$ and phase $P_{\mathrm{mod}}$ are outputs of the LWPC program for the given pair of Wait’s parameters. Wait’s parameters ($\beta \left(t\right),H^{\prime }\left(t\right)$) at time t are estimated as those that best satisfy the conditions

$$A-A^{\mathrm{midday}}=A_{\mathrm{mod}}-A_{\mathrm{mod}}^{\mathrm{midday}}$$

(13)

and

$$P-P^{\mathrm{midday}}=P_{\mathrm{mod}}-P_{\mathrm{mod}}^{\mathrm{midday}}.$$

(14)

Finally, the electron density $N_{\mathrm{e}0}(t,\sigma ,\chi )$ is obtained from Equation (15):

$${\displaystyle N_{\mathrm{e}0}(t,h,\sigma ,\chi )=1.43·{10}^{13}{e}^{-\beta (t,\sigma ,\chi )H^{\prime }(t,\sigma ,\chi )}{e}^{\left(\beta \right(t,\sigma ,\chi )-0.15)h},}$$

(15)

where the parameters are given in the same units as in Equation (12).

3. Studied Area and Considered Events

To give an example of this model application, we apply it to data recorded in Belgrade in the lower ionosphere observations by the VLF signals emitted in Germany and Italy, while the information of the X-ray flares occurrences was taken from the website https://hesperia.gsfc.nasa.gov/goes/goes_event_listings/. For a better understanding of the presented procedure, we will first describe observations and then (in Section 4) we present the application of the model to the observed data.

3.1. Remote Sensing of Lower Ionosphere

The lower ionosphere observations are performed by two VLF signals of frequencies 23.4 kHz and 20.27 kHz emitted by the DHO transmitter in Germany (Rhauderfehn, 53.08 N, 7.61 E) and the ICV transmitter in Italy (Isola di Tavolara, 40.92 N, 9.73 E), respectively. Amplitudes and phases of these signals are recorded by the AWESOME (Atmospheric Weather Electromagnetic System for Observation Modeling and Education) receiver [49] located in Belgrade, Serbia, which was a part of the Stanford/AWESOME Collaboration for Global VLF Research (http://waldo.world/narrowband-data/). The locations of the considered transmitters and receiver, as well as the propagation paths, are shown in Figure 5.

The best properties of the recorded VLF/LF signals in the Belgrade receiver station are those of the DHO signal. That can be explained by a not too long propagation path and a large emitted power (800 kW). This is why the DHO signal is used in many studies based on data collected by the Belgrade receiver station (see, for example, References [10,50]). Although the distance between the Italian transmitter and Belgrade receiver is shorter than the path in the first case, its emitted power is 40 times lower than that of the signal emitted in Germany. For this reason, we rank the DHO and ICV signals as the main and auxiliary ones, respectively.

3.2. Considered X-ray Flares

As one can see in Section 2, the presented model assumes a horizontally uniform Wait’s ionosphere [42] for the area where both signals propagate. That assumption requires analyses of the time period when solar influences is similar above the considered part of Europe, e.g., periods around the midday. In addition, modeling of the electron density by the procedure given in Reference [34] is more appropriate for not too intensive flares. For this reason, we consider flares of up to class M5 (like in Reference [10]). Due to absence or insignificant ionospheric disturbances induced by low intensive flares, we consider events of classes larger than C5.0. In our collected database, we find 9 not too intensive events for which the differences in solar zenith angles, $\mathsf{\Delta }\theta ={\theta }_{\mathrm{DHO}}-{\theta }_{\mathrm{ICV}}$ (calculated using the website https://www.esrl.noaa.gov/gmd/grad/solcalc/azel.html for the latitude/longitude points of the middle propagation paths DHO-BEL (49.28 N, 14.00 E) and ICV-BEL (42.81 N, 15.06 E), obtained in calculations by the program given at the website https://www.gpsvisualizer.com/calculators) satisfy the first mentioned condition. As one can see in Table 1, classes of the considered flares are between C6.1 and M3.2, while differences in the solar zenith angles of the DHO and ICV signal mid-paths, ${\theta }_{\mathrm{DHO}}$ and ${\theta }_{\mathrm{ICV}}$, respectively, are lower than 6.4${}^{°}$.

4. Results and Discussion

The proposed methodology is applied to data obtained in observations described in Section 3. Here, we present the results of:

1

Modeling the ionospheric parameters in midday periods over the part of Europe included within the location of transmitted signals (Sardinia, Italy, for the ICV signal) and (Lower Saxony, Germany for the DHO signal) and the receiver in Belgrade, Serbia, with respect to the daily smoothed sunspot number and season. This part consists of the following steps:

• Modeling of pairs of Wait’s parameters which satisfy conditions given by Equations (6) and (7) by the LWPC numerical program and determination pair (${{\beta }_0}^{\mathrm{XF}},H_0^{\prime }{}^{\mathrm{XF}}$) that provides the best fit of observational data for the considered X-ray flares.
• Determination of dependencies of the midday Wait’s parameters, ${{\beta }_0}^{\mathrm{midday}}$ and $H_0^{\prime }{}^{\mathrm{midday}}$, and the electron density, $N^{\mathrm{midday}}$, from parameters that describe the solar activity and Earth’s motion: the smoothed daily sunspot number $\sigma$, and parameter $\chi$ describing seasonal variations.

2

Modeling of daytime variations of ionospheric parameters for a particular day. This procedure consists of:

• Modeling of time evolutions of Wait’s parameters from comparisons of the recorded and modeled amplitude and phase changes with respect to their values in the midday.
• Modeling of the electron density time evolution for the D-region heights during daytime.

For both analyses, it is necessary to know the modeled amplitude and phase of the considered signals. For this reason, we first present the description of their determination.

4.1. Modeling of the DHO and ICV Signal Amplitudes and Phases by the LWPC Numerical Program

As noticed in Section 2, the LWPC program simulates propagation of the VLF and LF signals from a particular transmitter to a particular receiver of these waves. Wait’s parameters, the “sharpness” $\beta$ and signal reflection height $H^{\prime }$ are the input values for this program, while the modeled amplitude $A_{\mathrm{mod}}$ and phase $P_{\mathrm{mod}}$ are its outputs. In this study, we perform analysis for input values of $\beta$ and $H^{\prime }$ in domains 0.2 km${}^{-1}$–0.6 km${}^{-1}$ and 55 km–76 km, respectively, with corresponding steps of 0.01 km${}^{-1}$ and 0.1 km.

Results of modeling by the LWPC program for location of the Belgrade receiver and the DHO and ICV transmitters are shown in Figure 6. Here, it is important to pay attention to the fact that these panels represent the modeled amplitudes and phases (within the domain from −180${}^{\circ }$ to 180${}^{\circ }$), while the procedure for comparison of recorded and modeled signal characteristics, described in Section 2.1.2, requires changes of these values in the disturbed with respect to quiet conditions. The dependencies of these changes on the input Wait’s parameters have the same distributions as the presented corresponding graphs because they have lower than those modeled by the LWPC program for a constant value of modeled amplitude or phase in quiet conditions.

As one can see in Figure 6, there is no unique pair of Wait’s parameters that produce specific LWPC output values. That is why only one presented panel, even though the modeled amplitude/phase in quiet conditions are given, it cannot be used for determination of the input pair that provides the best fit of the observed data. The fact that it is impossible to determine a unique combination of Wait’s parameters from a single value of signal characteristic was noticed by other authors (see, e.g., Reference [36]).

4.2. Midday Values—Solar Cycle and Seasonal Variations

The procedure for determination of the considered midday values during the solar cycle and year consists of two parts:

• Determination of pairs $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ which describe quiet states before the considered X-ray flares (Section 4.2.1).
• Determination of dependencies of Wait’s parameters and the electron density in midday quiet conditions on $\sigma$ and $\chi$ (Section 4.2.2).

4.2.1. Determination of Pairs $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$

Comparison of the recorded and modeled changes in amplitude and phase of the DHO and ICV signals using the procedure described in Section 2.1.2 gives pairs of Wait parameters $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ which satisfy the conditions given by Equations (6) and (7). These values are presented for all considered events in Figure 7. To better visualize the precision in comparisons, we divide the extracted pairs in ten categories depending on relative errors in modeling of both amplitude and phase of the DHO and ICV signals. The category c = 1, 2, 3, ..., 10 indicates that all relative errors defined by Equation (A1) for pairs $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ have values less than $c·10\%$. The values of $({\beta }^{\mathrm{XFq}},{H^{\prime }}^{\mathrm{XFq}})$ which have the largest total weight calculated by Equation (9), e.i. values $({\beta }_0^{\mathrm{XFmidday}},{H^{\prime }}_0^{\mathrm{XFmidday}})$ for a X-ray flare XF, are indicated by green diamonds.

According the number of neighbors (see Figure 7) that also satisfy the conditions given by Equations (6) and (7), stability of the obtained pairs (${\beta }_0^{\mathrm{XFmidday}}$ and ${H^{\prime }}_0^{\mathrm{XFmidday}})$ is good in 8 out of 9 cases. It can be also seen in

Table 2. The obtained Wait’s parameters “sharpness”, ${\beta }_0^{\mathrm{XFmidday}}$, and signal reflection height, ${H^{\prime }}_0^{\mathrm{XFmidday}}$, and domains of their possible deviations going to larger ($e{\beta }_{0+}^{\mathrm{XF}}$ and $e{H^{\prime }}_{0+}^{\mathrm{XF}}$) and lower values ($e{\beta }_{0-}^{\mathrm{XF}}$ and $e{H^{\prime }}_{0-}^{\mathrm{XF}}$) for the considered flares. The last three columns show weights $W_{\mathrm{tot}}^{\mathrm{XF}}$ of the determined pairs of Wait’s parameters (${\beta }_0^{\mathrm{XFmidday}}$, ${H^{\prime }}_0^{\mathrm{XFmidday}})$, smoothed daily sunspot number $\sigma$, and seasonal parameter $\chi$.

Flare XF	${\mathit{\beta }}_0^{\mathbf{XFmidday}}$	${{\mathit{H}}^{\prime }}_0^{\mathbf{XFmidday}}$	$\mathit{e}{\mathit{\beta }}_{0+}^{\mathbf{XF}}$	$\mathit{e}{\mathit{\beta }}_{0-}^{\mathbf{XF}}$	${{\mathit{eH}}^{\prime }}_{0+}^{\mathbf{XF}}$	${{\mathit{eH}}^{\prime }}_{0-}^{\mathbf{XF}}$	${\mathit{W}}_{\mathbf{tot}}$	$\mathit{\sigma }$	$\mathit{\chi }$
No	(km${}^{-1}$)	(km)	(km${}^{-1}$)	(km${}^{-1}$)	(km)	(km)
F1	0.31	74.7	0.01	0.04	0.5	1.4	104.0	10.7	0.3452
F2	0.31	74.8	0.08	0.06	1.2	2.6	103.5	23.1	0.4493
F3	0.42	74.2	0.03	0.03	0.3	0.2	5.6	100.5	0.8438
F4	0.41	74.0	0.04	0.05	0.9	0.9	154.5	100.1	0.8767
F5	0.43	72.4	0.02	0.03	0.7	0.9	29.7	112.6	0.0164
F6	0.42	71.5	0.01	0.03	0.2	0.5	56.8	87.6	0.0575
F7	0.45	70.2	0.00	0.02	0.1	0.1	1.4	84.8	0.0795
F8	0.34	71.9	0.04	0.04	1.1	1.0	115.9	54.0	0.7151
F9	0.42	70.7	0.03	0.06	3.6	1.0	111.5	68.6	0.3699

showing the relevant domains with higher $e{\beta }_{0+}^{\mathrm{XF}}$ and $e{H}_{0+}^{\prime }{}^{\mathrm{XF}}$, and lower $e{\beta }_{0-}^{\mathrm{XF}}$ and $e{H}_{0-}^{\prime }{}^{\mathrm{XF}}$ values of Wait’s parameters with respect to ${\beta }_0^{\mathrm{XFmidday}}$ and ${H^{\prime }}_0^{\mathrm{XFmidday}}$ (for fixed other parameter), respectively. Visualization by different scatters shows that 6 cases have the highest precision of modeling for $c=1$, while the lowest precision occurs for $c=3$. The weights $W_{\mathrm{tot}}^{\mathrm{XF}}$, calculated by Equation (9) and given in Table 2, show large differences for the considered events (from 1.4 to 154.5).

4.2.2. Wait’s Parameters and Electron Density in Quiet Conditions

The final step in determination of midday Wait’s parameters is analysis of their dependencies on daily smoothed solar sunspot number $\sigma$ and seasonal variations described by parameter $\chi$. To better visualize the difference due to larger solar radiation in the period around the maximum of the solar cycle than in the period around its minimum, we show the relevant points in Figure 8 with a filled and open scatters, respectively. Different seasons are described with blue (winter), green (spring), yellow (summer), and red (autumn) scatters.

Dependencies of the midday Wait’s parameters on the solar sunspot number are shown in the left panels of Figure 8. Here, we consider the smoothed sunspot number (over 21 days) and take the value for the period of 20 days before and the considered day from the database given at http://sidc.oma.be/silso/datafiles. The upper panel indicates the increase of the parameter $\beta$ with $\sigma$, while decrease of the signal reflection height with $\sigma$ is clearly shown in the bottom panel. These tendencies are in agreement with previous studies of Wait’s parameters during solar X-ray flares where the increase/decrease of the “sharpness”/signal reflection height with the electron density is reported (see, for example, Reference [31]). In this case, the rise of the D-region electron density is a consequence of the Ly$\alpha$ radiation increase in approaching the solar cycle maximum. In fitting of these dependencies, we assume polynomial functions of the orders 2 and 1, respectively, which is by one order of magnitude larger than in Reference [38] where the dependency of the parameter $\beta$ is given as a linear function of the sunspot number, while variation of $H^{\prime }$ with the sunspot number is not suggested. As one can see in the right panels in Figure 8, the seasonal variation is more complex than in the previous case. However, if two scatters related to the solar cycle minimum are excluded we can see approximative sinusoidal shapes in both cases. For this reason, we assume sinusoidal dependencies of Wait’s parameters on parameter $\chi$ similarly as in Reference [38] but with daily (instead of monthly) changes and additional phase shifts which provide maximum/minimum values of $\beta$/H’ for the summer solstice when the expected radiation coming in the considered area reaches its annual maximum.

Tow-dimensional fittings of Wait’s parameters yield the following expressions:

$${\beta }_0^{\mathrm{midday}}=0.2635+0.002573·\sigma -9.024·{10}^{-6}{\sigma }^2+0.005351·\cos \left(2\mathsf{\pi }(\chi -0.4712)\right)$$

(16)

and

$${H_0^{\prime }}^{\mathrm{midday}}=74.74-0.02984·\sigma +0.5705·\cos (2\mathsf{\pi }(\chi -0.4712)+\mathsf{\pi }),$$

(17)

which provides good agreement of the computed Wait’s parameters with their modeled values given in Table 1. The maximum differences of their values are less than 0.04 km${}^{-1}$, and 2.5 km. These values are in good agreement with those obtained in Reference [51] for the night-time Wait’s parameters and they are similar to the maximum “errors” given in Table 2. Wait’s parameters are visualized in Figure 9 for ${\beta }_0$ (left panel) and $H_0^{\prime }$ (right panel). The obtained values lie in domains 0.31 km${}^{-1}$–0.45 km${}^{-1}$ and 70.6 km–74.7 km, respectively. An increase/decrease in dependencies of the “sharpness”/reflection height with $\sigma$ is visible during the whole year. The minimum/maximum values of ${\beta }_0/H_0^{\prime }$ for the same $\sigma$ are reached during the summer solstice when the solar radiation has the greatest impact on the ionosphere.

Introduction of Equations (16) and (17) in Equation (12) gives the midday electron density from $\sigma$ and $\chi$ at altitude h. These dependencies at 70 km, 75 km, and 80 km are shown in Figure 10.

As one can see, variations are more visible at larger heights and can reach values near ${10}^{10}$ m${}^{-3}$ at 80 km for periods with large number of solar sunspot number. Due to the most intensive influences of solar radiation, the electron density has largest values during the summer solstice.

4.3. Daytime Variations

Knowing the midday Waits parameters allows us to calculate their time evolutions during a quiet day. Here, we present an example using the DHO signal amplitude and phase recorded by the Belgrade VLF receiver on 6 September 2014 (DOY = 250; $\chi$ = 0.6849) in which deviations, $\mathsf{\Delta }A$ and $\mathsf{\Delta }P$, from the corresponding midday values are shown in the left panels of Figure 11. We consider a time interval from 9 UT to 15 UT when approximation of a horizontally uniform ionosphere within the medium where the signal propagates. A lack of data between 13 UT and 14 UT is due to a regular pause in the VLF/LF signals monitoring by the AWESOME receiver located in Belgrade.

To obtain the daytime evolution of $\beta$ and $H^{\prime }$, we first calculate their midday values. According to the database given at http://sidc.oma.be/silso/datafiles, the mean value of daily sunspot number for 20 days before and for the considered day is $\sigma$ = 107.1. Introducing these values in Equations (16) and (17) gives the midday Wait’s parameters for the analyzed day: ${\beta }_0^{\mathrm{midday}}=0.42$ km${}^{-1}$ and ${H_0^{\prime }}^{\mathrm{midday}}=72.5$ km. The recorded midday amplitude $A_{\mathrm{mod}}^{\mathrm{midday}}=30.35$ dB and phase $P_{\mathrm{mod}}^{\mathrm{midday}}=1.{11}^{°}$ are estimated from time evolutions of the corresponding signal characteristics. Finally, the time evolution of Wait’s parameters are calculated by the procedure as described in Section 2.2.2 and shown in the right panels of Figure 11. In the considered time period (excluding a short-term peak), these parameters have values within approximative domains 0.36 km${}^{-1}$–0.45 km${}^{-1}$ and 71.2 km–74.2 km, respectively. Comparisons of the data obtained by the QIonDR model with those calculated by the LWPC default and IRI (see Reference [52] and references therein; Wait’s parameters are calculated from electron density altitude distribution and expression for the electron density given in Reference [34]) models and with data presented in previous studies [27,33,35,53] show the best comparison of the QIonDR modeled amplitude and phase variations with the recorded ones. The QIonDR model fits better than the LWPC default model with data shown in References [27,33,35,53] for both Wait’s parameters. The IRI model agrees better with the QIonDR ones for $H_0^{\prime }$, as well as in some periods for ${\beta }_0$.

The daytime variation in the D-region electron density during the considered day, obtained from the calculated Wait’s parameters and Equation (15), is shown in Figure 12. The time variation of electron density is more noticeable at higher altitudes while the vertical changes are most pronounced in the midday period. Similarly to the comparison of Wait’s parameters, the QIonDR model fits better than the LWPC default model with data shown in References [27,33,35,53] for the electron density at 70 km and 80 km. The IRI model agrees better with the QIonDR ones for the electron densities at 70 km.

A similar analysis is provided also for the D-region disturbed by a solar X-ray flare on 17 September 2015 (signal characteristics for this event are shown in Figure 2). Comparisons of the amplitude and phase changes, as well as time evolutions of Wait’s parameters and the electron density for different values of initial Wait’s parameters, are shown in Figure 13. In these calculations, we applied the LWPC model for the initial Wait’s parameters obtained by the QIonDR, LWPC default, and IRI models, and based on the studies presented in References [27,35,53]. In all these cases, the modeled amplitude and phase variations are in very good agreement with the recorded ones. For better visibility, we show only the obtained data for the QIonDR and LWPC default models. As one can see in Figure 13a, they are practically completely fitted with the recorded data except for the end of the observed period when minor deviations are noticeable in the case of LWPC default program for the amplitude changes. Agreement of $\beta$ is better for QIonDR than for the LWPC default model with data obtained by IRI model and data from References [27,35], as well as for data from Reference [53], in some periods. In the cases of $H^{\prime }$ and electron density time evolutions, the QIonDR better fits with data obtained for initial parameters calculated by the IRI model, used in Reference [27], and, in some periods, for initial parameters given in Reference [35]. In addition, comparison of all parameters is in better agreement for the QIonDR than LWPC default model with data presented in References [26,29] for the maximum X-radiation flux of flares of the same or very similar class as the considered one.

5. Conclusions

In this paper, we present a procedure for calculations of the D-region plasma parameters during quiet conditions. The proposed methodology is applied to areas monitored by the VLF/LF radio signals emitted and recorded by relatively closely located transmitters and receivers like, for example, in Europe. It is based on two different VLF/LF signals acquired by one receiver. We applied the proposed methodology to the DHO and ICV signals emitted in Germany and Italy, respectively, and recorded in Serbia. The obtained results of this study are:

• A new procedure for estimation of Wait’s parameters and electron density. It is divided in two parts: (1) determination of dependencies of these parameters on the smoothed daily sunspot number and season at midday, and (2) determination of time evolution of these parameters during daytime;
• Estimation of Wait’s parameters and electron density over the part of Europe included within the location of the transmitted signals (Sardinia, Italy, for the ICV signal) and (Lower Saxony, Germany for the DHO signal) and the receiver in Belgrade, Serbia. The obtained results show variations in which inclusion in different analyses of more events or time periods will allow more realistic comparisons and statistic studies;
• Analytical expressions for dependencies of Wait’s parameters on the smoothed daily sunspot number and seasonal parameter valid over the studied area.

The determination of the “sharpness” $\beta$ and signal reflection height $H^{\prime }$ during quiet conditions are needed for calculations of the electron density and other plasma parameters in the D-region during both the quiet and disturbed conditions. As a consequence, a more realistic modeling of the D-region can be attained based on results obtained by the proposed methodology. This could benefit to statistical analyses of the D-region related to different unperturbed conditions subject to daily and seasonal variations, as well as variations during a solar cycle. Furthermore, the most accurate modeling of the D-region based on the results obtained by the proposed methodology could also improve the mitigation of ionospheric propagation artefacts in telecommunication and microwave Earth Observation applications.

Due to approximation of the horizontally uniform ionosphere and neglect of influence of geomagnetic field variations on the VLF/LF signal propagation, application of the presented model is limited to:

• Time periods during quiet conditions or during disturbances that do not affect the assumed horizontal uniformity of the observed D-region (for example, the midday periods during the influence of solar X-ray flares),
• VLF/LF signals in which propagation paths between transmitters and receivers are relatively short, and
• Mid- and low-latitude areas where the spatial variations of the magnetic field are not significant in the given conditions.

In other words, the presented model cannot be used when losses, gyrotropy and anisotropy in the region of 70–90 km can significantly affect the propagation of VLF/LF signals in the waveguide Earth-Ionosphre, in particular in situations of large geophysical disturbances of the Lithosphere-Atmosphere-Ionosphere-Magnetosphere system caused by large magnetic storms, hurricanes, etc.

The proposed methodology can be applied during the daytime period when the solar influence on the ionosphere is the largest. During this period the electron density can significantly rise due to influence of intensive sudden solar phenomena like a solar X-ray flare, which can further importantly affect propagation of the mentioned electromagnetic waves.

It is worth noting that the proposed methodology can be applied only to relatively small areas like the one studied in this paper. For this reason, it is more relevant for Europe characterized by a high density network of VLF/LF transmitters and receivers. Improvements of the receiver and/or transmitter networks in future will make the application of the proposed methodology more interesting in providing a real to near-real-time mapping of the D-region electron density above more regions around the world.