Refining Altimeter-Derived Gravity Anomaly Model from Shipborne Gravity by Multi-Layer Perceptron Neural Network: A Case in the South China Sea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Data
2.1.1. Reference Gravity Model and Topography Model
2.1.2. Shipborne Gravity
2.1.3. Altimeter-Derived Gravity Anomaly Model
2.2. Methodology
2.2.1. Structure of MLP
2.2.2. Refined Area Classification
2.2.3. Training and Predicting
3. Results
3.1. Refining the Gravity Model by Classification
3.2. Refining the Gravity Model as a Whole
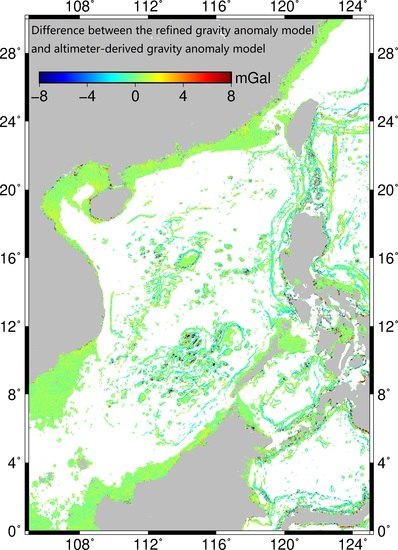
3.3. Analysis of the Refined Gravity Anomaly Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- King-Hele, D. The shape of the Earth. Science 1976, 192, 1293–1300. [Google Scholar] [CrossRef] [PubMed]
- Rathnayake, S.; Tenzer, R. Interpretation of the lithospheric structure beneath the Indian Ocean from gravity gradient data. J. Asian Earth Sci. 2019, 183, 103934. [Google Scholar] [CrossRef]
- Tenzer, R.; Gladkikh, V.; Novak, P.; Vajda, P. Spatial and spectral analysis of refined gravity data for modelling the crust-mantle interface and mantle-lithosphere structure. Surv. Geophys. 2012, 33, 817–839. [Google Scholar] [CrossRef]
- Hotta, H.; Kubota, R.; Ishikawa, H.; Oshida, A.; Okada, C.; Matsuda, T.; Asakawa, E. The goal of the integrated ocean resources survey system (“INORSS”). In Next-generation Technology for Ocean Resources Exploration of “SIP”; OCEANS—MTS/IEEE Kobe Techno-Oceans Conference: Kobe, Japan; New York, NY, USA, 2018. [Google Scholar]
- Bobojc, A. Application of gravity gradients in the process of GOCE orbit determination. Acta Geophys. 2016, 64, 521–540. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Chen, P.; Macabiau, C.; Han, C. Low-Earth orbit determination from gravity gradient measurements. Acta Astronaut. 2016, 123, 350–362. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.B.; Knudsen, P. The DTU17 global marine gravity field: First validation results. In Fiducial Reference Measurements for Altimetry, International Association of Geodesy Symposia; Mertikas, S., Pail, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 150. [Google Scholar]
- Sandwell, D.T.; Harper, H.; Tozer, B.; Smith, W.H.F. Gravity field recovery from geodetic altimeter missions. Adv. Space Res. 2019. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Muller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.; Hsu, H.Y. Shallow-water gravity anomalies from satellite altimetry: Case studies in the east China sea and Taiwan strait. J. Chin. Inst. Eng. 2008, 31, 841–851. [Google Scholar] [CrossRef]
- Zhang, S.; Sandwell, D.T.; Jin, T.; Li, D. Inversion of marine gravity anomalies over southeastern China seas from multi-satellite altimeter vertical deflections. J. Appl. Geophys. 2017, 137, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Gille, S.T.; Orcutt, J.; Smith, W.H.F. Bathymetry from space is now possible. EOS Trans. Am. Geophys. Un. 2003, 84, 37–44. [Google Scholar] [CrossRef]
- Kim, J.W.; von Frese, R.R.B.; Lee, B.Y.; Roman, D.R.; Doh, S.-J. Altimetry-derived gravity predictions of bathymetry by the gravity-geologic method. Pure Appl. Geophys. 2010, 168, 815–826. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Li, X.; Yang, J.; Wan, X. Seafloor Topography estimation from gravity anomaly and vertical gravity gradient using nonlinear iterative least square method. Remote Sens. 2021, 13, 64. [Google Scholar] [CrossRef]
- Zaki, A.; Mansi, A.H.; Selim, M.; Rabah, M.; El-Fiky, G. Comparison of satellite altimetric gravity and global geopotential models with shipborne gravity in the Red Sea. Mar. Geodesy 2018, 41, 258–269. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, J.; Hwang, C.; Gao, J.; Yuan, J.; Liu, X. How HY-2A/GM altimeter performs in marine gravity derivation: Assessment in the South China Sea. Geophys. J. Int. 2019, 219, 1056–1064. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Guo, J.; Zhu, C.; Yuan, J.; Gao, J.; Gao, Y.; Ji, B. Performance of Jason-2/GM altimeter in deriving marine gravity with the waveform derivative retracking method: A case study in the South China Sea. Arab. J. Geosci. 2020, 13, 939. [Google Scholar] [CrossRef]
- Huang, M.; Wang, R.; Zhai, G.; Ouyang, Y. Integrated data processing for multi-satellite missions and recovery of marine gravity field. Geomat. Informat. Sci. Wuhan Univ. 2007, 32, 988–993. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.H. Regional Gravity Field Modeling from Heterogeneous Data Sets by Using Poisson Wavelets Radial Basis Functions. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Guo, J.; Liu, X.; Chen, Y.; Wang, J.; Li, C. Local normal height connection across sea with ship-borne gravimetry and GNSS techniques. Mar. Geophys. Res. 2014, 35, 141–148. [Google Scholar] [CrossRef]
- Hwang, C.; Parsons, B. Gravity anomalies derived from Seasat, Geosat, ERS-1 and TOPEX/POSEIDON altimetry and ship gravity: A case study over the Reykjanes Ridge. Geophys. J. Int. 1995, 122, 551–568. [Google Scholar] [CrossRef]
- Paolo, F.S.; Molina, E.C. Integrated marine gravity field in the Brazilian coast from altimeter-derived sea surface gradient and shipborne gravity. J. Geodynam. 2010, 50, 347–354. [Google Scholar] [CrossRef]
- Wu, Y.H.; Luo, Z.C.; Zhou, B.Y. Regional gravity modeling based on heterogeneous data sets by using Poisson wavelets radial basis functions. Chin. J. Geophys. 2016, 59, 852–864. [Google Scholar]
- Samuel, A.L. Some studies in machine learning using the game of checkers. IBM J. 1959, 3, 211–229. [Google Scholar] [CrossRef]
- Bengio, Y.; Lecun, Y. Scaling learning algorithms towards AI. In Large-Scale Kernel Machines; Chapelle, O., Decoste, D., Eds.; MIT Press: Cambridge, UK, 2007; pp. 321–358. [Google Scholar]
- Bengio, Y.; Delalleau, O. On the expressive power of deep architectures. In Proceeding of the 14th International Conference on Discovery Science, Espoo, Finland, 5–7 October 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 18–36. [Google Scholar]
- Widiasari, I.R.; Nugroho, L.E.; Widyawan, W. Deep learning multilayer perceptron (MLP) for flood prediction model using wireless sensor network based hydrology time series data mining. In Proceedings of the International Conference on Innovative and Creative Information Technology, Salatiga, Indonesia, 2–4 November 2017; IEEE: New York, NY, USA, 2017. [Google Scholar]
- Vafaeipour, M.; Rahbari, O.; Rosen, M.A.; Fazelpour, F.; Ansarirad, P. Application of sliding window technique for prediction of wind velocity time series. Int. J. Energy Environ. Eng. 2014, 5, 105. [Google Scholar] [CrossRef] [Green Version]
- Voyant, C.; Nivet, M.L.; Paoli, C.; Muselli, M.; Notton, G. Meteorological time series forecasting based on MLP modelling using heterogeneous transfer functions. J. Phys. Conf. Ser. 2015, 574, 012064. [Google Scholar] [CrossRef] [Green Version]
- Voyant, C.; Paoli, C.; Muselli, M.; Nivet, M.L. Multi-horizon solar radiation forecasting for Mediterranean locations using time series models. Renew. Sustain. Energy Rev. 2013, 28, 44–52. [Google Scholar] [CrossRef] [Green Version]
- Guan, D.L.; Ke, X.P.; Wang, Y. Basement structures of East and South China Seas and adjacent regions from gravity inversion. J. Asian Earth Sci. 2016, 117, 242–255. [Google Scholar] [CrossRef]
- Hwang, C.; Chang, E.T.Y. Seafloor secrets revealed. Science 2014, 346, 32–33. [Google Scholar] [CrossRef] [PubMed]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, B04406. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.T.; Garcia, E.; Soofi, K.; Wessel, P.; Chandler, M.; Smith, W.H.F. Toward 1-mGal accuracy in global marine gravity from CryoSat-2, Envisat, and Jason-1. Lead. Edge 2013, 32, 892–899. [Google Scholar] [CrossRef] [Green Version]
- Amante, C.; Eakins, B.W. ETOPO1 1 arc-minute global relief model: Procedures, data sources and analysis. In NOAA Technical Memorandum NESDIS NGDC-24; National Geophysical Data Center, NOAA: Miami, FL, USA, 2009. [Google Scholar]
- Wessel, P.; Watts, A.B. On the accuracy of marine gravity measurements. J. Geophys. Res. Solid Earth 1988, 93, 393–413. [Google Scholar] [CrossRef]
- Zhu, C.; Guo, J.; Gao, J.; Liu, X.; Hwang, C.; Yu, S.; Yuan, J.; Ji, B.; Guan, B. Marine gravity determined from multi-satellite GM/ERM altimeter data over the South China Sea: SCSGA V1.0. J. Geodesy 2020, 94, 50. [Google Scholar] [CrossRef]
- Hwang, C. Inverse Vening Meinesz formula and deflection-geoid formula: Applications to the predictions of gravity and geoid over the South China Sea. J. Geodesy 1998, 72, 304–312. [Google Scholar] [CrossRef]
- Shiblee, M.; Kalra, P.K.; Chandra, B. Time series prediction with multilayer perceptron (MLP): A new generalized error based approach. In International Conference on Neural Information Processing, Auckland, New Zealand, 2008; Koppen, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 37–44. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cagli, E.; Dumas, C.; Prouff, E. Convolutional Neural Networks with Data Augmentation Against Jitter-Based Countermeasures. In International Conference on Cryptographic Hardware and Embedded Systems, Taiwan, China, 2017; Fischer, W., Homma, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 45–68. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning Publication Co.: New York, NY, USA, 2018. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proccedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Pujol, M.-I.; Schaeffer, P.; Faugère, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the improvement of recent mean sea surface models: A new approach for identifying and quantifying their errors. J. Geophys. Res. Ocean 2018, 123, 5889–5911. [Google Scholar] [CrossRef]
- Yuan, J.; Guo, J.; Niu, Y.; Zhu, C.; Li, Z. Mean sea surface model over the sea of Japan determined from multi-satellite altimeter data and tide gauge records. Remote Sens. 2020, 12, 4168. [Google Scholar] [CrossRef]
- CNES. Along-Track Level-2+ (L2P) SLA Product Handbook; SALP-MU-P-EA-23150-CLS, Issue1.0; CNES: Paris, France, 2017.








| Submarine Topography Slope (m/arcmin a) | Shipborne Data before 1990 (mGal) | Shipborne Data Since 1990 (mGal) |
|---|---|---|
| All | 4.41 | 3.93 |
| N > 50 or E > 50 b | 4.55 | 4.16 |
| N > 100 or E > 100 | 4.89 | 4.17 |
| N > 150 or E > 150 | 5.10 | 4.38 |
| Satellite | Period | Inter-Track Distance at Equator (km) | Sampling Interval along Track (km) |
|---|---|---|---|
| ERS-1 | 94.04–95.03 | 7 | 6.6 |
| Jason-1 | 12.05–13.06 | 7 | 5.8 |
| Jason-2 | 17.07–19.02 | 7 | 5.8 |
| HY-2A | 16.03–18.07 | 15 | 6.5 |
| SARAL–AltiKa | 16.07–18.10 | 5 | 6.9 |
| CryoSat-2 | 11.01–18.07 | 2.5 | 6.4 |
| Bathymetry (m) | 0–10 | 10–20 | 20–30 | 30–40 | 40–50 | 50–60 | 60–70 | 70–100 |
|---|---|---|---|---|---|---|---|---|
| RMS (mGal) | 10.48 | 7.80 | 6.54 | 7.63 | 6.41 | 5.59 | 4.48 | 3.89 |
| STD (mGal) | 9.80 | 7.74 | 6.31 | 7.59 | 6.36 | 5.53 | 4.48 | 3.84 |
| Slopes (m/arcmin) | All | E > 50 or N > 50 | E > 100 or N > 100 | E > 150 or N > 150 |
|---|---|---|---|---|
| RMS (mGal) | 5.36 | 5.88 | 6.28 | 6.37 |
| STD (mGal) | 5.35 | 5.85 | 6.22 | 6.30 |
| Category | Bathymetry 50 m | Submarine Topography Slope | Number of Samples | Number of Predicted Grid Points | |
|---|---|---|---|---|---|
| Prime Vertical 100 m/arcmin | Meridian 100 m/arcmin | ||||
| Case1 | < | ≤ | ≤ | 795 | 245,314 |
| < | > | ≤ | |||
| < | ≤ | > | |||
| < | > | > | |||
| Case2 | ≥ | > | > | 3431 | 52,692 |
| Case3 | ≥ | > | ≤ | 7612 | 74,093 |
| Case4 | ≥ | ≤ | > | 5260 | 76,225 |
| Layer | Variable | Vector Size | |
|---|---|---|---|
| Input layer | Input | (256,146) | |
| Output | (256,146) | ||
| Hidden layer | 1 | Input | (256,146) |
| Output | (256,512) | ||
| 2 | Input | (256,512) | |
| Output | (256,256) | ||
| Output layer | Input | (256,256) | |
| Output | (256,1) | ||
| Refined Area | Case1 | Case2 | Case3 | Case4 | ||
|---|---|---|---|---|---|---|
| Number | 99,048 | 11,343 | 24,222 | 30,815 | 32,668 | |
| V1.0- NCEI | MEAN | −0.59 | −0.06 | −0.77 | −0.80 | −0.44 |
| STD | 5.78 | 5.80 | 6.16 | 5.70 | 5.54 | |
| RMS | 5.81 | 5.80 | 6.21 | 5.75 | 5.55 | |
| V1.1- NCEI | MEAN | −0.36 | 0.04 | −0.58 | −0.30 | −0.40 |
| STD | 5.66 | 5.65 | 6.06 | 5.54 | 5.45 | |
| RMS | 5.67 | 5.65 | 6.09 | 5.55 | 5.46 | |
| Refined Area | Case1 | Case2 | Case3 | Case4 | ||
|---|---|---|---|---|---|---|
| Number | 99,048 | 11,343 | 24,222 | 30,815 | 32,668 | |
| V1.2- NCEI | MEAN | −0.40 | −0.38 | −0.55 | −0.40 | −0.30 |
| STD | 5.65 | 5.68 | 6.04 | 5.58 | 5.40 | |
| RMS | 5.67 | 5.69 | 6.06 | 5.57 | 5.41 | |
| Refined Area | Case1 | Case2 | Case3 | Case4 | |||
|---|---|---|---|---|---|---|---|
| Region A | Number | 7626 | 189 | 1682 | 2421 | 3334 | |
| V1.0- NCEI | MEAN | 0.14 | −0.85 | 0.78 | −0.44 | 0.28 | |
| STD | 5.91 | 5.75 | 6.36 | 6.15 | 5.45 | ||
| RMS | 5.91 | 5.81 | 6.41 | 6.16 | 5.46 | ||
| V1.2- NCEI | MEAN | 0.18 | −1.50 | 0.70 | −0.22 | 0.30 | |
| STD | 5.65 | 5.49 | 6.03 | 5.95 | 5.18 | ||
| RMS | 5.65 | 5.69 | 6.07 | 5.95 | 5.19 | ||
| Region B | Number | 91,422 | 11,154 | 22,540 | 28,394 | 29,334 | |
| V1.0- NCEI | MEAN | −0.65 | −0.05 | −0.88 | −0.83 | −0.52 | |
| STD | 5.76 | 5.80 | 6.13 | 5.65 | 5.54 | ||
| RMS | 5.80 | 5.80 | 6.19 | 5.71 | 5.56 | ||
| V1.2- NCEI | MEAN | −0.45 | −0.36 | −0.65 | −0.42 | −0.36 | |
| STD | 5.65 | 5.68 | 6.03 | 5.55 | 5.43 | ||
| RMS | 5.67 | 5.69 | 6.06 | 5.57 | 5.44 | ||
| Gravity Model | Refined Area | Case1 | Case2 | Case3 | Case4 |
|---|---|---|---|---|---|
| SCSGA V1.0 | 5.81 | 5.80 | 6.21 | 5.75 | 5.55 |
| SCSGA V1.2 | 5.67 | 5.69 | 6.06 | 5.57 | 5.41 |
| M1 | 5.75 | 5.77 | 6.13 | 5.66 | 5.53 |
| M2 | 5.71 | 5.73 | 6.08 | 5.64 | 5.49 |
| M3 | 5.70 | 5.83 | 6.05 | 5.62 | 5.46 |
| Depth (m) | MAX | MIN | MEAN | STD | RMS |
| 0–10 | 17.55 | −23.55 | 0.36 | 1.85 | 1.89 |
| 10–20 | 15.74 | −15.43 | 0.40 | 1.64 | 1.69 |
| 20–30 | 19.25 | −18.53 | 0.46 | 1.43 | 1.50 |
| 30–40 | 12.67 | −14.42 | 0.40 | 1.25 | 1.31 |
| 40–50 | 13.80 | −16.20 | 0.35 | 1.10 | 1.15 |
| Slopes (m/arcmin) | MAX | MIN | MEAN | STD | RMS |
| N > 100 or E > 100 | 20.05 | −23.78 | −0.18 | 2.01 | 2.02 |
| N > 150 or E > 150 | 19.94 | −23.78 | −0.14 | 2.23 | 2.23 |
| N > 200 or E > 200 | 17.52 | −23.78 | −0.11 | 2.44 | 2.44 |
| N > 300 or E > 300 | 17.52 | −21.98 | −0.05 | 2.86 | 2.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Guo, J.; Yuan, J.; Jin, X.; Gao, J.; Li, C. Refining Altimeter-Derived Gravity Anomaly Model from Shipborne Gravity by Multi-Layer Perceptron Neural Network: A Case in the South China Sea. Remote Sens. 2021, 13, 607. https://doi.org/10.3390/rs13040607
Zhu C, Guo J, Yuan J, Jin X, Gao J, Li C. Refining Altimeter-Derived Gravity Anomaly Model from Shipborne Gravity by Multi-Layer Perceptron Neural Network: A Case in the South China Sea. Remote Sensing. 2021; 13(4):607. https://doi.org/10.3390/rs13040607
Chicago/Turabian StyleZhu, Chengcheng, Jinyun Guo, Jiajia Yuan, Xin Jin, Jinyao Gao, and Chengming Li. 2021. "Refining Altimeter-Derived Gravity Anomaly Model from Shipborne Gravity by Multi-Layer Perceptron Neural Network: A Case in the South China Sea" Remote Sensing 13, no. 4: 607. https://doi.org/10.3390/rs13040607
APA StyleZhu, C., Guo, J., Yuan, J., Jin, X., Gao, J., & Li, C. (2021). Refining Altimeter-Derived Gravity Anomaly Model from Shipborne Gravity by Multi-Layer Perceptron Neural Network: A Case in the South China Sea. Remote Sensing, 13(4), 607. https://doi.org/10.3390/rs13040607