1. Introduction
In recent years, with the increasing emphasis on marine resources, long-distance detecting, tracking, and early warning of maritime targets have become the top priority of the current maritime rights protection work. High frequency surface wave radar (HFSWR), which achieves over-the-horizon detection of sea-surface targets and sea-skimming targets at low altitude, is an efficient way for ocean surveillance. Compared with shore-based HFSWR, shipborne HFSWR has better survivability, flexibility, and maneuverability. However, the movement of the platform causes the spread of the first-order sea clutter, which will obscure targets with low radial velocity like ships. How to detect the targets submerged in the clutter has become the focus of research on signal processing in shipborne HFSWR.
The premise of clutter suppression is that the clutter and the target are distinguishable in a certain dimension. The characteristics of the clutter and target should be studied before designing a clutter suppression approach. The properties of the spread spectrum of first-order sea clutter has been analyzed and a technique for ship target detection by using the sum-and-difference beamformer was proposed [
1]. The space–time distribution of the first-order sea clutter for shipborne HFSWR has been demonstrated and the linear relationship between the Doppler frequency and the azimuth cosine of the first-order sea clutter was pointed out [
2]. This means that it is theoretically possible to calculate the azimuth angle of the clutter patch for the determined Doppler frequency unit. Based on this, two spatial projection algorithms, orthogonal weighting (OW) [
3] and oblique projection (OP) [
4], have been proposed. By projecting the target and clutter to a subspace orthogonal to the clutter subspace, the clutter can be eliminated. Compared with the OW algorithm, the OP algorithm makes the projection space parallel to the target subspace to maintain the gain of the target during the projection process. Nevertheless, the calculated clutter direction is only a theoretical value, and errors often occur in the actual situation, resulting in performance degradation. A linear beamformer has been proposed for clutter cancellation with the help of a flat top beam, difference beam, and an auxiliary estimator beam in [
5]. These above approaches suppress clutter by forming nulls in the spatial domain. The difference in azimuth between the target and the clutter is used to separate them.
Considering the difference in the space–time distribution between the first-order sea clutter and the target, suppressing the clutter in the spatial and temporal dimension simultaneously will have better performance. Space–time adaptive processing (STAP) has been proven to be an effective clutter suppression algorithm for this kind of clutter. Some direct-from STAP methods like joint domain localized (JDL), improved orthogonal weighting (IOW), and improved oblique projection (IOP) have been proposed for clutter suppression in shipborne HFSWR [
6,
7,
8,
9,
10,
11,
12]. Except for the direct-form processor structure, like the methods above-mentioned, the STAP algorithm can be implemented in the generalized sidelobe canceler (GSC) structure [
13]. The GSC is a beamforming structure that can be used as an implementation of linearly constrained adaptive array processors [
14] and is a spatial filtering technology. Some main-lobe cancellation methods have been proposed based on this structure for clutter suppression in HFSWR [
15,
16,
17,
18,
19,
20,
21,
22,
23]. A single notch space filter has been designed for target blocking, meanwhile the virtual sliding subarrays were used to obtain secondary beams, which would increase the degree of freedom (DOF) [
18,
20,
21,
23]. A rotating spatial beam was proposed [
19,
22] that works as a blocking matrix and obtains secondary beams for small-aperture arrays. The auxiliary channel STAP is one of the GSC-structure beam-space post-Doppler STAP methods. Only parts of the angle-Doppler channels are selected as auxiliary channels. Unlike JDL processing, which assumes that the angular-Doppler channels surrounding the main channel are most important, the conventional auxiliary channel STAP selects auxiliary channels along the clutter ridge. There are some papers about the application of this clutter suppression method in airborne radar [
24,
25,
26,
27,
28,
29,
30,
31,
32]; however, there is no literature on the application of this method in shipborne HFSWR.
In this paper, the auxiliary channel STAP method was extended to shipborne HFSWR. Improvements were also been made based on the conventional auxiliary channel STAP method to optimize the performance of clutter suppression, which mainly consists of two aspects: one is the prior knowledge based auxiliary channels selecting approach and the other is the training samples selecting approach. The auxiliary channels are selected according to the space–time distribution of the first-order sea clutter to obtain precise clutter information. The training samples were selected according to the Riemannian distance to deal with the heterogeneous clutter in shipborne HFSWR. The rest of this paper is structured as follows. The signal model of shipborne HFSWR is formulated in
Section 2. The proposed auxiliary channel STAP algorithm is demonstrated in
Section 3. The proposed method was evaluated with measured data in
Section 4;
Section 5 gives the discussion; and the conclusions are presented in
Section 6.
Notation: Scalar quantities are denoted with lightface letters. Vectors and matrices are denoted by boldface lowercase and uppercase letters, respectively. represents the complex field. The conjugation of a complex number is denoted by . The transpose, conjugate transpose, and inverse of a matrix are denoted by the superscripts , , and respectively. The Kronecker product of two matrixes is represented by . The expectation operator is denoted by . The rounding operator, which indicates rounding to the nearest integer, is denoted by . The absolute value of a scalar or the determinant of a square matrix is denoted by . The 2 norm and Frobenius norm of a matrix are denoted by and , respectively. The trace of a square matrix is represented by .
2. Shipborne High Frequency Surface Wave Radar (HFSWR) Signal Model
Assume that the receiving subsystem of the radar consists of
N receiving antennas that form a uniform linear array (ULA). The transmitting subsystem transmits a burst of
M pulses during the coherent processing interval (CPI). For each channel and each pulse, the received array data are sampled and preprocessed to obtain range samples. The
kth range cell takes the form
where
represents the data collected from the
mth pulse and
denotes transposition.
The received data snapshot
is the sum of three parts, target, clutter, and noise, denoted
,
, and
, respectively. It is mathematically written as
The target snapshot, denoted
, can be expressed as the product of complex amplitude
and space–time steering vector
, and can be written as
where the space–time steering vector of the target, denoted
, is the Kronecker product of the spatial steering vector
and the temporal steering vector
, and is written as
where the mathematical symbol
is the Kronecker product. The spatial steering vector and the temporal steering vector take the form,
where
and
are the normalized spatial and Doppler frequency, respectively. The symbols
and
d represent the wavelength and the interelement spacing of the ULA, respectively. The azimuth of the target and the Doppler frequency of the target are denoted by
and
, respectively. The pulse repetition interval (PRI) is denoted by
.
Thus, the covariance matrix of the target signal can be derived as
where
indicates the expectation operator.
The clutter snapshot
in HFSWR is mainly composed of the first-order and second-order sea clutter, and the energy of the second-order sea clutter is usually 20–45 dB smaller than that of the first-order [
33]. Therefore, the second-order sea clutter can be ignored. The clutter in a certain range cell can be regarded as the superposition of a large number of uncorrelated clutter patches [
34,
35], which has the expression as follows,
where
denotes the
qth clutter patch in the
kth range bin; the complex amplitude of the receding (caused by ocean waves going away from the radar) and approaching (caused by ocean waves coming toward the radar) first-order ocean clutter are denoted by
and
, respectively; their corresponding Doppler frequency are denoted by
and
, respectively; and the azimuth of the
qth clutter patch in the
kth range bin is denoted by
. Under ideal conditions, there is a linear relationship between the Doppler frequency
and the azimuth cosine
of the clutter patch, as described in [
2],
where
denotes the platform velocity. The symbol
is the first-order Bragg frequency, and is calculated using the system carrier frequency
in MHz.
The the clutter covariance matrix (CCM) was analyzed in [
34,
35] and has the following expression
For a fully-developed sea where the energy supplied by the wind is equal to the energy lost in breaking waves, its surface is a random surface. According to [
34,
36,
37], the random amplitudes of the harmonic components of electromagnetic waves scattered off a random surface are uncorrelated. Thus, the first-order sea clutter from different ocean patches can be assumed as uncorrelated. The complex amplitudes of the preceding and approaching Bragg components from the same clutter patch are also assumed to be uncorrelated. The CCM is simplified to
The rank of the CCM for shipborne HFSWR is derived in a precise expression in [
35], as
where the factors
and
are calculated as
and
; the PRI
in
is calculated as
; and the operator
indicates rounding to the nearest integer.
The noise snapshot
can be assumed as a complex Gaussian distribution with zero-mean and the power
. The noise covariance matrix is
3. Knowledge-Based Auxiliary Channel Space–Time Adaptive Processing (STAP)
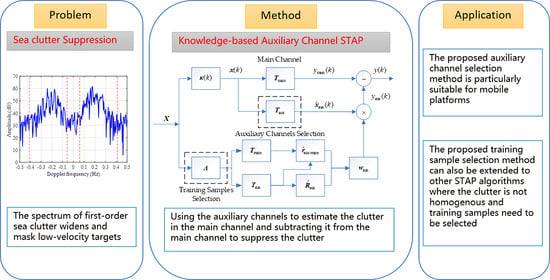
Auxiliary channel STAP is one of the GSC-structure STAP methods. The core of auxiliary STAP is to estimate the clutter in the main channel using the clutter in auxiliary channels. In this section, a knowledge-based auxiliary channel STAP algorithm is presented for spreading sea clutter suppression in shipborne HFSWR.
3.1. Auxiliary Channel Space–Time Adaptive Processing (STAP)
For the kth range cell data , assume that the azimuth of the target and the Doppler frequency of the target are denoted by and , respectively.
The main channel, denoted by
, is calculated as
where
is the transformation matrix, which has the same representation with the space–time steering vector of the target,
Assume that
D auxiliary channels are selected, the auxiliary channels, denoted by
, are calculated as,
where
is the transformation matrix for auxiliary channels.
After transforming into the angle-Doppler domain, the main channel data
is the sum of the target, the first-order sea clutter, and noise. As the following equation denotes,
If the clutter in the auxiliary channels is related to that in the main channel, it can be estimated from the auxiliary channels. This estimation, denoted by
, is named as the output of auxiliary channels, and can be denoted by the following equation,
Subtracting the estimated clutter plus noise
from the main channel and the output of the auxiliary channel STAP processor,
is
where
is the residual term of the clutter and noise.
The weights vector
can be determined by the solution of the following least squares problem
The solution is given by
where
is the self-correlation matrix of the auxiliary channel, and
is the cross-correlation vector between the auxiliary channels and the main channel.
It is worth noting that
and
are unknown in practice and the maximum likelihood estimate is commonly used
where
,
are the secondary data.
The framework of the auxiliary channel STAP algorithm is illustrated in
Figure 1.
As shown in
Figure 1, for the input range cell data
, after a transformation (Doppler processing and beam forming), the data are converted into the beam-Doppler space, and the auxiliary channels are selected in it. After that, the adaptive weight vector of the auxiliary channels is calculated according to the minimum mean square error (MMSE) criterion and the output of the auxiliary channels is calculated. Finally, the output of the auxiliary channels is subtracted from the main channel output to suppress the clutter.
The performance of the auxiliary channel STAP method is mainly affected by how the auxiliary channels are selected and the estimation accuracy of the weights vector
. The selection of auxiliary channels is determined as the transformation matrix
and the estimation accuracy of
is determined by the training samples used when calculating the self-correlation matrix
and cross-correlation vector
. Therefore, for these two directions, a knowledge-based auxiliary channel selection approach and a training sample selection approach are proposed in
Section 3.2 and
Section 3.3 to improve the performance of the auxiliary channel STAP method.
3.2. Knowledge-Based Auxiliary Channels Selection
For shipborne HFSWR, the distribution of the first-order sea clutter is two straight lines on the angle-Doppler plane. Setting as abscissa and as the vertical coordinate, Equation (9) is rewritten as . After transformation, the formula is obtained. The wavelength , the platform velocity , and the Bragg frequency are constant. Hence, two single straight lines (clutter ridge) are expected in the angle-Doppler domain. One is the negative part , and the other is the positive part . These two straight lines are determined by system parameters and can be seen as prior knowledge.
A data acquisition experiment was conducted in the Yellow Sea of China in September 1998. The data acquisition system consists of a transmitting subsystem, a receiving subsystem, and a data acquisition subsystem. The transmitting subsystem is made of an omnidirectional antenna, and the signal used is frequency modulated interrupted continuous wave (FMICW). The receiving subsystem includes seven antennas that form a uniform linear broadside array. The geometry of the receiving array is illustrated in
Figure 2.
The whole system was mounted on a barge, which was tugged by a tugboat. As described in [
1,
3,
7,
12], the system parameters are shown in
Table 1.
Figure 3 illustrates the range-Doppler map and the angle-Doppler map of the measured data. The dashed line in
Figure 3a represents the spreading region of the first-order sea clutter. The dashed line in
Figure 3b denotes the clutter ridge.
For auxiliary channel STAP, auxiliary channels should contain clutter with the same characteristics as the main channel. Due to the wider beam width in the spatial domain, the main channel will contain some clutter components from the clutter ridge. Thus, we can utilize this prior knowledge and select auxiliary channels along the clutter ridge of the first-order sea clutter.
Figure 4 shows the sketch map of the main channel and auxiliary channels. If the targets fall in the spreading range of the first-order sea clutter, the clutter plus noise component
in the main channel can be approximated from the clutter ridge.
According to the prior knowledge, the auxiliary channels selecting matrix
were chosen as a set of the space–time steering vectors of the first-order sea clutter.
where
and
are the Doppler frequency and the azimuth of the clutter patches, respectively. They satisfy Equation (9).
The quantity of auxiliary channels, denoted by
D, is discussed as follows. The total number of auxiliary channels available is determined by how the clutter ridge is defined.
Figure 5 illustrates the theoretical clutter ridge and two different extracted clutter ridges from the measured data.
Taking the theoretical clutter ridge in
Figure 5a as an example, the quantity of auxiliary channels available when only one beam channel is selected for a determined Doppler frequency, can be calculated as
where
represents the Doppler resolution. In this situation, the number of auxiliary channels is equal to the number of Doppler channels. According to Equation (9), the spreading range of first-order sea clutter is
in the negative Doppler frequency and
in the positive Doppler frequency. The number of Doppler channels is
in the positive part or the negative part. Hence, the quantity of auxiliary channels is
. This usually numbers between tens and hundreds, which means that there are plenty of auxiliary channels for selecting.
It is worth noting that
also works as the blocking matrix and should satisfy
. Here, we chose one column of
to calculate the inner product
.
Figure 6 illustrates the value of
when
and
changes.
M is 1024 and
N equals 7. The
x-axis
represents the difference of the normalized temporal frequency between the target and clutter;
y-axis
is the difference of the normalized spatial frequency between the target and clutter. It can be seen from the result that as long as
is not zero,
is close to zero. Therefore, if the auxiliary channels and the main channel are not in the same Doppler bin, the transforming matrix used for the auxiliary channels can block the target signal.
Based on the analysis, the principle of auxiliary channel selection is to select auxiliary channels from the clutter ridge and the Doppler frequency of the auxiliary channels should be different from the main channel.
3.3. Training Sample Selection
When the auxiliary channels are determined, the performance of the auxiliary channel STAP is determined by the estimation accuracy of the auto-correlation matrix and the cross-correlation vector . Assuming that the noise is not related to the signal and clutter, and the blocking matrix can block the target signal well, the estimation accuracy is discussed below.
For the cross-correlation vector
, it can be decomposed as follows:
The first part may not be equal to a zero-vector due to limited training samples, especially when the target appears in multiple range bins or the target power is relatively strong. Under these circumstances, the target signal of the main channel will leak into the auxiliary channels and lead to target self-cancellation. This phenomenon can be reduced by setting guard range cells around the cell under test (CUT) and selecting training samples without targets.
For the auto-correlation matrix
, it can be decomposed as
Considering the decomposition results, the estimation accuracy is mainly affected by the training samples used. For shipborne HFSWR, the heterogeneity of clutter in range has been analyzed based on measured data in our previous work [
12]. The qualified independent and identically distributed (IID) training samples are limited. How to select the most homogeneous clutter sample in the finite training samples becomes important. The clutter in the training samples should be as similarly distributed as possible to the CUT. To measure the similarity, the Riemannian distance is introduced and a training samples selecting method is proposed here.
First, the explanation of the Riemannian distance is given. Different from the Euclidean distance used in [
22,
38], the Riemannian distance puts the covariance matrix on the Riemannian manifold, and the length of the shortest curve connecting two matrix
and
is defined as the Riemannian distance. The calculation of the Riemannian distance is given in [
39], and the expression is as follows,
where
is the trace of the matrix;
represents the matrix’s Frobenius norm and is calculated as
; and the eigenvalue of
is denoted by
.
Then, calculate the Riemannian distances between the clutter’s self-correlation matrix of CUT and other range cells using the following equations
After that, sort the distances
in ascending order and choose
L range cells with lower geometric distances. For the convenience of explaining the sample selection approach, a selecting matrix
which satisfies
, is defined. It has the following expression
Hence, the training sample selecting matrix
can be written as
where
is the same size as
and describes the arrangement of the elements of
into
along the sorted dimension and
.
The selected training samples
can be denoted as
As for the number of the training samples, it has a lower limit. The rank of the self-correlation matrix
should satisfy
where
represents the local covariance matrix of the clutter (after transforming into the angle-Doppler domain). By Equation (12), the local DOF of clutter can be approximated as
where
and
are the beams and Doppler bins in the local processing region (LPR), respectively. In this paper, there was only one beam and one Doppler bin in the LPR. Thus, the local DOF of clutter was approximated to
. As stated by the Reed–Mallett–Brennan (RMB) criterion [
40], the secondary data used to estimate the self-correlation matrix and cross-correlation vector should be twice the DOF of the clutter, which means that at least
IID secondary data are needed.
In conclusion, the procedural of the training sample selection approach can be summarized as follows:
Calculate the clutter covariance matrix using Equations (16) and (33);
Calculate the Riemannian distances between the CUT and other range cells using Equation (32);
Set as guard range cells to avoid target self-cancellation and sort in ascending order as Equation (36) denotes;
Select range cells, which has the lowest values of to formulate the selecting matrix using Equation (35), and the training samples are obtained as Equation (37).
6. Conclusions
In this paper, an auxiliary channel STAP algorithm was presented for suppressing the spreading first-order sea clutter in shipborne HFSWR. To obtain better clutter suppression results, this paper improved the STAP algorithm from two aspects. First, a method for selecting auxiliary channels was presented, which employs the knowledge of the space–time distribution of the first-order sea clutter; second, to deal with the heterogeneity of the clutter in range dimension and obtain an accurate estimation of the CCM, a training sample selection method was proposed based on the Riemannian distance between the CUT and other range cells. The range cells that were more similar to the CUT were selected. The performance of the proposed algorithm was evaluated with the measured data. Results showed that for the simulated targets, there was average of 26 dB SCNR improvement after conducting the proposed clutter suppression algorithm, and for the real target, the SCNR improvement reached 16 dB. Compared with FFT–DBF, IOW, IOP, and the conventional JDL algorithm, the proposed algorithm had a better performance when evaluating by the SCNR improvement for both the simulated and real targets, which indicates that the proposed algorithm is effective and superior.