Passive Remote Sensing of Ice Cloud Properties at Terahertz Wavelengths Based on Genetic Algorithm
Abstract
:1. Introduction
2. Basic Principles
2.1. Process of Ice Cloud Inversion at Terahertz
2.2. Selection of Channel Sets
3. Method for Ice Cloud Inversion
3.1. Forward Radiative Transfer Model
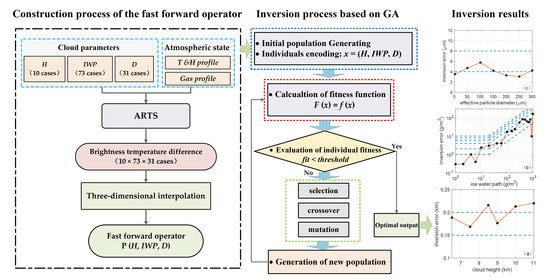
3.2. Construction of Fast Forward Operator
3.3. Inversion Method Based on the Genetic Algorithm
- Step 1: Initialization (Including Individual Encoding and Generation of Initial Population)
- Step 2: Fitness Scaling
- Step 3: Genetic Operations (Including Selection, Crossover and Mutation)
4. Application of the Method and Results
4.1. Verification of the Fast Forward Operator
4.2. Ice Cloud Inversion Error Analysis
5. Discussion and Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gultepe, I.; Rabin, R.; Ware, R.; Pavolonis, M. Light Snow Precipitation and Effects on Weather and Climate. Adv. Geophys. 2016, 57, 14. [Google Scholar] [CrossRef]
- Gultepe, I.; Heymsfield, A.J. Introduction Ice Fog, Ice Clouds, and Remote Sensing. Pure Appl. Geophys. 2016, 173, 2977–2982. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Hioki, S.; Saito, M.; Kuo, C.P.; Baum, B.A.; Liou, K.N. A Review of Ice Cloud Optical Property Models for Passive Satellite Remote Sensing. Atmosphere 2018, 9, 499. [Google Scholar] [CrossRef] [Green Version]
- Duncan, D.I.; Eriksson, P. An update on global atmospheric ice estimates from satellite observations and reanalyses. Atmos. Chem. Phys. 2018, 18, 11205–11219. [Google Scholar] [CrossRef] [Green Version]
- Carro-Calvo, L.; Hoose, C.; Stengel, M.; Salcedo-Sanz, S. Cloud glaciation temperature estimation from passive remote sensing data with evolutionary computing. J. Geophys. Res. Atmos. 2016, 121, 13591–13608. [Google Scholar] [CrossRef] [Green Version]
- Gultepe, I.; Feltz, W.F. Aviation Meteorology: Observations and Models. Introduction. Pure Appl. Geophys. 2019, 176, 1863–1867. [Google Scholar] [CrossRef] [Green Version]
- Wielicki, B.A.; Barkstrom, B.R.; Baum, B.A.; Charlock, T.P.; Green, R.N.; Kratz, D.P.; Lee, R.B.; Minnis, P.; Smith, G.L.; Wong, T.; et al. Clouds and the Earth’s Radiant Energy System (CERES): Algorithm overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1127–1141. [Google Scholar] [CrossRef] [Green Version]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Pallavi, V.P.; Vaithiyanathan, V. Combined artificial neural network and genetic algorithm for cloud classification. Int. J. Eng. Technol. 2013, 5, 787–794. [Google Scholar]
- Fox, S.; Mendrok, J.; Eriksson, P.; Ekelund, R.; O’Shea, S.J.; Bower, K.N.; Baran, A.J.; Harlow, R.C.; Pickering, J.C. Airborne validation of radiative transfer modelling of ice clouds at millimetre and sub-millimetre wavelengths. Atmos. Meas. Tech. 2019, 12, 1599–1617. [Google Scholar] [CrossRef] [Green Version]
- Holl, G.; Eliasson, S.; Mendrok, J.; Buehler, S.A. SPARE-ICE: Synergistic ice water path from passive operational sensors. J. Geophys. Res.Atmos. 2014, 119, 1504–1523. [Google Scholar] [CrossRef]
- Jiménez, C.; Buehler, S.A.; Rydberg, B.; Eriksson, P.; Evans, K.F. Performance simulations for a submillimetre-wave satellite instrument to measure cloud ice. Q. J. R. Meteorol. Soc. 2007, 133, 129–149. [Google Scholar] [CrossRef]
- Evans, K.F.; Walter, S.J.; Heymsfield, A.J.; Deeter, M.N. Modeling of Submillimeter Passive Remote Sensing of Cirrus Clouds. J. Appl. Meteorol. 1998, 37, 184–205. [Google Scholar] [CrossRef] [Green Version]
- Evans, K.F.; Stephens, G.L. Microweve Radiative Transfer through Clouds Composed of Realistically Shaped Ice Crystals. Part II. Remote Sensing of Ice Clouds. J. Atmos. Sci. 1995, 52, 2058–2072. [Google Scholar] [CrossRef]
- Buehler, S.A.; Jiménez, C.; Evans, K.F.; Eriksson, P.; Rydberg, B.; Heymsfield, A.J.; Stubenrauch, C.J.; Lohmann, U.; Emde, C.; John, V.O.; et al. A concept for a satellite mission to measure cloud ice water path, ice particle size, and cloud altitude. Q. J. R. Meteorol. Soc. 2007, 133, 109–128. [Google Scholar] [CrossRef] [Green Version]
- Evans, K.F.; Walter, S.J.; Heymsfield, A.J.; Mcfarquhar, G.M. Submillimeter-wave cloud ice radiometer: Simulations of retrieval algorithm performance. J. Geophys. Res. Atmos. 2002, 107, AAC-2. [Google Scholar] [CrossRef]
- Evans, K.F.; Wang, J.R.; Racette, P.E.; Heymsfield, G.; Li, L. Ice Cloud Retrievals and Analysis with the Compact Scanning Submillimeter Imaging Radiometer and the Cloud Radar System during CRYSTAL FACE. J. Appl. Meteorol. 2005, 44, 839–859. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, C.; Eriksson, P.; Murtagh, D. First inversions of observed submillimeter limb sounding radiances by neural networks. J. Geophys. Res. Atmos. 2003, 108, 4791. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and PRACTICE; World Scientific: Singapore, 2000. [Google Scholar]
- Andrieu, C.; Thoms, J. A tutorial on adaptive MCMC. Stat. Comput. 2008, 18, 343–373. [Google Scholar] [CrossRef]
- Li, S.L.; Liu, L.; Gao, T.C.; Shi, L.H.; Qiu, S.; Hu, S. Radiation characteristics of the selected channels for cirrus remote sensing in terahertz waveband and the influence factors for the retrieval method. J. Infrared Millim. Waves 2018, 37, 60–65. [Google Scholar]
- Li, S.L.; Liu, L.; Gao, T.C.; Huang, W.; Hu, S. Sensitivity analysis of terahertz wave passive remote sensing of cirrus microphysical parameters. Acta Phy. Sin 2016, 65, 100–110. [Google Scholar] [CrossRef]
- Li, S.L.; Liu, L.; Gao, T.C.; Hu, S.; Huang, W. Retrieval method of cirrus microphysical parameters at terahertz wave based on multiple lookup tables. Acta Phy. Sin 2017, 66, 78–87. [Google Scholar] [CrossRef]
- Weng, C.; Liu, L.; Gao, T.; Hu, S.; Li, S.; Dou, F.; Shang, J. Multi-Channel Regression Inversion Method for Passive Remote Sensing of Ice Water Path in the Terahertz Band. Atmosphere 2019, 10, 437. [Google Scholar] [CrossRef] [Green Version]
- Evans, K.F.; Wang, J.R.; C Starr, D.; Heymsfield, G.; Li, L.; Tian, L.; Lawson, R.P.; Heymsfield, A.J.; Bansemer, A. Ice hydrometeor profile retrieval algorithm for high-frequency microwave radiometers: Application to the CoSSIR instrument during TC4. Atmos. Meas. Tech. 2012, 5, 2277–2306. [Google Scholar] [CrossRef] [Green Version]
- Mendrok, J.; Picard, R.H.; Baron, P.; Comeron, A.; Schäfer, K.; Kasai, Y.; Amodeo, A.; van Weele, M. Studying the potential of terahertz radiation for deriving ice cloud microphysical information. In Remote Sensing of Clouds and the Atmosphere XIII; International Society for Optics and Photonics: Cardiff, UK, 2008. [Google Scholar] [CrossRef]
- Fox, S.; Lee, C.; Moyna, B.; Philipp, M.; Rule, I.; Rogers, S.; King, R.; Oldfield, M.; Rea, S.; Henry, M.; et al. ISMAR: An airborne submillimetre radiometer. Atmos. Meas. Tech. 2017, 10, 477–490. [Google Scholar] [CrossRef]
- Kangas, V.; D’Addio, S.; Betto, M. Metop Second Generation microwave sounding and microware imaging missions. In Proceedings of the 2012 EUMETSAT Meteorological Satellite Conference, Sopot, Poland, 3–7 September 2012. [Google Scholar]
- Eriksson, P.; Buehler, S.A.; Davis, C.P.; Emde, C.; Lemke, O. ARTS, the atmospheric radiative transfer simulator, version 2. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1551–1558. [Google Scholar] [CrossRef] [Green Version]
- Buehler, S.A.; Mendrok, J.; Eriksson, P.; Perrin, A.; Larsson, R.; Lemke, O. ARTS, the Atmospheric Radiative Transfer Simulator—version 2.2, the planetary toolbox edition. Geosci. Model Dev. 2018, 11, 1537–1556. [Google Scholar] [CrossRef] [Green Version]
- Anderson, G.P.; Clough, S.A.; Kneizys, F.X.; Chetwynd, J.H.; Shettle, E.P. AFGL Atmospheric Constituent Profiles (0–120 km); AFGL-TR-86-0110; Optical Physics Division, Air Force Geophysics Laboratory: Hanscom Air Force Base, MA, USA, 1986. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Chris Benner, D.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef] [Green Version]
- Geer, A.J.; Baordo, F. Improved scattering radiative transfer for frozen hydrometeors at microwave frequencies. Atmos. Meas. Tech. 2014, 7, 1839–1860. [Google Scholar] [CrossRef] [Green Version]
- Brath, M.; Fox, S.; Eriksson, P.; Harlow, R.C.; Burgdorf, M.; Buehler, S.A. Retrieval of an ice water path over the ocean from ISMAR and MARSS millimeter and submillimeter brightness temperatures. Atmos. Meas. Tech. 2018, 11, 611–632. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Buehler, S.A.; Brath, M.; Liu, H.; Dong, X. Ensemble Optimization Retrieval Algorithm of Hydrometeor Profiles for the Ice Cloud Imager Submillimeter-Wave Radiometer. J. Geophys. Res. Atmos. 2018, 123, 4594–4612. [Google Scholar] [CrossRef]
- Mie, G. Beitrage Zur Optik Trüber Medien, Speziell Kolloidaler Metallosungen. Ann. Der Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Hergert, W.; Wriedt, T. The Mie Theory: Basics and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 53–71. [Google Scholar] [CrossRef] [Green Version]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Oxford, UK, 1975. [Google Scholar]
- De Jong, A.K. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Longman Press Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]






| Center Frequency (GHz) | Center Wavelength (μm) | Frequency Offset (GHz) | Channel Characteristics |
|---|---|---|---|
| 118.75 | 2526.3 | ±1.1, ±1.5, ±2.1, ±3.0, ±5.0 | oxygen |
| 157.05 | 1910.2 | ±2.6 | window |
| 183.31 | 1636.6 | ±1.0, ± 3.0, ±7.0 | water vapor |
| 243.20 | 1233.6 | ±2.5 | window |
| 325.15 | 922.7 | ±1.5, ±3.5, ±9.5 | water vapor |
| 424.70 | 706.3 | ±1.0, ±1.5, ±4.0 | oxygen |
| 448.0 | 669.6 | ±1.4, ±3.0, ±7.2 | water vapor |
| 664.0 | 451.8 | ±4.2 | window |
| 874.4 | 343.1 | ±6.0 | window |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Weng, C.; Li, S.; Husi, L.; Hu, S.; Dong, P. Passive Remote Sensing of Ice Cloud Properties at Terahertz Wavelengths Based on Genetic Algorithm. Remote Sens. 2021, 13, 735. https://doi.org/10.3390/rs13040735
Liu L, Weng C, Li S, Husi L, Hu S, Dong P. Passive Remote Sensing of Ice Cloud Properties at Terahertz Wavelengths Based on Genetic Algorithm. Remote Sensing. 2021; 13(4):735. https://doi.org/10.3390/rs13040735
Chicago/Turabian StyleLiu, Lei, Chensi Weng, Shulei Li, Letu Husi, Shuai Hu, and Pingyi Dong. 2021. "Passive Remote Sensing of Ice Cloud Properties at Terahertz Wavelengths Based on Genetic Algorithm" Remote Sensing 13, no. 4: 735. https://doi.org/10.3390/rs13040735
APA StyleLiu, L., Weng, C., Li, S., Husi, L., Hu, S., & Dong, P. (2021). Passive Remote Sensing of Ice Cloud Properties at Terahertz Wavelengths Based on Genetic Algorithm. Remote Sensing, 13(4), 735. https://doi.org/10.3390/rs13040735