Application of Denoising CNN for Noise Suppression and Weak Signal Extraction of Lunar Penetrating Radar Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Initial CH-2B LPR Data
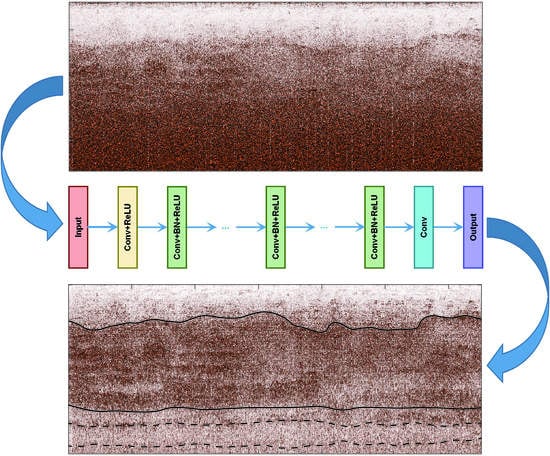
2.2. Methodology of Denoising CNN
3. Results
3.1. CNN Training
3.2. Model Denoising Test
3.3. Denoising and Weak Signal Extraction of LPR Data
3.4. The Subsurface Sandwich Structure at CE-4 Landing Site
4. Discussions
4.1. Detailed and Quantitative Comparisons of Filtering Methods
4.2. Why the CNN Filter Performs Better?
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Processing | Details |
|---|---|
| Traces amending | Adjusting the longitudinal displacement of traces, based on the phase of a strong reflection event. |
| Traces selecting | The rover might stop at some points on the way to collect other scientific data. But LPR never stops measurement, which resulted in the repeated acquisition of multiple traces at the same location. We average the repeated traces. |
| Time lag adjustment | There is a 28.203 ns delay for the start time of the transmitting antenna compared to the receiving antenna. |
| Attenuation compensation | Conducting SEC makes deep information more visible. |
| Background removal | Removing the average background data. |
References
- Liu, J.; Ren, X.; Yan, W.; Li, C.; Zhang, H.; Jia, Y.; Zeng, X.; Chen, W.; Gao, X.; Liu, D.; et al. Descent trajectory reconstruction and landing site positioning of Chang’E-4 on the lunar farside. Nat. Commun. 2019, 10, 4229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haruyama, J.; Ohtake, M.; Matsunaga, T.; Morota, T.; Honda, C.; Yokota, Y.; Abe, M.; Ogawa, Y.; Miyamoto, H.; Iwasaki, A.; et al. Long-lived volcanism on the lunar farside revealed by SELENE Terrain Camera. Science 2009, 323, 905–908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stuart-Alexander, D.E. Geologic Map of the Central Far Side of the Moon I-1047. In US Geological Survey; 1978. Available online: https://pubs.er.usgs.gov/publication/i1047 (accessed on 4 December 2019). [CrossRef]
- Head, J.W., III; Fassett, C.I.; Kadish, S.J.; Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E. Global distribution of large lunar craters: Implications for resurfacing and impactor populations. Science 2010, 329, 1504–1507. [Google Scholar] [CrossRef]
- Garrick-Bethell, I.; Zuber, M.T. Elliptical structure of the lunar South Pole-Aitken basin. Icarus 2009, 204, 399–408. [Google Scholar] [CrossRef]
- Pascket, J.H.; Hiesinger, H.; van der Bogert, C.H. Lunar far side volcanism in and around the south pole Aitken basin. Icarus 2018, 299, 538–562. [Google Scholar] [CrossRef]
- Huang, J.; Xiao, Z.; Flahaut, J.; Martinot, M.; Head, J.; Xiao, X.; Xie, M.; Xiao, L. Geological characteristics of Von Kármán crater, northwesternSouth PoleAitken basin: Chang’E-4 landing site region. J. Geophys. Res. Planets 2018, 123, 1684–1700. [Google Scholar] [CrossRef] [Green Version]
- Lai, J.; Xu, Y.; Bugiolacchi, R.; Meng, X.; Xiao, L.; Xie, M.; Liu, B.; Di, K.; Zhang, X.; Zhou, B.; et al. First look by the Yutu-2 rover at the deep subsurface structure at the lunar farside. Nat. Commun. 2020, 11, 3426. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, B.; Lin, Y.; Zhu, M.; Song, H.; Dong, Z.; Gao, Y.; Di, K.; Yang, W.; Lin, H.; et al. Lunar regolith and substructure at Chang’E-4 landing site in South Pole-Aitken basin. Nat. Astron. 2020. [Google Scholar] [CrossRef]
- Zhang, L.; Li, J.; Zeng, Z.; Xu, Y.; Liu, C.; Chen, S. Stratigraphy of the Von Kármán Crater based on Chang’E-4 lunar penetrating radar data. Geophys. Res. Lett. 2020, 47, e2020GL088680. [Google Scholar] [CrossRef]
- Li, C.; Su, Y.; Pettinelli, E.; Xing, S.; Ding, C.; Liu, J.; Ren, X.; Lauro, S.E.; Soldovieri, F.; Zeng, X.; et al. The Moon’s farside shallow subsurface structure unveiled by Chang’E-4 lunar penetrating radar. Sci. Adv. 2020, 6, eaay6898. [Google Scholar] [CrossRef] [Green Version]
- Gou, S.; Yue, Z.; Di, K.; Cai, Z.; Liu, Z.; Niu, S. Absolute model age of lunar Finsen crater and geologic implications. Icarus 2021, 354, 115829. [Google Scholar] [CrossRef]
- Ding, C.; Xiao, Z.; Wu, B.; Li, Y.; Prieur, N.C.; Cai, Y.; Su, Y.; Cui, J. Fragments delivered by secondary craters at the Chang’E-4 landing site. Geophys. Res. Lett. 2020, 47, e2020GL087361. [Google Scholar] [CrossRef]
- Di, K.; Zhu, M.; Yue, Z.; Lin, Y.; Wan, W.; Liu, Z.; Gou, S.; Liu, B.; Peng, M.; Wang, Y. Topographic evolution of Von Kármán crater revealed by the lunar rover Yutu-2. Geophys. Res. Lett. 2019, 46, 12764–12770. [Google Scholar] [CrossRef]
- Hu, X.; Ma, P.; Yang, Y.; Zhu, M.; Jiang, T.; Lucey, P.G.; Sun, L.; Zhang, H.; Li, C.; Xu, R.; et al. Mineral abundances inferred from in situ reflectance measurements of Chang’E-4 landing site in South Pole-Aitken basin. Geophys. Res. Lett. 2019, 46, 9439–9447. [Google Scholar] [CrossRef]
- Qiao, L.; Ling, Z.; Fu, X.; Li, B. Geological characterization of the Chang’e-4 landing area on the lunar farside. Icarus 2019, 333, 37–51. [Google Scholar] [CrossRef]
- Ling, Z.; Qiao, L.; Liu, C.; Cao, H.; Bi, X.; Lu, X.; Zhang, J.; Fu, X.; Li, B.; Liu, J. Composition, mineralogy and chronology of mare basalts and non-mare materials in Von Kármán crater: Landing site of the Chang’E-4 mission. Planet. Space Sci. 2019, 179. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Liu, B.; Ren, X.; Liu, J.; He, Z.; Zuo, W.; Zeng, X.; Xu, R.; Tan, X.; et al. Chang’E-4 initial spectroscopic identification of lunar far side mantle–derived materials. Nature 2019, 569, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Gou, S.; Di, K.; Yue, Z.; Liu, Z.; He, Z.; Xu, R.; Lin, H.; Liu, B.; Peng, M.; Wan, W.; et al. Lunar deep materials observed by Chang’e-4 rover. Earth Planet. Sci. Lett. 2019, 528, 115829. [Google Scholar] [CrossRef]
- Gou, S.; Yue, Z.; Di, K.; Wang, J.; Wan, W.; Liu, Z.; Liu, B.; Peng, M.; Wang, Y.; He, Z.; et al. Impact melt breccia and surrounding regolith measured by Chang’e-4 rover. Earth Planet. Sci. Lett. 2020, 544, 116378. [Google Scholar] [CrossRef]
- Ma, P.; Sun, Y.; Zhu, M.; Yang, Y.; Hu, X.; Jiang, T.; Zhang, H.; Lucey, P.G.; Xu, R.; Li, C.; et al. A plagioclase-rich rock measured by Yutu-2 rover in Von Kármán crater on the far side of the Moon. Icarus 2020, 350, 113901. [Google Scholar] [CrossRef]
- Jia, Y.; Zou, Y.; Ping, J.; Xue, C.; Yan, J.; Ning, Y. The Scientific Objectives and Payloads of Chang’E-4 Mission. Planet. Space Sci. 2018, 38, 118–130. [Google Scholar] [CrossRef]
- Fang, G.; Zhou, B.; Ji, Y.; Zhang, Q.; Shen, S.; Li, Y.; Guan, H.; Tang, C.; Gao, Y.; Lu, W.; et al. Lunar Penetrating Radar onboard the Chang’e-3 mission. Res. Astron. Astrophys. 2014, 14, 1607–1622. [Google Scholar] [CrossRef]
- Su, Y.; Fang, G.; Feng, J.; Xing, S.; Ji, Y.; Zhou, B.; Gao, Y.; Li, H.; Dai, S.; Xiao, Y.; et al. Data processing and initial results of Chang’e-3 lunar penetrating radar. Res. Astron. Astrophys. 2014, 14, 1623–1632. [Google Scholar] [CrossRef]
- Fa, W.; Zhu, M.; Liu, T.; Plescia, J.B. Regolith stratigraphy at the Chang’E-3 landing site as seen by lunar penetrating radar. Geophys. Res. Lett. 2015, 42, 10179–10187. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, W.; Hu, S.; Lin, Y.; Fang, G.; Li, C.; Peng, W.; Zhu, S.; He, Z.; Zhou, B.; et al. Volcanic history of the Imbrium basin: A close-up view from the lunar rover Yutu. Proc. Natl. Acad. Sci. USA 2015, 112, 5342–5347. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zeng, Z.; Li, J.; Huang, L.; Huo, Z.; Zhang, J.; Huai, N. A Story of Regolith Told by Lunar Penetrating Radar. Icarus 2019, 321, 148–160. [Google Scholar] [CrossRef]
- Xiao, L.; Zhu, P.; Fang, G.; Xiao, Z.; Zhu, Y.; Zhao, J.; Zhao, N.; Yuan, Y.; Qiao, L.; Zhang, X.; et al. A young multilayering terrane of the northern Mare Imbrium revealed by Chang’E-3 mission. Science 2015, 347, 1226–1229. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Xiao, Z.; Su, Y.; Zhao, J.; Cui, J. Compositional variations along the route of Chang’e-3 Yutu rover revealed by the lunar penetrating radar. Prog. Earth Planet. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Li, J.; Huang, L.; Huo, Z.; Wang, K.; Zhang, J. Parameter Estimation of Lunar Regolith from Lunar Penetrating Radar Data. Sensors 2018, 18, 2907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, B.; Wang, D.; Zhang, L.; Zeng, Z. Rock Location and Quantitative Analysis of Regolith at the Chang’e 3 Landing Site Based on Local Similarity Constraint. Remote Sens. 2019, 11, 530. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Li, C.; Zhang, J.; Wu, X.; Liu, Y.; Zou, Y. Rock Location and Property Analysis of Lunar Regolith at Chang’E-4 Landing Site Based on Local Correlation and Semblance Analysis. Remote Sens. 2021, 13, 48. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, B.; Jia, Z.; Xu, Y.; Huang, L. The Subsurface Structure on the CE-3 Landing Site: LPR CH-1 Data Processing by Shearlet Transform. Pure Appl. Geophys. 2020, 177, 3459–3474. [Google Scholar] [CrossRef]
- Feng, J.; Su, Y.; Ding, C.; Xing, S.; Dai, S.; Zou, Y. Dielectric properties estimation of the lunar regolith at CE-3 landing site using lunar penetrating radar data. Icarus 2017, 284, 424–430. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Li, J.; Lin, J.; Hu, Y.; Wang, X.; Sun, X. Simulation of the lunar regolith and lunar penetrating radar data processing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 655–663. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, Z.; Li, J.; Lin, J.; Zhang, J. Lunar Penetrating Radar Data Processing and Analysis Based on CEEMD. In Proceedings of the 17th International Conference on Ground Penetrating Radar (GPR), Rapperswil, Switzerland, 18–21 June 2018; pp. 635–638. [Google Scholar]
- Zhang, J.; Zeng, Z.; Zhang, L.; Lu, Q.; Wang, K. Application of Mathematical Morphological Filtering to Improve the Resolution of Chang’E-3 Lunar Penetrating Radar Data. Remote Sens. 2019, 11, 524. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Feng, X.; Zhou, H.; Lu, Q.; Liu, C.; Zeng, Z.; Li, J.; Liang, W. Date Processing for Lunar Penetrating Radar of Chang’E-4 based on Variational Mode Decomposition. In Proceedings of the 18th International Conference on Ground Penetrating Radar (GPR), Golden, CO, USA, 14–19 June 2020; pp. 424–427. [Google Scholar]
- Hubel, D.H.; Wiesel, T.N. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 1968, 195, 1. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proceed. IEEE 1998, 86, 11. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Adv. Neural inf. Process. Syst. 2012, 1097–1105. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 7. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, N.E.; Shen, Z.; Long, S.; Wu, M.; Shih, H.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Seri. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wiggins, R. Minimum entropy deconvolution. Geoexploration 1978, 16, 21–35. [Google Scholar] [CrossRef]
- Wu, H.; Barba, J. Minimum entropy restoration of star field images. IEEE Trans. Syst. Man Cybernet. 1998, 28, 227–231. [Google Scholar] [CrossRef]
- Xu, X.; Miller, E.L.; Rappaport, C.R. Minimum Entropy Regularization in Frequency-Wavenumber Migration to Localize Subsurface Objects. IEEE Trans. Geosci. Remote Sens. 2003, 41, 8. [Google Scholar] [CrossRef]
- Stockwell, R.G.; Man-sinha, L.; Lowe, R.P. Localization of the Complex Spectrum: The S Transform. IEEE Trans. Signal Process. 1996, 44, 998–1001. [Google Scholar] [CrossRef]
- Dong, Z.; Fang, G.; Zhao, D.; Zhou, B.; Gao, Y.; Ji, Y. Dielectric Properties of Lunar Subsurface Materials. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Lai, J.; Xu, Y.; Zhang, X.; Xiao, L.; Yan, Q.; Meng, X.; Zhou, B.; Dong, Z.; Zhao, D. Comparison of dielectric properties and structure of lunar regolith at Chang’e-3 and Chang’e-4 landing sites revealed by ground-penetrating radar. Geophys. Res. Lett. 2019, 46, 12783–12793. [Google Scholar] [CrossRef]
- Lai, J.; Xu, Y.; Zhang, X.; Tang, Z. Structural analysis of lunar subsurface with Chang’E-3 lunar penetrating radar. Planet. Space Sci. 2016, 120, 96–102. [Google Scholar] [CrossRef]
- Dong, Z.; Feng, X.; Zhou, H.; Liu, C.; Zeng, Z.; Li, J.; Liang, W. Properties Analysis of Lunar Regolith at Chang’E-4 Landing Site Based on 3D Velocity Spectrum of Lunar Penetrating Radar. Remote Sens. 2020, 12, 629. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.; Ding, C.; Xie, M.; Cai, Y.; Cui, J.; Zhang, K.; Wang, J. Ejecta from the Orientale basin at the Chang’E-4 landing site. Geophys. Res. Lett. 2021, e2020GL090935. [Google Scholar] [CrossRef]














| Images | CNN Filtering | Band-Pass and Mean Filtering |
|---|---|---|
| Figure 14d,e | 1.9075 × 106 | 2.1871 × 106 |
| Figure 15a | 5.7698 × 104 | 7.3160 × 104 |
| Figure 15b | 6.3342 × 104 | 7.4902 × 104 |
| Figure 15c | 5.5177 × 104 | 7.0545 × 104 |
| CNN Filtering | Band-Pass and Mean Filtering |
|---|---|
| 1.9278 × 103 | 2.4477 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W. Application of Denoising CNN for Noise Suppression and Weak Signal Extraction of Lunar Penetrating Radar Data. Remote Sens. 2021, 13, 779. https://doi.org/10.3390/rs13040779
Zhou H, Feng X, Dong Z, Liu C, Liang W. Application of Denoising CNN for Noise Suppression and Weak Signal Extraction of Lunar Penetrating Radar Data. Remote Sensing. 2021; 13(4):779. https://doi.org/10.3390/rs13040779
Chicago/Turabian StyleZhou, Haoqiu, Xuan Feng, Zejun Dong, Cai Liu, and Wenjing Liang. 2021. "Application of Denoising CNN for Noise Suppression and Weak Signal Extraction of Lunar Penetrating Radar Data" Remote Sensing 13, no. 4: 779. https://doi.org/10.3390/rs13040779
APA StyleZhou, H., Feng, X., Dong, Z., Liu, C., & Liang, W. (2021). Application of Denoising CNN for Noise Suppression and Weak Signal Extraction of Lunar Penetrating Radar Data. Remote Sensing, 13(4), 779. https://doi.org/10.3390/rs13040779