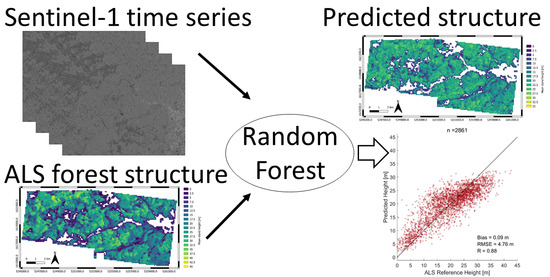
Potential of Sentinel-1 C-Band Time Series to Derive Structural Parameters of Temperate Deciduous Forests
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Area
2.2. ALS Data
2.3. ALS Data Processing
2.3.1. Stand Height
2.3.2. Fractional Cover
2.4. Sentinel-1 Data
2.4.1. Radiometric Terrain Flattened Gamma Nought (Backscatter)
2.4.2. Cross Ratio
2.4.3. Coherence
2.4.4. Seasonal and Spatial Aggregation of SAR Data
2.4.5. Backscatter-Incidence Angle Slope
2.5. Structure Prediction Model
2.6. Experimental Design
3. Results
3.1. ALS Metrics Aggregation
3.2. Prediction of ALS Metrics
3.2.1. Stand Height
3.2.2. Fractional Cover
3.3. Stratified Training Sets
3.3.1. Stand Height
3.3.2. Fractional Cover
3.4. Predictive Power of Coherence
3.5. Model Transfer
4. Discussion
4.1. Prediction of Stand Height
4.2. Prediction of Fractional Cover
4.3. Predictive Power of Coherence
4.4. Model Transfer
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


Appendix B




References
- Chuvieco, E.; Yue, C.; Heil, A.; Mouillot, F.; Alonso-Canas, I.; Padilla, M.; Pereira, J.M.; Oom, D.; Tansey, K. A new global burned area product for climate assessment of fire impacts. Glob. Ecol. Biogeogr. 2016, 25, 619–629. [Google Scholar] [CrossRef] [Green Version]
- Giglio, L.; Randerson, J.T.; Van Der Werf, G.R. Analysis of daily, monthly, and annual burned area using the fourth-generation global fire emissions database (GFED4). J. Geophys. Res. Biogeosci. 2013, 118, 317–328. [Google Scholar] [CrossRef] [Green Version]
- Kasischke, E.S.; Bruhwiler, L.P. Emissions of carbon dioxide, carbon monoxide, and methane from boreal forest fires in 1998. J. Geophys. Res. Atmos. 2002, 107, FFR2-1–FFR2-14. [Google Scholar] [CrossRef] [Green Version]
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; Collatz, G.; Mu, M.; Kasibhatla, P.S.; Morton, D.C.; DeFries, R.; Jin, Y.; van Leeuwen, T.T. Global fire emissions and the contribution of deforestation, savanna, forest, agricultural, and peat fires (1997–2009). Atmos. Chem. Phys. 2010, 10, 11707–11735. [Google Scholar] [CrossRef] [Green Version]
- Vinogradova, A.; Smirnov, N.; Korotkov, V.; Romanovskaya, A. Forest fires in Siberia and the Far East: Emissions and atmospheric transport of black carbon to the Arctic. Atmos. Ocean. Opt. 2015, 28, 566–574. [Google Scholar] [CrossRef]
- Langenfelds, R.; Francey, R.; Pak, B.; Steele, L.; Lloyd, J.; Trudinger, C.; Allison, C. Interannual growth rate variations of atmospheric CO2 and its δ13C, H2, CH4, and CO between 1992 and 1999 linked to biomass burning. Glob. Biogeochem. Cycles 2002, 16, 21-1–21-22. [Google Scholar] [CrossRef]
- Simpson, I.J.; Rowland, F.S.; Meinardi, S.; Blake, D.R. Influence of biomass burning during recent fluctuations in the slow growth of global tropospheric methane. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Abatzoglou, J.T.; Williams, A.P. Impact of anthropogenic climate change on wildfire across western US forests. Proc. Natl. Acad. Sci. USA 2016, 113, 11770–11775. [Google Scholar] [CrossRef] [Green Version]
- Müller, M.M.; Vilà-Vilardell, L.; Vacik, H. Towards an integrated forest fire danger assessment system for the European Alps. Ecol. Inform. 2020, 60, 101151. [Google Scholar] [CrossRef]
- Wastl, C.; Schunk, C.; Lüpke, M.; Cocca, G.; Conedera, M.; Valese, E.; Menzel, A. Large-scale weather types, forest fire danger, and wildfire occurrence in the Alps. Agric. For. Meteorol. 2013, 168, 15–25. [Google Scholar] [CrossRef]
- Müller, M.M.; Vacik, H.; Valese, E. Anomalies of the Austrian forest fire regime in comparison with other Alpine countries: A research note. Forests 2015, 6, 903–913. [Google Scholar] [CrossRef]
- Arpaci, A.; Eastaugh, C.S.; Vacik, H. Selecting the best performing fire weather indices for Austrian ecoregions. Theor. Appl. Climatol. 2013, 114, 393–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J.; Williamson, G.J.; Bowman, D.M. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 2015, 6, 1–11. [Google Scholar] [CrossRef]
- Arpaci, A.; Malowerschnig, B.; Sass, O.; Vacik, H. Using multi variate data mining techniques for estimating fire susceptibility of Tyrolean forests. Appl. Geogr. 2014, 53, 258–270. [Google Scholar] [CrossRef]
- Vacik, H.; Arndt, N.; Arpaci, A.; Koch, V.; Müller, M.; Gossow, H. Characterisation of forest fires in Austria. Austrian J. For. Sci. 2011, 128, 1–31. [Google Scholar]
- Müller, M.M.; Vacik, H.; Diendorfer, G.; Arpaci, A.; Formayer, H.; Gossow, H. Analysis of lightning-induced forest fires in Austria. Theor. Appl. Climatol. 2013, 111, 183–193. [Google Scholar] [CrossRef] [Green Version]
- Chuvieco, E.; Aguado, I.; Yebra, M.; Nieto, H.; Salas, J.; Martín, M.P.; Vilar, L.; Martínez, J.; Martín, S.; Ibarra, P.; et al. Development of a framework for fire risk assessment using remote sensing and geographic information system technologies. Ecol. Model. 2010, 221, 46–58. [Google Scholar] [CrossRef]
- Chuvieco, E.; Allgöwer, B.; Salas, J. Integration of physical and human factors in fire danger assessment. In Wildland Fire Danger Estimation and Mapping: The Role of Remote Sensing Data; World Scientific: Singapore, 2003; pp. 197–218. [Google Scholar]
- García, M.; Riaño, D.; Chuvieco, E.; Salas, J.; Danson, F.M. Multispectral and LiDAR data fusion for fuel type mapping using Support Vector Machine and decision rules. Remote Sens. Environ. 2011, 115, 1369–1379. [Google Scholar] [CrossRef]
- Domingo, D.; de la Riva, J.; Lamelas, M.T.; García-Martín, A.; Ibarra, P.; Echeverría, M.; Hoffrén, R. Fuel Type Classification Using Airborne Laser Scanning and Sentinel 2 Data in Mediterranean Forest Affected by Wildfires. Remote Sens. 2020, 12, 3660. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Hollaus, M.; Mücke, W.; Höfle, B.; Dorigo, W.; Pfeifer, N.; Wagner, W.; Bauerhansl, C.; Regner, B. Tree species classification based on full-waveform airborne laser scanning data. In Proceedings of the SilviLaser, College Station, TX, USA, 14–16 October 2009. [Google Scholar]
- Korpela, I.; Ørka, H.O.; Maltamo, M.; Tokola, T.; Hyyppä, J. Tree species classification using airborne LiDAR–effects of stand and tree parameters, downsizing of training set, intensity normalization, and sensor type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef] [Green Version]
- Hill, R.; Broughton, R.K. Mapping the understorey of deciduous woodland from leaf-on and leaf-off airborne LiDAR data: A case study in lowland Britain. ISPRS J. Photogramm. Remote Sens. 2009, 64, 223–233. [Google Scholar] [CrossRef]
- Morsdorf, F.; Mårell, A.; Koetz, B.; Cassagne, N.; Pimont, F.; Rigolot, E.; Allgöwer, B. Discrimination of vegetation strata in a multi-layered Mediterranean forest ecosystem using height and intensity information derived from airborne laser scanning. Remote Sens. Environ. 2010, 114, 1403–1415. [Google Scholar] [CrossRef] [Green Version]
- Leiterer, R.; Torabzadeh, H.; Furrer, R.; Schaepman, M.E.; Morsdorf, F. Towards automated characterization of canopy layering in mixed temperate forests using airborne laser scanning. Forests 2015, 6, 4146–4167. [Google Scholar] [CrossRef] [Green Version]
- Crespo-Peremarch, P.; Tompalski, P.; Coops, N.C.; Ruiz, L.Á. Characterizing understory vegetation in Mediterranean forests using full-waveform airborne laser scanning data. Remote Sens. Environ. 2018, 217, 400–413. [Google Scholar] [CrossRef]
- Maltamo, M.; Hyyppä, J.; Malinen, J. A comparative study of the use of laser scanner data and field measurements in the prediction of crown height in boreal forests. Scand. J. For. Res. 2006, 21, 231–238. [Google Scholar] [CrossRef]
- Vauhkonen, J. Estimating crown base height for Scots pine by means of the 3D geometry of airborne laser scanning data. Int. J. Remote Sens. 2010, 31, 1213–1226. [Google Scholar] [CrossRef]
- Popescu, S.C.; Zhao, K. A voxel-based lidar method for estimating crown base height for deciduous and pine trees. Remote Sens. Environ. 2008, 112, 767–781. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- Hollaus, M. 3D Point clouds for forestry applications. Österreichische Z. Vermess. Geoinf. VGI 2015, 103, 138–150. [Google Scholar]
- Fisher, A.; Armston, J.; Goodwin, N.; Scarth, P. Modelling canopy gap probability, foliage projective cover and crown projective cover from airborne lidar metrics in Australian forests and woodlands. Remote Sens. Environ. 2020, 237, 111520. [Google Scholar] [CrossRef]
- Kellndorfer, J.M.; Pierce, L.E.; Dobson, M.C.; Ulaby, F.T. Toward consistent regional-to-global-scale vegetation characterization using orbital SAR systems. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1396–1411. [Google Scholar] [CrossRef]
- Dostálová, A.; Wagner, W.; Milenković, M.; Hollaus, M. Annual seasonality in Sentinel-1 signal for forest mapping and forest type classification. Int. J. Remote Sens. 2018, 39, 7738–7760. [Google Scholar] [CrossRef]
- Rüetschi, M.; Schaepman, M.E.; Small, D. Using multitemporal sentinel-1 c-band backscatter to monitor phenology and classify deciduous and coniferous forests in northern switzerland. Remote Sens. 2018, 10, 55. [Google Scholar] [CrossRef] [Green Version]
- Kaasalainen, S.; Holopainen, M.; Karjalainen, M.; Vastaranta, M.; Kankare, V.; Karila, K.; Osmanoglu, B. Combining lidar and synthetic aperture radar data to estimate forest biomass: Status and prospects. Forests 2015, 6, 252–270. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height estimation from shuttle radar topography mission and national elevation datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Praks, J.; Antropov, O.; Hallikainen, M.T. LIDAR-aided SAR interferometry studies in boreal forest: Scattering phase center and extinction coefficient at X-and L-band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3831–3843. [Google Scholar] [CrossRef]
- Lei, Y.; Siqueira, P.; Torbick, N.; Ducey, M.; Chowdhury, D.; Salas, W. Generation of Large-Scale Moderate-Resolution Forest Height Mosaic With Spaceborne Repeat-Pass SAR Interferometry and Lidar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 770–787. [Google Scholar] [CrossRef]
- Siqueira, P.; Hensley, S.; Chapman, B.; Ahmed, R. Combining lidar and InSAR observations over the harvard and duke forests for making wide area maps of vegetation height. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 5, pp. 538–541. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Bollandsås, O.M.; Næsset, E.; Weydahl, D.J. Deriving forest monitoring variables from X-band InSAR SRTM height. Can. J. Remote Sens. 2010, 36, 68–79. [Google Scholar] [CrossRef]
- Soja, M.J.; Persson, H.; Ulander, L.M. Estimation of forest height and canopy density from a single InSAR correlation coefficient. IEEE Geosci. Remote Sens. Lett. 2014, 12, 646–650. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Hyyppä, J.; Karjalainen, M.; Nurminen, K.; Karila, K.; Vastaranta, M.; Kankare, V.; Kaartinen, H.; Holopainen, M.; Honkavaara, E.; et al. Comparison of laser and stereo optical, SAR and InSAR point clouds from air-and space-borne sources in the retrieval of forest inventory attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar] [CrossRef] [Green Version]
- Lucas, R.M.; Cronin, N.; Moghaddam, M.; Lee, A.; Armston, J.; Bunting, P.; Witte, C. Integration of radar and Landsat-derived foliage projected cover for woody regrowth mapping, Queensland, Australia. Remote Sens. Environ. 2006, 100, 388–406. [Google Scholar] [CrossRef] [Green Version]
- Morin, D.; Planells, M.; Guyon, D.; Villard, L.; Mermoz, S.; Bouvet, A.; Thevenon, H.; Dejoux, J.F.; Le Toan, T.; Dedieu, G. Estimation and mapping of forest structure parameters from open access satellite images: Development of a generic method with a study case on coniferous plantation. Remote Sens. 2019, 11, 1275. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Mathieu, R.; Naidoo, L.; Levick, S.R.; Smit, I.P.; Asner, G.P.; Schmullius, C. Assessment of the mapping of fractional woody cover in southern African savannas using multi-temporal and polarimetric ALOS PALSAR L-band images. Remote Sens. Environ. 2015, 166, 138–153. [Google Scholar] [CrossRef] [Green Version]
- Dostálová, A.; Lang, M.; Ivanovs, J.; Waser, L.T.; Wagner, W. European Wide Forest Classification Based on Sentinel-1 Data. Remote Sens. 2021, 13, 337. [Google Scholar] [CrossRef]
- Urban, M.; Heckel, K.; Berger, C.; Schratz, P.; Smit, I.P.; Strydom, T.; Baade, J.; Schmullius, C. Woody cover mapping in the savanna ecosystem of the Kruger National Park using Sentinel-1 C-Band time series data. Koedoe 2020, 62, 6. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Karjalainen, M.; Kankare, V.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Prediction of plot-level forest variables using TerraSAR-X stereo SAR data. Remote Sens. Environ. 2012, 117, 338–347. [Google Scholar] [CrossRef]
- Solimini, D. Understanding Earth Observation; Springer International Publishing: Basel, Switzerland, 2016; pp. 1–703. [Google Scholar]
- Erdody, T.L.; Moskal, L.M. Fusion of LiDAR and imagery for estimating forest canopy fuels. Remote Sens. Environ. 2010, 114, 725–737. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Kazakova, A.N.; Coops, N.C.; Moskal, L.M. Estimation of forest structure and canopy fuel parameters from small-footprint full-waveform LiDAR data. Int. J. Wildland Fire 2014, 23, 224–233. [Google Scholar] [CrossRef] [Green Version]
- Jennings, S.; Brown, N.; Sheil, D. Assessing forest canopies and understorey illumination: Canopy closure, canopy cover and other measures. Forestry 1999, 72, 59–74. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Jenkins, M.J.; Hebertson, E.; Page, W.; Jorgensen, C.A. Bark beetles, fuels, fires and implications for forest management in the Intermountain West. For. Ecol. Manag. 2008, 254, 16–34. [Google Scholar] [CrossRef]
- Riaño, D.; Valladares, F.; Condés, S.; Chuvieco, E. Estimation of leaf area index and covered ground from airborne laser scanner (Lidar) in two contrasting forests. Agric. For. Meteorol. 2004, 124, 269–275. [Google Scholar] [CrossRef]
- Morsdorf, F.; Kötz, B.; Meier, E.; Itten, K.; Allgöwer, B. Estimation of LAI and fractional cover from small footprint airborne laser scanning data based on gap fraction. Remote Sens. Environ. 2006, 104, 50–61. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Hanssen, K.H.; Christiansen, E. Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sens. Environ. 2006, 102, 364–376. [Google Scholar] [CrossRef]
- Holmgren, J.; Johansson, F.; Olofsson, K.; Olsson, H.; Glimskär, A. Estimation of crown coverage using airborne laser scanning. In Proceedings of the SilviLaser 2008, Scotland, UK, 17–19 September 2008; pp. 50–57. [Google Scholar]
- Askne, J.I.; Fransson, J.E.; Santoro, M.; Soja, M.J.; Ulander, L.M. Model-based biomass estimation of a hemi-boreal forest from multitemporal TanDEM-X acquisitions. Remote Sens. 2013, 5, 5574–5597. [Google Scholar] [CrossRef] [Green Version]
- Solberg, S.; Astrup, R.; Breidenbach, J.; Nilsen, B.; Weydahl, D. Monitoring spruce volume and biomass with InSAR data from TanDEM-X. Remote Sens. Environ. 2013, 139, 60–67. [Google Scholar] [CrossRef]
- Kugler, F.; Schulze, D.; Hajnsek, I.; Pretzsch, H.; Papathanassiou, K.P. TanDEM-X Pol-InSAR performance for forest height estimation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar] [CrossRef]
- Lee, S.K.; Fatoyinbo, T.E. TanDEM-X Pol-InSAR inversion for mangrove canopy height estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3608–3618. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing with Imaging Radar; Signals and Communication Technology; Springer: Berlin/Heidelberg, Germany, 2009; p. 361. [Google Scholar] [CrossRef]
- Immitzer, M.; Neuwirth, M.; Böck, S.; Brenner, H.; Vuolo, F.; Atzberger, C. Optimal input features for tree species classification in Central Europe based on multi-temporal Sentinel-2 data. Remote Sens. 2019, 11, 2599. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, M.; McRoberts, R.E.; Tomppo, E.; Gschwantner, T.; Gabler, K. Comparisons of National Forest Inventories. In National Forest Inventories; Springer: Berlin/Heidelberg, Germany, 2010; pp. 19–32. [Google Scholar] [CrossRef]
- RIEGL. VQ-1560i Datasheet; RIEGL Laser Measurement Systems GmbH: Horn, Austria, 2019. [Google Scholar]
- Bauer-Marschallinger, B.; Sabel, D.; Wagner, W. Optimisation of global grids for high-resolution remote sensing data. Comput. Geosci. 2014, 72, 84–93. [Google Scholar] [CrossRef]
- Pfeifer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS–A framework for Airborne Laser Scanning data analysis. Comput. Environ. Urban Syst. 2014, 45, 125–136. [Google Scholar] [CrossRef]
- Hollaus, M.; Mandlburger, G.; Pfeifer, N.; Mücke, W. Land cover dependent derivation of digital surface models from airborne laser scanning data. In Proceedings of the ISPRS Commission III Symposium PCV 2010, IAPRS Volume XXXVIII Part 3A, Saint-Mandé, France, 1–3 September 2010; pp. 221–226. [Google Scholar]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating forest biomass to SAR data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Ranson, K.; Sun, G. Mapping biomass of a northern forest using multifrequency SAR data. IEEE Trans. Geosci. Remote Sens. 1994, 32, 388–396. [Google Scholar] [CrossRef]
- Vreugdenhil, M.; Wagner, W.; Bauer-Marschallinger, B.; Pfeil, I.; Teubner, I.; Rüdiger, C.; Strauss, P. Sensitivity of Sentinel-1 backscatter to vegetation dynamics: An Austrian case study. Remote Sens. 2018, 10, 1396. [Google Scholar] [CrossRef] [Green Version]
- Santoro, M.; Shvidenko, A.; McCallum, I.; Askne, J.; Schmullius, C. Properties of ERS-1/2 coherence in the Siberian boreal forest and implications for stem volume retrieval. Remote Sens. Environ. 2007, 106, 154–172. [Google Scholar] [CrossRef]
- Karila, K.; Vastaranta, M.; Karjalainen, M.; Kaasalainen, S. Tandem-X interferometry in the prediction of forest inventory attributes in managed boreal forests. Remote Sens. Environ. 2015, 159, 259–268. [Google Scholar] [CrossRef]
- Persson, H.J.; Fransson, J.E. Comparison between TanDEM-X-and ALS-based estimation of aboveground biomass and tree height in boreal forests. Scand. J. For. Res. 2017, 32, 306–319. [Google Scholar] [CrossRef] [Green Version]
- Dostálová, A.; Milenkovic, M.; Hollaus, M.; Wagner, W. Influence of Forest Structure on the Sentinel-1 Backscatter Variation-Analysis with Full-Waveform LiDAR Data. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Small, D.; Miranda, N.; Ewen, T.; Jonas, T. Reliably flattened radar backscatter for wet snow mapping from wide-swath sensors. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013. [Google Scholar]
- Atwood, D.K.; Small, D.; Gens, R. Improving PolSAR land cover classification with radiometric correction of the coherency matrix. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 848–856. [Google Scholar] [CrossRef]
- Small, D. Flattening gamma: Radiometric terrain correction for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Dostálová, A.; Hollaus, M.; Milenković, M.; Wagner, W. Forest area derivation from sentinel-1 data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 227. [Google Scholar] [CrossRef] [Green Version]
- ACube. Austrian Data Cube. An EODC Service for the Austrian Earth Observation User Community. Available online: https://acube.eodc.eu/ (accessed on 1 February 2021).
- Naeimi, V.; Elefante, S.; Cao, S.; Wagner, W.; Dostalova, A.; Bauer-Marschallinger, B. Geophysical parameters retrieval from Sentinel-1 SAR data: A case study for high performance computing at EODC. In Proceedings of the 24th High Performance Computing Symposium, Pasadena, CA, USA, 3–6 April 2016; pp. 1–8. [Google Scholar]
- SNAP. Sentinel Application Platform. Available online: https://step.esa.int/main/toolboxes/snap/ (accessed on 1 February 2021).
- Geoland. Digitales Geländemodell (DGM) Österreich. 2020. Available online: https://www.data.gv.at/katalog/dataset/dgm (accessed on 1 February 2021).
- Koskinen, J.T.; Pulliainen, J.T.; Hallikainen, M.T. The Use of ERS-1 SAR Data in Snow Melt Monitoring. IEEE Trans. Geosci. Remote Sens. 1997, 35, 601–610. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. R package version 3.3-13. 2020. Available online: https://CRAN.R-project.org/package=raste (accessed on 1 February 2021).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Latifi, H.; Koch, B. Evaluation of most similar neighbour and random forest methods for imputing forest inventory variables using data from target and auxiliary stands. Int. J. Remote Sens. 2012, 33, 6668–6694. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Lucas, R.M.; Cronin, N.; Lee, A.; Moghaddam, M.; Witte, C.; Tickle, P. Empirical relationships between AIRSAR backscatter and LiDAR-derived forest biomass, Queensland, Australia. Remote Sens. Environ. 2006, 100, 407–425. [Google Scholar] [CrossRef]
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the Northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Mermoz, S.; Le Toan, T.; Villard, L.; Réjou-Méchain, M.; Seifert-Granzin, J. Biomass assessment in the Cameroon savanna using ALOS PALSAR data. Remote Sens. Environ. 2014, 155, 109–119. [Google Scholar] [CrossRef]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and simulated GEDI lidar observations for forest structure mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Hagberg, J.O.; Ulander, L.M.; Askne, J. Repeat-pass SAR interferometry over forested terrain. IEEE Trans. Geosci. Remote Sens. 1995, 33, 331–340. [Google Scholar] [CrossRef]
- Askne, J.I.; Dammert, P.B.; Ulander, L.M.; Smith, G. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens. 1997, 35, 25–35. [Google Scholar] [CrossRef]
- Wegmüller, U.; Werner, C. Retrieval of vegetation parameters with SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1997, 35, 18–24. [Google Scholar] [CrossRef]
- Rüetschi, M.; Small, D.; Waser, L.T. Rapid Detection of Windthrows using Sentinel-1 C-band SAR Data. Remote Sens. 2019, 11, 115. [Google Scholar] [CrossRef] [Green Version]
- Lohberger, S.; Stängel, M.; Atwood, E.C.; Siegert, F. Spatial evaluation of Indonesia’s 2015 fire-affected area and estimated carbon emissions using Sentinel-1. Glob. Chang. Biol. 2018, 24, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Reiche, J.; Hamunyela, E.; Verbesselt, J.; Hoekman, D.; Herold, M. Improving near-real time deforestation monitoring in tropical dry forests by combining dense Sentinel-1 time series with Landsat and ALOS-2 PALSAR-2. Remote Sens. Environ. 2018, 204, 147–161. [Google Scholar] [CrossRef]
- Bouvet, A.; Mermoz, S.; Ballère, M.; Koleck, T.; Le Toan, T. Use of the SAR shadowing effect for deforestation detection with Sentinel-1 time series. Remote Sens. 2018, 10, 1250. [Google Scholar] [CrossRef] [Green Version]
- Way, J.; Paris, J.; Kasischke, E.; Slaughter, C.; Viereck, L.; Christensen, N.; Dobson, M.C.; Ulaby, F.; Richards, J.; Milne, A.; et al. The effect of changing environmental conditions on microwave signatures of forest ecosystems: Preliminary results of the March 1988 Alaskan aircraft SAR experiment. Int. J. Remote Sens. 1990, 11, 1119–1144. [Google Scholar] [CrossRef]
- Olesk, A.; Voormansik, K.; Põhjala, M.; Noorma, M. Forest change detection from Sentinel-1 and ALOS-2 satellite images. In Proceedings of the 2015 IEEE 5th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Singapore, 1–4 September 2015; pp. 522–527. [Google Scholar] [CrossRef]















| Product Name | Temporal Aggregation | Separate for Each Orbit | Number of Products |
|---|---|---|---|
| VV backscatter | FM, JJA, ON, year | yes | 8 |
| VH backscatter | FM, JJA, ON, year | yes | 8 |
| Cross ratio VH/VV | FM, JJA, ON, year | yes | 8 |
| Coherence | FM, JJA, ON, year | yes | 8 |
| Slope VV | year | no | 1 |
| Slope VH | year | no | 1 |
| Correlation VV | year | no | 1 |
| Correlation VH | year | no | 1 |
| Total number of products | 36 |
| Experiment | Fraction for Training | Removed Tiles |
|---|---|---|
| 1 | 75% | yes |
| 2 | 80% | yes |
| 3 | 75% | yes |
| 4 | 100% | no |
| Resolution | Number of Cells | |
|---|---|---|
| All | Forested | |
| 20 m | 264,103 | 234,819 |
| 40 m | 66,334 | 59,999 |
| 100 m | 10,771 | 10,071 |
| Bias | RMSE | Person’s R | |
|---|---|---|---|
| 20 m | −0.001 | 0.12 | 0.84 |
| 40 m | −0.001 | 0.10 | 0.89 |
| 100 m | 0.000 | 0.08 | 0.94 |
| Non-Stratified | 3 Classes | 4 Classes | |||||||
|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | H1 | H2 | H3 | H1 | H2 | H3 | |
| Bias | 4.3 | −0.7 | −6.1 | 3.9 | 0.2 | −3.8 | 3.6 | -0.4 | −4.7 |
| RMSE | 6.2 | 4.1 | 6.7 | 6.3 | 4.7 | 4.9 | 5.9 | 4.5 | 5.7 |
| Bias | 0.2 | 0.9 | 0.3 | ||||||
| RMSE | 5.1 | 5.2 | 5.1 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruggisser, M.; Dorigo, W.; Dostálová, A.; Hollaus, M.; Navacchi, C.; Schlaffer, S.; Pfeifer, N. Potential of Sentinel-1 C-Band Time Series to Derive Structural Parameters of Temperate Deciduous Forests. Remote Sens. 2021, 13, 798. https://doi.org/10.3390/rs13040798
Bruggisser M, Dorigo W, Dostálová A, Hollaus M, Navacchi C, Schlaffer S, Pfeifer N. Potential of Sentinel-1 C-Band Time Series to Derive Structural Parameters of Temperate Deciduous Forests. Remote Sensing. 2021; 13(4):798. https://doi.org/10.3390/rs13040798
Chicago/Turabian StyleBruggisser, Moritz, Wouter Dorigo, Alena Dostálová, Markus Hollaus, Claudio Navacchi, Stefan Schlaffer, and Norbert Pfeifer. 2021. "Potential of Sentinel-1 C-Band Time Series to Derive Structural Parameters of Temperate Deciduous Forests" Remote Sensing 13, no. 4: 798. https://doi.org/10.3390/rs13040798
APA StyleBruggisser, M., Dorigo, W., Dostálová, A., Hollaus, M., Navacchi, C., Schlaffer, S., & Pfeifer, N. (2021). Potential of Sentinel-1 C-Band Time Series to Derive Structural Parameters of Temperate Deciduous Forests. Remote Sensing, 13(4), 798. https://doi.org/10.3390/rs13040798