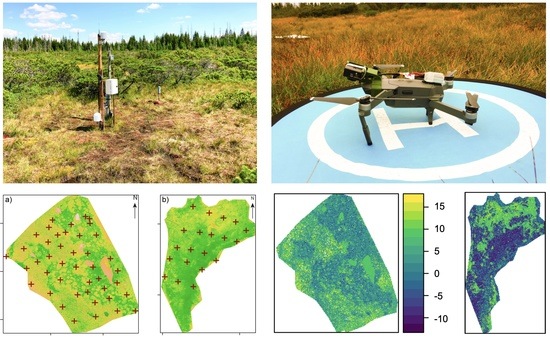
Mapping the Groundwater Level and Soil Moisture of a Montane Peat Bog Using UAV Monitoring and Machine Learning
Abstract
:1. Introduction
- Collect UAV RGB, multispectral, and thermal imagery along with ground truth data on GWL and SM over ten months;
- Extract a suite of variables (microtopographic drivers, vegetational, and temperature information) using a multi-sensor (RGB, multispectral, and thermal sensors) UAV monitoring approach;
- Spatiotemporally predict GWL and SM by the CAST ML model and assessing the importance of selected drivers; and
- Simulate prediction certainties across study areas, mimicking the environmental reality.
2. Materials and Methods
2.1. Site Description and Climate
2.2. Ground Survey
2.3. UAV Platforms and Cameras
2.4. Data Processing
2.4.1. RGB Scenes
2.4.2. Multispectral Scenes
2.4.3. Thermal Scenes
2.4.4. Input Variables
2.5. Model Description
3. Results
3.1. Predictive Outputs
3.2. AOA Calculations
4. Discussion
4.1. Model Performance
4.2. Interpretation of Model Predictions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grzybowski, M.; Glińska-Lewczuk, K. The Principal Threats to the Peatlands Habitats, in the Continental Bioregion of Central Europe—A Case Study of Peatland Conservation in Poland. J. Nat. Conserv. 2020, 53, 125778. [Google Scholar] [CrossRef]
- Keddy, P.A. Wetland Ecology: Principles and Conservation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-511-77817-9. [Google Scholar]
- Holden, J.; Wallage, Z.E.; Lane, S.N.; McDonald, A.T. Water Table Dynamics in Undisturbed, Drained and Restored Blanket Peat. J. Hydrol. 2011, 402, 103–114. [Google Scholar] [CrossRef]
- Spitzer, K.; Danks, H.V. Insect Biodiversity of Boreal Peat Bogs. Annu. Rev. Entomol. 2006, 51, 137–161. [Google Scholar] [CrossRef]
- Bates, P.D.; Neal, J.C.; Alsdorf, D.; Schumann, G.J.-P. Observing Global Surface Water Flood Dynamics. Surv. Geophys. 2014, 35, 839–852. [Google Scholar] [CrossRef]
- Kocum, J.; Oulehle, F.; Janský, B.; Bůzek, F.; Hruška, J.; Vlček, L. Geochemical Evidence for Peat Bog Contribution to the Streamflow Generation Process: Case Study of the Vltava River Headwaters, Czech Republic. Hydrol. Sci. J. 2016, 61, 2579–2589. [Google Scholar] [CrossRef] [Green Version]
- Schreiber, H. Moore des Böhmerwaldes und des Deutschen Südböhmen; 4. Band der Moorerhebungen des Deutsch-Österreichischen Moorvereins; Verlag des Deutschen Moorvereines in der Tchechoslowakei: Sebastiansberg, 1924. [Google Scholar]
- Bufková, I.; Stíbal, F.; Mikulášková, E. Restoration of Drained Mires in the Šumava National Park, Czech Republic. In Wetlands: Ecology, Conservation and Management, Restoration of Lakes, Streams, Floodplains, and Bogs in Europe; Eiseltová, M., Ed.; Springe: Dordrecht, The Netherlands, 2010; Volume 3, pp. 331–354. ISBN 978-90-481-9264-9. [Google Scholar]
- Bufková, I.; Prach, K. Linking Vegetation Pattern to Hydrology and Hydrochemistry in a Montane River Floodplain, the Šumava National Park, Central Europe. Wetl. Ecol. Manag. 2006, 14, 317–327. [Google Scholar] [CrossRef]
- Vlček, L.; Kocum, J.; Janský, B.; Šefrna, L.; Kučerová, A. Retention potential and hydrological balance of a peat bog: Case study of Rokytka Moors, Otava River headwaters, sw. Czechia. Geografie 2012, 117, 395–414. [Google Scholar] [CrossRef]
- Vlček, L.; Kocum, J.; Janský, B.; Šefrna, L.; Blažková, Š. Influence of Peat Soils on Runoff Process: Case Study of Vydra River Headwaters, Czechia. Geografie 2016, 121, 235–253. [Google Scholar] [CrossRef]
- Vlček, L.; Falátková, K.; Schneider, P. Identification of Runoff Formation with Two Dyes in a Mid-Latitude Mountain Headwater. Hydrol. Earth Syst. Sci. 2017, 21, 3025–3040. [Google Scholar] [CrossRef] [Green Version]
- Vlček, L.; Šípek, V.; Kofroňová, J.; Kocum, J.; Doležal, T.; Janský, B. Runoff Formation in a Catchment with Peat Bog and Podzol Hillslopes. J. Hydrol. 2020, 125633. [Google Scholar] [CrossRef]
- Doležal, T.; Vlček, L.; Kocum, J.; Janský, B. Evaluation of the Influence of Mountain Peat Bogs Restoration Measures on the Groundwater Level: Case Study Rokytka Peat Bog, the Šumava Mts., Czech Republic. AUC Geogr. 2017, 52, 141–150. [Google Scholar] [CrossRef] [Green Version]
- Doležal, T.; Vlček, L.; Kocum, J.; Janský, B. Hydrological Regime and Physico-Chemical Water Properties of Various Types of Peat Bog Sites: Case Study of Mezilesní Peat Bog, Šumava Mts. Geografie 2020, 125, 21–46. [Google Scholar] [CrossRef]
- Kubatova, A.; Prasil, K.; Vanova, M. Diversity of Soil Microscopic Fungi on Abandoned Industrial Deposits. Cryptogam. Mycol. Fr. 2002, 23, 205–219. [Google Scholar]
- Sipek, M.; Perčin, A.; Zgorelec, Ž.; Sajna, N. Morphological Plasticity and Ecophysiological Response of Ground Ivy (Glechoma Hederacea, Lamiaceae) in Contrasting Natural Habitats within Its Native Range. Plant Biosyst. Int. J. Deal. Asp. Plant Biol. 2021, 155, 136–147. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR System with Application to Forest Inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, J.; Nieberding, F.; Prinz, T.; Knoth, C. Analysis of Unmanned Aerial System-Based CIR Images in Forestry—A New Perspective to Monitor Pest Infestation Levels. Forests 2015, 6, 594–612. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.M.; McDermid, G.J.; Strack, M.; Lovitt, J. A New Method to Map Groundwater Table in Peatlands Using Unmanned Aerial Vehicles. Remote Sens. 2017, 9, 1057. [Google Scholar] [CrossRef] [Green Version]
- Lovitt, J.; Rahman, M.; McDermid, G. Assessing the Value of UAV Photogrammetry for Characterizing Terrain in Complex Peatlands. Remote Sens. 2017, 9, 715. [Google Scholar] [CrossRef] [Green Version]
- Lovitt, J.; Rahman, M.M.; Saraswati, S.; McDermid, G.J.; Strack, M.; Xu, B. UAV Remote Sensing Can Reveal the Effects of Low-Impact Seismic Lines on Surface Morphology, Hydrology, and Methane (CH4) Release in a Boreal Treed Bog. J. Geophys. Res. Biogeosciences 2018, 123, 1117–1129. [Google Scholar] [CrossRef] [Green Version]
- Harvey, M.C.; Hare, D.K.; Hackman, A.; Davenport, G.; Haynes, A.B.; Helton, A.; Lane, J.W.; Briggs, M.A. Evaluation of Stream and Wetland Restoration Using UAS-Based Thermal Infrared Mapping. Water 2019, 11, 1568. [Google Scholar] [CrossRef] [Green Version]
- Isokangas, E.; Davids, C.; Kujala, K.; Rauhala, A.; Ronkanen, A.-K.; Rossi, P.M. Combining Unmanned Aerial Vehicle-Based Remote Sensing and Stable Water Isotope Analysis to Monitor Treatment Peatlands of Mining Areas. Ecol. Eng. 2019, 133, 137–147. [Google Scholar] [CrossRef]
- Beyer, F.; Jurasinski, G.; Couwenberg, J.; Grenzdörffer, G. Multisensor Data to Derive Peatland Vegetation Communities Using a Fixed-Wing Unmanned Aerial Vehicle. Int. J. Remote Sens. 2019, 40, 9103–9125. [Google Scholar] [CrossRef]
- Kanevski, M.; Pozdnoukhov, A.; Pozdnukhov, A.; Timonin, V. Machine Learning for Spatial Environmental Data: Theory, Applications, and Software; EPFL Press: Lausanne, Switzerland, 2009; ISBN 0-8493-8237-8. [Google Scholar]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine Learning in Geosciences and Remote Sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; Walsh, M.G.; Sanderman, J.; Wheeler, I.; Harrison, S.P.; Prentice, I.C. Global Mapping of Potential Natural Vegetation: An Assessment of Machine Learning Algorithms for Estimating Land Potential. PeerJ 2018, 6, e5457. [Google Scholar] [CrossRef] [Green Version]
- Hengl, T.; MacMillan, R.A. Predictive Soil Mapping with R. 370; OpenGeoHub Foundation: Wageningen, The Netherlands, 2019. [Google Scholar]
- Gasch, C.K.; Hengl, T.; Gräler, B.; Meyer, H.; Magney, T.S.; Brown, D.J. Spatio-Temporal Interpolation of Soil Water, Temperature, and Electrical Conductivity in 3D + T: The Cook Agronomy Farm Data Set. Spat. Stat. 2015, 14, 70–90. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving Performance of Spatio-Temporal Machine Learning Models Using Forward Feature Selection and Target-Oriented Validation. Environ. Model. Softw. 2018, 101. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Predicting into Unknown Space? Estimating the Area of Applicability of Spatial Prediction Models. arXiv 2020, arXiv:2005.07939. Available online: https://arxiv.org/abs/2005.07939 (accessed on 5 July 2020).
- Rahaghi, A.I.; Lemmin, U.; Sage, D.; Barry, D.A. Achieving High-Resolution Thermal Imagery in Low-Contrast Lake Surface Waters by Aerial Remote Sensing and Image Registration. Remote Sens. Environ. 2019, 221, 773–783. [Google Scholar] [CrossRef]
- Perich, G.; Hund, A.; Anderegg, J.; Roth, L.; Boer, M.P.; Walter, A.; Liebisch, F.; Aasen, H. Assessment of Multi-Image Unmanned Aerial Vehicle Based High-Throughput Field Phenotyping of Canopy Temperature. Front. Plant Sci. 2020, 11, 150. [Google Scholar] [CrossRef]
- R: Unmanned Aerial Vehicle Remote Sensing Tools. Available online: http://finzi.psych.upenn.edu/library/uavRst/html/uavRst.html (accessed on 15 April 2018).
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. Discuss. 2015, 8, 2271–2312. [Google Scholar] [CrossRef] [Green Version]
- Minařík, R.; Langhammer, J.; Hanuš, J. Radiometric and Atmospheric Corrections of Multispectral ΜMCA Camera for UAV Spectroscopy. Remote Sens. 2019, 11, 2428. [Google Scholar] [CrossRef] [Green Version]
- Minařík, R.; Langhammer, J. Rapid Radiometric Calibration of Multiple Camera Array Using In-Situ Data For Uav Multispectral Photogrammetry. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W17, 209–215. [Google Scholar] [CrossRef] [Green Version]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D.C.; Merzlyak, M.N. Nondestructive Estimation of Anthocyanin Content in Grapevine Leaves. Am. J. Enol. Vitic. 2009, 60, 87–92. [Google Scholar]
- Visible Vegetation Index (VVI)—Planetary Habitability Laboratory @ UPR Arecibo. Available online: http://phl.upr.edu/projects/visible-vegetation-index-vvi (accessed on 13 February 2021).
- Hunt, E.R.; Doraiswamy, P.C.; McMurtrey, J.E.; Daughtry, C.S.T.; Perry, E.M.; Akhmedov, B. A Visible Band Index for Remote Sensing Leaf Chlorophyll Content at the Canopy Scale. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 103–112. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Lacaux, J.P.; Tourre, Y.M.; Vignolles, C.; Ndione, J.A.; Lafaye, M. Classification of Ponds from High-Spatial Resolution Remote Sensing: Application to Rift Valley Fever Epidemics in Senegal. Remote Sens. Environ. 2007, 106, 66–74. [Google Scholar] [CrossRef]
- Mathieu, R.; Pouget, M.; Cervelle, B.; Escadafal, R. Relationships between Satellite-Based Radiometric Indices Simulated Using Laboratory Reflectance Data and Typic Soil Color of an Arid Environment. Remote Sens. Environ. 1998, 66, 17–28. [Google Scholar] [CrossRef]
- Louhaichi, M.; Borman, M.M.; Young, W.C., III; Silberstein, T.B.; Mellbye, M.E.; Johnson, D.E. Evaluating Nitrogen Fertilization Rates on Grass Plant Growth Using Near-Earth and Ground-Level Photography. Available online: _ https://www.researchgate.net/profile/Mounir-Louhaichi/publication/252424580_EVALUATING_NITROGEN_FERTILIZATION_RATES_ON_GRASS_PLANT_GROWTH_USING_NEAR-EARTH_AND_GROUND-LEVEL_PHOTOGRAPHY/links/53ee2a890cf23733e80b3264/EVALUATING-NITROGEN-FERTILIZATION-RATES-ON-GRASS-PLANT-GROWTH-USING-NEAR-EARTH-AND-GROUND-LEVEL-PHOTOGRAPHY.pdf (accessed on 6 September 2019).
- Zevenbergen, L.W.; Thorne, C.R. Quantitative Analysis of Land Surface Topography. Earth Surf. Process. Landf. 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that Quantifies Topographic Heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA Spatial Modeling of Plant Species Distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Kuenzer, C.; Zhang, J.; Jing, L.; Huadong, G.; Dech, S. Thermal infrared remote sensing of surface and underground coal fires. In Thermal Infrared Remote Sensing; Springer: New York, NY, USA, 2013; pp. 429–451. [Google Scholar] [CrossRef]
- Yang, Y.; Lee, X. Four-Band Thermal Mosaicking: A New Method to Process Infrared Thermal Imagery of Urban Landscapes from UAV Flights. Remote Sens. 2019, 11, 1365. [Google Scholar] [CrossRef] [Green Version]
- Acorsi, M.G.; Gimenez, L.M.; Martello, M. Assessing the Performance of a Low-Cost Thermal Camera in Proximal and Aerial Conditions. Remote Sens. 2020, 12, 3591. [Google Scholar] [CrossRef]
- Usman, U.; Yelwa, S.A.; Gulumbe, S.U.; Danbaba, A. Modelling Relationship between NDVI and Climatic Variables Using Geographically Weighted Regression. J. Math. Sci. Appl. 2013, 1, 24–28. [Google Scholar]
- Loranty, M.; Davydov, S.; Kropp, H.; Alexander, H.; Mack, M.; Natali, S.; Zimov, N. Vegetation Indices Do Not Capture Forest Cover Variation in Upland Siberian Larch Forests. Remote Sens. 2018, 10, 1686. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M. The Caret Package. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 15 April 2020).
- Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping Daily Air Temperature for Antarctica Based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef] [Green Version]
- Lindsey, C.; Sheather, S. Variable Selection in Linear Regression. Stata J. 2010, 10, 650–669. [Google Scholar] [CrossRef]
- Kuhn, M. Caret: Classification and Regression Training. The Comprehensive R Archive Network. 2019. Available online: https://topepo.github.io/caret/ (accessed on 15 April 2020).
- Meyer, H.; Reudenbach, C.; Wöllauer, S.; Nauss, T. Importance of Spatial Predictor Variable Selection in Machine Learning Applications—Moving from Data Reproduction to Spatial Prediction. Ecol. Model. 2019, 411, 108815. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M. 15 Variable Importance|The Caret Package. Available online: https://topepo.github.io/caret/variable-importance.html (accessed on 3 May 2020).
- Valois, R.; Schaffer, N.; Figueroa, R.; Maldonado, A.; Yáñez, E.; Hevia, A.; Yánez Carrizo, G.; MacDonell, S. Characterizing the Water Storage Capacity and Hydrological Role of Mountain Peatlands in the Arid Andes of North-Central Chile. Water 2020, 12, 1071. [Google Scholar] [CrossRef] [Green Version]
- Roberts, E.M.; Mienis, F.; Rapp, H.T.; Hanz, U.; Meyer, H.K.; Davies, A.J. Oceanographic Setting and Short-Timescale Environmental Variability at an Arctic Seamount Sponge Ground. Deep Sea Res. Part Oceanogr. Res. Pap. 2018, 138, 98–113. [Google Scholar] [CrossRef]
- Pohjankukka, J.; Pahikkala, T.; Nevalainen, P.; Heikkonen, J. Estimating the Prediction Performance of Spatial Models via Spatial K-Fold Cross Validation. Int. J. Geogr. Inf. Sci. 2017, 31, 2001–2019. [Google Scholar] [CrossRef]
- Brenning, A. Spatial Cross-Validation and Bootstrap for the Assessment of Prediction Rules in Remote Sensing: The R Package Sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: New York, NY, USA, 2012; pp. 5372–5375. Available online: https://ieeexplore.ieee.org/abstract/document/6352393?casa_token=WQv5L9Qp2QoAAAAA:Jl1ZwwC5TqRkE4-iWltdIm04VnOP0vECD3BFS-kUhIAev0TMEVdZ-HGK4cGz_A0cQikhGiA (accessed on 29 June 2019).
- Petermann, E.; Meyer, H.; Nussbaum, M.; Bossew, P. Mapping the Geogenic Radon Potential for Germany by Machine Learning. Sci. Total Environ. 2021, 754, 142291. [Google Scholar] [CrossRef] [PubMed]
- Rezanezhad, F.; Price, J.S.; Quinton, W.L.; Lennartz, B.; Milojevic, T.; van Cappellen, P. Structure of Peat Soils and Implications for Water Storage, Flow and Solute Transport: A Review Update for Geochemists. Chem. Geol. 2016, 429, 75–84. [Google Scholar] [CrossRef]
- Hayward, P.M.; Clymo, R.S. Profiles of Water Content and Pore Size in Sphagnum and Peat, and Their Relation to Peat Bog Ecology. Proc. R. Soc. Lond. B Biol. Sci. 1982, 215, 299–325. [Google Scholar]
- Campbell, D.I.; Williamson, J.L. Evaporation from a Raised Peat Bog. J. Hydrol. 1997, 193, 142–160. [Google Scholar] [CrossRef]
- Price, J.S.; Schlotzhauer, S.M. Importance of Shrinkage and Compression in Determining Water Storage Changes in Peat: The Case of a Mined Peatland. Hydrol. Process. 1999, 13, 2591–2601. [Google Scholar] [CrossRef] [Green Version]
- Moore, P.A.; Lukenbach, M.C.; Kettridge, N.; Petrone, R.M.; Devito, K.J.; Waddington, J.M. Peatland Water Repellency: Importance of Soil Water Content, Moss Species, and Burn Severity. J. Hydrol. 2017, 554, 656–665. [Google Scholar] [CrossRef] [Green Version]
- Lozano-Parra, J.; Pulido, M.; Lozano-Fondón, C.; Schnabel, S. How Do Soil Moisture and Vegetation Covers Influence Soil Temperature in Drylands of Mediterranean Regions? Water 2018, 10, 1747. [Google Scholar] [CrossRef] [Green Version]
- Abu-Hamdeh, N.H. Thermal Properties of Soils as Affected by Density and Water Content. Biosyst. Eng. 2003, 86, 97–102. [Google Scholar] [CrossRef]
- Luikov, A.V. The Drying of Peat. Ind. Eng. Chem. 1935, 27, 406–409. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A Comparison of Methods for Determining Forest Evapotranspiration and Its Components: Sap-Flow, Soil Water Budget, Eddy Covariance and Catchment Water Balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Peli, E.R.; Nagy, J.G.; Cserhalmi, D. In Situ Measurements of Seasonal Productivity Dynamics in Two Sphagnum Dominated Mires in Hungary. Carpathian J. Earth Environ. Sci. 2015, 10, 231–240. [Google Scholar]
- D′ Acunha, B.; Morillas, L.; Black, T.A.; Christen, A.; Johnson, M.S. Net Ecosystem Carbon Balance of a Peat Bog Undergoing Restoration: Integrating CO2 and CH4 Fluxes from Eddy Covariance and Aquatic Evasion with DOC Drainage Fluxes. J. Geophys. Res. Biogeosciences 2019, 124, 884–901. [Google Scholar] [CrossRef] [Green Version]
- Šimanauskienė, R.; Linkevičienė, R.; Bartold, M.; Dąbrowska-Zielińska, K.; Slavinskienė, G.; Veteikis, D.; Taminskas, J. Peatland Degradation: The Relationship between Raised Bog Hydrology and Normalized Difference Vegetation Index. Ecohydrology 2019, 12. [Google Scholar] [CrossRef]
- Price, J. Soil Moisture, Water Tension, and Water Table Relationships in a Managed Cutover Bog. J. Hydrol. 1997, 202, 21–32. [Google Scholar] [CrossRef]
- Grabs, T.; Seibert, J.; Bishop, K.; Laudon, H. Modeling Spatial Patterns of Saturated Areas: A Comparison of the Topographic Wetness Index and a Dynamic Distributed Model. J. Hydrol. 2009, 373, 15–23. [Google Scholar] [CrossRef] [Green Version]
- Rinderer, M.; van Meerveld, H.J.; Seibert, J. Topographic Controls on Shallow Groundwater Levels in a Steep, Prealpine Catchment: When Are the TWI Assumptions Valid? Water Resour. Res. 2014, 50, 6067–6080. [Google Scholar] [CrossRef]
- Harris, A.; Baird, A.J. Microtopographic Drivers of Vegetation Patterning in Blanket Peatlands Recovering from Erosion. Ecosystems 2019, 22, 1035–1054. [Google Scholar] [CrossRef] [Green Version]
- Leempoel, K.; Parisod, C.; Geiser, C.; Daprà, L.; Vittoz, P.; Joost, S. Very High-resolution Digital Elevation Models: Are Multi-scale Derived Variables Ecologically Relevant? Methods Ecol. Evol. 2015, 6, 1373–1383. [Google Scholar] [CrossRef]
- Sappington, J.M.; Longshore, K.M.; Thompson, D.B. Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert. J. Wildl. Manag. 2007, 71, 1419–1426. [Google Scholar] [CrossRef]












| Predictor Variables | Definition | Formula |
|---|---|---|
| RGB spectral indices (orthoimages) | ||
| RGI | Red-green ratio index [40] | (red/green) |
| VVI | Visible vegetation index [41] | (1 − (red − 30)/(red + 30)) * (1 − (green − 50)/(green + 50)) * (1 − (blue − 1)/(blue + 1)) |
| VDVI | Visible-band Difference Vegetation Index | (2 * green − red − blue)/(2 * green + red + blue) |
| VARI | Visible Atmospherically Resistant Index | (green-red)/(green + red-blue) |
| TGI | Triangular Greenness Index [42] | −0.5[190(red670 − red550) − 120(red670 − red480)] |
| SI | Spectral Slope Saturation Index | (red-blue)/(red + blue) |
| SHP | Shape index | 2 * (red − green − blue)/(green − blue) |
| SCI | Soil Colour Index | (red-green)/(red + green) |
| SAT | Overall Saturation Index | max(red, green, blue) − min(red, green, blue))/max(red, green, blue) |
| NGRDI | Normalized Green Red Difference Index [43] | (green-red)/(green + (red)) |
| NDTI | Normalized Difference Turbidity Index Water [44] | (red-green)/(red + green) |
| NDI | Normalized Difference Index | (red-green)/(red + green) |
| HI | Primary Colours Hue Index [45] | (2 * red-green-blue)/(green-blue) |
| GRVI | Green-Red Vegetation Index | (green-red)/(green + red) |
| GLI | Green Leaf Index [46] | (2 * green − red − blue)/(2*green + red + blue) |
| GLAI | Green Leaf Area Index | (25 * (green − red)/(green + red − blue) + 1.25) |
| ExG | Excess Green | 2 * green-red-blue/red + green + blue |
| ERGBVE | Enhanced Red-Green-Blue Vegetation Index | 3.14159 * ((green2-(red * blue))/(green2+(red * blue))) |
| CI | Coloration Index | (red − blue)/red |
| BI | Brightness Index | sqrt((red2 + green2 + blue*2)/3 |
| RI | Redness Index | red2/(blue*green3) |
| HUE | Hue Overall Index | atan(2 * (red − green − blue)/30.5 * (green − blue)) |
| Vegetation index (Multispectral scenes) | ||
| NDVI | Normalized Difference Vegetation Index [43] | (NIR-red/NIR + red) |
| Topomorphometric indices (DSMs) | ||
| Slope | Steepest Slope Angle [°] | |
| ProfCurv | Profile Curvature [°] | Direction of the steepest slope. Affects the acceleration or deceleration of water [47]. |
| PlnCurv | Plan Curvature [°] | Horizontal curvature intersecting with the x–y surface plane. Affects the convergence or divergence of water [47]. |
| WEI | Wind Exposition Index | Values below 1 indicate wind-shaded areas, whereas values above 1 indicate areas exposed to the wind. |
| TRI (1, 4)* | Terrain Ruggedness Index (1)* [m] | A measure of terrain complexity/heterogeneity. It calculates the sum change in elevation between a grid cell and its neighboring grid cells. The moving window radius determines how many cells are used to calculate the elevation change [48]. Value is always ≥ 0 m, where 0 represents the minimum roughness. |
| VRM (1, 4)* | Vector Ruggedness Measure | A measure of terrain complexity/variance that captures variability in slope and aspect in a single measure. Ruggedness is measured as the dispersion of vectors orthogonal to the surface within a specific neighborhood. The radius of the moving window determines how many cells are used to calculate the change in ruggedness. |
| TPI | Topographic Position Index | Difference between the elevation of the cell and the mean of the elevation in surrounding cells [49]. Value is positive when the point is higher than its surroundings, zero when in a flat area or mid-slope, and negative when lower than its surroundings. |
| TWI | SAGA Wetness Index [37] | Describes the tendency of an area to accumulate water. |
| Thermal information (Thermal scenes) | ||
| Temperature | Relative Surface Temperature [°C] | |
| Ground truth observation variables | ||
| GWL | Groundwater Level [cm] | Describes the source of soil water as well precipitation in peatland ecosystems. |
| SM | Gravimetric Water Content | Controls soil respiration that is defined as a sum of organic matter decomposition and root respiration. |
| Date | Location | Variables | mtry | RMSE | R2 | MAE | RMSE_SD | R2_SD | MAE_SD | MEAN (ref.) | MEDIAN (ref.) | SD (ref.) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| August 2018 | UP | GWL | 2 | 22.15 | 0.33 | 14.84 | 9.95 | 0.22 | 5.05 | 32.20 | 41.00 | 27.10 |
| September 2018 | UP | GWL | 2 | 8.66 | 0.33 | 7.11 | 1.62 | 0.21 | 1.34 | 18.40 | 18.70 | 10.10 |
| October 2018 | UP | GWL | 2 | 10.32 | 0.13 | 7.65 | 3.50 | 0.15 | 2.36 | 22.70 | 22.40 | 10.80 |
| November 2018 | UP | GWL | 2 | 7.52 | 0.18 | 5.79 | 1.07 | 0.18 | 0.92 | 8.99 | 8.70 | 7.82 |
| May 2019 | UP | GWL | 2 | 6.64 | 0.42 | 5.21 | 1.44 | 0.21 | 1.18 | 4.86 | 3.50 | 8.05 |
| June 2019 | UP | GWL | 2 | 1.96 | 0.32 | 1.59 | 0.67 | 0.12 | 0.55 | 4.50 | 4.84 | 2.31 |
| July 2019 | UP | GWL | 2 | 7.57 | 0.23 | 6.41 | 1.71 | 0.24 | 1.16 | 24.70 | 22.60 | 8.74 |
| August 2019 | UP | GWL | 3 | 7.65 | 0.43 | 5.72 | 1.85 | 0.20 | 1.44 | 4.16 | 4.00 | 9.64 |
| September 2019 | UP | GWL | 2 | 9.92 | 0.41 | 7.32 | 4.00 | 0.24 | 1.66 | 3.19 | 4.60 | 12.70 |
| November 2019 | UP | GWL | 2 | 6.05 | 0.36 | 4.97 | 0.79 | 0.33 | 0.54 | 5.51 | 6.00 | 7.27 |
| Average score (MEANGWL_UP) | 8.84 | 0.31 | 6.66 | 2.66 | 0.21 | 1.62 | 12.92 | 13.63 | 10.45 | |||
| August 2018 | LP | GWL | 2 | 6.46 | 0.78 | 5.69 | 5.79 | 0.16 | 5.01 | 22.00 | 19.10 | 12.20 |
| September 2018 | LP | GWL | 2 | 5.36 | 0.46 | 4.79 | 3.92 | 0.45 | 3.61 | 0.31 | −0.80 | 5.65 |
| October 2018 | LP | GWL | 2 | 5.44 | 0.46 | 4.12 | 2.05 | 0.44 | 1.45 | 14.40 | 14.70 | 5.83 |
| November 2018 | LP | GWL | 2 | 4.32 | 0.56 | 3.62 | 2.16 | 0.29 | 1.70 | 0.52 | −1.15 | 5.28 |
| May 2019 | LP | GWL | 2 | 4.09 | 0.34 | 2.96 | 1.51 | 0.35 | 0.72 | -3.35 | −4.95 | 4.58 |
| June 2019 | LP | GWL | 2 | 6.03 | 0.47 | 4.71 | 2.24 | 0.49 | 1.40 | 9.32 | 9.20 | 6.85 |
| July 2019 | LP | GWL | 2 | 8.10 | 0.30 | 5.69 | 4.20 | 0.32 | 2.39 | 15.80 | 14.80 | 8.23 |
| August 2019 | LP | GWL | 2 | 4.05 | 0.73 | 3.40 | 3.21 | 0.26 | 2.41 | -0.91 | −3.05 | 6.02 |
| September 2019 | LP | GWL | 2 | 4.46 | 0.53 | 3.68 | 1.91 | 0.39 | 1.80 | 0.31 | −0.80 | 5.65 |
| November 2019 | LP | GWL | 2 | 5.89 | 0.13 | 4.58 | 1.24 | 0.14 | 1.15 | 0.52 | −1.15 | 5.28 |
| Average score (MEANGWL_LP) | 5.42 | 0.48 | 4.32 | 2.82 | 0.33 | 2.16 | 5.89 | 4.59 | 6.56 | |||
| August 2018 | UP | SM | 2 | 2.60 | 0.12 | 2.09 | 0.46 | 0.10 | 0.27 | 6.27 | 6.18 | 27.10 |
| September 2018 | UP | SM | 2 | 3.24 | 0.28 | 2.71 | 0.58 | 0.22 | 0.29 | 7.10 | 6.67 | 10.10 |
| June 2019 | UP | SM | 2 | 2.83 | 0.12 | 2.34 | 0.91 | 0.12 | 0.56 | 3.61 | 3.09 | 2.31 |
| July 2019 | UP | SM | 2 | 1.73 | 0.29 | 1.48 | 0.53 | 0.22 | 0.39 | 3.99 | 4.18 | 8.74 |
| August 2018 | UP | SM | 2 | 2.85 | 0.41 | 2.30 | 0.61 | 0.38 | 0.48 | 6.17 | 6.09 | 9.64 |
| September 2018 | UP | SM | 2 | 2.82 | 0.22 | 2.31 | 0.42 | 0.17 | 0.39 | 6.92 | 7.06 | 12.70 |
| November 2018 | UP | SM | 2 | 3.35 | 0.33 | 2.56 | 0.91 | 0.17 | 0.80 | 7.38 | 7.61 | 7.27 |
| Average score (MEANSM_UP) | 2.77 | 0.25 | 2.26 | 0.63 | 0.20 | 0.45 | 5.92 | 5.84 | 11.12 | |||
| August 2018 | LP | SM | 2 | 2.42 | 0.48 | 2.06 | 0.72 | 0.37 | 0.67 | 11.60 | 12.30 | 12.20 |
| September 2018 | LP | SM | 2 | 3.96 | 0.45 | 3.56 | 2.01 | 0.42 | 1.92 | 15.60 | 16.10 | 5.65 |
| June 2019 | LP | SM | 2 | 3.33 | 0.52 | 2.71 | 1.77 | 0.32 | 1.43 | 7.79 | 9.52 | 6.85 |
| July 2019 | LP | SM | 2 | 2.77 | 0.55 | 2.37 | 0.94 | 0.30 | 0.60 | 7.69 | 8.20 | 8.23 |
| August 2018 | LP | SM | 2 | 5.83 | 0.21 | 4.77 | 1.17 | 0.26 | 0.82 | 11.70 | 12.60 | 6.02 |
| September 2018 | LP | SM | 2 | 2.59 | 0.59 | 1.99 | 0.96 | 0.41 | 0.48 | 11.90 | 11.50 | 5.65 |
| November 2018 | LP | SM | 2 | 5.32 | 0.47 | 4.30 | 1.95 | 0.17 | 1.93 | 13.80 | 14.50 | 5.28 |
| Average score (MEANSM_LP) | 3.75 | 0.47 | 3.11 | 1.36 | 0.32 | 1.12 | 11.44 | 12.10 | 7.13 | |||
| Average score (MEANall) | 5.54 | 0.38 | 4.34 | 2.02 | 0.27 | 1.44 | 9.11 | 9.05 | 8.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lendzioch, T.; Langhammer, J.; Vlček, L.; Minařík, R. Mapping the Groundwater Level and Soil Moisture of a Montane Peat Bog Using UAV Monitoring and Machine Learning. Remote Sens. 2021, 13, 907. https://doi.org/10.3390/rs13050907
Lendzioch T, Langhammer J, Vlček L, Minařík R. Mapping the Groundwater Level and Soil Moisture of a Montane Peat Bog Using UAV Monitoring and Machine Learning. Remote Sensing. 2021; 13(5):907. https://doi.org/10.3390/rs13050907
Chicago/Turabian StyleLendzioch, Theodora, Jakub Langhammer, Lukáš Vlček, and Robert Minařík. 2021. "Mapping the Groundwater Level and Soil Moisture of a Montane Peat Bog Using UAV Monitoring and Machine Learning" Remote Sensing 13, no. 5: 907. https://doi.org/10.3390/rs13050907
APA StyleLendzioch, T., Langhammer, J., Vlček, L., & Minařík, R. (2021). Mapping the Groundwater Level and Soil Moisture of a Montane Peat Bog Using UAV Monitoring and Machine Learning. Remote Sensing, 13(5), 907. https://doi.org/10.3390/rs13050907