Sea Level Fusion of Satellite Altimetry and Tide Gauge Data by Deep Learning in the Mediterranean Sea
Abstract
:1. Introduction
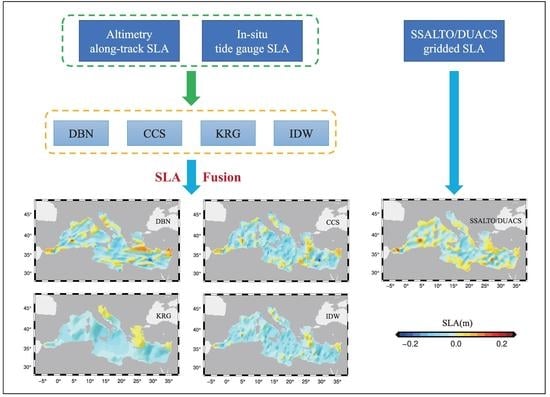
2. Materials and Methods
2.1. Satellite-Altimetry-Derived SLA Datasets
2.2. Tide Gauge Data and VLM Corrections
2.3. SLA Estimation Model Based on DBN Method
3. Results
3.1. Step One: Training Without Tide Gauge Data
3.2. Step Two: Training with Virtual Tide Gauges
3.3. Step Three: Training with In-Situ Tide Gauges
4. Discussion
4.1. The Capability of Describing the Spatial Characteristics
4.2. Other Potential Deep Learning Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Kirezci, E.; Young, I.R.; Ranasinghe, R.; Muis, S.; Nicholls, R.J.; Lincke, D.; Hinkel, J. Projections of global-scale extreme sea levels and resulting episodic coastal flooding over the 21st Century. Sci. Rep. 2020, 10, 11629. [Google Scholar] [CrossRef] [PubMed]
- Bonaduce, A.; Pinardi, N.; Oddo, P.; Spada, G.; Larnicol, G. Sea-level variability in the Mediterranean Sea from altimetry and tide gauges. Clim. Dyn. 2016, 47, 2851–2866. [Google Scholar] [CrossRef] [Green Version]
- Nerem, R.S.; Mitchum, G.T. Estimates of vertical crustal motion derived from differences of TOPEX/POSEIDON and tide gauge sea level measurements. Geophys. Res. Lett. 2002, 29, 40–44. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Shum, C.K.; Braun, A.; Miteovica, J.X. Vertical crustal motion determined by satellite altimetry and tide gauge data in Fennoscandia. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Schöne, T.; Schön, N.; Thaller, D. IGS Tide Gauge Benchmark Monitoring Pilot Project (TIGA): Scientific benefits. J. Geod. 2009, 83, 249–261. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X. Application of the Multi-Adaptive Regression Splines to Integrate Sea Level Data from Altimetry and Tide Gauges for Monitoring Extreme Sea Level Events. Mar. Geod. 2015, 38, 261–276. [Google Scholar] [CrossRef]
- Avsar, N.B.; Jin, S.; Kutoglu, H.; Gurbuz, G. Sea level change along the Black Sea coast from satellite altimetry, tide gauge and GPS observations. Geod. Geodyn. 2016, 7, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Taibi, H.; Haddad, M. Estimating trends of the Mediterranean Sea level changes from tide gauge and satellite altimetry data (1993–2015). J. Oceanol. Limnol. 2019, 37, 1176–1185. [Google Scholar] [CrossRef]
- Grgić, M.; Nerem, R.S.; Bašić, T. Absolute Sea Level Surface Modeling for the Mediterranean from Satellite Altimeter and Tide Gauge Measurements. Mar. Geod. 2017, 40, 239–258. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Aldrich, C. Flotation froth image recognition with convolutional neural networks. Miner. Eng. 2019, 132, 183–190. [Google Scholar] [CrossRef]
- Liu, N.; Xu, Y.; Tian, Y.; Ma, H.; Wen, S. Background classification method based on deep learning for intelligent automotive radar target detection. Future Gener. Comput. Syst. 2019, 94, 524–535. [Google Scholar] [CrossRef]
- Du, Y.; Song, W.; He, Q.; Huang, D.; Liotta, A.; Su, C. Deep learning with multi-scale feature fusion in remote sensing for automatic oceanic eddy detection. Inf. Fusion 2019, 49, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Ducournau, A.; Fablet, R. Deep learning for ocean remote sensing: An application of convolutional neural networks for super-resolution on satellite-derived SST data. In Proceedings of the 2016 9th IAPR Workshop on Pattern Recogniton in Remote Sensing (PRRS), Cancun, Mexico, 4 December 2016; pp. 1–6. [Google Scholar]
- Braakmann-Folgmann, A.; Roscher, R.; Wenzel, S.; Uebbing, B.; Kusche, J. Sea Level Anomaly Prediction using Recurrent Neural Networks. arXiv 2017, arXiv:1710.07099. [Google Scholar]
- Bruneau, N.; Polton, J.; Williams, J.; Holt, J. Estimation of global coastal sea level extremes using neural networks. Environ. Res. Lett. 2020, 15, 074030. [Google Scholar] [CrossRef]
- Zhu, S.-B.; Li, Z.-L.; Zhang, S.-M.; Ying, Y.; Zhang, H.-F. Deep belief network-based internal valve leakage rate prediction approach. Measurement 2019, 133, 182–192. [Google Scholar] [CrossRef]
- Wang, H.Z.; Wang, G.B.; Li, G.Q.; Peng, J.C.; Liu, Y.T. Deep belief network based deterministic and probabilistic wind speed forecasting approach. Appl. Energy 2016, 182, 80–93. [Google Scholar] [CrossRef]
- Huang, H.B.; Li, R.X.; Yang, M.L.; Lim, T.C.; Ding, W.P. Evaluation of vehicle interior sound quality using a continuous restricted Boltzmann machine-based DBN. Mech. Syst. Signal Process. 2017, 84, 245–267. [Google Scholar] [CrossRef] [Green Version]
- Ji, H.; Tian, L.; Li, J.; Tong, R.; Guo, Y.; Zeng, Q. Spatial-spectral Fusion of HY-1C COCTS/CZI Data for Coastal Water Remote Sensing Using Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating Ground-Level PM2.5 by Fusing Satellite and Station Observations: A Geo-Intelligent Deep Learning Approach. Geophys. Res. Lett. 2017, 44, 11, 985–911, 993. [Google Scholar] [CrossRef] [Green Version]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Smith, W.; Wessel, P. Gridding with continuous curvature splines in tension. Geophysics 1990, 55, 293–305. [Google Scholar] [CrossRef]
- Ducet, N.; Le Traon, P.Y.; Reverdin, G. Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and -2. J. Geophys. Res. Ocean. 2000, 105, 19477–19498. [Google Scholar] [CrossRef]
- AVISO. SSALTO/DUACS User Handbook: (M) SLA and (M) ADT Near-Real Time and Delayed Time Products; CNES: Ile-de-France, France, 2014. [Google Scholar]
- Scharroo, R.; Leuliette, E.; Lillibridge, J.; Byrne, D.; Naeije, M.; Mitchum, G. RADS: Consistent multi-mission products. In Proceedings of the 20 Years of Progress in Radar Altimatry, Venice, Italy, 24–29 September 2012. [Google Scholar]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New Data Systems and Products at the Permanent Service for Mean Sea Level. J. Coast. Res. 2012, 29, 493–504. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Wöppelmann, G. Long-term vertical land motion from double-differenced tide gauge and satellite altimetry data. J. Geod. 2014, 88, 207–222. [Google Scholar] [CrossRef]
- Bruyninx, C.; Habrich, H.; Söhne, W.; Kenyeres, A.; Stangl, G.; Völksen, C. Enhancement of the EUREF permanent network services and products. In Geodesy for planet Earth; Springer: Berlin/Heidelberg, Germany, 2012; pp. 27–34. [Google Scholar]
- Carrère, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing-comparisons with observations. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef] [Green Version]
- Wöppelmann, G.; Marcos, M. Coastal sea level rise in southern Europe and the nonclimate contribution of vertical land motion. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Li, T.; Yuan, Q.; Zhang, L. Estimating Regional Ground-Level PM2. 5 Directly From Satellite Top-Of-Atmosphere Reflectance Using Deep Belief Networks. J. Geophys. Res. Atmos. 2018, 123, 13, 875–813, 886. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Mohamed, A.-R.; Dahl, G.E.; Hinton, G. Acoustic modeling using deep belief networks. IEEE Trans. Audio Speech Lang. Process. 2011, 20, 14–22. [Google Scholar] [CrossRef]
- Chen, Z.; Li, W. Multisensor Feature Fusion for Bearing Fault Diagnosis Using Sparse Autoencoder and Deep Belief Network. IEEE Trans. Instrum. Meas. 2017, 66, 1693–1702. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Smolensky, P. Information Processing in Dynamical Systems: Foundations of Harmony Theory; Colorado University at Boulder Department of Computer Science: Boulder, CO, USA, 1986. [Google Scholar]
- Hinton. A Practical Guide to Training Restricted Boltzmann Machines. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 599–619. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Lea, C.; Flynn, M.D.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks for Action Segmentation and Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 156–165. [Google Scholar]
- Sun, Q.; Wan, J.; Liu, S. Estimation of sea level variability in the China Sea and its vicinity using the SARIMA and LSTM models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3317–3326. [Google Scholar] [CrossRef]
- Fan, S.; Xiao, N.; Dong, S. A novel model to predict significant wave height based on long short-term memory network. Ocean Eng. 2020, 205, 107298. [Google Scholar] [CrossRef]
- Liu, H.; He, B.; Qin, P.; Zhang, X.; Guo, S.; Mu, X. Sea level anomaly intelligent inversion model based on LSTM-RBF network. Meteorol. Atmos. Phys. 2020, 1–15. [Google Scholar] [CrossRef]
- Hewage, P.; Behera, A.; Trovati, M.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Mu, L.; Wang, L.; Ranjan, R.; Zomaya, A.Y. Temporal convolutional networks for the advance prediction of ENSO. Sci. Rep. 2020, 10, 1–15. [Google Scholar] [CrossRef]







| Tide Gauge Number | DBN | CCS | KRG | IDW | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CORR | STD | RMSE | CORR | STD | RMSE | CORR | STD | RMSE | CORR | STD | RMSE | |
| 3 | 0.877 | 0.040 | 0.040 | 0.914 | 0.036 | 0.044 | 0.862 | 0.043 | 0.053 | 0.820 | 0.048 | 0.059 |
| 6 | 0.796 | 0.038 | 0.038 | 0.652 | 0.046 | 0.064 | 0.781 | 0.038 | 0.052 | 0.785 | 0.037 | 0.052 |
| 7 | 0.872 | 0.041 | 0.041 | 0.846 | 0.045 | 0.056 | 0.843 | 0.045 | 0.057 | 0.810 | 0.049 | 0.061 |
| 8 | 0.939 | 0.024 | 0.025 | 0.775 | 0.043 | 0.056 | 0.811 | 0.040 | 0.053 | 0.800 | 0.041 | 0.054 |
| 10 | 0.790 | 0.039 | 0.039 | 0.643 | 0.047 | 0.065 | 0.759 | 0.040 | 0.053 | 0.769 | 0.039 | 0.053 |
| 11 | 0.904 | 0.034 | 0.034 | 0.895 | 0.037 | 0.048 | 0.879 | 0.039 | 0.052 | 0.832 | 0.044 | 0.057 |
| 12 | 0.893 | 0.032 | 0.034 | 0.866 | 0.035 | 0.049 | 0.857 | 0.036 | 0.049 | 0.861 | 0.035 | 0.050 |
| 13 | 0.943 | 0.023 | 0.025 | 0.775 | 0.043 | 0.057 | 0.824 | 0.039 | 0.052 | 0.823 | 0.039 | 0.052 |
| 17 | 0.859 | 0.038 | 0.040 | 0.838 | 0.041 | 0.055 | 0.842 | 0.041 | 0.054 | 0.847 | 0.040 | 0.053 |
| 18 | 0.933 | 0.025 | 0.028 | 0.833 | 0.035 | 0.049 | 0.825 | 0.036 | 0.049 | 0.833 | 0.035 | 0.048 |
| 19 | 0.922 | 0.029 | 0.031 | 0.855 | 0.040 | 0.050 | 0.865 | 0.039 | 0.049 | 0.848 | 0.041 | 0.051 |
| 20 | 0.901 | 0.037 | 0.037 | 0.852 | 0.045 | 0.060 | 0.862 | 0.044 | 0.058 | 0.846 | 0.047 | 0.060 |
| 21 | 0.886 | 0.050 | 0.051 | 0.846 | 0.057 | 0.064 | 0.833 | 0.059 | 0.068 | 0.798 | 0.064 | 0.073 |
| 24 | 0.864 | 0.038 | 0.039 | 0.765 | 0.047 | 0.055 | 0.772 | 0.046 | 0.057 | 0.769 | 0.046 | 0.057 |
| Mean | 0.884 | 0.035 | 0.036 | 0.811 | 0.043 | 0.055 | 0.830 | 0.042 | 0.054 | 0.817 | 0.043 | 0.056 |
| Tide Gauge Number | DBN | CCS | KRG | IDW | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CORR | STD | RMSE | CORR | STD | RMSE | CORR | STD | RMSE | CORR | STD | RMSE | |
| 3 | 0.869 | 0.041 | 0.041 | 0.859 | 0.034 | 0.034 | 0.866 | 0.042 | 0.043 | 0.813 | 0.049 | 0.050 |
| 6 | 0.883 | 0.029 | 0.029 | 0.737 | 0.036 | 0.056 | 0.836 | 0.033 | 0.034 | 0.812 | 0.036 | 0.037 |
| 7 | 0.860 | 0.043 | 0.043 | 0.844 | 0.042 | 0.044 | 0.853 | 0.044 | 0.046 | 0.855 | 0.044 | 0.046 |
| 8 | 0.929 | 0.025 | 0.026 | 0.802 | 0.041 | 0.048 | 0.794 | 0.041 | 0.045 | 0.797 | 0.041 | 0.044 |
| 10 | 0.908 | 0.026 | 0.026 | 0.835 | 0.040 | 0.041 | 0.865 | 0.031 | 0.032 | 0.833 | 0.034 | 0.035 |
| 11 | 0.892 | 0.036 | 0.036 | 0.872 | 0.039 | 0.040 | 0.846 | 0.042 | 0.044 | 0.804 | 0.047 | 0.048 |
| 12 | 0.881 | 0.033 | 0.034 | 0.826 | 0.039 | 0.042 | 0.859 | 0.035 | 0.038 | 0.862 | 0.035 | 0.038 |
| 13 | 0.933 | 0.025 | 0.025 | 0.865 | 0.034 | 0.041 | 0.811 | 0.040 | 0.044 | 0.816 | 0.039 | 0.043 |
| 17 | 0.857 | 0.038 | 0.039 | 0.835 | 0.041 | 0.044 | 0.853 | 0.039 | 0.042 | 0.858 | 0.039 | 0.042 |
| 18 | 0.916 | 0.027 | 0.029 | 0.843 | 0.035 | 0.038 | 0.846 | 0.035 | 0.036 | 0.839 | 0.035 | 0.037 |
| 19 | 0.907 | 0.032 | 0.034 | 0.909 | 0.030 | 0.031 | 0.896 | 0.034 | 0.034 | 0.875 | 0.036 | 0.037 |
| 20 | 0.886 | 0.040 | 0.040 | 0.755 | 0.055 | 0.061 | 0.814 | 0.050 | 0.053 | 0.800 | 0.051 | 0.054 |
| 21 | 0.868 | 0.054 | 0.054 | 0.829 | 0.054 | 0.054 | 0.848 | 0.057 | 0.059 | 0.788 | 0.065 | 0.067 |
| 24 | 0.870 | 0.036 | 0.037 | 0.791 | 0.046 | 0.048 | 0.793 | 0.044 | 0.049 | 0.790 | 0.045 | 0.050 |
| Mean | 0.890 | 0.035 | 0.035 | 0.829 | 0.040 | 0.044 | 0.841 | 0.040 | 0.043 | 0.824 | 0.043 | 0.045 |
| Scheme | TG Stations Used as Training Data | Spatial Distribution Characteristics |
|---|---|---|
| b | [ 1,2,4,5,9,14,15,16,22,23] | Evenly distributed |
| c | [ 2,3,4,6,8,14,17,20,21,24] | Evenly distributed |
| d | [ 2,11,12,14,16,17,18,19,20,22] | Inside |
| e | [ 1,3,5,6,7,8,9,10,13,15,21] | Upper left corner |
| f | [ 4,12,14,17,18,19,22,23,24] | Bottom right corner |
| g | [ ] | No tide gauge is selected |
| Scheme | DBN | CCS | KRG | IDW | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CORR | STD | RMSE | CORR | STD | RMSE | CORR | STD | RMSE | CORR | STD | RMSE | |
| b | 0.890 | 0.035 | 0.035 | 0.829 | 0.040 | 0.044 | 0.841 | 0.040 | 0.043 | 0.824 | 0.043 | 0.045 |
| c | 0.907 | 0.031 | 0.032 | 0.859 | 0.034 | 0.036 | 0.853 | 0.038 | 0.040 | 0.844 | 0.039 | 0.041 |
| d | 0.863 | 0.039 | 0.040 | 0.776 | 0.052 | 0.057 | 0.793 | 0.047 | 0.050 | 0.786 | 0.047 | 0.050 |
| e | 0.885 | 0.036 | 0.037 | 0.817 | 0.047 | 0.050 | 0.820 | 0.044 | 0.047 | 0.821 | 0.044 | 0.047 |
| f | 0.846 | 0.042 | 0.042 | 0.765 | 0.056 | 0.062 | 0.763 | 0.050 | 0.052 | 0.758 | 0.050 | 0.052 |
| g | 0.861 | 0.039 | 0.040 | 0.761 | 0.052 | 0.057 | 0.786 | 0.047 | 0.050 | 0.785 | 0.047 | 0.050 |
| Mean | 0.875 | 0.037 | 0.038 | 0.801 | 0.047 | 0.051 | 0.809 | 0.044 | 0.047 | 0.803 | 0.045 | 0.047 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Jin, T.; Gao, X.; Wen, H.; Schöne, T.; Xiao, M.; Huang, H. Sea Level Fusion of Satellite Altimetry and Tide Gauge Data by Deep Learning in the Mediterranean Sea. Remote Sens. 2021, 13, 908. https://doi.org/10.3390/rs13050908
Yang L, Jin T, Gao X, Wen H, Schöne T, Xiao M, Huang H. Sea Level Fusion of Satellite Altimetry and Tide Gauge Data by Deep Learning in the Mediterranean Sea. Remote Sensing. 2021; 13(5):908. https://doi.org/10.3390/rs13050908
Chicago/Turabian StyleYang, Lianjun, Taoyong Jin, Xianwen Gao, Hanjiang Wen, Tilo Schöne, Mingyu Xiao, and Hailan Huang. 2021. "Sea Level Fusion of Satellite Altimetry and Tide Gauge Data by Deep Learning in the Mediterranean Sea" Remote Sensing 13, no. 5: 908. https://doi.org/10.3390/rs13050908
APA StyleYang, L., Jin, T., Gao, X., Wen, H., Schöne, T., Xiao, M., & Huang, H. (2021). Sea Level Fusion of Satellite Altimetry and Tide Gauge Data by Deep Learning in the Mediterranean Sea. Remote Sensing, 13(5), 908. https://doi.org/10.3390/rs13050908