Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies
Abstract
:1. Introduction
2. Past VIIRS Recalibration Efforts
3. Current Recalibration Methodology, Algorithms, and Improvements
3.1. Improvements in Absolute Radiometric Accuracy
3.2. Improvements in Long-Term Radiometric Stability
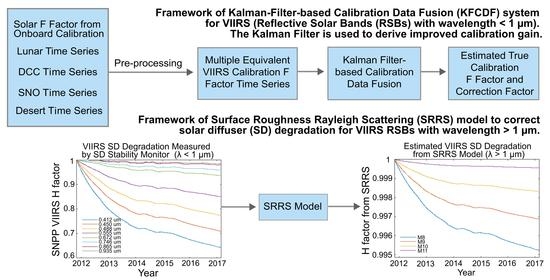
3.3. A Comprehensive Approach for Improved Accuracy and Long-Term Stability: The Kalman Filter Approach
3.3.1. The Five Calibration Methods for Stability Monitoring and Calibration Preprocessing
- (a)
- Solar diffuser-F factor
- (b) Lunar-F factor
- (c) Deep Convective Cloud (DCC) Data
- (d) SNOx with MODIS over Sonoran Desert
- (e) Vicarious monitoring over Libyan desert
3.3.2. Normalization of the F Factor
3.3.3. Kalman Filter-Based VIIRS Calibration Data Fusion
3.4. The Surface Roughness Rayleigh Scattering Model (SRRS) for Improving Calibration Stability (Bands with Wavelength > 1 µm)
3.5. Algorithm Improvements for the Thermal Emissive Bands
3.6. Recalibration Improvements for the DNB
3.7. Geolocation Recalibration Improvements
4. Verification and Validation of Recalibrated Data
4.1. Evaluation of Version 2 Recalibrated S-NPP VIIR RSB SDR over DCCs
4.2. F-Factor Comparison with other Independent Calibrations
4.2.1. Comparisons between OC and V1 SD F-Factors
4.2.2. Comparison between V1, OC and V2 F-Factors
4.2.3. Comparisons between NASA F-Factors and NOAA V2 F-Factors
4.3. Evaluation of Version 2 Reprocessed S-NPP VIIR TEB SDRs
4.4. Evaluation of Version 2 Reprocessed S-NPP VIIRS Geolocation Products
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Recalibration Processing System with High-Performance Computing
A.1. Super Computer System and Software for the Reprocessing
A.2. Calibration Parameter Input Datasets/Lookup Tables, Raw Data, and Data Volume Reduction
A.3. Multiple Versions of RDR Consideration
A.4. Data Format
A.5. Data Distribution



A.6. OnDemand Reprocessing
- The VIIRS SDR team could regenerate the dataset from scratch using the raw data record requested by the user, and provide the data to the user through the network. When this is done, the reprocessed SDR data can be removed from the server so they do not take up space;
- Alternatively, the VIIRS SDR team can obtain an account on the user’s computer, install the processing software ADL, and the input files as well as the raw data records. Then, the VIIRS SDR data can be produced on the user’s computer.
Appendix B. Look Up Table Updates in the Operational Datasets
| 23 February 2012 | VIIRS-SDR-GEO-DNB-PARAM-LUT; VIIRS-SDR-GEO-IMG-PARAM-LUT; VIIRS-SDR-GEO-MOD-PARAM-LUT; |
| 29 February 2012 | VIIRS-SDR-DELTA-C-LUT; VIIRS-SDR-GAIN-LUT; |
| 07 March 2012 | VIIRS-SDR-BB-TEMP-COEFFS-LUT; VIIRS-SDR-DELTA-C-LUT; VIIRS-SDR-GAIN-LUT; |
| VIIRS-SDR-RADIOMETRIC-PARAM-LUT; VIIRS-SDR-TELE-COEFFS-LUT; | |
| 15 March 2012 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 29 March 2012 | VIIRS-SDR-GEO-DNB-PARAM-LUT; |
| 24 April 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 25 April 2012 | VIIRS-SDR-RADIOMETRIC-PARAM-LUT; |
| 11 May 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 24 May 2012 | VIIRS-SDR-RSR-LUT; |
| 08 June 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 09 July 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 03 August 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 09 August 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; VIIRS-SDR-QA-LUT; VIIRS-SDR-RSR-LUT; |
| 10 August 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 17 August 2012 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 06 September 2012 | VIIRS-SDR-RSR-LUT; |
| 27 September 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 31 October 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 29 November 2012 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 11 December 2012 | VIIRS-SDR-GEO-DNB-PARAM-LUT; VIIRS-SDR-GEO-IMG-PARAM-LUT; VIIRS-SDR-GEO-MOD-PARAM-LUT; |
| 20 December 2012 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 24 January 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 14 February 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; VIIRS-SDR-GEO-DNB-PARAM-LUT; |
| 21 February 2013 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 21 March 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 28 March 2013 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 05 April 2013 | VIIRS-SDR-RSR-LUT; |
| 18 April 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; VIIRS-SDR-GEO-DNB-PARAM-LUT; VIIRS-SDR-GEO-IMG-PARAM-LUT; VIIRS-SDR-GEO-MOD-PARAM-LUT; |
| VIIRS-SDR-GEO-MOD-PARAM-LUT; | |
| 16 May 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 20 June 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 10 July 2013 | VIIRS-SDR-RADIOMETRIC-PARAM-LUT; |
| 18 July 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 08 August 2013 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 19 August 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 23 August 2013 | VIIRS-SDR-GEO-DNB-PARAM-LUT; VIIRS-SDR-GEO-IMG-PARAM-LUT; VIIRS-SDR-GEO-MOD-PARAM-LUT; |
| 19 September 2013 | VIIRS-SDR-DNB-C-COEFFS-LUT; |
| 14 November 2013 | VIIRS-RSBAUTOCAL-VOLT-LUT; VIIRS-SDR-CAL-AUTOMATE-LUT; VIIRS-SDR-RADIOMETRIC-PARAM-V2-LUT; VIIRS-SDR-RELATIVE-SPECTRAL-RESPONSE-LUT; |
| VIIRS-SDR-RELATIVE-SPECTRAL-RESPONSE-LUT; | |
| 18 March 2014 | VIIRS-SDR-RADIOMETRIC-PARAM-V3-LUT; |
| 10 April 2014 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 01 May 2014 | VIIRS-SDR-DELTA-C-LUT; |
| 22 May 2014 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 25 September 2014 | VIIRS-SDR-DG-ANOMALY-DN-LIMITS-LUT; |
| 01 October 2014 | VIIRS-SDR-RELATIVE-SPECTRAL-RESPONSE-LUT; |
| 06 March 2015 | VIIRS-SDR-DELTA-C-LUT; |
| 22 June 2015 | VIIRS-SDR-EBBT-LUT; |
| 30 November 2015 | VIIRS-SDR-CAL-AUTOMATE-LUT; |
| 05 January 2017 | DNB-DN0 |
| 08 March 2017 | CMNGEO-PARAM-LUT; VIIRS-RSBAUTOCAL-VOLT-LUT; VIIRS-SDR-BB-TEMP-COEFFS-LUT; |
| VIIRS-SDR-CAL-AUTOMATE-LUT; VIIRS-SDR-COEFF-A-LUT; VIIRS-SDR-COEFF-B-LUT; | |
| VIIRS-SDR-DELTA-C-LUT; VIIRS-SDR-DNB-FRAME-TO-ZONE-LUT; VIIRS-SDR-DNB-RVF-LUT; | |
| VIIRS-SDR-EBBT-LUT; VIIRS-SDR-EMISSIVE-LUT; VIIRS-SDR-GAIN-LUT; | |
| VIIRS-SDR-HAM-ER-LUT; VIIRS-SDR-OBC-ER-LUT; VIIRS-SDR-OBC-RR-LUT; | |
| VIIRS-SDR-OBS-TO-PIXELS-LUT; VIIRS-SDR-QA-LUT; VIIRS-SDR-RADIOMETRIC-PARAM-V3-LUT; | |
| VIIRS-SDR-REFLECTIVE-LUT; VIIRS-SDR-RELATIVE-SPECTRAL-RESPONSE-LUT; VIIRS-SDR-RTA-ER-LUT; | |
| VIIRS-SDR-RVF-LUT; VIIRS-SDR-SOLAR-IRAD-LUT; VIIRS-SDR-TELE-COEFFS-LUT; |
References
- Zhou, L.; Divakarla, M.; Liu, X.; Layns, A.; Goldberg, M. An Overview of the Science Performances and Calibration/Validation of Joint Polar Satellite System Operational Products. Remote Sens. 2019, 11, 698. [Google Scholar] [CrossRef] [Green Version]
- Barrie, J.D.; Fuqua, P.D.; Meshishnek, M.J.; Ciofalo, M.R.; Chu, C.T.; Chaney, J.A.; Moision, R.M.; Graziani, L. Root cause determination of on-orbit degradation of the VIIRS rotating telescope assembly. In Proceedings of the Volume 8510, Earth Observing Systems XVII, San Diego, CA, USA, 15 October 2012; p. 85101. [Google Scholar] [CrossRef] [Green Version]
- Rausch, K.; Houchin, S.; Cardema, J.; Moy, G.; Haas, E.; De Luccia, F. Automated calibration of the Suomi National Polar-Orbiting Partnership (S-NPP) Visible Infrared Imaging Radiometer Suite (VIIRS) reflective solar bands. J. Geophys. Res. 2013, 118, 13–434. [Google Scholar] [CrossRef]
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS Sensor Data Record Verification, Validation, and Long-Term Performance Monitoring. J. Geophys. Res. Atmos. 2013, 118, 11664–11678. [Google Scholar] [CrossRef]
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The Solar Spectral Irradiance from 200 to 2400 nm as Measured by the SOLSPEC Spectrometer from the ATLAS and EURECA Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar] [CrossRef]
- Xiong, X.; Angal, A.; Barnes, W.L.; Chen, H.; Chiang, V.; Geng, X.; Li, Y.; Twedt, K.; Wang, Z.; Wilson, T.; et al. Updates of Moderate Resolution Imaging Spectroradiometer on-orbit calibration uncertainty assessments. J. Appl. Remote Sens. 2018, 12, 034001. [Google Scholar] [CrossRef]
- JPSS GS Systems Engineering. Joint Polar Satellite System (JPSS) Ground Segment Data Product Specification (GSegDPS); Goddard Space Flight Center Greenbelt: Maryland, MD, USA, 2019.
- JPSS. Joint Polar Satellite System (JPSS) VIIRS Performance Requirements Document; Revision, H., Ed.; NASA GSFC: Maryland, MD, USA, 2017.
- JPSS. Joint Polar Satellite System (JPSS) National Environmental Satellite, Data, and Information Service (NESDIS) Environmental Satellite Processing Center (ESPC) Requirements Document (JERD) Volume 1; NASA GSFC: Maryland, MD, USA, 2018.
- Ohring, G.; Wielicki, B.; Spencer, R.; Emery, B.; Datla, R. Satellite Instrument Calibration for Measuring Global Climate Change. Bull. Am. Meteor. Soc. 2005, 86, 1303–1314. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Young, D.F.; Mlynczak, M.G.; Thome, K.J.; Leroy, S.; Corliss, J.; Anderson, J.G.; Ao, C.O.; Bantges, R.; Best, F.; et al. Achieving climate change absolute accuracy in orbit. Bull. Am. Meteorol. Soc. 2013, 94, 1519–1539. [Google Scholar] [CrossRef] [Green Version]
- Fox, N.; Aiken, J.; Barnett, J.J.; Briottet, X.; Carvell, R.; Frohlich, C.; Groom, S.B.; Hagolle, O.; Haigh, J.D.; Kieffer, H.H.; et al. Traceable radiometry underpinning terrestrial-and helio-studies (TRUTHS). Adv. Space Res. 2003, 32, 2253–2261. [Google Scholar] [CrossRef]
- Fox, N.; Green, P. Traceable Radiometry Underpinning Terrestrial-and Helio-Studies (TRUTHS): An Element of a Space-Based Climate and Calibration Observatory. Remote Sens. 2020, 12, 2400. [Google Scholar] [CrossRef]
- Zou, C.Z.; Zhou, L.; Lin, L.; Sun, N.; Chen, Y.; Flynn, L.E.; Zhang, B.; Cao, C.; Iturbide-Sanchez, F.; Beck, T.; et al. The Reprocessed Suomi NPP Satellite Observations. Remote Sens. 2020, 12, 2891. [Google Scholar] [CrossRef]
- Blonski, S.; Cao, C. Suomi NPP VIIRS Reflective Solar Bands Operational Calibration Reprocessing. Remote Sens. 2015, 7, 16131–16149. [Google Scholar] [CrossRef] [Green Version]
- Uprety, S.; Cao, C.; Xiong, X.; Wang, W.; Zhang, B.; Taeyoung, C.; Blonski, S.; Shao, X. Improving S-NPP VIIRS Reflective Solar Band (RSB) Calibration Accuracy through Reprocessing. GSICS Q. 2018, 12. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C.; Bai, Y.; Blonski, S.; Schull, M.A. Assessment of the NOAA S-NPP VIIRS Geolocation Reprocessing Improvements. Remote Sens. 2017, 9, 974. [Google Scholar] [CrossRef] [Green Version]
- Choi, T.; Shao, X.; Cao, C. On-orbit radiometric calibration of Suomi NPP VIIRS reflective solar bands using the Moon and solar diffuser. Appl. Opt. 2018, 57, 9533–9542. [Google Scholar] [CrossRef]
- Cao, C.; Wang, W.; Blonski, S.; Zhang, B. Radiometric traceability diagnosis and bias correction for the Suomi NPP VIIRS long-wave infrared channels during blackbody unsteady states. J. Geophys. Res. Atmos. 2017, 122, 5285–5297. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C.; Ignatov, A.; Liang, X.; Li, Z.; Wang, L.; Zhang, B.; Blonski, S.; Li, J. Improving the Calibration of Suomi NPP VIIRS Thermal Emissive Bands During Blackbody Warm-Up/Cool-Down. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1977–1994. [Google Scholar] [CrossRef]
- Lin, G.G.; Wolfe, R.E.; Dellomo, J.J.; Tan, B.; Zhang, P. SNPP and NOAA-20 VIIRS on-orbit geolocation trending and improvements. Earth Obs. Syst. XXV 2020, 11501, 1150112. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. Radiometric calibration of the Visible Infrared Imaging Radiometer Suite reflective solar bands with robust characterizations and hybrid calibration coefficients. Appl. Opt. 2015, 54, 9331–9342. [Google Scholar] [CrossRef]
- Choi, T.; Shao, X.; Cao, C.; Weng, F. Radiometric Stability Monitoring of the Suomi NPP Visible Infrared Imaging Radiometer Suite (VIIRS) Reflective Solar Bands Using the Moon. Remote Sens. 2016, 8, 15. [Google Scholar] [CrossRef] [Green Version]
- Lei, N.; Xiong, X. Estimation of the accuracy of the SNPP VIIRS SD BRDF degradation factor determined by the solar diffuser stability monitor. In Proceedings of the Earth Observing Systems XX, San Diego, CA, USA, 8 September 2015; Volume 9607. [Google Scholar]
- Sun, J.; Wang, M. On-orbit calibration of Visible Infrared Imaging Radiometer Suite reflective solar bands and its challenges using a solar diffuser. Appl. Opt. 2015, 54, 7210–7223. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Wang, M. VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products. Remote Sens. 2016, 8, 194. [Google Scholar] [CrossRef] [Green Version]
- Choi, T.; Cao, C. S-NPP VIIRS on-orbit calibration coefficient improvements with yaw maneuver reanalysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7460–7465. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X. Impacts of the Angular Dependence of the Solar Diffuser BRDF Degradation Factor on the SNPP VIIRS Reflective Solar Band On-Orbit Radiometric Calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1537–1543. [Google Scholar] [CrossRef]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Wang, Z.; Wu, A. Assessment of S-NPP VIIRS On-Orbit Radiometric Calibration and Performance. Remote Sens. 2016, 8, 84. [Google Scholar] [CrossRef] [Green Version]
- Baker, N.; Kilcoyne, H. Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document (ATBD); Goddard Space Flight Center: Greenbelt, MA, USA, 2013.
- Choi, T.; Sun, J.; Zhang, B.; Wang, Z.; Cao, C.; Weng, F.; Wang, M. Suomi-NPP VIIRS Initial Reprocessing Improvements and Validations in the Reflective Solar Bands. In Proceedings of the Earth Observing Systems XXII, San Diego, CA, USA, 5 September 2017. [Google Scholar]
- Ardanuy, P.E.; Puschell, J.J.; Moyer, D.; Vandermierden, N.; Rausch, K.; De Luccia, F. VIIRS reflective solar bands on-orbit calibration coefficient performance using imagery and moderate band intercomparisons. In Proceedings of the Remote Sensing System Engineering V, San Diego, CA, USA, 23 September 2014. [Google Scholar]
- Xiong, X.; Shimoda, H.; Fulbright, J.; Anderson, S.; Lei, N.; Efremova, B.; Wang, Z.; McIntire, J.; Chiang, K.; Xiong, X. The solar vector error within the SNPP Common GEO code, the correction, and the effects on the VIIRS SDR RSB calibration. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization III, Beijing, China, 19 November 2014. [Google Scholar]
- Uprety, S.; Cao, C. Suomi NPP VIIRS Reflective Solar Band On-Orbit Radiometric Stability and Accuracy Assessment Using Desert and Antarctica Dome C Sites. Remote Sens. Environ. 2015, 166, 106–115. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C.; Xiong, X.; Blonski, S.; Wu, A.; Shao, X. Radiometric Intercomparison between Suomi-NPP VIIRS and Aqua MODIS Reflective Solar Bands Using Simultaneous Nadir Overpass in the Low Latitudes. J. Atmos. Ocean. Technol. 2013, 30, 2720–2736. [Google Scholar] [CrossRef]
- Sayer, A.M.; Hsu, N.C.; Bettenhausen, C.; Holz, R.E.; Lee, J.; Quinn, G.; Veglio, P. Cross-calibration of S-NPP VIIRS moderate-resolution reflective solar bands against MODIS Aqua over dark water scenes. Atmos. Meas. Tech. 2017, 10, 1425–1444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Houtekamer, P.L.; Zhang, F. Review of the Ensemble Kalman Filter for Atmospheric Data Assimilation. Mon. Weather Rev. 2016, 144, 4489–4532. [Google Scholar] [CrossRef]
- Gao, J.B.; Harris, C.J. Some remarks on Kalman filters for the multisensor fusion. Inf. Fusion 2002, 3, 191–201. [Google Scholar] [CrossRef]
- Caron, F.; Duflos, E.; Pomorski, D.; Vanheeghe, F. GPS/IMU data fusion using multisensor Kalman filtering: Introduction of contextual aspects. Inf. Fusion 2006, 7, 221–230. [Google Scholar] [CrossRef]
- Loffeld, O.; Nies, H.; Knedlik, S.; Yu, W. Phase Unwrapping for SAR Interferometry—A Data Fusion Approach by Kalman Filtering. IEEE Trans. Geosci. Remote Sens. 2008, 46, 47–58. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. Visible Infrared Imaging Radiometer Suite solar diffuser calibration and its challenges using a solar diffuser stability monitor. Appl. Opt. 2014, 53, 8571–8584. [Google Scholar] [CrossRef]
- Shao, X.; Cao, C.; Liu, T.-C. Spectral Dependent Degradation of the Solar Diffuser on Suomi-NPP VIIRS Due to Surface Roughness-Induced Rayleigh Scattering. Remote Sens. 2016, 8, 254. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Liu, T.; Xiong, X.; Cao, C.; Choi, T.; Angal, A. Surface Roughness-Induced Spectral Degradation of Multi-Spaceborne Solar Diffusers Due to Space Radiation Exposure. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8658–8671. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C. DCC radiometric sensitivity to spatial resolution, cluster size, and LWIR calibration bias based on VIIRS observations. J. Atmos. Ocean. Technol. 2015, 32, 48–60. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C. Monitoring the NOAA operational VIIRS RSB and DNB calibration stability using monthly and semi-monthly deep convective clouds time series. Remote Sens. 2016, 8, 32. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Wielicki, B.A.; Yang, P.; Stackhouse, P.W.; Lin, B.; Young, D.F. Application of deep convective cloud albedo observation to satellite-based study of the terrestrial atmosphere: Monitoring the stability of spaceborne measurements and assessing absorption anomaly. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2594–2599. [Google Scholar]
- Wang, W.; Cao, C. Evaluation of NOAA-20 VIIRS Reflective Solar Bands Early On-Orbit Performance Using Daily Deep Convective Clouds Recent Improvements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3975–3985. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting Simultaneous Nadir Overpasses among Polar-Orbiting Meteorological Satellites for the Intersatellite Calibration of Radiometers. J. Atmos. Ocean. Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Grossman, E.; Gouzman, I. Space environment effects on polymers in low earth orbit. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater 2003, 208, 48–57. [Google Scholar] [CrossRef]
- Shao, X.; Liu, T.-C.; Xiong, X.; Cao, C.; Choi, T.; Angal, A. Modeling spectral degradation of MODIS and VIIRS solar diffusers. In Proceedings of the Earth Observing Systems XXIV, San Diego, CA, USA, 9 September 2019. [Google Scholar]
- Lei, N.; Xiong, X. Suomi NPP VIIRS Solar Diffuser BRDF Degradation Factor at Short-Wave Infrared Band Wavelengths. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6212–6216. [Google Scholar] [CrossRef]
- Ignatov, A.; Petrenko, B.; Kihai, Y.; Stroup, J.; Dash, P.; Liang, X.; Gladkova, I.; Zhou, X.; Sapper, J.; Xu, F. JPSS SST Products at NOAA. Am. Geophys. Union 2016, 2016, OD14B–2407. [Google Scholar]
- Uprety, S.; Cao, C.; Gu, Y.; Shao, X.; Blonski, S.; Zhang, B. Calibration improvements in S-NPP VIIRS DNB sensor data record using version 2 reprocessing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9602–9611. [Google Scholar] [CrossRef]
- Geis, J.; Florio, C.; Moyer, D.; Rausch, K.; De Luccia, F. VIIRS Day-Night Band gain and offset determination and performance. In Proceedings of the Earth Observing Systems XVII, San Diego, CA, USA, 15 October 2012; Volume 8510. [Google Scholar]
- De Miguel, A.S.; Kyba, C.C.; Zamorano, J.; Gallego, J.; Gaston, K.J. The nature of the diffuse light near cities detected in nighttime satellite imagery. Sci. Rep. 2020, 10, 1–16. [Google Scholar]
- Coesfeld, J.; Kuester, T.; Kuechly, H.U.; Kyba, C. Reducing Variability and Removing Natural Light from Nighttime Satellite Imagery: A Case Study Using the VIIRS DNB. Sensors 2020, 20, 3287. [Google Scholar] [CrossRef]
- Cao, C.; Bai, Y. Quantitative analysis of VIIRS DNB nightlight point source for light power estimation and stability monitoring. Remote Sens. 2014, 6, 11915–11935. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; McIntire, J.; Oudrari, H.; Schwarting, T.; Xiong, X. A new method for SUOMI-NPP VIIRS day–night band on-orbit radiometric calibration. IEEE Trans. Geosci. Remote Sens. 2015, 53, 324–334. [Google Scholar]
- Butler, J.J.; Xiong, X.; Barnes, R.A.; Patt, F.S.; Sun, J.; Chiang, K. An overview of Suomi NPP VIIRS calibration maneuvers. In Proceedings of the Earth Observing Systems XVII, San Diego, CA, USA, 15 October 2012; Volume 8510. [Google Scholar]
- Mills, S.; Weiss, S.; Liang, C. VIIRS day/night band (DNB) stray light characterization and correction. In Proceedings of the Earth Observing Systems XVIII, San Diego, CA, USA, 23 September 2013; Volume 8866. [Google Scholar]
- Shao, X.; Liu, T.-C.; Uprety, S.; Wang, W.; Zhang, B.; Cao, C. A light contamination ranking index-based method for automating VIIRS day/night band stray light correction. In Proceedings of the Earth Observing Systems XXIII, San Diego, CA, USA, 7 September 2018; Volume 10764. [Google Scholar]
- Wilson, T.; Xiong, X. Intercomparison of the SNPP and NOAA-20 VIIRS DNB high-gain stage using observations of bright stars. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8038–8045. [Google Scholar] [CrossRef]
- Wilson, T.; Xiong, X. Performance assessments of the SNPP and N20 VIIRS DNB using observations of bright stars. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIV, Online Only. 20 September 2020; Volume 11530. [Google Scholar]
- Cao, C.; Bai, Y.; Wang, W.; Choi, T. Radiometric Inter-Consistency of VIIRS DNB on Suomi NPP and NOAA-20 from Observations of Reflected Lunar Lights over Deep Convective Clouds. Remote Sens. 2019, 11, 934. [Google Scholar] [CrossRef] [Green Version]
- Ryan, R.E.; Pagnutti, M.; Burch, K.; Leigh, L.; Ruggles, T.; Cao, C.; Aaron, D.; Blonski, S.; Helder, D. The Terra Vega Active Light Source: A First Step in a New Approach to Perform Nighttime Absolute Radiometric Calibrations and Early Results Calibrating the VIIRS DNB. Remote Sens. 2019, 11, 710. [Google Scholar] [CrossRef] [Green Version]
- Doelling, D.R.; Wu, A.; Xiong, X.; Scarino, B.R.; Bhatt, R.; Haney, C.O.; Gopalan, A. The radiometric stability and scaling of collection 6 Terra-and Aqua-MODIS VIS, NIR, and SWIR spectral bands. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4520–4535. [Google Scholar] [CrossRef]
- Doelling, D.R.; Hong, G.; Morstad, D.; Bhatt, R.; Gopalan, A.; Xiong, X. The characterization of deep convective cloud albedo as a calibration target using MODIS reflectances. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization, Incheon, Korea, 4 November 2010; Volume 7862. [Google Scholar]
- Bhatt, R.; Doelling, D.R.; Scarino, B.R.; Gopalan, A.; Haney, C.O. An initial assessment of the VIIRS onboard calibration using DCC and desert referenced to the Aqua-MODIS calibration. In Proceedings of the Earth Observing Systems XVIII, San Diego, CA, USA, 23 September 2013; Volume 8866, p. 88660K. [Google Scholar]
- Uprety, S.; Cao, C.; Blonski, S. Retrospective analysis of Suomi NPP VIIRS radiometric bias for reflective solar bands due to operational calibration changes. Int. J. Remote Sens. 2010, 37, 5472–5489. [Google Scholar] [CrossRef]

















| Versions | Time Period | Status | Solar Irradiance Model Used | Reference | Comments |
|---|---|---|---|---|---|
| Operational | October 2011–present | Operationally produced and archived on CLASS | Modtran 4.3 | [4] | Not consistent. Early data have many artifacts |
| RSBautocal | January 2012–May 2020 | Calibration coefficients regenerated but data not reprocessed | Modtran 4.3 | [15] | |
| Version 1 (removed Oscillation) | January 2012–May 2020 | Incorporated in version 2 bias correction | Modtran 4.3 | [27] | |
| Hybrid (OC F-factor) | January 2012–March 2017 | Generated by NOAA OC group for solar bands | Modtran 4.3 | [22] | |
| V1.9 (using MODTRAN solar irradiance) | November 2011–March 2018 | Calibration coefficients regenerated but data not reprocessed | Modtran 4.3 | [27] | |
| Kalman V2.0 | January 2012–May 2020 | Reprocessed and ready for distribution | Thuillier 2003 |
| Calibration Method | Advantages | Limitations |
|---|---|---|
| Onboard Solar Diffuser w/Solar diffuser stability monitor (SDSM) | Frequent calibration (up to once per orbit); not affected by atmosphere; uniform and stable; absolute accuracy based on uncertainty budget analysis | Diffuser itself degrades over time; residual degradation may not be accounted for even with the SDSM; NIR bands (M8-M11, I3) not covered by SDSM |
| Lunar calibration | Lunar reflectance is extremely stable; monthly lunar calibration maneuver at same lunar phase angle can reduce uncertainties in stability down to sub-percent level in time series | Only 9 out of 12 months lunar cal is achievable (summer gap due to large spacecraft roll angle); each month only has one datapoint; requires longer time period (at least one year) to detect trend. |
| Desert/vicarious site calibration | Desert sites reflectance are considered pseudo-invariant; more accessible for all satellites; ground validation is possible | Atmospheric effect still exists; site bidirectional reflectance distribution function (BRDF) effect introduces seasonal uncertainties; site may not be stable; cloud contamination reduces the number of useable samples. Not all sites are suitable. |
| SNO inter-satellite calibration | Compares calibration with those from other satellites with low uncertainties using coincident observations | Limited to the polar regions for polar -orbiting satellites; extension to low latitudes compromises view angle and time widow; absolute values not established. |
| Deep convective clouds | Not affected by atmosphere due to height; bright and stable, spectrally relatively flat in the visible spectrum; more accessible globally. | Clouds have no fixed location or shape; relies on large sample statistics to reduce uncertainties; absolute reflectance affected by BRDF |
| Solar Calibration | Lunar Calibration | DCC | SNOx | Desert | |
|---|---|---|---|---|---|
| Data Frequency | Every orbit | Monthly with 3–4 months gap each year | Monthly | At most 8 days and affected by cloud contamination. | At most 16-days and affected by cloud contamination. |
| Starting Date | 8 November 2011 | 2 April 2012 | 15 February 2012 | 8 January 2012 | 18 January 2012 |
| Monthly DCC Reflectance (Operational) | Monthly DCC Reflectance (Reprocessed) | |||||
|---|---|---|---|---|---|---|
| Avg. | SD (%) | Trend (%/year) | Avg | SD (%) | Trend (%/year) | |
| M1 | 0.949 | 0.8 | −0.19 | 0.947 | 0.5 | −0.01 |
| M2 | 0.939 | 0.9 | −0.44 | 0.939 | 0.4 | −0.00 |
| M3 | 0.936 | 0.8 | −0.35 | 0.935 | 0.5 | 0.11 |
| M4 | 0.907 | 0.7 | −0.30 | 0.908 | 0.4 | 0.08 |
| M5 | 0.935 | 0.4 | −0.08 | 0.929 | 0.4 | 0.05 |
| M7 | 0.924 | 0.4 | 0.07 | 0.919 | 0.2 | 0.02 |
| M8 | 0.698 | 0.9 | 0.06 | 0.688 | 0.5 | −0.00 |
| M9 | 0.626 | 1.6 | 0.11 | 0.609 | 1.1 | 0.00 |
| M10 | 0.232 | 2.9 | 0.11 | 0.228 | 1.7 | −0.04 |
| M11 | 0.371 | 2.1 | 0.09 | 0.368 | 1.3 | 0.00 |
| I1 | 0.898 | 0.5 | −0.14 | 0.900 | 0.4 | 0.05 |
| I2 | 0.925 | 0.5 | −0.21 | 0.920 | 0.3 | 0.03 |
| I3 | 0.234 | 3.0 | −0.10 | 0.229 | 1.7 | −0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Zhang, B.; Shao, X.; Wang, W.; Uprety, S.; Choi, T.; Blonski, S.; Gu, Y.; Bai, Y.; Lin, L.; et al. Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies. Remote Sens. 2021, 13, 1075. https://doi.org/10.3390/rs13061075
Cao C, Zhang B, Shao X, Wang W, Uprety S, Choi T, Blonski S, Gu Y, Bai Y, Lin L, et al. Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies. Remote Sensing. 2021; 13(6):1075. https://doi.org/10.3390/rs13061075
Chicago/Turabian StyleCao, Changyong, Bin Zhang, Xi Shao, Wenhui Wang, Sirish Uprety, Taeyoung Choi, Slawomir Blonski, Yalong Gu, Yan Bai, Lin Lin, and et al. 2021. "Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies" Remote Sensing 13, no. 6: 1075. https://doi.org/10.3390/rs13061075
APA StyleCao, C., Zhang, B., Shao, X., Wang, W., Uprety, S., Choi, T., Blonski, S., Gu, Y., Bai, Y., Lin, L., & Kalluri, S. (2021). Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies. Remote Sensing, 13(6), 1075. https://doi.org/10.3390/rs13061075