Next Article in Journal
Analyzing the Suitability of Remotely Sensed ET for Calibrating a Watershed Model of a Mediterranean Montane Forest
Next Article in Special Issue
Remote Sensing of Lake Water Clarity: Performance and Transferability of Both Historical Algorithms and Machine Learning
Previous Article in Journal
Land Subsidence in Wuhan Revealed Using a Non-Linear PSInSAR Approach with Long Time Series of COSMO-SkyMed SAR Data
Previous Article in Special Issue
Spatial Heterogeneity in Dead Sea Surface Temperature Associated with Inhomogeneity in Evaporation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 7
10.3390/rs13071257
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Landsat 8 Lake Water Clarity Empirical Algorithms: Large-Scale Calibration and Validation Using Government and Citizen Science Data from across Canada

by
Eliza S. Deutsch
1,*,
Jeffrey A. Cardille
2,
Talia Koll-Egyed
3 and
Marie-Josée Fortin
1
1
Department of Ecology and Evolutionary Biology, University of Toronto, 25 Willcocks Street, Toronto, ON M5S 3B2, Canada
2
Department of Natural Resources Sciences and Bieler School of Environment, McGill University, Macdonald-Stewart Building, Montreal, QC H9X 3V9, Canada
3
Department of Natural Resources Sciences, McGill University, Macdonald-Stewart Building, Montreal, QC H9X 3V9, Canada
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(7), 1257; https://doi.org/10.3390/rs13071257
Submission received: 26 February 2021 / Revised: 22 March 2021 / Accepted: 24 March 2021 / Published: 26 March 2021
(This article belongs to the Special Issue Remote Sensing of Lake Properties and Dynamics)
Browse Figures
Versions Notes

Abstract

:
Water clarity has been extensively assessed in Landsat-based remote sensing studies of inland waters, regularly relying on locally calibrated empirical algorithms, and close temporal matching between field data and satellite overpass. As more satellite data and faster data processing systems become readily accessible, new opportunities are emerging to revisit traditional assumptions concerning empirical calibration methodologies. Using Landsat 8 images with large water clarity datasets from southern Canada, we assess: (1) whether clear regional differences in water clarity algorithm coefficients exist and (2) whether model fit can be improved by expanding temporal matching windows. We found that a single global algorithm effectively represents the empirical relationship between in situ Secchi disk depth (SDD) and the Landsat 8 Blue/Red band ratio across diverse lake types in Canada. We also found that the model fit improved significantly when applying a median filter on data from ever-wider time windows between the date of in situ SDD sample and the date of satellite overpass. The median filter effectively removed the outliers that were likely caused by atmospheric artifacts in the available imagery. Our findings open new discussions on the ability of large datasets and temporal averaging methods to better elucidate the true relationships between in situ water clarity and satellite reflectance data.

Graphical Abstract

1. Introduction

Obtaining a global perspective of changing freshwater quality is crucial in managing the multiple essential water resource uses in the face of contemporary shifting climate and land-use dynamics. The constraints of in situ lake monitoring, including access to remote locations and effective funding for large and comprehensive sampling programs, have been increasingly overcome through low-cost satellite remote sensing applications to map broad-scale freshwater-quality trends in space and time. This is particularly true as more satellite imagery becomes freely available and as tools, such as Google Earth Engine [1], provide platforms for mass processing of image data to effectively assess large-scale patterns.
Nonetheless, the remote sensing of inland freshwater quality remains challenging and incongruent due to the relatively small size of the majority of the world’s lakes and reservoirs, and due to the optical complexity of Type II water bodies [2,3]. Spatial constraints that are introduced by the large pixel sizes of the historic ocean color sensors (such as MERIS, MODIS, and SEAWIFS) have been overcome by applications of higher resolution sensors, such as those aboard the SPOT [4,5], Landsat [6,7,8,9,10], and, most recently, Sentinel-2 [6,11,12] satellites, and CubeSat constellations, such as PlanetScope [13,14,15], despite band designations for these sensors being optimized for extracting information from land surfaces, rather than water features [2,16]. Optical complexity constraints to traditional bio-optical modeling, including more convoluted optical signals from the diverse water column constituents of Type II waters, as well as a lack of sufficient data on inherent optical properties in many locations, has resulted in the wide application of empirical modeling to extract freshwater quality information from satellite imagery [7,8,10,16,17].
Empirical modeling most often proceeds through statistical regression, relating visible or near-infrared (NIR) spectral bands or band ratios to optically active in situ water column characteristics, such as water clarity [8,9,12,16,18,19]. These models have traditionally been calibrated locally within a distinct geographical area [20,21,22,23,24,25,26,27] or in a specific water body [6,7,28,29,30,31], with temporal matching between the in situ sampling date and satellite overpass generally one day and up to a maximum of one week apart [8,12,20,22,32,33]. As such, most freshwater quality remote sensing studies rely on carefully timed in situ sampling programs to capture the lake conditions mirrored in a nearly simultaneous satellite image in order to minimize the error incurred from expected natural variation in water quality and water optics. The applications of resultant algorithms have also been constrained to the specific spatial and seasonal conditions of the calibration dataset [24,25,34,35].
As satellite imagery becomes increasingly accessible, and as computer infrastructure and interactive data servers make mass processing of satellite data possible at new levels of efficiency and speed [1,36], there is a new opportunity to re-evaluate traditional empirical calibration methods with very large datasets. Data filters, for example, can be explored as a way to limit the impacts of inevitable remote sensing data outliers that are caused by haze. One such data filter simply involves taking the median image value [37,38] over a set time period. Applying these filters using different time window sizes allows for us to test the temporal assumptions in algorithm calibration by assessing temporal bounds for adding more data to the algorithm development process. Understanding the impact of ever broader temporal windows also provides the opportunity to use less conventional data sources in the calibration process, including large-scale government and citizen-science monitoring efforts, where finding a close temporal match between the dates of in situ sampling and dates of cloud-free satellite imagery may be difficult [12,39].
In Canada, multiple provincial government and citizen science programs provide time-series data for several thousand lakes across the country, reaching as far back as the 1950s. Canada has more than 50% of the world’s natural lakes, with almost 900,000 lakes > 10 ha [40], yet the water quality in the vast majority of these water bodies remains uncharacterized due to the sheer number of lakes and access issues in remote locations. Canada also has a wide variety of lake types, ranging from rocky, biologically unproductive lakes of the Boreal Shield, to semi-arid and biologically productive lakes in the prairies, and, therefore, it represents a unique opportunity to comprehensively assess how spatial variability in lake optical properties impacts satellite reflectance signals. Particularly, this large data resource allows for us to explore the stability of empirical algorithms across diverse lake regions.
Although recent sensors, such as Sentinel-2, are more fine-tuned for water applications, Landsat still remains an important option given its long historical run and, thus, prospective for reconstructing historical data records. If the objective of remote sensing algorithm development is to help fill spatial and temporal data gaps in lake quality datasets, the Landsat program still remains an extremely valuable satellite resource for Type II water bodies. To improve the ultimate applicability of these remote sensing empirical algorithms for monitoring and management questions, we used a very large dataset across all 10 provinces of Canada (1) to assess the existence, extent, and geographical boundaries for regional differences in water clarity remote sensing empirical algorithm coefficients across diverse lake optical types and ecozones, and (2) to assess whether model fit information can be gained using different temporal matching windows between the date of in situ sampling and the date of satellite overpass, and from using data filtering regimes. For this study, model calibration proceeds through the regression of Landsat 8 OLI visible band ratios on in situ Secchi disk depth (SDD) data from provincial-level government and citizen science monitoring efforts. The models are validated with SDD measurements that were taken by the NSERC Canadian Lake Pulse Network, a three-year highly controlled sampling program designed to develop an in-depth characterization of lake health across the country [41].

2. Materials and Methods

2.1. Study Area

It is estimated that there are around 900,000 lakes greater than 10 ha in Canada, which collectively cover over 7% of the surface area of the country [40]. Most of these lakes, particularly in the north of the country, remain completely inaccessible to all but air travel and, therefore, have never been sampled. As such, datasets used and inferences made in this study are limited to lakes in the ten provinces within the southern half of the country. These lakes are spread over seven ecological zones (ecozones) (Figure 1), which are broad geographical classifications of landscapes in Canada that account for biological, climatological, and geological variability across the country. Table 1 summarizes lake characteristics by ecozone. The Pacific Maritime is located in the far west of the country and it is characterized by significant precipitation and mountainous topography. The Montane Cordilleran, while also mountainous, is generally drier in climate than the Pacific Maritime. To the east of the major mountain ranges lies the Prairies and Boreal Plain, flatter regions that are characterized by herbaceous vegetation, sedimentary geological foundations, and often mesic or even semi-arid climate conditions. The Boreal Shield, the largest ecozone in Canada, occupies the center of the country, with temperate climate conditions, characteristic thin soils and exposed ancient rock formations, characteristic coniferous forests, and a high density of lakes. The Mixed Wood Plains lies in the southeast of the country, and it is one of the most populated regions of Canada due to its relatively milder climate and more productive soils for agriculture, but has a far lower density of small and medium sized lakes than the Boreal region to the north. Finally, the Atlantic Maritime lies on the eastern side of the country and it is characterized by an ancient mountain range that extends down along the eastern edge of the United States. For the purposes of this study, lakes in the Pacific Maritime and Montane Cordilleran are lumped together for subsequent analysis due to smaller sample sizes and similar characteristics, as were lakes in the Boreal Plain and Prairies.

2.2. In Situ Data

Secchi disk depth (SDD), a half-white/half-black disk that is submerged into water to test clarity, is one of the most consistently measured water quality parameters in broad scale government and citizen science lake sampling programs, due to its low cost and easy-to-replicate methodology. SDD acts as an effective proxy for water quality, as it is impacted by the presence of algae (chlorophyll-a), zooplankton, suspended solids, and color dissolved organic matter (CDOM) [42,43]. It is also often used as an indicator of lake trophic state or eutrophication status [44,45] and, therefore, can be linked to concepts of lake health and ecosystem services [46].
To explore empirical SDD algorithms for lakes across Canada, an extensive data-compilation effort was undertaken, which resulted in the amalgamation of data from the British Columbia Lake Monitoring Program, Alberta Environment and Parks, Ontario Broad Scale Monitoring Program, Ontario Lake Partners Program, Quebec Volunteer Lake-Monitoring Program, New Brunswick Department of the Environment, and data obtained from the University of Saskatchewan and the online water quality data suppository waterrangers.ca. Most of the provincial sampling programs extend back in time to well before the launch of Landsat 8 in 2013, yet, for this study, the data were constrained to the Landsat 8 operational period (2013–2019). The data were further constrained to a summer seasonal window (15 June to 15 September) to restrict the analysis to summer/peak temperature and growing season/summer stratified conditions in the sample lakes. The repeat samples from the same lake were accepted as separate data points for initial algorithm development, as we are primarily interested in the optical relationship between the in situ point and the Landsat 8 band pixel reflectance values, and, therefore, data points can be viewed as being statistically independent from each other. This is particularly true, as lakes are non-static systems where water clarity conditions at a sampling station can vary over short time intervals in response to wind, water currents, nutrients, and sediment load patterns and processes [47,48,49]. A total of 8655 unique sample points were available for screening against geographically matched cloud-free Landsat 8 images in the image processing steps shown below. Upon initial processing, 2548 unique sampling points were matched within seven days of an available cloud-free image. Exploratory data analysis identified 10 potential outliers from this dataset, mostly consisting of very high in situ SDD or Landsat 8 Blue/Red values. Once these large outliers were removed, the in situ SDD values in this study fell between 0.1 m to 15 m, with a median SDD for the entire dataset of 3.48 m, representing mesotrophic conditions [44].
Figure 1 shows the distributions of SDD values per unique sampling point within the different ecozones represented in this study. SDD tended to be highest in the Pacific Maritime and Montane Cordilleran (clearest water conditions) (median SDD = 6.4 m) and lowest in the Boreal Plains and Prairies (most turbid water conditions) (median SDD = 1.3 m). The Pacific Maritime and Montane Cordilleran also had the largest range of SDD values, while the Boreal Plains and Prairies had the smallest range. The three ecozones to the east all had similar distributions and similar median SDD values to each other (Boreal Shield median SDD = 3.7 m, Mixedwood Plain median SDD = 3.6 m, Atlantic Maritime median SDD = 3.5 m), with most of the sample points in this study occurring in the Boreal Shield. In total, 22.5% of the sample stations assessed across all ecozones had more than four repeat samples over the study period (2013–2019), and Figure 2 graphs intra-sample station SDD variability for these lake stations. The variability per sample station was generally consistently high in the Pacific Maritime and Montane Cordilleran, and consistently low in the Boreal Plain and Prairies. The three ecozones to the east (Boreal Shield, Mixedwood Plains, and Atlantic Maritime) all had some stations with relatively high variability and some stations with relatively low variability, indicating that other factors than ecozone characteristics play strong roles in per lake SDD fluctuations in these regions.
Provincial data sources were supplemented with SDD measurements from the NSERC Canadian Lake Pulse Network. The Lake Pulse Network is an academic-government research partnership that is designed to provide Canada’s first national-level assessment of lake health [41]. Three summer (1 July 10 September) field seasons (2017–2019) of comprehensive limnological studies resulted in the measurement of multiple water quality parameters in approximately 680 lakes across the country. Each lake was only sampled once during the campaign. Water clarity, as SDD, was measured in both the morning and afternoon, with the mean values for lakes used in this study. Lake Pulse data is known to be of high quality due to extensive training of field personnel, and therefore is used in this study as a validation dataset against the potentially less precise citizen science efforts. It is important to note that the validation dataset remains independent of the model calibration dataset, as different lakes were sampled in the different campaigns (no repeat samples). Although Lake Pulse field crews sampled lakes in the 10 Canadian provinces and two territories (Yukon and Northwest Territories), only provincial data (sample size = 592), representing the southern portion of Canada, was used for validation in this study due to limited sample stations and the lack of provincial data for the northern locations. Therefore, the algorithm results are only applicable to lakes in the southern half of the country (colored area in Figure 1A).
Figure 3 shows the data available for calibration (provincial government and citizen science sources) and validation (Lake Pulse). Sample stations in the calibration dataset (green points) were the densest in the southeast of the country in the Mixedwood Plain ecozone and in the southeastern portion of the Boreal Shield ecozone. Good distribution of data was also apparent in the western half of the country. Data gaps in the middle of the country are due to limited government lake monitoring programs in the provinces of Saskatchewan and Manitoba. Limited calibration data in the northern portions of Ontario and Quebec (provinces in the center-east of the country) are due to a lack of roads and access points to most lakes in these areas. The Lake Pulse dataset (validation dataset shown as orange points in Figure 3) was more evenly distributed across the study area due to careful sample design to more effectively characterize lake health status across the southern part of the country. Nonetheless, parts of Ontario and Quebec still remain unsampled due to difficulty of access issues. The higher proportion of Lake Pulse sampling stations in the Prairie and Boreal Plain ecozones likely explains the higher proportion of low SDD values in this dataset relative to that of the citizen science (Figure 3 histogram). Nonetheless, both of the datasets contain a similar range of available SDD values for both calibration and validation.

2.3. Image Processing

For the remote sensing algorithm development, we used Landsat 8 images from the U.S. Geological Survey (USGS) Surface Reflectance Product, with band reflectance values being extracted using Google Earth Engine (GEE) [1]. The atmospheric correction of these images is based on the Landsat 8 Surface Reflectance Code (LaSRC), which uses an internal radiative transfer model with input from a MODIS climate modeling grid, and digital elevation that is derived from GTOPO5 [50]. Further atmospheric correction can often be helpful due to the difficulty of extracting correct surface reflectance from darker objects, such as water bodies, yet most of the correction methods require information on inherent optical properties that are difficult to obtain for remote lakes. The LaSRC has been compared to other atmospheric correction regimes, including MAIN [51], ATCOR, and FORCE [52], and it has been found to perform favorably. The Landsat 8 surface reflectance images also include standard geometric and terrain correction.
To assess regional/spatial boundaries for calibrating regression coefficients between the in situ SDD measures and Landsat 8 surface reflectance, a temporal window of seven days between field measure and satellite overpass was applied given its acceptance in the literature [8,20,22,32]. A one-day window between the date of in situ sample and the date of satellite overpass was also used to test regional/spatial coefficient boundaries, as eutrophic and mesotrophic lakes may be susceptible to more rapid changes due to short-term weather events and associated nutrient enrichments. Only images with less than 50% cloud cover were processed in an initial screening of data in GEE. Next, a 60 m buffer was applied around the in situ sampling point coordinates, with pixel values within the buffer being averaged to represent point reflectance values. Note that, although buffering it is a common practice in remote sensing studies, the assumption that the buffer represents the point measurement can introduce errors of scale mismatch [53]. Pixel-values that were extracted from the buffer zone were then closely examined for data quality and further evidence of cloud cover by assessing band reflectance values as well as the quality band (‘pixel_qa’) values from the Landsat 8 surface reflectance product. All of the images with negative reflectance values in the visible and NIR region were removed from the analysis, as were all ‘pixel_qa’ values that indicated cloud probabilities (only pixel-qa = 324 was accepted) [54]. For in situ data that matched to two or more images within the seven-day temporal window (as a result of scene overlap), the median value of their reflectance was used. In total, 1513 unique sampling points were available for algorithm calibration using the seven-day time window approach, and 403 unique sampling points were available for algorithm calibration using the one-day time window approach.
Once regional patterns were examined and effective spatial boundaries defined for algorithm calibration, temporal bounds for effectively capturing the relationship between in situ measurements and cloud-free images were assessed by applying a median filter on ever-wider time windows (and, thus, incorporating ever increasing satellite reflectance information into the analysis). Median filtering can potentially improve algorithm fit through removing image outliers that are caused by atmospheric effects. The temporal windows used for this analysis are defined, as follows:
  • Same Day: image reflectance within a one-day time window of the in situ sample date for each sample station regressed against the in situ sample.
  • Same Week: median (from scene overlap if applicable) image reflectance within a seven-day time window of the in situ sample date for each sample station. This was regressed against the in situ sample per sample date.
  • Same Month: median image reflectance within a 30-day time window of the in situ sample date for each sample station. This was regressed against the median of the in situ samples within the same 30-day time window for a given sample station.
  • Same Year: the median image reflectance within the same summer the in situ sample was taken for each sample station. This was regressed against the median of the in situ samples within the same summer window for a given sample station.
  • All Years: median satellite band ratio of all available images through the Landsat record (2013–2019) regressed against the median of all repeat in situ samples of a single sample station over that same time period (2013–2019).
Note that repeat lake measurements only occurred for a portion of the lakes, the median values of in situ samples for the Same Month, Same Year, and All Years time windows described above often only represent a single measurement (39.5% of sample stations only have 1 in situ measurement, 24.0% of sample stations have two repeat measurements, 14% have three repeat measurements, and 22.5% have four or more repeat measurements).
All of the images for the temporal window analysis were screened identically to the procedure that is described above for the spatial analysis of coefficient fit. A total of 2755 images were processed representing 59,774 unique sample points for 978 lake sample stations across the Landsat 8 image record (2013–2019) for the provincial calibration dataset, and a total of 3938 images were processed representing 14,475 unique sample points for 592 lake sample stations across the Landsat 8 image record for the Lake Pulse validation dataset.

2.4. SDD Algorithm Calibration

The band ratios are often used for remote sensing empirical algorithm development with Landsat images as band ratios tend to eliminate noise in the reflectance signal originating from underlying water body optical characteristics [55,56]. There have been many studies assessing optically active water quality constituents using Landsat images, so much is already known regarding how bands respond to the optical signals of water clarity. In the Landsat literature, certain band ratios have shown to be quite effective across diverse lake clarity systems. This is the case for the Landsat Blue/Red ratio, which has repeatedly proved effective in estimating water clarity/ SDD readings in diverse water body types across North American and the world [8,12,16,28,32,35,57], with clarity levels ranging from 0.1–15 m. Generally, reflectance in the blue band decreases in turbid waters, while reflectance correspondingly increases in the red band [12,20,57,58]. Given the consistent success of this particular algorithm in the literature, we can now start to build upon this previous work and begin asking questions about spatial patterns at large geographical scales. As such, we proceed with testing regional/ spatial variation in algorithm coefficients while using this simple, parsimonious Blue/Red model. This allows for us to clearly assess patterns and understand the results within the context of a large existing literature.
Initial data exploration identified a number of potential outliers. These outliers were removed from subsequent analysis, as we are primarily interested in assessing the average conditions and general patterns in lake water clarity optics in this study. There is a strong likelihood that outliers represent atypical conditions, either in the lake itself or in atmospheric conditions. Log transformation of SDD and the predictor (Landsat 8 Blue/Red) was necessary to meet the assumptions of parametric regression. The final form of the tested algorithm for the first step of analysis was ln(SDD) = β0 + β1(ln(Blue/Red)) + ε, where β0 is the regression intercept, β1 is the coefficient for the independent variable, and ε is the error term.
Spatial patterns in regression coefficients were assessed using two methods. First, the model fit and model coefficients for in situ SDD by the Landsat 8 Blue/Red band ratio were compared for the different ecozones of Canada. Second, a global regression for all sample points across Canada was developed and residuals were mapped and graphed to assess the geographic clustering of extreme residual values.
The best regression models incorporating geographical boundaries/spatial differences were then re-assessed to see whether model fit could be improved by the addition of an extra single band term (Blue, Green, Red and NIR) or by the use of more complex polynomial models (second, third, and fourth degree polynomials). The addition of an extra single band is common in the SDD empirical remote sensing literature [8,12,22,28,35]. Except for the polynomial models, we restricted the test models to the addition of only a single extra term in order to avoid overfitting the models. We looked for significant improvement in model fit (R2, RMSE and bias) to adopt the more complex algorithm forms, as we are primarily interested in comparable and general patterns of model structure in this study.
Finally, algorithm improvement through median filtering on ever-broader temporal windows (as described above) was also tested to see whether this could increase the model fit above and beyond the addition of extra model terms or more complex model forms. Differences in model fit for these different temporal-window regressions were compared using model R2, root mean square error (RMSE), and statistical bias using the metrics package [59] in the software R [60].

2.5. SDD Algorithm Validation

The final models were fully validated with the separate dataset from the NSERC Canadian Lake Pulse Network. A four-fold (k-fold) cross-validation was also performed on the citizen science data using the DAAG package [61] in the software R [60]. The data were partitioned into k equal subsamples per model, with one subsample being used for validation and three used as training data. This process was repeated four times, so that each subsample was used once for validation. R2 shrinkage was assessed for the cross-validation models using the bootstrap package [62].

3. Results

Regressions that were run between in situ SDD and Landsat Blue/Red band ratios for the different ecozones generally showed better R2 values for the one-day temporal window between the date of in situ sample and the date of satellite overpass as compared to results for the seven-day temporal window, although the RSME values were lower for the seven-day window (Table 2). The model coefficients varied for the one-day window, where less data were available, but were generally more consistent using the seven-day window (except for the boreal shield), where significantly more data points were available to test patterns. Except for the Atlantic Maritime, the model coefficients were slightly higher (steeper slopes) for the one-day window than for the seven-day window. All of the data for the one-day window and the seven-day window were plotted on a single graph as well as individual ecozone graphs in Figure 4 and Figure 5. Although different ecozone data clustered in different parts of the main distribution, both the results depicted in the one-day window and seven-day window Figures suggest that all points, regardless of ecozone, effectively fit within a single data distribution. These results indicate that the relationship between in situ SDD and Landsat 8 Blue/Red was consistent across wide ranging lake optical types throughout the entire southern portion of Canada.
Proceeding with a global regression model using the seven-day temporal window (ln(SDD) = 0.59 + 1.56*ln(Blue/Red), p-value < 0.0001, R2 = 0.467), the regression residuals were mapped to assess the existence of any spatial patterns in extreme residual values that fall outside of ecozone boundaries. Figure 6 shows both unstandardized residuals (in the histogram) and standardized residuals (plotted on the map) for this global model. Unstandardized residuals follow a normal distribution, with most of the unstandardized residuals falling within −1 m and 1 m, and the median being centered slightly above 0 m. Most of the standardized residuals fall within 1.96 standard deviations of the mean in this study, with little apparent spatial pattern in how extreme positive (blue points) and negative (red points) standardized residuals are distributed across the country. High and low residuals both occur in all tested ecozone groupings.
Because our initial spatial assessment indicated that no clear geographical boundaries exist in the application of algorithm coefficients for the Blue/Red band ratio model, a single global model, incorporating data from all ecozones, was used as a base to test the model improvement through the addition of extra terms or the use of more complex polynomial model forms. Table 3 shows the results from these tests, using the seven-day temporal window. Single band models all showed a slight improvement in model fit (particularly in bias and adjusted R2 values), with the best model incorporating the addition of the green single band (bias = 0.349, adjusted R2 = 0.504). Polynomial models showed a progressive improvement in adjusted R2 with model complexity, but they also showed an increase in model bias with model complexity. Improvements in RMSE were minimal for all tested models, falling from 1.87 to a minimum of 1.85. Given the limited model improvements with the more complex model forms, we decided to proceed with the assessment of median filtering on ever increasing temporal windows using the original single band ratio model (Blue/Red) in order to simplify the results and improve comparability with other studies.
Table 4 shows the regression models for the five different median filter temporal window sizes with the global regression of natural logarithm transformed SDD on natural logarithm transformed Landsat 8 Blue/Red. Model fit significantly improved when increasing imagery data input from the median of ratios for one day (R2 = 0.421) or one week (R2 = 0.47) to the median for one month (R2 = 0.51) and median for one year (R2 = 0.51), and then again to the median for summer observations from all years (R2 = 0.65). Bias also decreased significantly with increasing temporal window sizes, as did the RMSE, except for a slight increase in RMSE between the median of the same year and median of all years models. Figure 7 plots data for the different temporal windows. With progressively increasing temporal windows, the data distribution clearly tightens around the line of best fit, indicating the removal of problematic sample points through median filtering. The model coefficients (slope) also increased with median filters on larger temporal window sizes, with low SDD values tending to be overestimated and larger SDD values underestimated in models using smaller time windows as compared to models using larger time windows (Figure 7). Increasing the slope with median filtering over larger time windows improved model estimation of low SDD values, but very low values (SDD < 1 m) remained overestimated by all the models.
Figure 8 shows the validation of median filtering results using the separate dataset generated by the LakePulse program. The LakePulse dataset has a larger proportion of low SDD values (see Figure 3) than the calibration dataset, which clearly highlights the poor performance of all median filter models at effectively predicting values of SDD < ln(0) (SDD < 1 m). These low values of SDD are consistently overestimated, although the degree of overestimation decreases with increasing temporal window size. Nonetheless, the models, particularly using median filtering on the one-month, single season, and all years time windows, were able to effectively estimate the observed SDD for values greater than 1 m. The tightest estimate of SDD around the 1:1 line was found in the model using median data from all years. The poorest performance was found in the model using data from the same day of satellite overpass.

4. Discussion

The results of this study demonstrate that using very large imagery datasets can give new insight into the calibration of Landsat 8 water quality remote sensing empirical algorithms. The predictive power of the best model in this study can be considered to be good (R2 = 0.645 for the All Years model), despite calibration with optically variable lake types from multiple data sources. It is possible that a more water-specific atmospheric correction regime may have improved model fit by the better removal of atmospheric artifacts in the images used, but this type of assessment was outside the scope of this study. This study also confirms the effectiveness of the Landsat Blue/Red band ratio for use in estimating SDD from satellite imagery, as has been demonstrated in a number of other studies in a large variety of lake systems [8,12,16,22,28,35,57,58,63], with a combined range of SDD values that are similar to that seen in our dataset for Canadian lakes (0.1–15 m). Some of these studies found improved algorithm fit with the addition of a second single band regression term, most commonly the Blue, Green or Red band. Although expanding models with the addition of a second band term, especially the addition of the Green band, resulted in small improvements in model fit in this study, these improvements were only minor when compared to the improvement that is seen with using more imagery in our tests of median filtering techniques. Given the minor improvements from expanded models, they would have also provided comparable consistency in the median filtering tests as to what we found using the most parsimonious Blue/Red model form. Recent published studies are now using machine learning [51,64] and novel spectra processing techniques [65] to improve algorithm fit for the extraction of other optically active water column constituents (chlorophyll-a, total suspended solids, and color dissolved organic matter), and it would be interesting in future work to see how such modeling techniques that are applied to the extraction of Secchi disk depth compare to the more parsimonious model form that we used, and how these newer techniques would also respond to the median filtering methods applied here.
In this study, data from a wide variety of lake types across Canada, including deep oligotrophic lakes on the west coast, eutrophic prairie pothole lakes in the central plains, and glacial scour lakes of the boreal region, all appear to cluster in a single distribution when in situ SDD is graphed against the Landsat 8 Blue/Red bands. This result was unexpected, particularly as previous studies have most often been calibrated locally for individual lakes or regions of similar lakes [6,19,20,21,23,25,26,30] and, thus, algorithm calibration has generally only been tested across a more limited range of lake optical types and SDD values than attempted in this study. When tested individually, different Canadian ecozone groupings showed some differences in the model coefficients and model fit, likely due to more limited spread in in situ SDD values that ultimately obscured the main trend apparent once individual regions were visualized within the entire dataset. This was particularly true for lakes of the Boreal Shield ecozone, which had a more moderate range of Secchi depths and a less obvious distribution trend when assessed alone. These results may have important implications for exploring more universal patterns in water clarity optics, and exploring the usefulness of large sample sizes over larger regions for discerning true trends in the spectral relationships.
Nonetheless, the global model only performed well for SDD > 1 m, as seen in the validation procedures, or lakes that exhibit oligotrophic to mesotrophic conditions according to Carlson’s trophic index [44]. The global model tended to over-predict SDD in the higher eutrophic to hypereutrophic range and, thus, was unable to predict the extent of eutrophication, although the model was able to distinguish whether a lake had reached a threshold of high trophic status/low clarity (i.e., SDD < 1 m). The trend of model overestimation of SDD > 1 m is clearly apparent in Figure 8, as the validation dataset for this study had a larger proportion of low value or eutrophic SDD data points than the calibration dataset. Low water clarity in lakes can be influenced by several optically active water body constituents, including chlorophyll-a, suspended sediment, and color dissolved organic matter (CDOM), which may uniquely influence spectral signals [3]. Highly eutrophic lakes in Canada are often clustered in the Prairie and Boreal Plain ecozones, where clarity is influenced by a complex mix of inorganic sediments, macrophyte biomass, and phytoplankton blooms [66,67]. More research in regions with a larger variety of types of optically active water column constituents in these low clarity systems is necessary to better assess whether a more universal calibration with Landsat band ratios is possible when SDD < 1 m.
Remote sensing studies generally calibrate empirical algorithms using a short time window between in situ sampling and satellite overpass in order to optimize the similarity of conditions between the lake point measurement and image pixel [8,12,20,22,32,33]. The emphasis on short time windows assumes that water optics at the sampling point or pixel level can change significantly over the course of days or weeks, limiting the capacity of larger temporal gaps in satellite overpasses to adequately represent in-lake sampling conditions [8,32]. Nonetheless, in this study, we found that applying a median filter with ever broader time windows consistently resulted in improved algorithm fit. As time windows increased, median filtering preferentially removed data points from the upper left part of the distribution of in situ SDD against Landsat 8 Blue/Red (as seen in Figure 7), where lakes with high clarity were matched to Blue/Red ratio values more reliably associated with lower clarity lakes. This preferential point removal resulted in a steeper regression slope, thereby also improving the algorithm fit for very low clarity lakes (Figure 7). One likely reason for the model fit improvements from median filtering on large time windows is that repeat satellite data over a given location is inherently variable due to atmospheric influences such as haze [68]. Adding more data to the analysis and assessing median band ratio data may remove atmospheric artifacts that were not already filtered out through atmospheric correction and data cleaning steps. As such, it is possible that applying the median filter over wider time windows helps us to better discern the real Landsat 8 Blue/Red surface reflectance over a water area pixel. A similar improvement was also seen when applying temporal averaging for estimating color dissolved organic matter (CDOM) in a much smaller subset of lakes in eastern Canada [69].
Applying the median filter should only be effective if the following assumption is met: variability in SDD in the modeled area of the lake is less over a week, a month, a summer, or summers from 2013–2019 than is the variability in image conditions over that same time period. Restricting analysis to the summer season may have helped to reduce large fluctuations in clarity at a sampling station between years. The log transformation of data for algorithm calibration also relativizes clarity differences, such that larger differences in clear lakes have less impact on model fit than large differences in turbid lakes. Further, although lake clarity does vary over short time periods in response to nutrient and sediment release and wind and water currents, this variability is often much less than the noise inherent in satellite data. Noise in dark objects, such as water bodies, is persistent and challenging [70,71], and passing a filter over the results is therefore helpful in reducing this noise. A median filter is a simple filter that is insensitive to outliers, which is important for remote sensing imagery [37,38]. Prior to recent years, it would have been impractical to consider filtering multiple images for empirical algorithm calibration, because imagery was scarce and data acquisition and processing was expensive and time-consuming. Now that we have extensive imagery reserves and effective mass-processing servers, such as Google Earth Engine, we have the ability to consider more sophisticated treatment, such as techniques similar to what is seen in the emerging body of signal processing literature, where there are multiple observations for a given signal (e.g., [72,73,74]).

5. Conclusions

Integrating various Canadian provincial government and citizen science monitoring efforts into a large dataset allowed us to effectively demonstrate a lack of geographic variability in algorithm coefficients across diverse lake types in Canada. In general, a single global algorithm was able to effectively define SDD for lakes within boreal, prairie, mountainous, and agricultural-productive regions. The single Landsat 8 Blue/Red band ratio proved to be almost as effective as more complex models in estimating SDD across southern Canada, which raises strong possibilities for further study and comparison in other national and international contexts. Furthermore, using this large dataset along with the massive imagery data processing and server resources from Google Earth Engine allowed us to test how applying a median filter on increasing the temporal window sizes between the date of in situ data sampling and the date of satellite overpass impacted model fit. Ultimately, we demonstrated that applying the median filter to large time windows reduced some of the noise inherent in satellite reflectance signals. Models using summer season data from all years of Landsat 8 operation (2013–2019) had significantly better fit than models using other temporal windows, particularly those using one-day and seven-day temporal differences between the date of in situ sample and the date of satellite overpass. Overall, the results of this study provide readily computationally and comprehensively applicable tools and methods that water managers can use to better calibrate remote sensing empirical algorithms and ultimately better track changes in water quality over wide geographical scales.

Author Contributions

Conceptualization, E.S.D., J.A.C. and M.-J.F.; methodology, E.S.D., J.A.C., T.K.-E. and M.-J.F.; software, E.S.D. and T.K.-E.; validation, E.S.D.; formal analysis, E.S.D.; data curation, E.S.D.; writing—original draft preparation, E.S.D.; writing—review and editing, E.S.D., J.A.C. and M.-J.F.; funding acquisition, M.-J.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) Canadian LakePulse Network (Strategic Partnership Network NETG 479720-15), and NSERC Discovery Grant to Marie-Josée Fortin (#5134) and NSERC Canada Research Chair (CRC) to Marie-Josée Fortin.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Summarized data from British Columbia Lake Monitoring Program, Alberta Environment and Parks, and New Brunswick Department of Environment are available on request from the corresponding author. Data from Saskatchewan, Ontario, and Quebec, as well as validation data from Lake Pulse are available from the corresponding author only after permissions have been granted from the University of Saskatchewan, Ontario Broad Scale Monitoring Program, Ontario Lake Partners Program, Quebec Volunteer Lake Monitoring Program, and the Lake Pulse Network.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
  2. Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
  3. Shi, K.; Li, Y.; Li, L.; Lu, H. Absorption characteristics of optically complex inland waters: Implications for water optical classification. Biogeosciences 2013, 118, 860–874. [Google Scholar] [CrossRef]
  4. Dekker, A.G.; Vos, R.J.; Peters, S.W. Analytical algorithms for lake water TSM estimation for retrospective analyses of TM and SPOT sensor data. Int. J. Remote Sens. 2002, 23, 15–35. [Google Scholar] [CrossRef]
  5. Chacon-Torres, A.; Ross, L.G.; Beveridge, M.C.M.; Watson, A.I. The application of SPOT multipsectral imagery for the assessment of water quality in Lake Patzcuaro, Mexico. Int. J. Remote Sens. 1992, 13, 587–603. [Google Scholar] [CrossRef]
  6. Bonansea, M.; Ledesma, M.; Rodriguez, C.; Pinotti, L. Using new remote sensing satellites for assessing water quality in a reservoir. Hydrol. Sci. J. 2019, 64, 34–44. [Google Scholar] [CrossRef]
  7. Xu, X.; Huang, X.; Zhang, Y.; Yu, D. Long-Term Changes in Water Clarity in Lake Liangzi Determined by Remote Sensing. Remote Sens. 2018, 10, 1441. [Google Scholar] [CrossRef] [Green Version]
  8. Kloiber, S.M.; Brezonik, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ. 2002, 82, 38–47. [Google Scholar] [CrossRef]
  9. Olmanson, L.G.; Brezonik, P.L.; Bauer, M.E. Geospatial and Temporal Analysis of a 20-Year Record of Landsat-Based Water Clarity in M innesota’s 10,000 Lakes. J. Am. Water Resour. Assoc. 2014, 50, 748–761. [Google Scholar] [CrossRef]
  10. Lehmann, M.K.; Nguyen, U.; Muraoka, K.; Allan, M.G. Regional trends in remotely sensed water clarity over 18 years in the Rotorua Lakes, New Zealand. N. Z. J. Mar. Freshw. Res. 2019, 53, 513–535. [Google Scholar] [CrossRef]
  11. Kuhn, C.; de Matos Valerio, A.D.M.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Richey, J.; Stadler, P.; Crawford, J.; Striegl, R.; et al. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef] [Green Version]
  12. Page, B.P.; Olmanson, L.G.; Mishra, D.R. A harmonized image processing workflow using Sentinel-2/MSI and Landsat-8/OLI for mapping water clarity in optically variable lake systems. Remote Sens. Environ. 2019, 231, 111284. [Google Scholar] [CrossRef]
  13. Wicaksono, P.; Lazuardi, W. Assessment of PlanetScope images for benthic habitat and seagrass species mapping in a complex optically shallow water environment. Int. J. Remote Sens. 2018, 39, 5739–5765. [Google Scholar] [CrossRef]
  14. Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L.; Gege, P. Physics-based Bathymetry and Water Quality Retrieval Using PlanetScope Imagery: Impacts of 2020 COVID-19 Lockdown and 2019 Extreme Flood in the Venice Lagoon. Remote Sens. 2020, 12, 2381. [Google Scholar] [CrossRef]
  15. Vanhellemont, Q. Daily metre-scale mapping of water turbidity using CubeSat imagery. Opt. Express 2019, 27, A1372–A1399. [Google Scholar] [CrossRef] [PubMed]
  16. Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
  17. Uudeberg, K.; Aavaste, A.; Kõks, K.L.; Ansper, A.; Uusõue, M.; Kangro, K.; Ansko, I.; Ligi, M.; Toming, K.; Reinart, A. Optical Water Type Guided Approach to Estimate Optical Water Quality Parameters. Remote Sens. 2020, 12, 931. [Google Scholar] [CrossRef] [Green Version]
  18. Lymburner, L.; Botha, E.; Hestir, E.; Anstee, J.; Sagar, S.; Dekker, A.; Malthus, T. Landsat 8: Providing continuity and increased precision for measuring multi-decadal time series of total suspended matter. Remote Sens. Environ. 2016, 185, 108–118. [Google Scholar] [CrossRef]
  19. Song, K.; Liu, G.; Wang, Q.; Wen, Z.; Lyu, L.; Du, Y.; Sha, L.; Fang, C. Quantification of lake clarity in China using Landsat OLI imagery data. Remote Sens. Environ. 2020, 243, 111800. [Google Scholar] [CrossRef]
  20. Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
  21. McCullough, I.M.; Loftin, C.S.; Sader, S.A. Landsat imagery reveals declining clarity of Maine’s lakes during 1995–2010. Freshw. Sci. 2013, 32, 741–752. [Google Scholar] [CrossRef]
  22. Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
  23. Olmanson, L.G.; Brezonik, P.L.; Finlay, J.C.; Bauer, M.E. Comparison of Landsat 8 and Landsat 7 for regional measurements of CDOM and water clarity in lakes. Remote Sens. Environ. 2016, 185, 119–128. [Google Scholar] [CrossRef]
  24. Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L.; et al. Changes of water clarity in large lakes and reservoirs across China observed from long-term MODIS. Remote Sens. Environ. 2020, 247, 111949. [Google Scholar] [CrossRef]
  25. Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication changes in fifty large lakes on the Yangtze Plain of China derived from MERIS and OLCI observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
  26. Kontopoulou, E.; Kolokoussis, P.; Karantzalos, K. Water quality estimation in Greek lakes from Landsat 8 multispectral satellite data. Eur. Water 2017, 58, 191–196. [Google Scholar]
  27. Wang, S.; Li, J.; Zhang, B.; Spyrakos, E.; Tyler, A.N.; Shen, Q.; Zhang, F.; Kuster, T.; Lehmann, M.K.; Wu, Y.; et al. Trophic state assessment of global inland waters using a MODIS-derived Forel-Ule index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef] [Green Version]
  28. Deutsch, E.S.; Alameddine, I.; El-fadel, M. Monitoring water quality in a hypereutrophic reservoir using Landsat ETM + and OLI sensors: How transferable are the water quality algorithms? Environ. Monit. Assess. 2018, 190, 1–19. [Google Scholar] [CrossRef] [PubMed]
  29. Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Noges, T. First Experiences in Mapping Lake Water Quality Parameters with Sentinel-2 MSI Imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef] [Green Version]
  30. Markogianni, V.; Dimitriou, E.; Karaouzas, I. Water quality monitoring and assessment of an urban Mediterranean lake facilitated by remote sensing applications. Environ. Monit. Assess. 2014, 186, 5009–5026. [Google Scholar] [CrossRef] [PubMed]
  31. Al-Fahdawi, A.A.H.; Rabee, A.M.; Al-Hirmizy, S.M. Water quality monitoring in Al-Habbaniyah Lake using remote sensing and in situ measurements. Environ. Monit. Assess. 2015, 187, 367. [Google Scholar] [CrossRef]
  32. McCullough, I.M.; Loftin, C.S.; Sader, S.A. Combining lake and watershed characteristics with Landsat TM data for remote estimation of regional lake clarity. Remote Sens. Environ. 2012, 123, 109–115. [Google Scholar] [CrossRef]
  33. Bonansea, M.; Rodriguez, M.C.; Pinotti, L.; Ferrero, S. Using multi-temporal Landsat imagery and linear mixed models for assessing water quality parameters in Río Tercero reservoir (Argentina). Remote Sens. Environ. 2015, 158, 28–41. [Google Scholar] [CrossRef]
  34. Deutsch, E.S.; Alameddine, I. Hindcasting eutrophication and changes in temperature and storage volume in a semi-arid reservoir: A multi-decadal Landsat-based assessment. Environ. Monit. Assess. 2019, 191, 41. [Google Scholar] [CrossRef]
  35. Hicks, B.J.; Stichbury, G.A.; Brabyn, L.K.; Allan, M.G.; Ashraf, S. Hindcasting water clarity from Landsat satellite images of unmonitored shallow lakes in the Waikato region, New Zealand. Environ. Monit. Assess. 2013, 185, 7245–7261. [Google Scholar] [CrossRef] [PubMed]
  36. Kumar, L.; Mutanga, O. Google Earth Engine Applications Since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef] [Green Version]
  37. Gupta, G. Algorithm for image processing using improved median filter and comparison of mean, median and improved median filter. Int. J. Soft Comput. Eng. 2011, 1, 304–311. [Google Scholar]
  38. Chen, T.; Ma, K.-K.; Chen, L.-H. Tri-state median filter for image denoising. IEEE Trans. Image Process. 1999, 8, 1834–1838. [Google Scholar] [CrossRef] [Green Version]
  39. Lottig, N.R.; Wagner, T.; Henry, E.N.; Cheruvelil, K.S.; Webster, K.E.; Downing, J.A.; Stow, C.A. Long-Term Citizen-Collected Data Reveal Geographical Patterns and Temporal Trends in Lake Water Clarity. PLoS ONE 2014, 9, e95769. [Google Scholar] [CrossRef]
  40. Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
  41. Huot, Y.; Brown, C.A.; Potvin, G.; Antoniades, D.; Baulch, H.M.; Beisner, B.E.; Bélanger, S.; Brazeau, S.; Cabana, H.; Cardille, J.A.; et al. The NSERC Canadian Lake Pulse Network: A national assessment of lake health providing science for water management in a changing climate. Sci. Total Environ. 2019, 695, 133668. [Google Scholar] [CrossRef] [PubMed]
  42. Preisendorfer, R.W. Secchi disk science: Visual optics of natural waters. Limnol. Oceanogr. 1986, 31, 909–926. [Google Scholar] [CrossRef] [Green Version]
  43. Fee, E.J.; Hecky, R.E.; Kasian, S.E.M.; Cruikshank, D.R. Effects of lake size, water clarity, and climatic variability on mixing depths in Canadian Shield lakes. Limnol. Oceanogr. 1996, 41, 912–920. [Google Scholar] [CrossRef]
  44. Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
  45. Carlson, R.E.; Havens, K.E. Graphical Methods for the Interpretation of Relationships Between Trophic State Variables. Lake Reserv. Manag. 2005, 21, 107–118. [Google Scholar] [CrossRef]
  46. Keeler, B.L.; Polasky, S.; Brauman, K.A.; Johnson, K.A.; Finlay, J.C.; O’Neill, A.; Kovacs, K.; Dalzell, B. Linking water quality and well-being for improved assessment and valuation of ecosystem services. Proc. Natl. Acad. Sci. USA 2012, 109, 18619–18624. [Google Scholar] [CrossRef] [Green Version]
  47. Wu, G.; De Leeuw, J.; Liu, Y. Understanding Seasonal Water Clarity Dynamics of Lake Dahuchi from In Situ and Remote Sensing Data. Water Resour. Manag. 2009, 23, 1849–1861. [Google Scholar] [CrossRef]
  48. Lathrop, R.C.; Carpenter, S.R.; Robertson, D.M. Summer water clarity responses to phosphorus, Daphnia grazing, and internal mixing in Lake Mendota. Limnol. Oceanogr. 1999, 44, 137–146. [Google Scholar] [CrossRef] [Green Version]
  49. Carper, G.L.; Bachmann, R.W. Wind Resuspension of Sediments in a Prairie Lake. Can. J. Fish. Aquat. Sci. 1984, 41, 1763–1767. [Google Scholar] [CrossRef]
  50. Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
  51. Olmanson, L.G.; Page, B.P.; Finlay, J.C.; Brezonik, P.L.; Bauer, M.E.; Griffin, C.G.; Hozalski, R.M. Regional measurements and spatial/temporal analysis of CDOM in 10,000+ optically variable Minnesota lakes using Landsat 8 imagery. Sci. Total Environ. 2020, 724, 138141. [Google Scholar] [CrossRef] [PubMed]
  52. Doxani, G.; Vermote, E.; Roger, J.-C.; Gascon, F.; Adriaensen, S.; Frantz, D.; Hagolle, O.; Hollstein, A.; Kirches, G.; Li, F.; et al. Atmospheric Correction Inter-Comparison Exercise. Remote Sens. 2018, 10, 352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Heirarchical Modeling and Analysis for Spatial Data; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
  54. Sayler, K.; Zanter, K. Landsat 8 Collection 1 (C1) Landsat Surface Reflectance Code (LaSRC) Product Guide; Department of Interior U.S. Geological Survey: Sioux Falls, SD, USA, 2020. [Google Scholar]
  55. Lee, Z.; Zaneveld, J.R.V.; Maritorena, S.; Loisel, H.; Doerffer, R.; Lyon, P.; Boss, E.; Carder, K.L.; Devred, E.; Arnone, R. Remote sensing of inherent optical properties: Fundamentals, tests of algorithms, and applications. In Reports of the Internationsl Ocean-Colour Coordinating Group; Lee, Z., Ed.; International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2006; p. 89. [Google Scholar]
  56. O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Ocean. 1998, 103, 24937–24953. [Google Scholar] [CrossRef] [Green Version]
  57. Olmanson, L.G.; Brezonik, P.L.; Bauer, M.E. Evaluation of medium to low resolution satellite imagery for regional lake water quality assessments. Water Resour. Res. 2011, 47, W09515. [Google Scholar] [CrossRef] [Green Version]
  58. Nelson, S.A.C.; Soranno, P.A.; Cheruvelil, K.S.; Batzli, S.A.; Skole, D.L. Regional assessment of lake water clarity using satellite remote sensing. J. Limnol. 2003, 62, 27–32. [Google Scholar] [CrossRef] [Green Version]
  59. Hamner, B.; Frasco, M.; LeDell, E. Metrics: Evaluation Metrics for Machine Learning; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
  60. R Core Team. R: A Language and Environment for Statistical Computing. In R Foundations for Statistical Computing; R Foundations for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
  61. Maindonald, J.; Braun, W.J. DAAG: Data Analysis and Graphics Data and Functions; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
  62. Tibshirani, R.; Leisch, F. Package “Bootstrap”; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
  63. Duan, H.; Ma, R.; Zhang, Y.; Zhang, B. Remote-sensing assessment of regional inland lake water clarity in northeast China. Limnology 2009, 10, 135–141. [Google Scholar] [CrossRef]
  64. Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A machine learning approach to estimate chlorophyll-a from Landsat-8 measurements in inland lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
  65. Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel Spectra-Derived Featuers for Emperical Retrieval of Water Quality Parameters: Demonstrations for OLI, MSI, and OLCI Sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
  66. Maheux, H.M. Trends and Drivers of Water Clarity in Shallow, Prairie Lakes of Southern Alberta. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2012. [Google Scholar]
  67. Jackson, L.J.; Moquin, P.A. Turbidity of shallow prairie lakes. Lakeline 2011, 31, 36–40. [Google Scholar]
  68. Wang, D.; Ma, R.; Xue, K.; Loiselle, S.A. The Assessment of Landsat-8 OLI Atmospheric Correction Algorithms for Inland Waters. Remote Sens. 2019, 11, 169. [Google Scholar] [CrossRef] [Green Version]
  69. Cardille, J.A.; Leguet, J.-B.; del Giorgio, P.A. Remote sensing of lake CDOM using noncontemporaneous field data. Can. J. Remote Sens. 2013, 39, 118–126. [Google Scholar] [CrossRef]
  70. Jiang, H.; Feng, M.; Zhu, Y.; Lu, N.; Huang, J.; Xiao, T. An Automated Method for Extracting Rivers and Lakes from Landsat Imagery. Remote Sens. 2014, 6, 5067–5089. [Google Scholar] [CrossRef] [Green Version]
  71. Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
  72. Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process. Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
  73. Satija, U.; Ramkumar, B.; Manikandan, M.S. A Review of Signal Processing Techniques for Electrocardiogram Signal Quality Assessment. IEEE Rev. Biomed. Eng. 2018, 11, 36–52. [Google Scholar] [CrossRef] [PubMed]
  74. Wang, B.-C. Digital Signal Processing Techniques and Applications in Radar Image Processing; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 91. [Google Scholar]
Remotesensing 13 01257 g001 550
Figure 1. Histograms showing the frequency of unique sampling points per SDD (m). (A) shows the color coded ecozone map corresponding to each of the following graphs. (B–F) show histograms for each of the ecozones assessed in this study.
Figure 1. Histograms showing the frequency of unique sampling points per SDD (m). (A) shows the color coded ecozone map corresponding to each of the following graphs. (B–F) show histograms for each of the ecozones assessed in this study.
Remotesensing 13 01257 g001
Remotesensing 13 01257 g002 550
Figure 2. Boxplots showing distribution of SDD values for each sample station that had >4 repeat measurements (unique sampling points) over the study period (2013–2019). Boxes are color-coded by ecozone, consistent with previous plots. Green represents the Pacific Maritime and Montane Cordilleran, maroon represents the Boreal Plain and Prairies, purple represents the Boreal Shield, orange represents the Mixed Wood Plains, and blue represents the Atlantic Maritime.
Figure 2. Boxplots showing distribution of SDD values for each sample station that had >4 repeat measurements (unique sampling points) over the study period (2013–2019). Boxes are color-coded by ecozone, consistent with previous plots. Green represents the Pacific Maritime and Montane Cordilleran, maroon represents the Boreal Plain and Prairies, purple represents the Boreal Shield, orange represents the Mixed Wood Plains, and blue represents the Atlantic Maritime.
Remotesensing 13 01257 g002
Remotesensing 13 01257 g003 550
Figure 3. Calibration (green) and validation (orange) sampling station locations plotted on a map of Canada for the temporal window assessment. Also showing a histogram of the frequency of SDD values across the two datasets (calibration = green, validation = orange).
Figure 3. Calibration (green) and validation (orange) sampling station locations plotted on a map of Canada for the temporal window assessment. Also showing a histogram of the frequency of SDD values across the two datasets (calibration = green, validation = orange).
Remotesensing 13 01257 g003
Remotesensing 13 01257 g004 550
Figure 4. Using a one-day temporal window between the data of in situ sample and the date of satellite overpass: scatterplots of ln(SDD) versus ln(Blue/Red) for (A) all ecozones together, and (B–F) individual ecozones or ecozone groupings plotted in color over a grey cloud representing the complete dataset. Points are color-coded by ecozone, consistent with previous plots. Green represents the Pacific Maritime and Montane Cordilleran, maroon represents the Boreal Plain and Prairies, purple represents the Boreal Shield, orange represents the Mixed Wood Plains, and blue represents the Atlantic Maritime.
Figure 4. Using a one-day temporal window between the data of in situ sample and the date of satellite overpass: scatterplots of ln(SDD) versus ln(Blue/Red) for (A) all ecozones together, and (B–F) individual ecozones or ecozone groupings plotted in color over a grey cloud representing the complete dataset. Points are color-coded by ecozone, consistent with previous plots. Green represents the Pacific Maritime and Montane Cordilleran, maroon represents the Boreal Plain and Prairies, purple represents the Boreal Shield, orange represents the Mixed Wood Plains, and blue represents the Atlantic Maritime.
Remotesensing 13 01257 g004
Remotesensing 13 01257 g005 550
Figure 5. Using a 7-day day temporal window between the data of in situ sample and the date of satellite overpass: scatterplots of ln(SDD) versus ln(Blue/Red) for (A) all ecozones together, and (B–F) individual ecozones or ecozone groupings plotted in color over a grey cloud representing the complete dataset. Points are color-coded by ecozone, consistent with previous plots. Green represents the Pacific Maritime and Montane Cordilleran, maroon represents the Boreal Plain and Prairies, purple represents the Boreal Shield, orange represents the Mixed Wood Plains, and blue represents the Atlantic Maritime.
Figure 5. Using a 7-day day temporal window between the data of in situ sample and the date of satellite overpass: scatterplots of ln(SDD) versus ln(Blue/Red) for (A) all ecozones together, and (B–F) individual ecozones or ecozone groupings plotted in color over a grey cloud representing the complete dataset. Points are color-coded by ecozone, consistent with previous plots. Green represents the Pacific Maritime and Montane Cordilleran, maroon represents the Boreal Plain and Prairies, purple represents the Boreal Shield, orange represents the Mixed Wood Plains, and blue represents the Atlantic Maritime.
Remotesensing 13 01257 g005
Remotesensing 13 01257 g006 550
Figure 6. Standardized (on map) and unstandardized residuals (on histogram) for global regression model between in situ SDD and Landsat 8 Blue/Red for data taken within a one-week temporal window of each other.
Figure 6. Standardized (on map) and unstandardized residuals (on histogram) for global regression model between in situ SDD and Landsat 8 Blue/Red for data taken within a one-week temporal window of each other.
Remotesensing 13 01257 g006
Remotesensing 13 01257 g007 550
Figure 7. Scatterplots of ln(SDD) versus ln(Blue/Red) for (A) all time windows together, (B) SDD versus median Blue/Red within a 1-day window, (C) median SDD versus median Blue/Red within a 7-day window, (D) median SDD versus median Blue/Red within a 30-day window, (E) median SDD versus median Blue/Red within a single season, and (F) median SDD versus median Blue/Red over the entire Landsat 8 record (2013–2019) per sample station. Note, in graph A, lines for ‘Same Day’ (yellow) and ‘Same Week’ (purple), and lines for ‘Same Month’ (blue) and ‘Same Year’ (Orange) overlap.
Figure 7. Scatterplots of ln(SDD) versus ln(Blue/Red) for (A) all time windows together, (B) SDD versus median Blue/Red within a 1-day window, (C) median SDD versus median Blue/Red within a 7-day window, (D) median SDD versus median Blue/Red within a 30-day window, (E) median SDD versus median Blue/Red within a single season, and (F) median SDD versus median Blue/Red over the entire Landsat 8 record (2013–2019) per sample station. Note, in graph A, lines for ‘Same Day’ (yellow) and ‘Same Week’ (purple), and lines for ‘Same Month’ (blue) and ‘Same Year’ (Orange) overlap.
Remotesensing 13 01257 g007
Remotesensing 13 01257 g008 550
Figure 8. Predicted versus observed plot for SDD regression time window models: (A) SDD versus median Blue/Red within a 1-day window, (B) SDD versus median Blue/Red within a 7-day window, (C) median SDD versus median Blue/Red within a 30-day window, (D) median SDD versus median Blue/Red within a single season, and (E) median SDD versus median Blue/Red over the entire Landsat 8 record (2013–2019). Points represent the mean predicted value to the observed value for the validation dataset (Lake Pulse data). Diagonal lines represent the 1:1 line.
Figure 8. Predicted versus observed plot for SDD regression time window models: (A) SDD versus median Blue/Red within a 1-day window, (B) SDD versus median Blue/Red within a 7-day window, (C) median SDD versus median Blue/Red within a 30-day window, (D) median SDD versus median Blue/Red within a single season, and (E) median SDD versus median Blue/Red over the entire Landsat 8 record (2013–2019). Points represent the mean predicted value to the observed value for the validation dataset (Lake Pulse data). Diagonal lines represent the 1:1 line.
Remotesensing 13 01257 g008
Table
Table 1. Characteristics of lakes in Canada within ecozones represented in this study.
Table 1. Characteristics of lakes in Canada within ecozones represented in this study.
EcozoneLake OriginLake CharacteristicsLake Productivity
Pacific Maritime and Montane CordilleranMainly glacial scouring. Some tectonic processes.Sparser density, but varied characteristics.Mostly unproductive
Boreal Plain and PrairieGlacial deposition of till.Softer sedimentary rock. Formed in a thick overburden of clay, till and soil. Shallow with rapid sedimentation rates. Sometimes ephemeral Productive
Boreal ShieldGlacial scouring.Thin soils and highly weather-resistant rock. Low sedimentation rates. Large density of lakes.Unproductive
Mixed Wood PlainGlacial deposition.Formed in sedimentary rock and thick overburdens of glacial deposits. Heavily influenced by human settlement. Often productive
Atlantic MaritimeGlacial scouring.Many lakes underlain by hard igneous and metamorphosed rock. Mostly unproductive
Table
Table 2. Regression models estimating in situ SDD from Landsat 8 Blue/Red surface reflectance for different ecozones or ecozone groupings in the southern half of Canada. (df = degree of freedom; RMSE = root mean square error).
Table 2. Regression models estimating in situ SDD from Landsat 8 Blue/Red surface reflectance for different ecozones or ecozone groupings in the southern half of Canada. (df = degree of freedom; RMSE = root mean square error).
EcozoneInterceptCoefficientdfRMSER2
Using 1-Day Window
Pacific Maritime and Montane Cordilleran0.6701.709353.230.477
Boreal Plain and Prairies0.3021.634431.120.523
Boreal Shield0.81691.0922031.700.263
Mixed Wood Plains0.6731.479541.440.549
Atlantic Maritime1.0070.879272.210.116
Using 7-Day Window
Pacific Maritime and Montane Cordilleran0.90331.34891443.070.402
Boreal Plain and Prairies0.25011.59992430.930.420
Boreal Shield0.87340.94367611.710.200
Mixed Wood Plains0.76121.32582481.370.444
Atlantic Maritime0.67221.57961091.720.384
Table
Table 3. Expanded regression models estimating in situ SDD from Landsat 8 Blue/Red surface reflectance using additional terms or different order polynomial models. Models use data for the seven-day temporal window between date of in situ sample and date of satellite overpass. (df = degree of freedom; RMSE = root mean square error).
Table 3. Expanded regression models estimating in situ SDD from Landsat 8 Blue/Red surface reflectance using additional terms or different order polynomial models. Models use data for the seven-day temporal window between date of in situ sample and date of satellite overpass. (df = degree of freedom; RMSE = root mean square error).
Equation FormdfBIASRMSER2Adjusted R2
Ln(SDD) = Ln(Blue/Red) 15110.3611.870.4670.467
Ln(SDD) = Ln(Blue/Red) + Blue15100.3541.870.4770.477
Ln(SDD) = Ln(Blue/Red) + Green15100.3491.850.5050.504
Ln(SDD) = Ln(Blue/Red) + Red15100.3571.860.4870.486
Ln(SDD) = Ln(Blue/Red) + NIR15100.3621.860.4680.468
Ln(SDD) = Ln(Blue/Red) + (Ln(Blue/Red))215100.3871.850.4780.470
Ln(SDD) = Ln(Blue/Red) + (Ln(Blue/Red))2 + (Ln(Blue/Red))315090.3861.850.4780.477
Ln(SDD) = Ln(Blue/Red) + (Ln(Blue/Red))2 + (Ln(Blue/Red))3 + (Ln(Blue/Red))415080.3871.850.4790.478
Table
Table 4. Regression models estimating in situ SDD from Landsat 8 Blue/Red surface reflectance for different temporal windows. (RMSE = root mean square error).
Table 4. Regression models estimating in situ SDD from Landsat 8 Blue/Red surface reflectance for different temporal windows. (RMSE = root mean square error).
Temporal WindowSample SizeInterceptCoefficientRMSEBiasR2Cross-Validated R2
Same Day4030.68341.43202.650.4130.4210.420
Median of Same Week15130.58771.56201.870.3610.4670.465
Median of Same Month21390.52371.72051.800.3190.5090.508
Median of Same Year18790.55001.70401.650.2870.5120.511
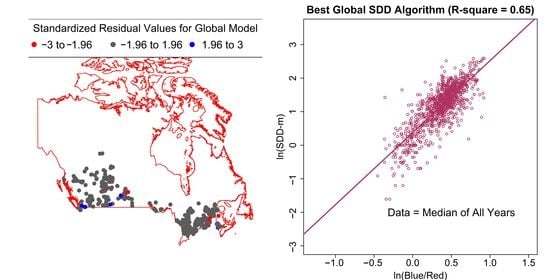
Median of All Years9770.37292.14521.750.2610.6450.643
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Deutsch, E.S.; Cardille, J.A.; Koll-Egyed, T.; Fortin, M.-J. Landsat 8 Lake Water Clarity Empirical Algorithms: Large-Scale Calibration and Validation Using Government and Citizen Science Data from across Canada. Remote Sens. 2021, 13, 1257. https://doi.org/10.3390/rs13071257

AMA Style

Deutsch ES, Cardille JA, Koll-Egyed T, Fortin M-J. Landsat 8 Lake Water Clarity Empirical Algorithms: Large-Scale Calibration and Validation Using Government and Citizen Science Data from across Canada. Remote Sensing. 2021; 13(7):1257. https://doi.org/10.3390/rs13071257

Chicago/Turabian Style

Deutsch, Eliza S., Jeffrey A. Cardille, Talia Koll-Egyed, and Marie-Josée Fortin. 2021. "Landsat 8 Lake Water Clarity Empirical Algorithms: Large-Scale Calibration and Validation Using Government and Citizen Science Data from across Canada" Remote Sensing 13, no. 7: 1257. https://doi.org/10.3390/rs13071257

APA Style

Deutsch, E. S., Cardille, J. A., Koll-Egyed, T., & Fortin, M. -J. (2021). Landsat 8 Lake Water Clarity Empirical Algorithms: Large-Scale Calibration and Validation Using Government and Citizen Science Data from across Canada. Remote Sensing, 13(7), 1257. https://doi.org/10.3390/rs13071257

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop