Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status
Abstract
:1. Introduction
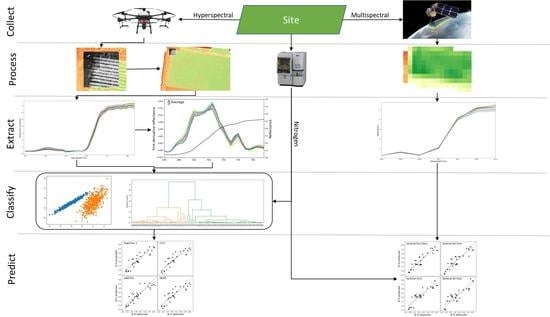
2. Materials and Methods
2.1. Study Site
2.2. Field Sampling
2.3. Hyperspectral Data Collection
2.4. Hyperspectral Derivatives Extraction
2.5. Machine Learning Classification on the Hyperspectral Datacube
2.6. Common Vegetation Indices Calculation
2.7. Sentinel 2 Data Extraction
2.8. Analysis of Nitrogen Prediction
3. Results
3.1. Hyperspectral Reflectance
3.2. Vegetation Indices
3.3. Machine Learning of Hyperspectral Reflectance for Optimised N Prediction
3.4. Novel Hyperspectral Vegetation Indices
3.5. Sentinel Reflectance
4. Discussion
4.1. Hyperspectral Performance
4.2. Machine Learning Impact
4.3. Sentinel Performance
5. Conclusions
- The hyperspectral datacube reported in this study was able to predict N levels across the site with high accuracy, both from simpler conventional VIs as well as machine learning derived VIs. The crop features were clearly discernible at plot, row, and down to plant scale.
- A machine learning approach narrows the optimisation search window making new spectral features easier and quicker to find and test.
- Sentinel data proved capable with these field samples to delineate N levels at coarse, production scale, though the sample locations compared to pixel boundaries suggest further comparison is needed.
- There were challenges with this study that could be addressed with further research. While the stitching artefacts had no impact on the sampled reflectance due to the field sample location being distant from the area involved, the stitching does impact the ability to visually infer N levels from that part of the field.
- The high-resolution continuous spectra argue for hyperspectral remote sensing’s ability to identify inter-plot as well as intra-plot variability, providing strong insight for development and refinement of a precision agriculture strategy while UAV platforms demonstrate high spatial resolution and responsiveness to producers or researchers needs. The machine learning derived VIs need further testing to ensure this performance holds across multiple seasons, sites and crops.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raper, T.B.; Varco, J.J. Canopy-scale wavelength and vegetative index sensitivities to cotton growth parameters and nitrogen status. Precis. Agric. 2014, 16, 62–76. [Google Scholar] [CrossRef] [Green Version]
- Rosolem, C.; Mikkelsen, D. Nitrogen source-sink relationship in cotton. J. Plant Nutr. 1989, 12, 1417–1433. [Google Scholar] [CrossRef]
- Yang, G.; Tang, H.; Nie, Y.; Zhang, X. Responses of cotton growth, yield, and biomass to nitrogen split application ratio. Eur. J. Agron. 2011, 35, 164–170. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Wang, Z.; Sun, H.; Zhang, Y.; Bai, Z.; Song, S.; Lu, Z.; Li, C. Nitrogen Fertilization Effects on Physiology of the Cotton Boll–Leaf System. Agronomy 2019, 9, 271. [Google Scholar] [CrossRef] [Green Version]
- Diaz, R.J.; Rosenberg, R. Spreading Dead Zones and Consequences for Marine Ecosystems. Science 2008, 321, 926–929. [Google Scholar] [CrossRef] [PubMed]
- Padilla, F.M.; Gallardo, M.; Manzano-Agugliaro, F. Global trends in nitrate leaching research in the 1960–2017 period. Sci. Total Environ. 2018, 643, 400–413. [Google Scholar] [CrossRef]
- Blesh, J.; Drinkwater, L.E. The impact of nitrogen source and crop rotation on nitrogen mass balances in the Mississippi River Basin. Ecol. Appl. 2013, 23, 1017–1035. [Google Scholar] [CrossRef]
- Macdonald, B.C.T.; Latimer, J.O.; Schwenke, G.D.; Nachimuthu, G.; Baird, J.C. The current status of nitrogen fertiliser use efficiency and future research directions for the Australian cotton industry. J. Cotton Res. 2018, 1, 15. [Google Scholar] [CrossRef]
- Ju, C.-H.; Tian, Y.-C.; Yao, X.; Cao, W.-X.; Zhu, Y.; Hannaway, D. Estimating Leaf Chlorophyll Content Using Red Edge Parameters. Pedosphere 2010, 20, 633–644. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; De Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Feng, W.; Guo, B.-B.; Wang, Z.-J.; He, L.; Song, X.; Wang, Y.-H.; Guo, T.-C. Measuring leaf nitrogen concentration in winter wheat using double-peak spectral reflection remote sensing data. Field Crop. Res. 2014, 159, 43–52. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Boochs, F.; Kupfer, G.; Dockter, K.; Kühbauch, W. Shape of the red edge as vitality indicator for plants. Int. J. Remote Sens. 1990, 11, 1741–1753. [Google Scholar] [CrossRef]
- Frazier, A.E.; Wang, L.; Chen, J. Two new hyperspectral indices for comparing vegetation chlorophyll content. Geo-Spat. Inf. Sci. 2014, 17, 17–25. [Google Scholar] [CrossRef]
- García-Berná, J.A.; Ouhbi, S.; Benmouna, B.; García-Mateos, G.; Fernández-Alemán, J.L.; Molina-Martínez, J.M. Systematic mapping study on remote sensing in agriculture. Appl. Sci. 2020, 10, 3456. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Nicodemus, F.E. Earrtum: Directional Reflectance and Emissivity of an Opaque Surface. Appl. Opt. 1966, 5, 715. [Google Scholar] [CrossRef]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective; Prentice Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Aasen, H.; Bolten, A. Multi-temporal high-resolution imaging spectroscopy with hyperspectral 2D imagers—From theory to application. Remote Sens. Environ. 2018, 205, 374–389. [Google Scholar] [CrossRef]
- Boggs, J.L.; Tsegaye, T.D.; Coleman, T.L.; Reddy, K.C.; Fahsi, A. Relationship between Hyperspectral Reflectance, Soil Nitrate-Nitrogen, Cotton Leaf Chlorophyll, and Cotton Yield: A Step toward Precision Agriculture. J. Sustain. Agric. 2003, 22, 5–16. [Google Scholar] [CrossRef]
- Zhao, D.; Reddy, K.R.; Kakani, V.G.; Read, J.J.; Koti, S. Selection of Optimum Reflectance Ratios for Estimating Leaf Nitrogen and Chlorophyll Concentrations of Field-Grown Cotton. Agron. J. 2005, 97, 89–98. [Google Scholar] [CrossRef] [Green Version]
- Buscaglia, H.J.; Varco, J.J. Early Detection of Cotton Leaf Nitrogen Status Using Leaf Reflectance. J. Plant Nutr. 2002, 25, 2067. [Google Scholar] [CrossRef]
- Hunt, R.E., Jr.; Cavigelli, M.; Daughtry, C.S.T.; McMurtrey, J.E.; Walthall, C.L. Evaluation of Digital Photography from Model Aircraft for Remote Sensing of Crop Biomass and Nitrogen Status. Precis. Agric. 2005, 6, 359–378. [Google Scholar] [CrossRef]
- Tarpley, L.; Reddy, K.R.; Sassenrath-Cole, G.F. Reflectance indices with precision and accuracy in predicting cotton leaf nitrogen concentration. Crop. Sci. 2000, 40, 1814–1819. [Google Scholar] [CrossRef]
- Feng, A.; Zhou, J.; Vories, E.; Sudduth, K.A. Evaluation of cotton emergence using UAV-based imagery and deep learning. Comput. Electron. Agric. 2020, 177, 105711. [Google Scholar] [CrossRef]
- Chen, R.; Chu, T.; Landivar, J.A.; Yang, C.; Maeda, M.M. Monitoring cotton (Gossypium hirsutum L.) germination using ultrahigh-resolution UAS images. Precis. Agric. 2018, 19, 161–177. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Bradford, J.M.; Murden, D. Airborne Hyperspectral Imagery and Yield Monitor Data for Mapping Cotton Yield Variability. Precis. Agric. 2004, 5, 445–461. [Google Scholar] [CrossRef]
- Filippi, P.; Whelan, B.M.; Vervoort, R.W.; Bishop, T.F. Mid-season empirical cotton yield forecasts at fine resolutions using large yield mapping datasets and diverse spatial covariates. Agric. Syst. 2020, 184, 102894. [Google Scholar] [CrossRef]
- Reisig, D.D.; Godfrey, L.D. Remotely Sensing Arthropod and Nutrient Stressed Plants: A Case Study With Nitrogen and Cotton Aphid (Hemiptera: Aphididae). Environ. Entomol. 2010, 39, 1255–1263. [Google Scholar] [CrossRef] [Green Version]
- Lowe, A.; Harrison, N.; French, A.P. Hyperspectral image analysis techniques for the detection and classification of the early onset of plant disease and stress. Plant Methods 2017, 13, 1–12. [Google Scholar] [CrossRef]
- Zhu, L.; Suomalainen, J.; Liu, J.; Hyyppä, J.; Kaartinen, H.; Haggren, H. A Review: Remote Sensing Sensors. Multi-Purp. Appl. Geospat. Data 2018. [Google Scholar] [CrossRef] [Green Version]
- Rouse, J.W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; SienceOpen: Burlington, MA, USA, 1973. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident detection of crop water stress, nitrogen status and canopy density using ground based multispectral data. In Proceedings of the Fifth International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Fridgen, J.L.; Varco, J.J. Dependency of Cotton Leaf Nitrogen, Chlorophyll, and Reflectance on Nitrogen and Potassium Availability. Agron. J. 2004, 96, 63–69. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Dufrêne, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Miller, J.R.; Hare, E.W.; Wu, J. Quantitative characterization of the vegetation red edge reflectance an inverted-Gaussian reflectance model. Int. J. Remote Sens. 1990, 11, 1755–1773. [Google Scholar] [CrossRef]
- Bonham-Carter, G. Numerical procedures and computer program for fitting an inverted gaussian model to vegetation reflectance data. Comput. Geosci. 1988, 14, 339–356. [Google Scholar] [CrossRef]
- Kochubey, S.M.; Kazantsev, T.A. Derivative vegetation indices as a new approach in remote sensing of vegetation. Front. Earth Sci. 2012, 6, 188–195. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Söderström, M.; Piikki, K.; Stenberg, M.; Stadig, H.; Martinsson, J. Producing nitrogen (N) uptake maps in winter wheat by combining proximal crop measurements with Sentinel-2 and DMC satellite images in a decision support system for farmers. Acta Agric. Scand. Sect. B 2017, 67, 637–650. [Google Scholar] [CrossRef]
- Laurent, V.C.; Schaepman, M.E.; Verhoef, W.; Weyermann, J.; Chávez, R.O. Bayesian object-based estimation of LAI and chlorophyll from a simulated Sentinel-2 top-of-atmosphere radiance image. Remote Sens. Environ. 2014, 140, 318–329. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Rivera, J.P.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model. Remote Sens. 2013, 5, 3280–3304. [Google Scholar] [CrossRef] [Green Version]
- Habyarimana, E.; Piccard, I.; Catellani, M.; De Franceschi, P.; Dall’Agata, M. Towards Predictive Modeling of Sorghum Biomass Yields Using Fraction of Absorbed Photosynthetically Active Radiation Derived from Sentinel-2 Satellite Imagery and Supervised Machine Learning Techniques. Agronomy 2019, 9, 203. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Wang, J. Mapping Winter Wheat Planting Area and Monitoring Its Phenology Using Sentinel-1 Backscatter Time Series. Remote Sens. 2019, 11, 449. [Google Scholar] [CrossRef] [Green Version]
- Meier, J.; Mauser, W.; Hank, T.; Bach, H. Assessments on the impact of high-resolution-sensor pixel sizes for common agricultural policy and smart farming services in European regions. Comput. Electron. Agric. 2020, 169, 105205. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Yamaguchi, T.; Tanaka, Y.; Imachi, Y.; Yamashita, M.; Katsura, K. Feasibility of Combining Deep Learning and RGB Images Obtained by Unmanned Aerial Vehicle for Leaf Area Index Estimation in Rice. Remote Sens. 2020, 13, 84. [Google Scholar] [CrossRef]
- Zhao, W.; Yamada, W.; Li, T.; Digman, M.; Runge, T. Augmenting Crop Detection for Precision Agriculture with Deep Visual Transfer Learning—A Case Study of Bale Detection. Remote Sens. 2020, 13, 23. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Linna, P.; Lipping, T. Crop Yield Prediction Using Multitemporal UAV Data and Spatio-Temporal Deep Learning Models. Remote Sens. 2020, 12, 4000. [Google Scholar] [CrossRef]
- Féret, J.-B.; le Maire, G.; Jay, S.; Berveiller, D.; Bendoula, R.; Hmimina, G.; Cheraiet, A.; Oliveira, J.; Ponzoni, F.; Solanki, T.; et al. Estimating leaf mass per area and equivalent water thickness based on leaf optical properties: Potential and limitations of physical modeling and machine learning. Remote Sens. Environ. 2019, 231, 110959. [Google Scholar] [CrossRef]
- Hulugalle, N.R.; Weaver, T.B.; Finlay, L.A.; Lonergan, P. Soil properties, black root-rot incidence, yield, and greenhouse gas emissions in irrigated cotton cropping systems sown in a Vertosol with subsoil sodicity. Soil Res. 2012, 50, 278–292. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Louhichi, S.; Gzara, M.; Ben Abdallah, H. A density based algorithm for discovering clusters with varied density. In Proceedings of the 2014 World Congress on Computer Applications and Information Systems (WCCAIS), Hammamet, Tunisia, 17–19 January 2014; pp. 1–6. [Google Scholar]
- Rokach, L. A survey of Clustering Algorithms. In Data Mining and Knowledge Discovery Handbook; Springer International Publishing: Berlin/Heidelberg, Germany, 2009; pp. 269–298. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]













| Name | Equation | Source |
|---|---|---|
| NDVI | [36] | |
| NDRE | [37] | |
| VOG1 | [38] | |
| CCCI | [39] | |
| [40] | ||
| mND705 | [19] | |
| NDDAmid | [13] | |
| DIDAmid | [13] | |
| RIDAmid | [13] | |
| LSDRmid | [13] | |
| RSDRmid | [13] |
| VI | RMSE | R2 | LCC | Equation |
|---|---|---|---|---|
| RIDAmid | 0.210 | 0.813 | 0.898 | y = 1.491x − 0.065 |
| VOG1 | 0.214 | 0.806 | 0.894 | y = 4.71x − 6.161 |
| DIDAmid | 0.222 | 0.791 | 0.885 | y = 54.436x + 0.682 |
| CCCI | 0.222 | 0.789 | 0.884 | y = 12.683x − 3.6 |
| mND705 | 0.223 | 0.788 | 0.884 | y = 15.827x − 9.577 |
| NDDAmid | 0.226 | 0.783 | 0.880 | y = 7.072x + 0.598 |
| NDRE | 0.227 | 0.780 | 0.878 | y = 12.856x − 2.935 |
| RSDRmid | 0.273 | 0.682 | 0.815 | y = 84.685x − 4.091 |
| LSDRmid | 0.282 | 0.662 | 0.800 | y = −106.438x + 7.413 |
| 0.292 | 0.636 | 0.786 | y = 1.511x + 6.171 | |
| NDVI | 0.325 | 0.550 | 0.720 | y = 56.311x − 46.92 |
| Band | GSD (m) | RMSE | R2 | LCC | Equation |
|---|---|---|---|---|---|
| Green (B3 543–578 nm) | 10 | 0.187 | 0.852 | 0.921 | y = −163.972 x + 13.22 |
| Green (B3 543–578 nm) | 5 | 0.204 | 0.823 | 0.904 | y = −161.298x + 13.001 |
| CCCI | 5 | 0.208 | 0.816 | 0.900 | y = 29.96x − 19.133 |
| REP1 (B5 698–713 nm) | 5 | 0.225 | 0.785 | 0.882 | y = −114.364x + 15.364 |
| 5 | 0.236 | 0.762 | 0.868 | y = −44.607x + 10.538 | |
| mND705 | 5 | 0.242 | 0.750 | 0.861 | y = 27.209x − 14.748 |
| NDRE | 5 | 0.243 | 0.748 | 0.860 | y = 23.798x − 12.602 |
| VOG1 | 5 | 0.260 | 0.713 | 0.838 | y = 2.516x − 6.481 |
| REP1 (B5 698–713 nm) | 20 | 0.271 | 0.688 | 0.818 | y = −110.096x + 14.984 |
| NIR (B8 785–899 nm) | 5 | 0.355 | 0.462 | 0.642 | y = 19.512 − 7.12 |
| REP3 (B7 773–793 nm) | 5 | 0.391 | 0.348 | 0.536 | y = 22.854 − 8.588 |
| NDVI | 5 | 0.395 | 0.337 | 0.531 | y = 36.428x − 29.282 |
| Red (B4 650–680 nm) | 5 | 0.442 | 0.169 | 0.328 | y = −152.78x + 7.798 |
| REP2 (B6 733–748 nm) | 5 | 0.486 | 0.000 | 0.085 | y = 22.348 − 6.007 |
| Blue (B2 458–523 nm) | 5 | 0.488 | 0.000 | 0.064 | y = −314.119x + 12.034 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marang, I.J.; Filippi, P.; Weaver, T.B.; Evans, B.J.; Whelan, B.M.; Bishop, T.F.A.; Murad, M.O.F.; Al-Shammari, D.; Roth, G. Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status. Remote Sens. 2021, 13, 1428. https://doi.org/10.3390/rs13081428
Marang IJ, Filippi P, Weaver TB, Evans BJ, Whelan BM, Bishop TFA, Murad MOF, Al-Shammari D, Roth G. Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status. Remote Sensing. 2021; 13(8):1428. https://doi.org/10.3390/rs13081428
Chicago/Turabian StyleMarang, Ian J., Patrick Filippi, Tim B. Weaver, Bradley J. Evans, Brett M. Whelan, Thomas F. A. Bishop, Mohammed O. F. Murad, Dhahi Al-Shammari, and Guy Roth. 2021. "Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status" Remote Sensing 13, no. 8: 1428. https://doi.org/10.3390/rs13081428
APA StyleMarang, I. J., Filippi, P., Weaver, T. B., Evans, B. J., Whelan, B. M., Bishop, T. F. A., Murad, M. O. F., Al-Shammari, D., & Roth, G. (2021). Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status. Remote Sensing, 13(8), 1428. https://doi.org/10.3390/rs13081428