Figure 1.
Results of the simulation data with 3 bands. (a): the distribution of the simulation image in 2-dimensional spectral space (Band 1 and 2), where the background pixels satisfy an 2-dimensional normal distribution. Moreover, the target vector is set to: (the upper left region in (c)), (the lower right region in (c)); (b): the distribution of the simulation image in 3-dimensional spectral space, where Band 3 is a noisy one. (c): the groundtruth image for the target of interest; (d): the CEM result using full bands (); (e): the CEM result using Band 1 and 2 (), where the first pixel of the target image at the upper left corner is selected as the representative spectrum of the target.
Figure 1.
Results of the simulation data with 3 bands. (a): the distribution of the simulation image in 2-dimensional spectral space (Band 1 and 2), where the background pixels satisfy an 2-dimensional normal distribution. Moreover, the target vector is set to: (the upper left region in (c)), (the lower right region in (c)); (b): the distribution of the simulation image in 3-dimensional spectral space, where Band 3 is a noisy one. (c): the groundtruth image for the target of interest; (d): the CEM result using full bands (); (e): the CEM result using Band 1 and 2 (), where the first pixel of the target image at the upper left corner is selected as the representative spectrum of the target.
Figure 2.
The false color image (a) (R:750.6 nm, G:559.6 nm, B: 510.1 nm) and the groundtruth image (b) for the Xi’an data with 64 bands. (c) The selected spectrum of the target of interest.
Figure 2.
The false color image (a) (R:750.6 nm, G:559.6 nm, B: 510.1 nm) and the groundtruth image (b) for the Xi’an data with 64 bands. (c) The selected spectrum of the target of interest.
Figure 3.
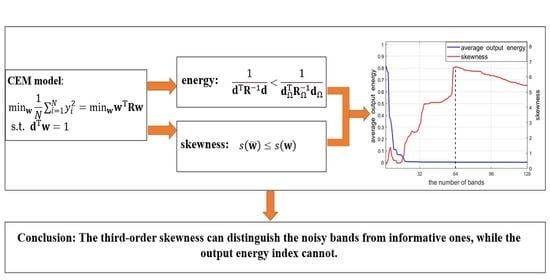
For the Xi’an data with 64 bands, the average output energy and the skewness curves as a function of L, ranging from 2 to 128, where the last 64 bands are noisy ones. (The black vertical dotted line corresponds to the data with full bands (), after which the noisy bands with Gaussian distribution are added. It can be seen that the skewness value at is the maximum).
Figure 3.
For the Xi’an data with 64 bands, the average output energy and the skewness curves as a function of L, ranging from 2 to 128, where the last 64 bands are noisy ones. (The black vertical dotted line corresponds to the data with full bands (), after which the noisy bands with Gaussian distribution are added. It can be seen that the skewness value at is the maximum).
Figure 4.
For the Xi’an data with 64 bands, (a): the correlation coefficient image between all bands with a size of (a larger value indicates a higher correlation); (b): the correlation coefficient image of Band 1–10; (c): the correlation coefficient image of Band 25–34; (d–h): the gray image for Band 6–8, 26-27. The corresponding correlation coefficient between Band i and j (denoted ) are attached: , , , .
Figure 4.
For the Xi’an data with 64 bands, (a): the correlation coefficient image between all bands with a size of (a larger value indicates a higher correlation); (b): the correlation coefficient image of Band 1–10; (c): the correlation coefficient image of Band 25–34; (d–h): the gray image for Band 6–8, 26-27. The corresponding correlation coefficient between Band i and j (denoted ) are attached: , , , .
Figure 5.
For the Xi’an data with 64 bands, (a–e) the CEM results for different numbers of bands, where ; (f) the CEM result with the skewness selection process, and ; (g): the ROC curves for the CEM results with different Ls.
Figure 5.
For the Xi’an data with 64 bands, (a–e) the CEM results for different numbers of bands, where ; (f) the CEM result with the skewness selection process, and ; (g): the ROC curves for the CEM results with different Ls.
Figure 6.
For the YC lake data with 150 bands, (a): the false color image (R: 860.88 nm, G: 651.31 nm, B: 548.66 nm); (b): the groundtruth image; (c): the selected spectrum of the target of interest; (d): the skewness curve as a function of L, ranging from 2 to 150.
Figure 6.
For the YC lake data with 150 bands, (a): the false color image (R: 860.88 nm, G: 651.31 nm, B: 548.66 nm); (b): the groundtruth image; (c): the selected spectrum of the target of interest; (d): the skewness curve as a function of L, ranging from 2 to 150.
Figure 7.
For the YC Lake data with 150 bands, (a): the correlation coefficient image between the spectral bands with a size of ; (b): the correlation coefficient image of Band 15–24; (c): the correlation coefficient image of Band 111–120; (d–i): the gray image for Band 19–21, 113–115. The corresponding correlation coefficient between Band i and j (denoted ) are attached: , , , , .
Figure 7.
For the YC Lake data with 150 bands, (a): the correlation coefficient image between the spectral bands with a size of ; (b): the correlation coefficient image of Band 15–24; (c): the correlation coefficient image of Band 111–120; (d–i): the gray image for Band 19–21, 113–115. The corresponding correlation coefficient between Band i and j (denoted ) are attached: , , , , .
Figure 8.
For the YC Lake data with 150 bands, (a–f): the CEM results for different Ls (L = 5, 10, 40, 50, 100, 150); (g): the CEM result with the skewness selection process, and ; (h): the ROC curves with different Ls.
Figure 8.
For the YC Lake data with 150 bands, (a–f): the CEM results for different Ls (L = 5, 10, 40, 50, 100, 150); (g): the CEM result with the skewness selection process, and ; (h): the ROC curves with different Ls.
Figure 9.
For the Indian Pines data with 200 bands, (a) the false color image (R:Band 44, G:Band 31, B:Band 18); (b): groundtruth data with 16 classes; (c): the groundtruth image for the 16th class; (d): the selected spectrum of the target.
Figure 9.
For the Indian Pines data with 200 bands, (a) the false color image (R:Band 44, G:Band 31, B:Band 18); (b): groundtruth data with 16 classes; (c): the groundtruth image for the 16th class; (d): the selected spectrum of the target.
Figure 10.
For the Indian Pines data, (a): the CEM result with 25 bands via down-sampling by averaging the data with 200 bands; (b): the CEM result with 400 bands generated by GCEM; (c): the CEM result for the data with the skewness selection process, and ; (d): the ROC curves with different Ls.
Figure 10.
For the Indian Pines data, (a): the CEM result with 25 bands via down-sampling by averaging the data with 200 bands; (b): the CEM result with 400 bands generated by GCEM; (c): the CEM result for the data with the skewness selection process, and ; (d): the ROC curves with different Ls.
Table 1.
For the simulation data with 3 bands, the comparison of the average filter output energy and the absolute value of the skewness using different Ls.
Table 1.
For the simulation data with 3 bands, the comparison of the average filter output energy and the absolute value of the skewness using different Ls.
| Band Number | | |
|---|
| Energy | 0.2048 | 0.1228 |
| Skewness | 1.3956 | 0.6810 |
Table 2.
Illustration of the confusion matrix of a binary classification.
Table 2.
Illustration of the confusion matrix of a binary classification.
| | Target | Non-Target |
|---|
| Hypothesized Target | True positive (TP) | False positive (FP) |
| Hypothesized Non-target | False negative (FN) | True negative (TN) |
Table 3.
The quantitative comparison for AUC, OA, F-score (denoted ), and Kappa coefficient (denoted ) with different Ls for the Xi’an data. Bold numbers indicate the highest values in each row.
Table 3.
The quantitative comparison for AUC, OA, F-score (denoted ), and Kappa coefficient (denoted ) with different Ls for the Xi’an data. Bold numbers indicate the highest values in each row.
| L | 4 | 8 | 16 | 32 | 64 | 45 |
|---|
| 0.8300 | 0.9429 | 0.9407 | 0.9422 | 0.9503 | 0.9557 |
| 0.7849 | 0.8905 | 0.8757 | 0.8816 | 0.9191 | 0.9253 |
| 0.7679 | 0.8850 | 0.8737 | 0.8788 | 0.9148 | 0.9231 |
| 0.5697 | 0.7809 | 0.7513 | 0.7632 | 0.8382 | 0.8507 |
Table 4.
The quantitative comparison for AUC, OA, F-score (denoted ), and Kappa coefficient (denoted ) with different Ls for the YC Lake data. Bold numbers indicate the highest values in each row.
Table 4.
The quantitative comparison for AUC, OA, F-score (denoted ), and Kappa coefficient (denoted ) with different Ls for the YC Lake data. Bold numbers indicate the highest values in each row.
| L | 5 | 10 | 30 | 50 | 75 | 150 | 83 |
|---|
| 0.9628 | 0.9654 | 0.9790 | 0.9799 | 0.9834 | 0.9811 | 0.9844 |
| 0.9066 | 0.9103 | 0.9353 | 0.9355 | 0.9401 | 0.9361 | 0.9416 |
| 0.9074 | 0.9105 | 0.9353 | 0.9354 | 0.9398 | 0.9358 | 0.9416 |
| 0.8133 | 0.8206 | 0.8707 | 0.8710 | 0.8802 | 0.8722 | 0.8831 |
Table 5.
The classes’ names and the number of sample for the Indian Pine data.
Table 5.
The classes’ names and the number of sample for the Indian Pine data.
| No. | Class | Samples |
|---|
| 1 | Alfalfa | 46 |
| 2 | Corn-notill | 1428 |
| 3 | Corn-mintill | 830 |
| 4 | Corn | 237 |
| 5 | Grass-pasture | 483 |
| 6 | Grass-trees | 730 |
| 7 | Grass-pasture-mowed | 28 |
| 8 | Hay-windrowed | 478 |
| 9 | Oats | 20 |
| 10 | Soybean-notill | 972 |
| 11 | Soybean-mintill | 2455 |
| 12 | Soybean-clean | 593 |
| 13 | Wheat | 205 |
| 14 | Woods | 1265 |
| 15 | Buildings-Grass-Trees-Drives | 386 |
| 16 | Stone-Steel-Towers | 93 |
| Total | | 10,249 |
Table 6.
The quantitative comparison for AUC, OA, F-score (denoted ), and Kappa coefficient (denoted ) with different Ls for the Indian Pine data. Bold numbers indicate the highest values in each row.
Table 6.
The quantitative comparison for AUC, OA, F-score (denoted ), and Kappa coefficient (denoted ) with different Ls for the Indian Pine data. Bold numbers indicate the highest values in each row.
| L | 25 | 400 | 193 |
|---|
| 0.9972 | 0.9611 | 0.9989 |
| 0.9755 | 0.9591 | 0.9863 |
| 0.9754 | 0.9582 | 0.9862 |
| 0.9511 | 0.9183 | 0.9726 |