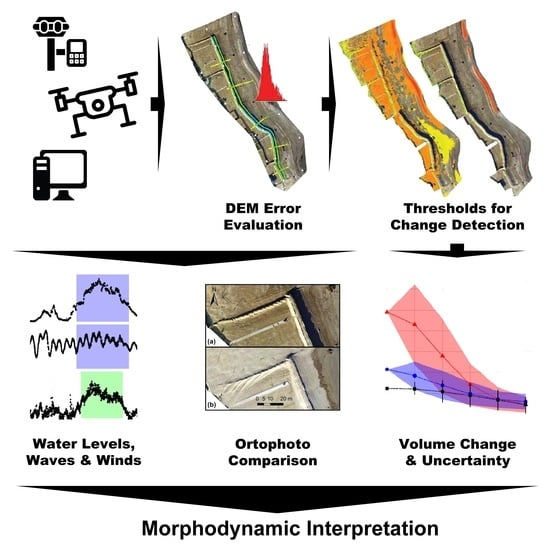
Uncertainty of Drone-Derived DEMs and Significance of Detected Morphodynamics in Artificially Scraped Dunes
Abstract
:1. Introduction
1.1. Artificial Dunes and Beach Scraping
1.2. Coastal Monitoring with Drones
1.3. Accounting for the Digital Elevation Model’s Uncertainties in Morphodynamic Assessments
1.4. Aim of the Paper
2. Case Study
2.1. Regional Context
2.2. Scraped Dunes at Porto Garibaldi
3. Methods and Data
3.1. Field Surveys
3.2. Photogrammetric Reconstruction
3.3. Digital Elevation Model Error Analysis
3.4. Significant Morphological Variations
3.5. Morphodynamic Drivers
3.5.1. Sea Forcing
3.5.2. Aeolian Forcing
4. Results
4.1. Digital Elevation Model Error Analysis



4.2. Significant Morphological Variations
4.3. Morphodynamic Drivers
4.3.1. Sea Forcing
4.3.2. Aeolian Forcing
5. Discussion
5.1. DEM Errors and Significant Morphological Variations
5.2. Interpretation of the Morphological Variations
5.2.1. How Did the Sea Forcing Affect the Scraped Beach?
5.2.2. How Did the Aeolian Forcing Affect the Scraped Beach?
5.2.3. Are Aeolian-Driven Changes Less Significant Than Sea-Driven Ones?
5.2.4. What If the Beach Was Not Scraped?
5.3. Thresholds and Uncertainty in Morphodynamic Assessments
- The application of a set of uniform thresholds to detect significant changes, which allowed an understanding of the variability of the calculated volume changes and the associated uncertainty;
- The thorough assessment of the uncertainty generated by the propagation of the original uncertainty of the UAV-derived elevation products, which provided a reference to evaluate the appropriateness of the applied thresholds;
- The evaluation of the characteristics of the morphodynamic drivers by adopting uncertainty-aware approaches when possible.
- Estimating the optimal threshold as function of the propagated uncertainty of the input elevation data provides a reference value able to detect the main morphological localised variations, which, in the case of coastal areas, are generally associated with erosion due to sea waves and water levels or aeolian deposition;
- The optimal threshold provides a first noise-filtered estimate of volume variations (and associated uncertainty) but it masks the contribution of subtle variations that are incorrectly filtered out due to their magnitude being comparable with the instrumental accuracy and/or the assessed propagated DoD uncertainty;
- Applying lower thresholds than the optimal one increases the uncertainty of the volume change assessments, but helps in identifying subtle spread variations, which, in the case of coastal areas, are generally associated with aeolian erosion, or waves and water level deposition;
- The lower thresholds provide largely uncertain estimates of volume change that must be carefully considered and interpreted with the support of all the available information (forcing, orthophotos, etc.).
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bruun, P. Beach Scraping—Is It Damaging to Beach Stability? Coast. Eng. 1983, 7, 167–173. [Google Scholar] [CrossRef]
- Harley, M.D.; Ciavola, P. Managing Local Coastal Inundation Risk Using Real-Time Forecasts and Artificial Dune Placements. Coast. Eng. 2013, 77, 77–90. [Google Scholar] [CrossRef]
- Wells, J.T.; McNinch, J. Beach Scraping in North Carolina with Special Reference to Its Effectiveness During Hurricane Hugo. J. Coast. Res. 1991, 8, 249–261. [Google Scholar]
- Cooke, B.C.; Jones, A.R.; Goodwin, I.D.; Bishop, M.J. Nourishment Practices on Australian Sandy Beaches: A Review. J. Environ. Manage. 2012, 113, 319–327. [Google Scholar] [CrossRef]
- Smyth, T.A.G.; Hesp, P.A. Aeolian Dynamics of Beach Scraped Ridge and Dyke Structures. Coast. Eng. 2015, 99, 38–45. [Google Scholar] [CrossRef] [Green Version]
- Ellis, J.T.; Román-Rivera, M.A. Assessing Natural and Mechanical Dune Performance in a Post-Hurricane Environment. J. Mar. Sci. Eng. 2019, 7, 126. [Google Scholar] [CrossRef] [Green Version]
- Kelley, J.T. Popham Beach, Maine: An Example of Engineering Activity That Saved Beach Property without Harming the Beach. Geomorphology 2013, 199, 171–178. [Google Scholar] [CrossRef]
- Harley, M.D.; Valentini, A.; Armaroli, C.; Perini, L.; Calabrese, L.; Ciavola, P. Can an Early-Warning System Help Minimize the Impacts of Coastal Storms? A Case Study of the 2012 Halloween Storm, Northern Italy. Nat. Hazards Earth Syst. Sci. 2016, 16, 209–222. [Google Scholar] [CrossRef] [Green Version]
- Scarelli, F.M.; Sistilli, F.; Fabbri, S.; Cantelli, L.; Barboza, E.G.; Gabbianelli, G. Seasonal Dune and Beach Monitoring Using Photogrammetry from UAV Surveys to Apply in the ICZM on the Ravenna Coast (Emilia-Romagna, Italy). Remote Sens. Appl. Soc. Environ. 2017, 7, 27–39. [Google Scholar] [CrossRef]
- Sanuy, M.; Duo, E.; Jäger, W.S.; Ciavola, P.; Jiménez, J.A. Linking Source with Consequences of Coastal Storm Impacts for Climate Change and Risk Reduction Scenarios for Mediterranean Sandy Beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 1825–1847. [Google Scholar] [CrossRef] [Green Version]
- Conaway, C.A.; Wells, J.T. Aeolian Dynamics along Scraped Shorelines, Bogue Banks, North Carolina. J. Coast. Res. 2005, 212, 242–254. [Google Scholar] [CrossRef]
- Chen, B.; Yang, Y.; Wen, H.; Ruan, H.; Zhou, Z.; Luo, K.; Zhong, F. High-Resolution Monitoring of Beach Topography and Its Change Using Unmanned Aerial Vehicle Imagery. Ocean Coast. Manag. 2018, 160, 103–116. [Google Scholar] [CrossRef]
- Derian, P.; Almar, R. Wavelet-Based Optical Flow Estimation of Instant Surface Currents From Shore-Based and UAV Videos. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5790–5797. [Google Scholar] [CrossRef]
- Duo, E.; Trembanis, A.C.; Dohner, S.; Grottoli, E.; Ciavola, P. Local-Scale Post-Event Assessments with GPS and UAV-Based Quick-Response Surveys: A Pilot Case from the Emilia–Romagna (Italy) Coast. Nat. Hazards Earth Syst. Sci. 2018, 18, 2969–2989. [Google Scholar] [CrossRef] [Green Version]
- Berni, J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and Narrowband Multispectral Remote Sensing for Vegetation Monitoring From an Unmanned Aerial Vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef] [Green Version]
- Gomes, I.; Peteiro, L.; Bueno-Pardo, J.; Albuquerque, R.; Pérez-Jorge, S.; Oliveira, E.R.; Alves, F.L.; Queiroga, H. What’s a Picture Really Worth? On the Use of Drone Aerial Imagery to Estimate Intertidal Rocky Shore Mussel Demographic Parameters. Estuar. Coast. Shelf Sci. 2018, 213, 185–198. [Google Scholar] [CrossRef]
- Gonçalves, G.; Andriolo, U.; Pinto, L.; Bessa, F. Mapping Marine Litter Using UAS on a Beach-Dune System: A Multidisciplinary Approach. Sci. Total Environ. 2020, 706, 135742. [Google Scholar] [CrossRef]
- Rivas-Torres, G.F.; Benítez, F.L.; Rueda, D.; Sevilla, C.; Mena, C.F. A Methodology for Mapping Native and Invasive Vegetation Coverage in Archipelagos: An Example from the Galápagos Islands. Prog. Phys. Geogr. Earth Environ. 2018, 42, 83–111. [Google Scholar] [CrossRef] [Green Version]
- Grottoli, E.; Biausque, M.; Rogers, D.; Jackson, D.W.T.; Cooper, J.A.G. Structure-from-Motion-Derived Digital Surface Models from Historical Aerial Photographs: A New 3D Application for Coastal Dune Monitoring. Remote Sens. 2021, 13, 95. [Google Scholar] [CrossRef]
- Casella, E.; Drechsel, J.; Winter, C.; Benninghoff, M.; Rovere, A. Accuracy of Sand Beach Topography Surveying by Drones and Photogrammetry. Geo-Mar. Lett. 2020, 40, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Turner, I.L.; Harley, M.D.; Drummond, C.D. UAVs for Coastal Surveying. Coast. Eng. 2016, 114, 19–24. [Google Scholar] [CrossRef]
- Dohner, S.M.; Trembanis, A.C.; Miller, D.C. A Tale of Three Storms: Morphologic Response of Broadkill Beach, Delaware, Following Superstorm Sandy, Hurricane Joaquin, and Winter Storm Jonas. Shore Beach 2016, 84, 3–9. [Google Scholar]
- Casella, E.; Rovere, A.; Pedroncini, A.; Mucerino, L.; Casella, M.; Cusati, L.A.; Vacchi, M.; Ferrari, M.; Firpo, M. Study of Wave Runup Using Numerical Models and Low-Altitude Aerial Photogrammetry: A Tool for Coastal Management. Estuar. Coast. Shelf Sci. 2014, 149, 160–167. [Google Scholar] [CrossRef]
- Casella, E.; Rovere, A.; Pedroncini, A.; Stark, C.P.; Casella, M.; Ferrari, M.; Firpo, M. Drones as Tools for Monitoring Beach Topography Changes in the Ligurian Sea (NW Mediterranean). Geo-Mar. Lett. 2016, 36, 151–163. [Google Scholar] [CrossRef]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using Unmanned Aerial Vehicles (UAV) for High-Resolution Reconstruction of Topography: The Structure from Motion Approach on Coastal Environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef] [Green Version]
- Seymour, A.C.; Ridge, J.T.; Rodriguez, A.B.; Newton, E.; Dale, J.; Johnston, D.W. Deploying Fixed Wing Unoccupied Aerial Systems (UAS) for Coastal Morphology Assessment and Management. J. Coast. Res. 2018, 34, 704. [Google Scholar] [CrossRef]
- Godfrey, S.; Cooper, J.; Bezombes, F.; Plater, A. Monitoring Coastal Morphology: The Potential of Low-cost Fixed Array Action Cameras for 3D Reconstruction. Earth Surf. Process. Landf. 2020, 45, 2478–2494. [Google Scholar] [CrossRef]
- Moloney, J.G.; Hilton, M.J.; Sirguey, P.; Simons-Smith, T. Coastal Dune Surveying Using a Low-Cost Remotely Piloted Aerial System (RPAS). J. Coast. Res. 2018, 345, 1244–1255. [Google Scholar] [CrossRef]
- Sherman, D.J. Understanding Wind-Blown Sand: Six Vexations. Geomorphology 2020, 366, 107193. [Google Scholar] [CrossRef]
- Li, Z. A Comparative Study of the Accuracy of Digital Terrain Models (DTMs) Based on Various Data Models. ISPRS J. Photogramm. Remote Sens. 1994, 49, 2–11. [Google Scholar] [CrossRef]
- Erdogan, S. A Comparision of Interpolation Methods for Producing Digital Elevation Models at the Field Scale. Earth Surf. Process. Landf. 2009, 34, 366–376. [Google Scholar] [CrossRef]
- Cowell, P.J.; Zeng, T.Q. Integrating Uncertainty Theories with GIS for Modeling Coastal Hazards of Climate Change. Mar. Geod. 2003, 26, 5–18. [Google Scholar] [CrossRef]
- Wechsler, S.P.; Kroll, C.N. Quantifying DEM Uncertainty and Its Effect on Topographic Parameters. Photogramm. Eng. Remote Sens. 2006, 72, 1081–1090. [Google Scholar] [CrossRef] [Green Version]
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for Uncertainty in DEMs from Repeat Topographic Surveys: Improved Sediment Budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Leon, J.X.; Heuvelink, G.B.M.; Phinn, S.R. Incorporating DEM Uncertainty in Coastal Inundation Mapping. PLoS ONE 2014, 9, e108727. [Google Scholar] [CrossRef]
- Passalacqua, P.; Belmont, P.; Staley, D.M.; Simley, J.D.; Arrowsmith, J.R.; Bode, C.A.; Crosby, C.; DeLong, S.B.; Glenn, N.F.; Kelly, S.A.; et al. Analyzing High Resolution Topography for Advancing the Understanding of Mass and Energy Transfer through Landscapes: A Review. Earth-Sci. Rev. 2015, 148, 174–193. [Google Scholar] [CrossRef] [Green Version]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997; ISBN 978-0-935702-42-2. [Google Scholar]
- Brasington, J.; Rumsby, B.T.; Mcvey, R.A. Monitoring and Modelling Morphological Change in a Braided Gravel-Bed River Using High Resolution GPS-Based Survey. Earth Surf. Process. Landf. 2000, 25, 973–990. [Google Scholar] [CrossRef]
- Brasington, J.; Langham, J.; Rumsby, B. Methodological Sensitivity of Morphometric Estimates of Coarse Fluvial Sediment Transport. Geomorphology 2003, 53, 299–316. [Google Scholar] [CrossRef]
- Lane, S.N.; Westaway, R.M.; Murray Hicks, D. Estimation of Erosion and Deposition Volumes in a Large, Gravel-Bed, Braided River Using Synoptic Remote Sensing. Earth Surf. Process. Landf. 2003, 28, 249–271. [Google Scholar] [CrossRef]
- Neverman, A.J.; Fuller, I.C.; Procter, J.N. Application of Geomorphic Change Detection (GCD) to Quantify Morphological Budgeting Error in a New Zealand Gravel-Bed River: A Case Study from the Makaroro River, Hawke’s Bay. J. Hydrol. N. Z. 2016, 55, 45–63. [Google Scholar]
- Brunetta, R.; de Paiva, J.S.; Ciavola, P. Morphological Evolution of an Intertidal Area Following a Set-Back Scheme: A Case Study From the Perkpolder Basin (Netherlands). Front. Earth Sci. 2019, 7, 228. [Google Scholar] [CrossRef]
- Le Mauff, B.; Juigner, M.; Ba, A.; Robin, M.; Launeau, P.; Fattal, P. Coastal Monitoring Solutions of the Geomorphological Response of Beach-Dune Systems Using Multi-Temporal LiDAR Datasets (Vendée Coast, France). Geomorphology 2018, 304, 121–140. [Google Scholar] [CrossRef]
- Fryirs, K.A.; Wheaton, J.M.; Bizzi, S.; Williams, R.; Brierley, G.J. To Plug-in or Not to Plug-in? Geomorphic Analysis of Rivers Using the River Styles Framework in an Era of Big Data Acquisition and Automation. Wiley Interdiscip. Rev. Water 2019, 6, e1372. [Google Scholar] [CrossRef]
- Armaroli, C.; Ciavola, P.; Perini, L.; Calabrese, L.; Lorito, S.; Valentini, A.; Masina, M. Critical Storm Thresholds for Significant Morphological Changes and Damage along the Emilia-Romagna Coastline, Italy. Geomorphology 2012, 143, 34–51. [Google Scholar] [CrossRef]
- Armaroli, C.; Duo, E. Validation of the Coastal Storm Risk Assessment Framework along the Emilia-Romagna Coast. Coast. Eng. 2018, 134, 159–167. [Google Scholar] [CrossRef] [Green Version]
- Perini, L.; Calabrese, L.; Salerno, G.; Ciavola, P.; Armaroli, C. Evaluation of Coastal Vulnerability to Flooding: Comparison of Two Different Methodologies Adopted by the Emilia-Romagna Region (Italy). Nat. Hazards Earth Syst. Sci. 2016, 16, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Regione Emilia-Romagna Strategie e Strumenti di Gestione della Costa in Emilia-Romagna; Servizio Difesa del Suolo, della Costa e Bonifica-Regione Emilia-Romagna: Bologna, Italy, 2011.
- MATTM-Regioni. Linee Guida per La Difesa Della Costa Dai Fenomeni Di Erosione e Dagli Effetti Dei Cambiamenti Climatici. Versione 2018-Documento Elaborato Dal Tavolo Nazionale Sull’Erosione Costiera MATTM-Regioni Con Il Coordinamento Tecnico Di ISPRA; MATTM-Regioni: Rome, Italy, 2018; p. 305. [Google Scholar]
- Garnier, E.; Ciavola, P.; Spencer, T.; Ferreira, O.; Armaroli, C.; McIvor, A. Historical Analysis of Storm Events: Case Studies in France, England, Portugal and Italy. Coast. Eng. 2018, 134, 10–23. [Google Scholar] [CrossRef] [Green Version]
- Perini, L.; Calabrese, L.; Lorito, S.; Luciani, P. Costal Flood Risk in Emilia-Romagna (Italy): The Sea Storm of February 2015. In Proceedings of the Coastal and Maritime Mediterranean Conference Edition 3, Ferrara, Italy, 25–27 November 2015; pp. 225–230. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- James, M.R.; Robson, S.; Smith, M.W. 3-D Uncertainty-Based Topographic Change Detection with Structure-from-Motion Photogrammetry: Precision Maps for Ground Control and Directly Georeferenced Surveys: 3-D Uncertainty-Based Change Detection for SfM Surveys. Earth Surf. Process. Landf. 2017, 42, 1769–1788. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D Laser Scanner in the Assessment of Erosion and Deposition Volumes and Channel Change in a Proglacial River. Earth Surf. Process. Landf. 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Harley, M.D. Coastal Storm Definition. In Coastal Storms: Processes and Impacts; Ciavola, P., Coco, G., Eds.; John Wiley & Sons: Chichester, UK; Hoboken, NJ, USA, 2017; ISBN 978-1-118-93710-5. [Google Scholar]
- Boccotti, P. Idraulica Marittima; UTET: Torino, Italy, 1997; ISBN 978-88-02-05308-0. [Google Scholar]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical Parameterization of Setup, Swash, and Runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Armaroli, C.; Ciavola, P.; Masina, M.; Perini, L. Run-up Computation behind Emerged Breakwaters for Marine Strom Risk Assessment. J. Coast. Res. 2009, 2, 1612–1616. [Google Scholar]
- Van der Meer, J.W.; Daemen, I.F.R. Stability and Wave Transmission at Low-Crested Rubble-Mound Structures. J. Waterw. Port Coast. Ocean Eng. 1994, 120, 1–19. [Google Scholar] [CrossRef]
- Perini, L.; Calabrese, L. Il Sistema Mare-Costa dell’Emilia-Romagna; Pendragon: Bologna, Italy, 2010; ISBN 978-88-8342-848-7. [Google Scholar]
- Pirazzoli, P.A.; Tomasin, A. Recent Abatement of Easterly Winds in the Northern Adriatic. Int. J. Climatol. 1999, 19, 1205–1219. [Google Scholar] [CrossRef]
- Fryberger, S.G. Techniques for the Evaluation of Surface Wind Data in Terms of Eolian Sand Drift–Open-File Report 78-405; U.S. Geological Survey: Reston, VA, USA, 1978.
- Kalma, J.D.; Speight, J.G.; Wasson, R.J. Potential Wind Erosion in Australia: A Continental Perspective. J. Climatol. 1988, 8, 411–428. [Google Scholar] [CrossRef]
- McKee, E.D. Sedimentary structures in dunes. In A Study of Global Sand Seas; McKee, E.D., Ed.; U.S. Geological Survey: Reston, VA, USA, 1979; pp. 83–136. [Google Scholar]
- Bagnold, R.A. The Transport of Sand by Wind. Geogr. J. 1937, 89, 409. [Google Scholar] [CrossRef]
- Lettau, K.; Lettau, H.H. Experimental and micro-meteorological field studies of dune migration. In Exploring the World’s Driest Climate; Lettau, H.H., Lettau, K., Eds.; University of Wisconsin-Madison: Madison, WI, USA, 1978; pp. 110–147. [Google Scholar]
- Bagnold, R.A. The Physics of Blown Sand and Desert Dunes; Methuen: London, UK, 1941. [Google Scholar]
- Belly, P.Y. Sand Movement by Wind; Hydraulic Engineering Reports; USACE: Washington, WA, USA, 1964; p. 84.
- Pearce, K.I.; Walker, I.J. Frequency and Magnitude Biases in the ‘Fryberger’ Model, with Implications for Characterizing Geomorphically Effective Winds. Geomorphology 2005, 68, 39–55. [Google Scholar] [CrossRef]
- Wilson, I.G. Desert Sand Flow Basins and a Model for the Development of Ergs. Geogr. J. 1971, 137, 180–199. [Google Scholar] [CrossRef]
- Tsoar, H. Dynamic Processes Acting on a Longitudinal (Seif) Sand Dune. Sedimentology 1983, 30, 567–578. [Google Scholar] [CrossRef]
- Lancaster, N.; Baas, A. Influence of Vegetation Cover on Sand Transport by Wind: Field Studies at Owens Lake, California. Earth Surf. Process. Landf. 1998, 23, 69–82. [Google Scholar] [CrossRef]
- Arens, S.M. Transport Rates and Volume Changes in a Coastal Foredune on a Dutch Wadden Island. J. Coast. Conserv. 1997, 3, 49–56. [Google Scholar] [CrossRef]
- Bullard, J.E. A Note on the Use of the “Fryberger Method” for Evaluating Potential Sand Transport by Wind. J. Sediment. Res. 1997, 67, 499–501. [Google Scholar] [CrossRef]
- Miot da Silva, G.; Hesp, P. Coastline Orientation, Aeolian Sediment Transport and Foredune and Dunefield Dynamics of Moçambique Beach, Southern Brazil. Geomorphology 2010, 120, 258–278. [Google Scholar] [CrossRef]
- Zingg, A. Wind Tunnel Studies of the Movement of Sedimentary Material. In Proceedings of the 5th Hydraulics Conference Bulletin, Iowa City, IA, USA, 9–11 June 1953; Institute of Hydraulics: Iowa City, IA, USA, 1953; Volume 34, pp. 111–135. [Google Scholar]
- Armaroli, C.; Grottoli, E.; Harley, M.D.; Ciavola, P. Beach Morphodynamics and Types of Foredune Erosion Generated by Storms along the Emilia-Romagna Coastline, Italy. Geomorphology 2013, 199, 22–35. [Google Scholar] [CrossRef]
- Cook, K.L. An Evaluation of the Effectiveness of Low-Cost UAVs and Structure from Motion for Geomorphic Change Detection. Geomorphology 2017, 278, 195–208. [Google Scholar] [CrossRef]
- Phillips, M.S.; Blenkinsopp, C.E.; Splinter, K.D.; Harley, M.D.; Turner, I.L.; Cox, R.J. High-Frequency Observations of Berm Recovery Using a Continuous Scanning Lidar. In Proceedings of the Australasian Coasts and Ports 2017 Conference, Cairns, Australia, 23 June 2017; pp. 872–878. [Google Scholar]
- Rajabi, M.R.; Rohani, F.; Ekhtessassi, M.R.; Ghazanfarpoor, N. Morphodynamic Anlysis of Wind Faces Using Spatial Sand Rose Model in Zabol and Zahak Region, Iran. Biaban J. 2006, 11, 45–51. [Google Scholar]
- Ahmadi, H.; Mesbahzadeh, T. Comparison of Sand Drifts Potential Stimating, Using Momentum Method and Fryberger Velocity Classes Method (Case Study: Jask and Kerman). J. Water Soil Agric. Sci. Technol. 2011, 25, 11–18. [Google Scholar]
- Namikas, S.L.; Sherman, D.J. A Review of the Effects of Surface Moisture Content on Aeolian Sand Transport. In Desert Aeolian Processes; Tchakerian, V.P., Ed.; Springer: Dordrecht, The Netherlands, 1995; pp. 269–293. ISBN 978-94-010-6519-1. [Google Scholar]
- Davidson-Arnott, R.G.D.; Yang, Y.; Ollerhead, J.; Hesp, P.A.; Walker, I.J. The Effects of Surface Moisture on Aeolian Sediment Transport Threshold and Mass Flux on a Beach. Earth Surf. Process. Landf. 2008, 33, 55–74. [Google Scholar] [CrossRef]
- Lynch, K.; Jackson, D.W.T.; Cooper, J.A.G. The Fetch Effect on Aeolian Sediment Transport on a Sandy Beach: A Case Study from Magilligan Strand, Northern Ireland. Earth Surf. Process. Landf. 2016, 41, 1129–1135. [Google Scholar] [CrossRef] [Green Version]









| ID | Start | End | RDD 1 | RDP [VU] | RDD/DP |
|---|---|---|---|---|---|
| AE 1 | 28 December 2016 23:40 | 29 December 2016 11:10 | −24 °N (NNW) | 365.6 | 0.985 |
| AE 2 | 5 January 2017 9:20 | 6 January 2017 23:40 | 243 °N (WSW) | 325.2 | 0.958 |
| AE 3 | 16 January 2017 2:00 | 19 January 2017 7:50 | 247 °N (WSW) | 917.7 | 0.995 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duo, E.; Fabbri, S.; Grottoli, E.; Ciavola, P. Uncertainty of Drone-Derived DEMs and Significance of Detected Morphodynamics in Artificially Scraped Dunes. Remote Sens. 2021, 13, 1823. https://doi.org/10.3390/rs13091823
Duo E, Fabbri S, Grottoli E, Ciavola P. Uncertainty of Drone-Derived DEMs and Significance of Detected Morphodynamics in Artificially Scraped Dunes. Remote Sensing. 2021; 13(9):1823. https://doi.org/10.3390/rs13091823
Chicago/Turabian StyleDuo, Enrico, Stefano Fabbri, Edoardo Grottoli, and Paolo Ciavola. 2021. "Uncertainty of Drone-Derived DEMs and Significance of Detected Morphodynamics in Artificially Scraped Dunes" Remote Sensing 13, no. 9: 1823. https://doi.org/10.3390/rs13091823
APA StyleDuo, E., Fabbri, S., Grottoli, E., & Ciavola, P. (2021). Uncertainty of Drone-Derived DEMs and Significance of Detected Morphodynamics in Artificially Scraped Dunes. Remote Sensing, 13(9), 1823. https://doi.org/10.3390/rs13091823