A Zoning Earthquake Casualty Prediction Model Based on Machine Learning
Abstract
:1. Introduction
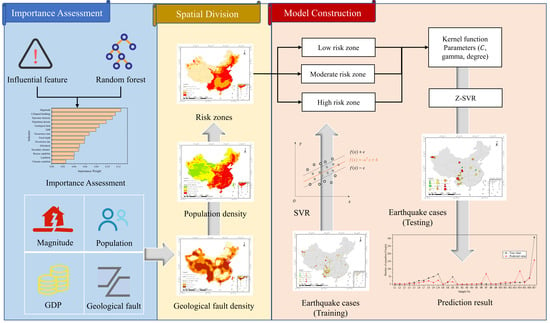
2. Materials and Methods
2.1. Study Area
2.2. Materials
2.2.1. Earthquake Case Dataset
2.2.2. Geological Fault Dataset
2.2.3. Population Dataset
2.3. Methods
3. Spatial Division
3.1. Importance Assessment
- Inputs: Disaster-inducing factors (7 variables), disaster-affected bodies (4 variables) and disaster-formative environments (3 variables).
- Parameters: Number of estimators = 150, criterion = ‘squared_error’, max depth = 6, min samples split = 2, min samples leaf = 1, min weight fraction leaf = 0.0, max features = ‘auto’, max leaf nodes = None, min impurity decrease = 0.0, bootstrap = Frue, oob score = False, number of jobs = None, random state = None, verbose = 0, warm start = False, ccp_alpha = 0.0, max samples = None.
- Step 1: Use bootstrap sampling to extract subtraining sets from the training set.
- Step 2: Generate the feature subsets by randomly selecting features before node splitting.
- Step 3: Establish decision trees.
- Step 4: Obtain the results for the sample to be tested.
- Step 5: Calculate the importance of the input parameters.
- Output: Importance weight of the prediction indicators.
3.2. Population Density
3.3. Geological Fault Density
3.4. Overlay Analysis
4. Prediction Model
4.1. Algorithm
4.2. Model Construction
5. Results
5.1. Spatial Division of the Study Area
5.2. Prediction Result of Z-SVR Model
6. Discussion
6.1. Comparison between Z-SVR and Other Models
6.1.1. Cross-Validation
6.1.2. Regression Accuracy Evaluation
6.1.3. Classification Accuracy Evaluation
6.2. Future Work
7. Conclusions
- Among all selected features from the evaluation index system, the order of importance from high to low is as follows: magnitude, collapsed buildings, epicenter intensity, population density, geological fault density, GDP, occurrence time, focal depth, occurrence day, aftershock, secondary disaster, rescue capability, landform, and climatic condition.
- The proposed method of spatial division based on regional diversity could be used as an effective tool to refine complex study areas. Using this method, we divided China’s mainland into high, moderate, and low risk zones, which laid the foundation for the construction of a prediction model with submodels that are suitable for different risk zones. The verification results demonstrated that the proposed division method is feasible for classifying study regions, especially those with vast area and complex environments.
- The proposed Z-SVR model realizes accurate prediction and good generalization performance. We collected 143 historical earthquake cases, of which 113 cases were selected as the training dataset and 30 for examining the prediction performance of the model. The best model parameters were selected for each risk zone, which led to precise prediction results in risk zones of various grades. The proposed model also showed accurate regression and classification accuracy in the various risk zones compared with other machine learning models, including RF, BP and LR. Moreover, the proposed Z-SVR model was compared to the initial SVR model using the same database. Similar experiments were also implemented on comparative machine learning models, and we found that the prediction performances of all models with spatial division significantly improved. The above results prove the advantages and significance of the proposed model and spatial division method.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Weng, W.G.; Huang, Z.L. A scenario-based model for earthquake emergency management effectiveness evaluation. Technol. Forecast. Soc. 2018, 128, 197–207. [Google Scholar] [CrossRef]
- Alizadeh, M.; Zabihi, H.; Rezaie, F.; Asadzadeh, A.; Wolf, I.D.; Langat, P.K.; Khosravi, I.; Beiranvand Pour, A.; Mohammad Nataj, M.; Pradhan, B. Earthquake Vulnerability Assessment for Urban Areas Using an ANN and Hybrid SWOT-QSPM Model. Remote Sens. 2021, 13, 4519. [Google Scholar] [CrossRef]
- Schilling, J.; Hertig, E.; Tramblay, Y.; Scheffran, J. Climate change vulnerability, water resources and social implications in North Africa. Reg. Environ. Chang. 2020, 20, 15. [Google Scholar] [CrossRef] [Green Version]
- Yariyan, P.; Zabihi, H.; Wolf, I.D.; Karami, M.; Amiriyan, S. Earthquake risk assessment using an integrated Fuzzy Analytic Hierarchy Process with Artificial Neural Networks based on GIS: A case study of Sanandaj in Iran. Int. J. Disaster Risk Re. 2020, 50, 101705. [Google Scholar] [CrossRef]
- Jian, W. The Research of Earthquake Information Extraction and Assessment Based on Object-Oriented Technology with Remotely-Sensed Data. Doctor’s Thesis, Wuhan University, Wuhan, China, 5 June 2010. [Google Scholar]
- Zhu, Y.; Diao, F.; Fu, Y.; Liu, C.; Xiong, X. Slip rate of the seismogenic fault of the 2021 Maduo earthquake in western China inferred from GPS observations. Sci. China Earth Sci. 2021, 64, 1363–1370. [Google Scholar] [CrossRef]
- Chen, L.; Huang, Y.; Bai, R.; Chen, A. Regional disaster risk evaluation of China based on the universal risk model. Nat. Hazards 2017, 89, 647–660. [Google Scholar] [CrossRef]
- Zhou, W.; Guo, S.; Deng, X.; Xu, D. Livelihood resilience and strategies of rural residents of earthquake-threatened areas in Sichuan Province, China. Nat. Hazards 2021, 106, 255–275. [Google Scholar] [CrossRef]
- National Earthquake Emergency Plan. Available online: http://www.gov.cn/yjgl/2012-09/21/content_2230337.htm (accessed on 17 May 2021).
- Maqsood, S.T.; Schwarz, J. Estimation of Human casualties from earthquakes in Pakistan—An engineering approach. Seismol. Res. Lett. 2011, 82, 32–41. [Google Scholar] [CrossRef]
- Guangxian, X. Rapid assessment of disaster losses in post-earthquake. J. Catastrophology 1991, 4, 12–17. [Google Scholar]
- Jaiswal, K.; Wald, D. An empirical model for global earthquake fatality estimation. Earthq. Spectra 2010, 26, 1017–1037. [Google Scholar] [CrossRef] [Green Version]
- ATC. Earthquake Damage Evaluation Data for California (ATC-13); Applied Technology Commission: Redwood City, CA, USA, 1985. [Google Scholar]
- Ceferino, L.; Kiremidjian, A.; Deierlein, G. Probabilistic model for regional multiseverity casualty estimation due to building damage following an earthquake. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civil. Eng. 2018, 4, 4018023. [Google Scholar] [CrossRef]
- Xianfu, B.; Gaozhong, N.; Yuqian, D.; Qingkun, Y.; Weidong, L.; Liaoyuan, Y. Modeling and Testing Earthquake-induced Landslide Casualty Rate Based on a Grid in a Kilometer Scale: Taking the 2014 Yunnan Ludian MS6. 5 Earthquake as a Case. J. Seismol. Res. 2021, 44, 87–95. [Google Scholar]
- Stav, S.; Lena, N.; Yaron, B.D.; Limor, A.D.; Asim, Z. An Integrated and Interdisciplinary Model for Predicting the Risk of Injury and Death in Future Earthquakes. PLoS ONE 2016, 11, e151111. [Google Scholar]
- Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2020, 101, 107038. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Y.; Shan, X.; Zhu, C. Earthquake Magnitude Estimation from High-Rate GNSS Data: A Case Study of the 2021 Mw 7.3 Maduo Earthquake. Remote Sens. 2021, 13, 4478. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Miyajima, M.; Hassanzadeh, R.; Amiraslanzadeh, R.; Kamel, B. A GIS-based seismic hazard, building vulnerability and human loss assessment for the earthquake scenario in Tabriz. Soil. Dyn. Earthq. Eng. 2014, 66, 263–280. [Google Scholar] [CrossRef]
- Feng, T.; Hong, Z.; Fu, Q.; Ma, S.; Jie, X.; Wu, H.; Jiang, C.; Tong, X. Application and prospect of a high-resolution remote sensing and geo-information system in estimating earthquake casualties. Nat. Hazards Earth Syst. Sci. 2014, 1, 7137–7166. [Google Scholar] [CrossRef] [Green Version]
- Wenjuan, Z. Design of the Population Casualty Acquisition and Evaluation System in Earthquake Disaster Areas Based on Mobile Communication Big Data. China Earthq. Eng. J. 2019, 41, 1066–1071. [Google Scholar]
- Huang, X.; Zhou, Z.; Wang, S. The prediction model of earthquake casuailty based on robust wavelet v-SVM. Nat. Hazards 2015, 77, 717–732. [Google Scholar]
- Gul, M.; Guneri, A.F. An artificial neural network-based earthquake casualty estimation model for Istanbul city. Nat. Hazards 2016, 84, 2163–2178. [Google Scholar] [CrossRef]
- Jia, H.; Lin, J.; Liu, J. An Earthquake Fatalities Assessment Method Based on Feature Importance with Deep Learning and Random Forest Models. Sustainability 2019, 11, 2727. [Google Scholar] [CrossRef] [Green Version]
- Sousa, J.J.; Liu, G.; Fan, J.; Perski, Z.; Steger, S.; Bai, S.; Wei, L.; Salvi, S.; Wang, Q.; Tu, J. Geohazards Monitoring and Assessment Using Multi-Source Earth Observation Techniques. Remote Sens. 2021, 13, 4269. [Google Scholar] [CrossRef]
- Shi, P. Natural Disasters in China; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Wen, L.; Wenkai, C.; Zhonghong, Z. Assessing the applicability of life vulnerability models for earthquake disasters in typical regions of China. J. Beijing Norm. Univ. 2019, 55, 284–290. [Google Scholar]
- Tingting, Z. Assessment of Earthquake Fatality and Disaster Degree Based on Spatio-Temporal Method. Bachelor’s Thesis, Beijing Normal University, Beijing, China, 3 June 2020. [Google Scholar]
- China Earthquake Administration. Compilation of Earthquake Disaster Loss Assessment in China’s Mainland; Seismological Press: Beijing, China, 1996. [Google Scholar]
- Monitoring and Forecasting Department of China Earthquake Administration. Compilation of Earthquake Disaster Loss Assessment in China’s Mainland; Seismological Press: Beijing, China, 2001. [Google Scholar]
- Earthquake Emergency Rescue Department of China Earthquake Administration. Compilation of Earthquake Disaster Loss Assessment in China’s Mainland from 2001 to 2005; Seismological Press: Beijing, China, 2010. [Google Scholar]
- Earthquake Emergency Rescue Department of China Earthquake Administration. Compilation of Earthquake Disaster Loss Assessment in China’s Mainland from 2006 to 2010; Seismological Press: Beijing, China, 2015. [Google Scholar]
- Liang, S.; Chen, D.; Li, D.; Qi, Y.; Zhao, Z. Spatial and Temporal Distribution of Geologic Hazards in Shaanxi Province. Remote Sens. 2021, 13, 4259. [Google Scholar] [CrossRef]
- Hoffmann, S.; Beierkuhnlein, C. Climate change exposure and vulnerability of the global protected area estate from an international perspective. Divers. Distrib. 2020, 26, 1496–1509. [Google Scholar] [CrossRef]
- Xiong, K.; Adhikari, B.R.; Stamatopoulos, C.A.; Zhan, Y.; Wu, S.; Dong, Z.; Di, B. Comparison of different machine learning methods for debris flow susceptibility mapping: A case study in the Sichuan Province, China. Remote Sens. 2020, 12, 295. [Google Scholar] [CrossRef] [Green Version]
- Peijun, S. Theory on Disaster Science and Disaster Dynamics. J. Nat. Disasters 2002, 11, 1–9. [Google Scholar]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve Bayes tree classifiers for a landslide susceptibility assessment in Langao County, China. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef] [Green Version]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation importance: A corrected feature importance measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Sun, Z.; Han, J. Landslide susceptibility modeling using integrated ensemble weights of evidence with logistic regression and random forest models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef] [Green Version]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Yuanyuan, L.; Guofeng, S.; Wenguo, W. A Review of Researches on Seismic Casualty Estimation. J. Catastrophology 2014, 29, 223–227. [Google Scholar]
- Fan, Y.; Baozhu, Z.; Liangliang, Y. System of Earthquake Casualty Assessment Based on BP Neural Network. Technol. Earthq. Disaster Prev. 2009, 4, 428–435. [Google Scholar]
- Zhao, K.; Jin, B.; Fan, H.; Song, W.; Zhou, S.; Jiang, Y. High-Performance Overlay Analysis of Massive Geographic Polygons That Considers Shape Complexity in a Cloud Environment. Int. J. Geo-Inf. 2019, 8, 290. [Google Scholar] [CrossRef] [Green Version]
- Thomas, S.; Pillai, G.N.; Pal, K. Prediction of peak ground acceleration using ϵ-SVR, v-SVR and Ls-SVR algorithm. Geomat. Nat. Hazards Risk 2017, 8, 177–193. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.Y.; Cheng, C.T.; Chau, K.W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Guirong, W.; Juan, Y.; Lixia, X. Machine Learning and Its Application; China Machine Press: Beijing, China, 2019. [Google Scholar]
- Tao, D.; Ma, Q.; Li, S.; Xie, Z.; Lin, D.; Li, S. Support Vector Regression for the Relationships between Ground Motion Parameters and Macroseismic Intensity in the Sichuan—Yunnan Region. Appl. Sci. 2020, 10, 3086. [Google Scholar] [CrossRef]
- Zhihua, Z. Machine Learning; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Chih-Chung, C.; Chih-Jen, L. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–39. [Google Scholar] [CrossRef]
- Ghorbani, M.; Zargar, G.; Jazayeri-Rad, H. Prediction of asphaltene precipitation using support vector regression tuned with genetic algorithms. Petroleum 2016, 2, 301–306. [Google Scholar] [CrossRef] [Green Version]
- Bamakan, S.; Wang, H.; Ravasan, A.Z. Parameters Optimization for Nonparallel Support Vector Machine by Particle Swarm Optimization. Procedia Comput. Sci. 2016, 91, 482–491. [Google Scholar] [CrossRef] [Green Version]
















| No. | Attribute | Description & Qualification |
|---|---|---|
| 1 | Occurrence day | There are 7 categories where 1~7 correspond to Monday to Sunday, respectively. |
| 2 | Occurrence time | The time when the earthquake occurred, which is defined as the minutes after 0:00 on the day. |
| 3 | Location | The province and city where the earthquake occurred, including longitude and latitude. |
| 4 | Magnitude | Defined as the surface wave magnitude. |
| 5 | Focal depth | The vertical distance from the hypocenter to the surface of the earth (km). |
| 6 | Epicenter intensity | Measured according to The China Seismic Intensity Scale (China’s national standard). |
| 7 | Aftershock | The number of shocks of magnitude greater than 5.0 after the occurrence of the main shock. |
| 8 | Geological fault density | The average density of strata faults in the earthquake-stricken area. |
| 9 | Landform | There are five categories, which are labelled 1 to 5, and represent plain, basin, hill, mountain and plateau, respectively. |
| 10 | Climatic condition | There are two levels where 0 indicates normal and 1 indicates abnormal. |
| 11 | Secondary disaster | There are two categories, where 0 indicates no secondary disaster and 1 indicates the occurrence of a secondary disaster. |
| 12 | Population density | The number of people who live in the earthquake-stricken area per square kilometer. |
| 13 | Collapsed buildings | The number of collapsed houses. |
| 14 | Rescue capability | There are three levels where 1 indicates lacking assignment, 2 indicates general assignment and 3 indicates improved assignment. |
| 15 | GDP | The ratio of GDP to the total population of the earthquake-stricken region. |
| 16 | Death toll | The number of casualties due to the earthquake. |
| Zone | Training Sample (Cases) | Testing Sample (Cases) | Total (Cases) |
|---|---|---|---|
| Low risk | 39 | 10 | 49 |
| Moderate risk | 10 | 3 | 13 |
| High risk | 64 | 17 | 81 |
| Total | 113 | 30 | 143 |
| Target Level | Rule Level | Index Level |
|---|---|---|
| Seismic fatality | Disaster-inducing factors | Magnitude |
| Epicenter intensity | ||
| Focal depth | ||
| Geological fault density | ||
| Occurrence time | ||
| Occurrence day | ||
| Aftershock | ||
| Disaster-affected bodies | Collapsed buildings | |
| Rescue capability | ||
| Population density | ||
| GDP | ||
| Disaster-formative environments | Climatic condition | |
| Landform | ||
| Secondary disaster |
| Type | Expression 1 |
|---|---|
| Linear kernel | |
| Gaussian kernel | |
| Polynomial kernel | |
| Sigmoid kernel |
| Zone | Kernel Function | Parameters |
|---|---|---|
| Lowisk | Gaussian kernel | = 100, gamma = 0.1 |
| Moderate risk | Gaussian kernel | = 100, gamma = 1 |
| High risk | Gaussian kernel | = 1000, gamma = 0.1 |
| Sample No. | Time | Place | True Value | Predicted Value |
|---|---|---|---|---|
| L1 | 1989/9/22 | Xiaojin | 1 | 4.6 |
| L3 | 1986/8/7 | Litang | 2 | 1.2 |
| L7 | 2017/8/8 | Jiuzhaigou | 25 | 15.8 |
| M1 | 1991/3/26 | Datong-Yanggao | 1 | 1.1 |
| M2 | 2005/11/26 | Jiujiang-Ruichang | 13 | 17.8 |
| H8 | 1953/5/4 | Mile | 3 | 3 |
| H13 | 1965/1/13 | Yuanqu | 11 | 17.9 |
| H16 | 2008/8/30 | Renhe-Huili | 41 | 39.6 |
| Indicator | Model | Low Risk Zones | Moderate Risk Zones | High Risk Zones | Total |
|---|---|---|---|---|---|
| Z-SVR | 0.92 | 1 | 0.87 | 0.87 | |
| SVR | 0.92 | 0.5 | 0.47 | 0.63 | |
| Z-RF | 0.85 | 1 | 0.52 | 0.64 | |
| RF | 0.77 | 1 | 0.5 | 0.51 | |
| Z-BP | 0.72 | 0.83 | 1 | 0.94 | |
| BP | 0.87 | 0.83 | 0.71 | 0.67 | |
| Z-LR | 0.87 | 0.83 | 1 | 0.93 | |
| LR | 1 | 1 | 0.86 | 0.91 | |
| Z-SVR | 0.9 | 1 | 0.82 | 0.87 | |
| SVR | 0.9 | 0.67 | 0.47 | 0.63 | |
| Z-RF | 0.7 | 0.33 | 0.53 | 0.57 | |
| RF | 0.6 | 0.33 | 0.47 | 0.5 | |
| Z-BP | 0.5 | 0.67 | 0.76 | 0.67 | |
| BP | 0.6 | 0.67 | 0.65 | 0.63 | |
| Z-LR | 0.6 | 0.67 | 0.71 | 0.67 | |
| LR | 0.4 | 0.33 | 0.65 | 0.53 | |
| Z-SVR | 0.9 | 1 | 0.81 | 0.87 | |
| SVR | 0.9 | 0.56 | 0.46 | 0.63 | |
| Z-RF | 0.71 | 0.5 | 0.52 | 0.59 | |
| RF | 0.61 | 0.5 | 0.45 | 0.5 | |
| Z-BP | 0.54 | 0.67 | 0.87 | 0.74 | |
| BP | 0.63 | 0.67 | 0.64 | 0.65 | |
| Z-LR | 0.63 | 0.67 | 0.83 | 0.74 | |
| LR | 0.57 | 0.5 | 0.74 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Gong, A.; Zeng, T.; Bao, W.; Xu, C.; Huang, Z. A Zoning Earthquake Casualty Prediction Model Based on Machine Learning. Remote Sens. 2022, 14, 30. https://doi.org/10.3390/rs14010030
Li B, Gong A, Zeng T, Bao W, Xu C, Huang Z. A Zoning Earthquake Casualty Prediction Model Based on Machine Learning. Remote Sensing. 2022; 14(1):30. https://doi.org/10.3390/rs14010030
Chicago/Turabian StyleLi, Boyi, Adu Gong, Tingting Zeng, Wenxuan Bao, Can Xu, and Zhiqing Huang. 2022. "A Zoning Earthquake Casualty Prediction Model Based on Machine Learning" Remote Sensing 14, no. 1: 30. https://doi.org/10.3390/rs14010030
APA StyleLi, B., Gong, A., Zeng, T., Bao, W., Xu, C., & Huang, Z. (2022). A Zoning Earthquake Casualty Prediction Model Based on Machine Learning. Remote Sensing, 14(1), 30. https://doi.org/10.3390/rs14010030