A Joint Denoising Learning Model for Weight Update Space–Time Diversity Method †
Abstract
:1. Introduction
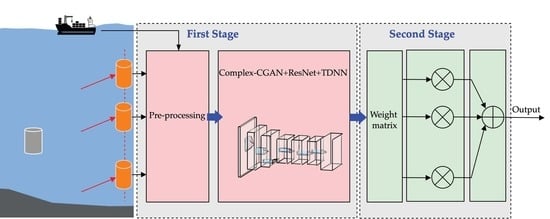
- To effectively suppress the nonlinear components contained in the VURN, we propose a CGAN-based residual cancellation learning model by referring to the structure of the KBM-ANC. The proposed model puts the received signal and the reference noise into the CGAN. A nonlinear mapping is created between them by performing “generative-adversarial”-based learning in CGAN to estimate noise . Then, the residual cancellation learning is performed by the RCL module to obtain the final noise-reduction estimate .
- To efficiently handle the complex-type characteristics of UWA signals, we propose a pre-processing structure for complex-type orthogonal compression. The proposed structure performs a complex convolution operation on the UWA signal to obtain separated real and imaginary features. The separated features are trained separately for noise-reduction to avoid the loss of complex-type data features. The separation of real and imaginary parts can lead to orthogonality corruption. To minimize the corruption, we normalize the orthogonal scale by compressing the real and imaginary features orthogonally. The proposed pre-processing method effectively fits the structure of the DM in the complex-CGAN, together with CReLU, and effectively improves the performance of the noise-reduction learning model for complex-type data.
- To effectively reduce the MAI due to CDMA signals, we propose an improved STD model. The model matches a weight matrix for each array element at the receiver. The model allows the main path signal to be enhanced and effectively reduces the influence of other multipath signals. Thus, the model reduces the correlation between signals and suppresses MAI in the system.
2. Related Works
3. System Model for UWA Communication
4. A Joint Denoising Learning Model for Weight Update STD Method
4.1. The UWA Signal Analysis and Pre-Processing
4.2. Noise-Reduction Learning Models Based on Complex-CGAN
4.3. The STD Model Based on Weight Update Strategy
5. Evaluation and Result Analysis
5.1. Simulation Results
5.2. Lake Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Climent, S.; Sanchez, A.; Capella, J.; Meratnia, N.; Serrano Martín, J. Underwater Acoustic Wireless Sensor Networks: Advances and Future Trends in Physical, MAC and Routing Layers. Sensors 2014, 14, 795–833. [Google Scholar] [CrossRef] [PubMed]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Andrew, C.; Jill, K.; Suleyman, S. Signal processing for underwater acoustic communications. IEEE Commun. Mag. 2009, 47, 90–96. [Google Scholar]
- Wan, L.; Zhou, H.; Xu, X.; Huang, Y.; Zhou, S.; Shi, Z.; Cui, J. Adaptive Modulation and Coding for Underwater Acoustic OFDM. IEEE J. Ocean. Eng. 2015, 40, 327–336. [Google Scholar] [CrossRef]
- Song, A.; Mohsen, B.; Song, H.C.; Hodgkiss, W.S.; Porter, M.B. Impact of ocean variability on coherent underwater acoustic communications during the Kauai experiment (KauaiEx). J. Acoust. Soc. Am. 2008, 123, 856–865. [Google Scholar] [CrossRef] [Green Version]
- Wong, K.T.; Zoltowski, M.D. Self-initiating MUSIC-based direction finding in underwater acoustic particle velocity-field beamspace. IEEE J. Ocean. Eng. 2000, 25, 262–273. [Google Scholar] [CrossRef]
- Yang, T.C. Deconvolved Conventional Beamforming for a Horizontal Line Array. IEEE J. Ocean. Eng. 2018, 43, 160–172. [Google Scholar] [CrossRef]
- Palmese, M.; Trucco, A. An Efficient Digital CZT Beamforming Design for Near-Field 3-D Sonar Imaging. IEEE J. Ocean. Eng. 2010, 35, 584–594. [Google Scholar] [CrossRef]
- Edwards, J.R.; Schmidt, H.; LePage, K.D. Bistatic synthetic aperture target detection and imaging with an AUV. IEEE J. Ocean. Eng. 2001, 26, 690–699. [Google Scholar] [CrossRef]
- Yahong, R.Z.; Jing, X.W.; Cheng, S.X. Turbo equalization for single-carrier underwater acoustic communications. IEEE Commun. Mag. 2015, 53, 79–87. [Google Scholar]
- Preisig, J.C.; Deane, G.B. Surface wave focusing and acoustic communications in the surf zone. J. Acoust. Soc. Am. 2004, 116, 2067–2080. [Google Scholar] [CrossRef]
- Guo, S.Z.; He, F.D. Spatial diversity in multichannel processing for underwater acoustic communications. Ocean Eng. 2011, 38, 1611–1623. [Google Scholar]
- Dahl, H.; Dall, O.; David, R. Range-Dependent Inversion for Seabed Parameters Using Vector Acoustic Measurements of Underwater Ship Noise. IEEE J. Ocean. Eng. 2021, 1, 1–10. [Google Scholar] [CrossRef]
- He, C.; Huo, S.Y.; Zhang, Q.F.; Wang, H.; Huang, J.G. Multi-channel iterative FDE for single carrier block transmission over underwater acoustic channels. China Commun. 2015, 12, 55–61. [Google Scholar] [CrossRef]
- Cao, Y.; Shi, W.; Sun, L.J.; Fu, X.M. Frequency Diversity Based Underwater Acoustic Passive Localization. IEEE Internet Things J. 2021, 1, 1. [Google Scholar] [CrossRef]
- Ian, F.A.; Dario, P.; Tommaso, M. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar]
- Peng, L.S. Image denoising algorithm via doubly local Wiener filtering with directional windows in wavelet domain. IEEE Signal Process. Lett. 2005, 12, 681–684. [Google Scholar] [CrossRef]
- Astola, J.; Haavisto, P.; Neuvo, Y. Vector median filters. Proc. IEEE Inst. Electr. Electron. Eng. 1990, 78, 678–689. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef] [Green Version]
- Rout, D.K.; Subudhi, B.N.; Veerakumar, T.; Chaudhury, S. Walsh–Hadamard-Kernel-Based Features in Particle Filter Framework for Underwater Object Tracking. IEEE Trans. Industr. Inform. 2020, 16, 5712–5722. [Google Scholar] [CrossRef]
- Comaniciu, D.; Ramesh, V.; Meer, P. Kernel-based object tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 564–577. [Google Scholar] [CrossRef] [Green Version]
- Ferwerda, J.; Hainmueller, J.; Hazlett, C.J. Kernel-based regularized least squares in R (KRLS) and Stata (krls). J. Stat. Softw. 2017, 79, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Kailath, T. RKHS approach to detection and estimation problems–I: Deterministic signals in Gaussian noise. IEEE Trans. Inf. Theory 1971, 17, 530–549. [Google Scholar] [CrossRef]
- Liu, W.; Príncipe, J.C. Kernel affine projection algorithms. Eurasip J. Adv. Signal Process. 2008, 2008, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Jackson, D.R.; Dowling, D.R. Phase conjugation in underwater acoustics. J. Acoust. Soc. Am. 1991, 89, 171–181. [Google Scholar] [CrossRef]
- Muller, K.R.; Mika, S.; Ratsch, G.; Tsuda, K.; Scholkopf, B. An introduction to kernel-based learning algorithms. IEEE Trans. Neural Netw. Learn Syst. 2001, 12, 181–201. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Zou, Y.X.; Wang, W.W. Learning soft mask with DNN and DNN-SVM for multi-speaker DOA estimation using an acoustic vector sensor. J. Franklin Inst. 2018, 355, 1692–1709. [Google Scholar] [CrossRef]
- Ridao, P.; Tiano, A.; El-Fakdi, A.; Carreras, M.; Zirilli, A. On the identification of nonlinear models of unmanned underwater vehicles. Control Eng. Pract. 2004, 12, 1483–1499. [Google Scholar] [CrossRef]
- Li, Y.; Lu, H.; Li, J.; Li, X.; Li, Y.; Serikawa, S. Underwater image de-scattering and classification by deep neural network. Comput. Electr. Eng. 2016, 54, 68–77. [Google Scholar] [CrossRef]
- Tazebay, M.V.; Akansu, A.N. Adaptive subband transforms in time–frequency excisers for DSSS communications systems. IEEE Trans. Signal Process. 1995, 43, 2776–2782. [Google Scholar] [CrossRef]
- Hara, S.; Prasad, R. Overview of multicarrier CDMA. IEEE Commun. Mag. 1997, 35, 126–133. [Google Scholar] [CrossRef]
- Zhang, J.; Chong, E.K.; Tse, D.N.C. Output MAI distributions of linear MMSE multiuser receivers in DS-CDMA systems. IEEE Trans. Inf. Theory 2001, 47, 1128–1144. [Google Scholar] [CrossRef]
- Nagatsuka, M.; Kohno, R. A spatially and temporally optimal multi-user receiver using an array antenna for DS/CDMA. IEICE Trans. Commun. 1995, 78, 1489–1497. [Google Scholar]
- Sun, J.; Li, X.; Chen, K.; Cui, W.; Chu, M. A novel CMA+DDLMS blind equalization algorithm for underwater acoustic communication. Comput. J. 2020, 63, 974–981. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, F.L. Blind equalization based on RLS algorithm using adaptive forgetting factor for underwater acoustic channel. China Ocean Eng. 2014, 28, 401–408. [Google Scholar] [CrossRef]
- Shi, Y.; Konar, A.; Sidiropoulos, N.D.; Mao, X.P.; Liu, Y.T. Learning to beamform for minimum outage. IEEE Trans. Signal Process. 2018, 66, 5180–5193. [Google Scholar] [CrossRef]
- Chen, J.C.; Yao, K.; Hudson, R.E. Source localization and beamforming. IEEE Signal Process. Mag. 2002, 66, 30–39. [Google Scholar] [CrossRef] [Green Version]
- Vukadin, P.; Hudec, G. Acoustic telemetry system for underwater control. IEEE J. Ocean. Eng. 1991, 16, 142–145. [Google Scholar] [CrossRef]
- Wen, Q.; Ritcey, J.A. Spatial diversity equalization applied to underwater communications. IEEE J. Ocean. Eng. 1994, 19, 227–241. [Google Scholar]
- Li, S.; Smith, P.J.; Dmochowski, P.A.; Yin, J. Analysis of analog and digital MRC for distributed and centralized MU-MIMO systems. IEEE Trans. Veh. Technol. 2018, 68, 1948–1952. [Google Scholar] [CrossRef]
- Qu, F.; Wang, Z.; Yang, L. Differential orthogonal space–time block coding modulation for time-variant underwater acoustic channels. IEEE J. Ocean. Eng. 2016, 42, 188–198. [Google Scholar] [CrossRef]
- Mitran, P.; Ochiai, H.; Tarokh, V. Space-time diversity enhancements using collaborative communications. IEEE Trans. Inf. Theory 2005, 51, 2041–2057. [Google Scholar] [CrossRef]
- Stojanovic, M.; Freitag, L. Multichannel detection for wideband underwater acoustic CDMA communications. IEEE J. Ocean. Eng. 2006, 31, 685–695. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.F.; Zoltowski, M.D.; Ramos, J.; Chatterjee, C.; Roychowdhury, V.P. Reduced-dimension blind space–time 2-D RAKE receivers for DS-CDMA communication systems. IEEE Trans. Signal Process. 2000, 48, 1521–1536. [Google Scholar] [CrossRef]
- Elad, M.; Feuer, A. Superresolution restoration of an image sequence: Adaptive filtering approach. IEEE Trans. Image Process. 1999, 8, 387–395. [Google Scholar] [CrossRef] [Green Version]
- Eleftheriou, E.; Falconer, D. Tracking properties and steady-state performance of RLS adaptive filter algorithms. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1097–1110. [Google Scholar] [CrossRef]
- Malinowski, S.J.; Gloza, I. Underwater noise characteristics of small ships. Acta Acust. United Acust. 2002, 88, 718–721. [Google Scholar]
- Goel, A.; Vetteth, A.; Rao, K.R.; Sridhar, V. Active cancellation of acoustic noise using a self-tuned filter. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 2148–2156. [Google Scholar] [CrossRef]
- Sriperumbudur, B.K.; Fukumizu, K.; Lanckriet, G.R. Universality, Characteristic Kernels and RKHS Embedding of Measures. J. Mach. Learn Res. 2011, 12, 2389–2410. [Google Scholar]
- Wu, Q.; Li, Y.; Zakharov, Y.V.; Xue, W.; Shi, W. A kernel affine projection-like algorithm in reproducing kernel hilbert space. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 2249–2253. [Google Scholar] [CrossRef]
- Mitra, V.; Wang, C.J.; Banerjee, S. Lidar detection of underwater objects using a neuro-SVM-based architecture. IEEE Trans. Neural Netw. 2006, 17, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Boloix, R.; Murillo, J.J.; Tsaftaris, S.A. The generalized complex kernel least-mean-square algorithm. IEEE Trans. Signal Process. 2019, 67, 5213–5222. [Google Scholar] [CrossRef]
- Dhanalakshmi, P.; Palanivel, S.; Ramalingam, V. Classification of audio signals using SVM and RBFNN. Expert Syst. Appl. 2009, 36, 6069–6075. [Google Scholar] [CrossRef]
- Verma, N.K.; Singh, S. Image sequence prediction using ANN and RBFNN. Int. J. Image Graph 2013, 13, 1340006. [Google Scholar] [CrossRef]
- Stoffel, M.; Gulakala, R.; Bamer, F.; Markert, B. Artificial neural networks in structural dynamics: A new modular radial basis function approach vs. convolutional and feedforward topologies. Comput. Methods Appl. Mech. Eng. 2020, 364, 112989. [Google Scholar] [CrossRef]
- Petroni, S.; Tripoli, G.; Combi, C.; Vigna, B.; De Vittorio, M.; Todaro, M.T.; Passaseo, A. Noise reduction in GaN-based radio frequencysurface acoustic wave filters. Appl. Phys. Lett. 2004, 85, 1039–1041. [Google Scholar] [CrossRef]
- Xiao, C.; Wang, X.; Dou, H.; Li, H.; Lv, R.; Wu, Y.; Song, G.; Wang, W.; Zhai, R. Non-Uniform Synthetic Aperture Radiometer Image Reconstruction Based on Deep Convolutional Neural Network. Remote Sens. 2022, 14, 2359. [Google Scholar] [CrossRef]
- Chandrakala, S.; Rajeswari, N. Representation Learning Based Speech Assistive System for Persons With Dysarthria. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1510–1517. [Google Scholar] [CrossRef]
- Zhou, W.; Zhu, Z. A novel BNMF-DNN based speech reconstruction method for speech quality evaluation under complex environments. Int. J. Mach. Learn. Cybern. 2021, 12, 959–972. [Google Scholar] [CrossRef]
- He, C.B.; Huang, J.G.; Ding, Z. A Variable-Rate Spread-Spectrum System for Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2009, 34, 624–633. [Google Scholar]
- Rahmati, M.; Pompili, D. UNISeC: Inspection, Separation, and Classification of Underwater Acoustic Noise Point Sources. IEEE J. Ocean. Eng. 2018, 43, 777–791. [Google Scholar] [CrossRef]
- Wang, N.Y.; Wang, H.S.; Wang, T.W.; Fu, S.W.; Lu, X.; Wang, H.M.; Tsao, Y. Improving the Intelligibility of Speech for Simulated Electric and Acoustic Stimulation Using Fully Convolutional Neural Networks. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 29, 184–195. [Google Scholar] [CrossRef] [PubMed]
- George, E.B.; Smith, M.J. Speech analysis/synthesis and modification using an analysis-by-synthesis/overlap-add sinusoidal model. IEEE Trans. Speech Audio Process. 1997, 5, 389–406. [Google Scholar] [CrossRef]
- Li, Y.; Fu, R.; Meng, X.C.; Jin, W.; Shao, F. A SAR-to-Optical Image Translation Method Based on Conditional Generation Adversarial Network (cGAN). IEEE Access 2020, 8, 60338–60343. [Google Scholar] [CrossRef]
- Guo, X.; Nie, R.; Cao, J.; Zhou, D.; Mei, L.; He, K. FuseGAN: Learning to fuse multi-focus image via conditional generative adversarial network. IEEE Trans. Multimed. 2019, 21, 1982–1996. [Google Scholar] [CrossRef]
- Shao, Z.; Lu, Z.; Ran, M.; Fang, L.; Zhou, J.; Zhang, Y. Residual encoder–decoder conditional generative adversarial network for pansharpening. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1573–1577. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Chen, B.M. MLFcGAN: Multilevel feature fusion-based conditional GAN for underwater image color correction. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1488–1492. [Google Scholar] [CrossRef] [Green Version]
- Kim, M. ML/CGAN: Network Attack Analysis Using CGAN as Meta-Learning. IEEE Commun. Lett. 2021, 25, 499–502. [Google Scholar] [CrossRef]
- Deng, J.; Pang, G.Y.; Zhang, Z.Y.; Pang, Z.B.; Yang, H.Y.; Yang, G. cGAN Based Facial Expression Recognition for Human-Robot Interaction. IEEE Access 2019, 7, 9848–9859. [Google Scholar] [CrossRef]
- Rossi, R.; Murari, A.; Gaudio, P. On the Potential of Time Delay Neural Networks to Detect Indirect Coupling between Time Series. Remote Sens. 2020, 22, 584. [Google Scholar] [CrossRef]
- Miron, M.; Barclay, D.R.; Bousquet, J.F. The Oceanographic Sensitivity of the Acoustic Channel in Shallow Water. IEEE J. Ocean. Eng. 2021, 46, 675–686. [Google Scholar] [CrossRef]























| Parameters | Values of the Simulations and Lake Trial |
|---|---|
| Bandwidth | 5 kHz |
| Carrier frequency | 10 kHz |
| Spread spectrum code | 7-order m-sequence |
| Filter roll-off factor | 0.25 |
| Bit rate | 26.5 bps |
| Frame synchronization signal pulse width | LFM (50 ms) |
| Carrier synchronization | 2-order phase-locked loop |
| Channel coding | 1/2 convolutional codes |
| Network | Components, Kernel Size | Component Number |
|---|---|---|
| Conv, | GM 3; DM 6. | |
| Conv, | GM 3; DM 3. | |
| Conv, | GM 1. | |
| Complex-CGAN | Pool, | GM 1; DM 2. |
| CatBN | GM 1; DM 1. | |
| CReLU | GM 1; DM 1. | |
| Conv, | 2 | |
| Conv, | 3 | |
| RCL module | Inception | 1 |
| Pool, | 2 | |
| CReLU | 2 | |
| Conv, | 2 | |
| TDNN | CReLU | 1 |
| Angle | Method | RMSE | BER |
|---|---|---|---|
| Wiener + STD | 0.5520 | 0.81 × 10−2 | |
| KBM-ANC + STD | 0.4638 | 0.60 × 10−2 | |
| CNN + STD | 0.4527 | 0.52 × 10−2 | |
| Ours1 + STD | 0.4104 | 0.32 × 10−2 | |
| Wiener + Ours2 | 0.3698 | 0.77 × 10−3 | |
| KBM-ANC + Ours2 | 0.2239 | 0.55 × 10−3 | |
| CNN + Ours2 | 0.2013 | 0.19 × 10−3 | |
| Ours1 + Ours2 | 0.1804 | 0.45 × 10−4 | |
| Wiener + STD | 0.5201 | 0.79 × 10−2 | |
| KBM-ANC + STD | 0.4723 | 0.62 × 10−2 | |
| CNN + STD | 0.4387 | 0.49 × 10−2 | |
| Ours1 + STD | 0.3912 | 0.38 × 10−2 | |
| Wiener + Ours2 | 0.3741 | 0.74 × 10−3 | |
| KBM-ANC + Ours2 | 0.2187 | 0.52 × 10−3 | |
| CNN + Ours2 | 0.1922 | 0.21 × 10−3 | |
| Ours1 + Ours2 | 0.1732 | 0.49 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhang, D.; Han, Z.; Jiang, P. A Joint Denoising Learning Model for Weight Update Space–Time Diversity Method. Remote Sens. 2022, 14, 2430. https://doi.org/10.3390/rs14102430
Zhang Y, Zhang D, Han Z, Jiang P. A Joint Denoising Learning Model for Weight Update Space–Time Diversity Method. Remote Sensing. 2022; 14(10):2430. https://doi.org/10.3390/rs14102430
Chicago/Turabian StyleZhang, Yu, Dan Zhang, Zhen Han, and Peng Jiang. 2022. "A Joint Denoising Learning Model for Weight Update Space–Time Diversity Method" Remote Sensing 14, no. 10: 2430. https://doi.org/10.3390/rs14102430
APA StyleZhang, Y., Zhang, D., Han, Z., & Jiang, P. (2022). A Joint Denoising Learning Model for Weight Update Space–Time Diversity Method. Remote Sensing, 14(10), 2430. https://doi.org/10.3390/rs14102430