A Universal Multi-Frequency Micro-Resistivity Array Imaging Method for Subsurface Sensing
Abstract
:1. Introduction
2. Methodology
3. Result and Discussion
3.1. System Design
3.2. Lab Experiment
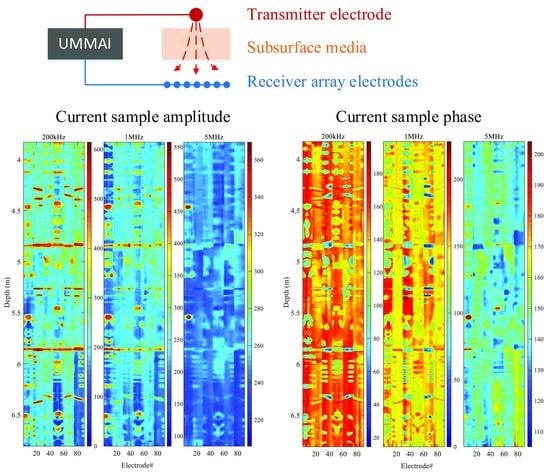
3.3. Field Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Zhuo, J.; Jiang, W.; Liu, Q.-H. 3-D Numerical Mode Matching Method for Off-Centered Electromagnetic Well Logging Tools in Noncircular Vertical Borehole and Invasion Zones in Multilayered Media. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Wu, T.; Yao, Z.; Qiu, A.; Li, Y.; Shi, Y. Fracture Identification in Well Logging Images: Two-Stage Adaptive Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Saavedra, L.; Rosa, G.-S.; Bergmann, J.-R. A Combined Mode-Matching Technique and Born Approximation Method to Model Well-Logging Sensors in Non-Axisymmetric Boreholes. IEEE Access 2021, 9, 84364–84374. [Google Scholar] [CrossRef]
- Tian, B.; Wang, L.; Kashiwaya, K.; Koike, K. Combination of Well-Logging Temperature and Thermal Remote Sensing for Characterization of Geothermal Resources in Hokkaido, Northern Japan. Remote Sens. 2015, 7, 2647. [Google Scholar] [CrossRef] [Green Version]
- Abdi, O.; Uusitalo, J.; Kivinen, V.-P. Logging Trail Segmentation via a Novel U-Net Convolutional Neural Network and High-Density Laser Scanning Data. Remote Sens. 2022, 14, 349. [Google Scholar] [CrossRef]
- Sun, D.; Li, X.; Cao, Z.; Yong, J.; Zhang, D.; Zhuang, J. Acoustic Robust Velocity Measurement Algorithm Based on Variational Bayes Adaptive Kalman Filter. IEEE J. Ocean. Eng. 2021, 46, 183–194. [Google Scholar] [CrossRef]
- Song, X.; Zhao, Y.; Dykstra, J. Active Damping of Acoustic Ringing Effect for Oil Well Sonic Logging System. IEEE Trans. Ind. Electron. 2017, 64, 3423–3432. [Google Scholar] [CrossRef]
- Ao, Y.; Lu, W.; Hou, Q.; Jiang, B. Synthesize Nuclear Magnetic Resonance T2 Spectrum From Conventional Logging Responses With Spectrum Regression Forest. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1726–1730. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, H.; Zhou, K.; Lin, T. A Design Scheme of Receiving System of Small-Diameter Nuclear Magnetic Resonance Logging Tool. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Bai, Y.; Zhan, Q.; Wang, H.; Chen, T.; He, Q.; Hong, D. Calculation of Tilted Coil Voltage in Cylindrically Multilayered Medium for Well-Logging Applications. IEEE Access 2020, 8, 30081–30091. [Google Scholar] [CrossRef]
- Hu, X.; Fan, Y.; Deng, S.; Yuan, X.; Li, H. Electromagnetic Logging Response in Multilayered Formation with Arbitrary Uniaxially Electrical Anisotropy. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2071–2083. [Google Scholar] [CrossRef]
- Chen, J.; Yue, W.; Li, C.; Zeng, F. Extracting Reflected Waves From Acoustic Logging Data Based on the Shearlet Transform. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1688–1692. [Google Scholar] [CrossRef]
- Aeron, S.; Bose, S.; Valero, H.-P. Robust Detection and Estimation for Logging While Drilling Monopole Acoustic Data. IEEE Trans. Signal Process. 2015, 63, 3062–3075. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, K. Direct Inversion Algorithm for Shear Velocity Profiling in Dipole Acoustic Borehole Measurements. IEEE Geosci. Remote Sens. Lett. 2018, 15, 828–832. [Google Scholar] [CrossRef]
- Gaunkar, N.P.; Nlebedim, I.C.; Bulu, I.; Mina, M.; Hadimani, R.L.; Song, Y.Q.; Jiles, D.C. Broadband Analysis of Response From Magnetic Cores Used in Inductive Sensors for Pulsed Nuclear Magnetic Resonance Applications. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Xu, X.; Kong, X.; Zhang, J.; Wang, G.; Bao, Z.; Yu, H.; Xu, Z. Optimization of Inside-Out Nuclear Magnetic Resonance Sensor with Logging-While-Drilling Tool Specification and Experimental Validation. IEEE Trans. Instrum. Meas. 2022, 71, 1–10. [Google Scholar]
- Lehmensiek, R.; de Villiers, D.-I.-L. Optimization of Log-Periodic Dipole Array Antennas for Wideband Omnidirectional Radiation. IEEE Trans. Antennas Propag. 2015, 63, 3714–3718. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, H.; Huang, W.F.; Xu, W.; Xu, J.; Dai, J.; Liu, Q.H. A Hybrid Loop-Tree FEBI Method for Low-Frequency Well Logging of 3-D Structures in Layered Media. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–9. [Google Scholar]
- Yan, B.; Zhu, W.; Zhuang, X.; Liu, L.; Fang, G. Miniature Three-Axis Induction Magnetometer for Borehole Logging. IEEE Magn. Lett. 2019, 10, 1–4. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, R.; Jin, Y.; Wu, X.; Li, M.; Abubakar, A.; Chen, J. A Supervised Descent Learning Technique for Solving Directional Electromagnetic Logging-While-Drilling Inverse Problems. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8013–8025. [Google Scholar] [CrossRef]
- Yan, L.; Zeng, S.; Chen, J. 2-D Pixel-Based Inversion for Simultaneous Reconstruction of Resistivity and Dielectric Constant From Electromagnetic Logging-While-Drilling Measurements. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar]
- Yan, L.; Jin, Y.; Qi, C.; Yuan, P.; Wang, S.; Wu, X.; Huang, Y.; Chen, J. Deep Learning-Assisted Real-Time Forward Modeling of Electromagnetic Logging in Complex Formations. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Rosa, G.-S.; Bergmann, J.-R.; Teixeira, F.-L. A Perturbation Method to Model Electromagnetic Well-Logging Tools in Curved Boreholes. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1979–1993. [Google Scholar] [CrossRef]
- Xing, G.; Wang, H.; Ding, Z. A New Combined Measurement Method of the Electromagnetic Propagation Resistivity Logging. IEEE Geosci. Remote Sens. Lett. 2008, 5, 430–432. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, L.; Cao, Z. Optimization of the Electromagnetic Wave Resistivity Tool in Logging While Drilling. In Proceedings of the 2013 IEEE International Conference on Imaging Systems and Techniques (IST), Bejing, China, 22–23 October 2013; pp. 160–163. [Google Scholar]
- Liu, X.; Liu, F.; Chen, J.; Zhao, Z.; Wang, A.; Lu, Z. Resistivity Logging Through Casing Response of Inclined Fractured Formation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4919–4929. [Google Scholar] [CrossRef]
- Ren, Y.; Gong, R.; Feng, Z.; Li, M. Valuable data extraction for resistivity imaging logging interpretation. Tsinghua Sci. Technol. 2020, 25, 281–293. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Fan, Y. Bayesian Inversion of Logging-While-Drilling Extra-Deep Directional Resistivity Measurements Using Parallel Tempering Markov Chain Monte Carlo Sampling. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8026–8036. [Google Scholar] [CrossRef]
- Pardo, D.; Torres-Verdin, C.; Demkowicz, L. A 2D and 3D hp-Finite Element Method for Simulation of Through Casing Resistivity Logging Instruments. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 1769–1772. [Google Scholar]
- Available online: https://www.bakerhughes.com/evaluation/wireline-openhole-logging/wireline-imaging/star-imager-service (accessed on 25 June 2022).
- Available online: https://www.halliburton.com/en/products/strataxaminer (accessed on 25 June 2022).
















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Liu, Y.; Li, T.; Yi, S.; Li, N. A Universal Multi-Frequency Micro-Resistivity Array Imaging Method for Subsurface Sensing. Remote Sens. 2022, 14, 3116. https://doi.org/10.3390/rs14133116
Yang H, Liu Y, Li T, Yi S, Li N. A Universal Multi-Frequency Micro-Resistivity Array Imaging Method for Subsurface Sensing. Remote Sensing. 2022; 14(13):3116. https://doi.org/10.3390/rs14133116
Chicago/Turabian StyleYang, Haining, Yuting Liu, Tingjun Li, Shijia Yi, and Na Li. 2022. "A Universal Multi-Frequency Micro-Resistivity Array Imaging Method for Subsurface Sensing" Remote Sensing 14, no. 13: 3116. https://doi.org/10.3390/rs14133116
APA StyleYang, H., Liu, Y., Li, T., Yi, S., & Li, N. (2022). A Universal Multi-Frequency Micro-Resistivity Array Imaging Method for Subsurface Sensing. Remote Sensing, 14(13), 3116. https://doi.org/10.3390/rs14133116