Performance of GEDI Space-Borne LiDAR for Quantifying Structural Variation in the Temperate Forests of South-Eastern Australia
Abstract
:1. Introduction
1.1. Metrics to Estimate Forest Structure Using LiDAR
1.2. The Use of Space-Borne LiDAR Platforms (GEDI) in Remote Sensing of Forests
1.3. Forest Structural Properties
1.4. Aims and Objectives
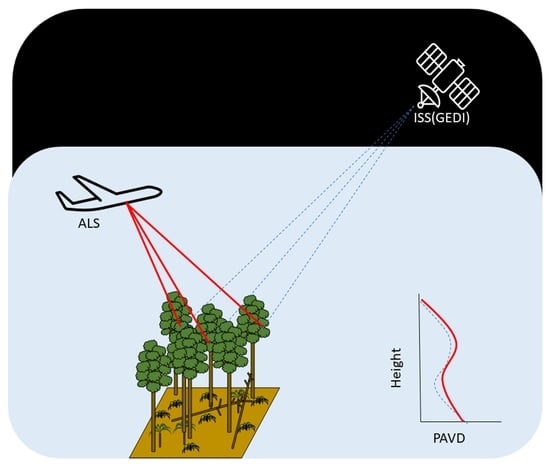
2. Study Area and Data
2.1. Study Area
2.2. Spaceborne LiDAR Dataset
2.3. Airborne LiDAR Data
3. Methodology
3.1. GEDI Data Processing
3.1.1. Elevation and Canopy Height from the Level 2A Data
3.1.2. Total PAI and Vertical Profile Metrics from the Level 2B Data
3.2. ALS Data Processing
3.2.1. Elevation and Slope
3.2.2. Canopy Height
3.2.3. PAI and PAVD Profile
3.3. Comparative Statistical Analysis
3.3.1. Landscape-Level Digital Elevation Model (DEM) Analysis
3.3.2. Landscape-Level Canopy Height and Plant Area Index (PAI) Analysis
3.3.3. Case Study Analysis of PAVD and PAI
4. Results
4.1. DEM Analysis
4.2. Canopy Height
4.2.1. Accuracy of Canopy Height of Individual Footprints
4.2.2. Variation of GEDI Canopy Height Accuracy with Height of the Canopy
4.2.3. Variation of Canopy Height Accuracy with Slope of Terrain
4.3. Plant Area Index
4.3.1. Accuracy of Total PAI of Individual Footprints
4.3.2. Variation of GEDI PAI Accuracy with Height of the Canopy
4.3.3. Variation of PAI Accuracy with Slope of Terrain
4.4. Analysis of Two Forest Age Classes
5. Discussion
5.1. Ground Elevation Effect on Height and Density Attributes
5.2. Can GEDI Estimate ALS-Based Canopy Height?
5.3. Can GEDI Estimate Total PAI Accurately?
5.4. Can GEDI Represent the Vertical Canopy Profile Accurately?
5.5. Operational Use of GEDI in South-East Australian Forests
5.6. Limitations of the Study
5.7. Future Research
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lefsky, M.A.; Cohen, W.B.; Acker, S.A.; Parker, G.G.; Spies, T.A.; Harding, D. Lidar Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests. Remote Sens. Environ. 1999, 70, 339–361. [Google Scholar] [CrossRef]
- Riaño, D.; Valladares, F.; Condés, S.; Chuvieco, E. Estimation of Leaf Area Index and Covered Ground from Airborne Laser Scanner (Lidar) in Two Contrasting Forests. Agric. For. Meteorol. 2004, 124, 269–275. [Google Scholar] [CrossRef]
- Shugart, H.H.; Saatchi, S.; Hall, F.G. Importance of Structure and Its Measurement in Quantifying Function of Forest Ecosystems. J. Geophys. Res. Biogeosci. 2010, 115, G00E13. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A Review of Radar Remote Sensing for Biomass Estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef] [Green Version]
- Naesset, E. Determination of Mean Tree Height of Forest Stands Using Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1997, 52, 49–56. [Google Scholar] [CrossRef]
- Nilsson, M. Estimation of Tree Heights and Stand Volume Using an Airborne Lidar System. Remote Sens. Environ. 1996, 56, 1–7. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface Lidar Remote Sensing of Basal Area and Biomass in Deciduous Forests of Eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Lefsky, M.A. Application of Lidar Remote Sensing to the Estimation of Forest Canopy and Stand Structure. Ph.D. Thesis, University of Virginia, Charlottesville, VA, USA, 1997. Volume 130. [Google Scholar]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito-Santo, F.; Hunter, M.O.; de Oliveira, R., Jr. Estimates of Forest Canopy Height and Aboveground Biomass Using ICESat. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies: Lidar, an Emerging Remote Sensing Technology That Directly Measures the Three-Dimensional Distribution of Plant Canopies, Can Accurately Estimate Vegetation Structural Attributes and Should Be of Particular Inte. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Magnussen, S.; Boudewyn, P. Derivations of Stand Heights from Airborne Laser Scanner Data with Canopy-Based Quantile Estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
- Jaskierniak, D.; Lucieer, A.; Kuczera, G.; Turner, D.; Lane, P.N.J.; Benyon, R.G.; Haydon, S. Individual Tree Detection and Crown Delineation from Unmanned Aircraft System (UAS) LiDAR in Structurally Complex Mixed Species Eucalypt Forests. ISPRS J. Photogramm. Remote Sens. 2021, 171, 171–187. [Google Scholar] [CrossRef]
- McColl-Gausden, S.C.; Bennett, L.T.; Clarke, H.G.; Ababei, D.A.; Penman, T.D. The Fuel–Climate–Fire Conundrum: How Will Fire Regimes Change in Temperate Eucalypt Forests under Climate Change? Glob. Chang. Biol. 2022. [Google Scholar] [CrossRef]
- Keeley, J.E.; Syphard, A.D. Climate Change and Future Fire Regimes: Examples from California. Geosciences 2016, 6, 37. [Google Scholar] [CrossRef] [Green Version]
- Cary, G.J. Importance of a Changing Climate for Fire Regimes in Australia. In Flammable Australia: The Fire Regimes and Biodiversity of a Continent; Bradstock, R.A., Williams, J.E., Gill, M.A., Eds.; Cambridge University Press: Cambridge, UK, 2002; pp. 26–46. [Google Scholar]
- Liu, Z.; Wimberly, M.C. Direct and Indirect Effects of Climate Change on Projected Future Fire Regimes in the Western United States. Sci. Total Environ. 2016, 542, 65–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goetz, S.; Dubayah, R. Advances in Remote Sensing Technology and Implications for Measuring and Monitoring Forest Carbon Stocks and Change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Bustamante, M.M.C.; Roitman, I.; Aide, T.M.; Alencar, A.; Anderson, L.O.; Aragão, L.; Asner, G.P.; Barlow, J.; Berenguer, E.; Chambers, J. Toward an Integrated Monitoring Framework to Assess the Effects of Tropical Forest Degradation and Recovery on Carbon Stocks and Biodiversity. Glob. Chang. Biol. 2016, 22, 92–109. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P. Tropical Forest Carbon Assessment: Integrating Satellite and Airborne Mapping Approaches. Environ. Res. Lett. 2009, 4, 34009. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-Resolution Laser Ranging of the Earth’s Forests and Topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Hall, F.G.; Bergen, K.; Blair, J.B.; Dubayah, R.; Houghton, R.; Hurtt, G.; Kellndorfer, J.; Lefsky, M.; Ranson, J.; Saatchi, S. Characterizing 3D Vegetation Structure from Space: Mission Requirements. Remote Sens. Environ. 2011, 115, 2753–2775. [Google Scholar] [CrossRef] [Green Version]
- Bergen, K.M.; Goetz, S.J.; Dubayah, R.O.; Henebry, G.M.; Hunsaker, C.T.; Imhoff, M.L.; Nelson, R.F.; Parker, G.G.; Radeloff, V.C. Remote Sensing of Vegetation 3-D Structure for Biodiversity and Habitat: Review and Implications for Lidar and Radar Spaceborne Missions. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Aber, J.D. Foliage-height Profiles and Succession in Northern Hardwood Forests. Ecology 1979, 60, 18–23. [Google Scholar] [CrossRef]
- Gower, S.T.; Norman, J.M. Rapid Estimation of Leaf Area Index in Conifer and Broad-Leaf Plantations. Ecology 1991, 72, 1896–1900. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR Essential Climate Variables and FCOVER Global Time Series Capitalizing over Existing Products. Part1: Principles of Development and Production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.A.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating Canopy Structure of Douglas-Fir Forest Stands from Discrete-Return LiDAR. Trees Struct. Funct. 2007, 21, 295–310. [Google Scholar] [CrossRef] [Green Version]
- Jaskierniak, D.; Lane, P.N.J.; Robinson, A.; Lucieer, A. Extracting LiDAR Indices to Characterise Multilayered Forest Structure Using Mixture Distribution Functions. Remote Sens. Environ. 2011, 115, 573–585. [Google Scholar] [CrossRef]
- Mitchell, P.J.; Benyon, R.G.; Lane, P.N.J. Responses of Evapotranspiration at Different Topographic Positions and Catchment Water Balance Following a Pronounced Drought in a Mixed Species Eucalypt Forest, Australia. J. Hydrol. 2012, 440–441, 62–74. [Google Scholar] [CrossRef]
- Fedrigo, M.; Newnham, G.J.; Coops, N.C.; Culvenor, D.S.; Bolton, D.K.; Nitschke, C.R. Predicting Temperate Forest Stand Types Using Only Structural Profiles from Discrete Return Airborne Lidar. ISPRS J. Photogramm. Remote Sens. 2018, 136, 106–119. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J. Fusing Simulated GEDI, ICESat-2 and NISAR Data for Regional Aboveground Biomass Mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural Network Guided Interpolation for Mapping Canopy Height of China’s Forests by Integrating GEDI and ICESat-2 Data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised Method for Forest Canopy Height Estimation from Geoscience Laser Altimeter System Waveforms. J. Appl. Remote Sens. 2007, 1, 13537. [Google Scholar]
- Qi, W.; Dubayah, R.O. Combining Tandem-X InSAR and Simulated GEDI Lidar Observations for Forest Structure Mapping. Remote Sens. Environ. 2016, 187, 253–266. [Google Scholar] [CrossRef]
- Spracklen, B.; Spracklen, D. V Determination of Structural Characteristics of Old-Growth Forest in Ukraine Using Spaceborne LiDAR. Remote Sens. 2021, 13, 1233. [Google Scholar] [CrossRef]
- Rishmawi, K.; Huang, C.; Zhan, X. Monitoring Key Forest Structure Attributes across the Conterminous United States by Integrating GEDI LiDAR Measurements and VIIRS Data. Remote Sens. 2021, 13, 442. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-Resolution Mapping of Forest Canopy Height Using Machine Learning by Coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 Data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest Canopy Height in Northern China by Synergizing ICESat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance Evaluation of GEDI and ICESat-2 Laser Altimeter Data for Terrain and Canopy Height Retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Pascual, A. Using GEDI Lidar Data and Airborne Laser Scanning to Assess Height Growth Dynamics in Fast-Growing Species: A Showcase in Spain. For. Ecosyst. 2021, 8, 14. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Huettermann, S.; Jones, S.; Soto-Berelov, M.; Hislop, S. Intercomparison of Real and Simulated GEDI Observations across Sclerophyll Forests. Remote Sens. 2022, 14, 2096. [Google Scholar] [CrossRef]
- Nyman, P.; Metzen, D.; Hawthorne, S.N.D.; Duff, T.J.; Inbar, A.; Lane, P.N.J.; Sheridan, G.J. Evaluating Models of Shortwave Radiation below Eucalyptus Canopies in SE Australia. Agric. For. Meteorol. 2017, 246, 51–63. [Google Scholar] [CrossRef]
- Brown, T.P.; Inbar, A.; Duff, T.J.; Burton, J.; Noske, P.J.; Lane, P.N.J.; Sheridan, G.J. Forest Structure Drives Fuel Moisture Response across Alternative Forest States. Fire 2021, 4, 48. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Haywood, A.; Skidmore, A.K. Mapping Forest Canopy Height across Large Areas by Upscaling ALS Estimates with Freely Available Satellite Data. Remote Sens. 2015, 7, 12563–12587. [Google Scholar] [CrossRef] [Green Version]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR Remote Sensing of Forest Structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Monsi, M.; Saeki, T. On the Factor Light in Plant Communities and Its Importance for Matter Production. Ann. Bot. 2005, 95, 549. [Google Scholar] [CrossRef] [Green Version]
- Cawson, J.G.; Duff, T.J.; Tolhurst, K.G.; Baillie, C.C.; Penman, T.D. Fuel Moisture in Mountain Ash Forests with Contrasting Fire Histories. For. Ecol. Manag. 2017, 400, 568–577. [Google Scholar] [CrossRef]
- Edwards, D.P.; Fisher, B.; Boyd, E. Protecting Degraded Rainforests: Enhancement of Forest Carbon Stocks under REDD+. Conserv. Lett. 2010, 3, 313–316. [Google Scholar] [CrossRef]
- Griebel, A.; Bennett, L.T.; Culvenor, D.S.; Newnham, G.J.; Arndt, S.K. Reliability and Limitations of a Novel Terrestrial Laser Scanner for Daily Monitoring of Forest Canopy Dynamics. Remote Sens. Environ. 2015, 166, 205–213. [Google Scholar] [CrossRef]
- Karna, K.Y.; Penman, D.T.; Aponte, C.; Bennett, T.L. Assessing Legacy Effects of Wildfires on the Crown Structure of Fire-Tolerant Eucalypt Trees Using Airborne LiDAR Data. Remote Sens. 2019, 11, 2433. [Google Scholar] [CrossRef] [Green Version]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Haywood, A.; Mellor, A.; Woodgate, W.; Soto-Berelov, M.; Skidmore, A.K. Using Discrete-Return Airborne Laser Scanning to Quantify Number of Canopy Strata across Diverse Forest Types. Methods Ecol. Evol. 2016, 7, 700–712. [Google Scholar] [CrossRef]
- Woodgate, W.; Disney, M.; Armston, J.D.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M.; Haywood, A.; Mellor, A. An Improved Theoretical Model of Canopy Gap Probability for Leaf Area Index Estimation in Woody Ecosystems. For. Ecol. Manag. 2015, 358, 303–320. [Google Scholar] [CrossRef]
- Wilkes, P.; Jones, S.D.; Suarez, L.; Haywood, A.; Woodgate, W.; Soto-Berelov, M.; Mellor, A.; Skidmore, A.K. Understanding the Effects of ALS Pulse Density for Metric Retrieval across Diverse Forest Types. Photogramm. Eng. Remote Sens. 2015, 81, 625–635. [Google Scholar] [CrossRef]
- Tang, H.; Armston, J.; Dubayah, R. Algorithm Theoretical Basis Document (ATBD) for GEDI L2B Footprint Canopy Cover and Vertical Profile Metrics; Goddard Space Flight Center: Greenbelt, MD, USA, 2019. [Google Scholar]
- Hofton, M.; Blair, J.B.; Story, S.; Yi, D. Algorithm Theoretical Basis Document (ATBD) for GEDI Transmit and Receive Waveform Processing for L1 and L2 Products; University of Maryland: College Park, MA, USA, 2020. [Google Scholar]
- Ni-Meister, W.; Jupp, D.L.B.; Dubayah, R. Modeling Lidar Waveforms in Heterogeneous and Discrete Canopies. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1943–1958. [Google Scholar] [CrossRef] [Green Version]
- Armston, J.; Disney, M.; Lewis, P.; Scarth, P.; Phinn, S.; Lucas, R.; Bunting, P.; Goodwin, N. Direct Retrieval of Canopy Gap Probability Using Airborne Waveform Lidar. Remote Sens. Environ. 2013, 134, 24–38. [Google Scholar] [CrossRef]
- Pisek, J.; Govind, A.; Arndt, S.K.; Hocking, D.; Wardlaw, T.J.; Fang, H.; Matteucci, G.; Longdoz, B. Intercomparison of Clumping Index Estimates from POLDER, MODIS, and MISR Satellite Data over Reference Sites. ISPRS J. Photogramm. Remote Sens. 2015, 101, 47–56. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Swatantran, A.; Hofton, M.; Sheldon, S.; Clark, D.B.; Blair, B. Retrieval of Vertical LAI Profiles over Tropical Rain Forests Using Waveform Lidar at La Selva, Costa Rica. Remote Sens. Environ. 2012, 124, 242–250. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S. Lidar-Based Mapping of Leaf Area Index and Its Use for Validating GLOBCARBON Satellite LAI Product in a Temperate Forest of the Southern USA. Remote Sens. Environ. 2009, 113, 1628–1645. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; Coops, N.C.; Tompalski, P.; Goodbody, T.R.H.; Meador, A.S.; Bourdon, J.-F.; de Boissieu, F.; Achim, A. LidR: An R Package for Analysis of Airborne Laser Scanning (ALS) Data. Remote Sens. Environ. 2020, 251, 112061. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing; Team R C: Vienna, Austria, 2021.
- Silva, C.A.; Saatchi, S.; Garcia, M.; Labriere, N.; Klauberg, C.; Ferraz, A.; Meyer, V.; Jeffery, K.J.; Abernethy, K.; White, L. Comparison of Small-and Large-Footprint Lidar Characterization of Tropical Forest Aboveground Structure and Biomass: A Case Study from Central Gabon. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3512–3526. [Google Scholar] [CrossRef] [Green Version]
- Silva, C.A.; Hamamura, C.; Valbuena, R.; Hancock, S.; Cardil, A.; Broadbent, E.N.; Almeida, D.R.A.; Silva Junior, C.H.L.; Klauberg, C. RGEDI: NASA’s Global Ecosystem Dynamics Investigation (GEDI) Data Visualization and Processing 2020. Available online: https://cran.microsoft.com/snapshot/2020-04-20/web/packages/rGEDI/vignettes/tutorial.html (accessed on 17 May 2022).
- Roy, D.P.; Kashongwe, H.B.; Armston, J. The Impact of Geolocation Uncertainty on GEDI Tropical Forest Canopy Height Estimation and Change Monitoring. Sci. Remote Sens. 2021, 4, 100024. [Google Scholar] [CrossRef]
- Lovell, J.L.; Jupp, D.L.B.; Culvenor, D.S.; Coops, N.C. Using Airborne and Ground-Based Ranging Lidar to Measure Canopy Structure in Australian Forests. Can. J. Remote Sens. 2003, 29, 607–622. [Google Scholar] [CrossRef]
- Riaño, D.; Meier, E.; Allgöwer, B.; Chuvieco, E.; Ustin, S.L. Modeling Airborne Laser Scanning Data for the Spatial Generation of Critical Forest Parameters in Fire Behavior Modeling. Remote Sens. Environ. 2003, 86, 177–186. [Google Scholar] [CrossRef]
- Wilkes, P. ForestLAS, A Package for Reading, Writing and Analysing ALS Point Data for Forestry Applications. Available online: https://bitbucket.org/phil_wilkes/forestlas/src/master/ (accessed on 14 September 2021).
- Fairman, T.A.; Nitschke, C.R.; Bennett, L.T. Too Much, Too Soon? A Review of the Effects of Increasing Wildfire Frequency on Tree Mortality and Regeneration in Temperate Eucalypt Forests. Int. J. Wildl. Fire 2016, 25, 831–848. [Google Scholar] [CrossRef]
- Nolan, R.H.; Lane, P.N.J.; Benyon, R.G.; Bradstock, R.A.; Mitchell, P.J. Trends in Evapotranspiration and Streamflow Following Wildfire in Resprouting Eucalypt Forests. J. Hydrol. 2015, 524, 614–624. [Google Scholar] [CrossRef]
- Lakmali, S.; Benyon, R.G.; Sheridan, G.J.; Lane, P.N.J. Change in Fire Frequency Drives a Shift in Species Composition in Native Eucalyptus Regnans Forests: Implications for Overstorey Forest Structure and Transpiration. Ecohydrology 2022, 15, e2412. [Google Scholar] [CrossRef]
- Mitchell, P.; Lane, P.; Benyon, R. Capturing within Catchment Variation in Evapotranspiration from Montane Forests Using LiDAR Canopy Profiles with Measured and Modelled Fluxes of Water. Ecohydrology 2012, 5, 708–720. [Google Scholar] [CrossRef]
- Taylor, C.; Blair, D.; Keith, H.; Lindenmayer, D. Resource Conflict across Melbourne’s Largest Domestic Water Supply Catchment; The Australian National University, Fenner School of Environment and Society: Canberra, Australia, 2018. [Google Scholar]
- Mannik, R.D.; Herron, A.; Hill, P.I.; Brown, R.E.; Moran, R. Estimating the Change in Streamflow Resulting from the 2003 and 2006/2007 Bushfires in Southeastern Australia. Australas. J. Water Resour. 2013, 16, 107–120. [Google Scholar] [CrossRef]
- Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-Evaluation of Forest Biomass Carbon Stocks and Lessons from the World’s Most Carbon-Dense Forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burns, E.; Lowe, A.; Lindenmayer, D.; Thurgate, N. Biodiversity and Environmental Change: Monitoring, Challenges and Direction; CSIRO Publishing: Victoria, BC, Canada, 2014; ISBN 0643108572. [Google Scholar]
- Wang, C.; Elmore, A.J.; Numata, I.; Cochrane, M.A.; Shaogang, L.; Huang, J.; Zhao, Y.; Li, Y. Factors Affecting Relative Height and Ground Elevation Estimations of GEDI among Forest Types across the Conterminous USA. GIScience Remote Sens. 2022, 59, 975–999. [Google Scholar] [CrossRef]
- Quirós, E.; Polo, M.-E.; Fragoso-Campón, L. GEDI Elevation Accuracy Assessment: A Case Study of Southwest Spain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5285–5299. [Google Scholar] [CrossRef]
- Trouvé, R.; Nitschke, C.R.; Robinson, A.P.; Baker, P.J. Estimating the Self-Thinning Line from Mortality Data. For. Ecol. Manag. 2017, 402, 122–134. [Google Scholar] [CrossRef]
- Kutchartt, E.; Pedron, M.; Pirotti, F. Assessment of Canopy and Ground Height Accuracy from Gedi Lidar over Steep Mountain Areas. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, V-3-2022, 431–438. [Google Scholar] [CrossRef]
- Ashton, D.H. The Development of Even-Aged Stands of Eucalyptus Regnans F. Muell. in Central Victoria. Aust. J. Bot. 1976, 24, 397–414. [Google Scholar] [CrossRef]
- Jaskierniak, D.; Kuczera, G.; Benyon, R.G.; Haydon, S.; Lane, P.N.J. Top-down Seasonal Streamflow Model with Spatiotemporal Forest Sapwood Area. J. Hydrol. 2019, 568, 372–384. [Google Scholar] [CrossRef]
- Qi, W.; Saarela, S.; Armston, J.; Ståhl, G.; Dubayah, R. Forest Biomass Estimation over Three Distinct Forest Types Using TanDEM-X InSAR Data and Simulated GEDI Lidar Data. Remote Sens. Environ. 2019, 232, 111283. [Google Scholar] [CrossRef]









| Platform: | International Space Station |
|---|---|
| Coverage Extent: | Between 51.6 N and S Latitude |
| File numbers of the two GEDI tracks used: |
|
| Date and time of acquisition of the two tracks: | 20 July 2019 and 14 August 2019 |
| Footprint size: | ~25 m diameter |
| Along-track spacing: | 60 m |
| Across-track spacing: | 600 m |
| Swath width: | 4.2 km |
| Beams used: | 4 power beams and 4 coverage beams |
| Title of Project: | 2015–2016 Central Highlands LiDAR Project |
|---|---|
| Purpose: | To map the key forest structure |
| Coverage extent: | 4580 km2 northeast of Melbourne in Victoria |
| Date of acquisition: | January to May 2016 |
| Sensor Name: | Trimble AX60 |
| Avg. Point Density: | 4.38 pts/m2 |
| Nominal density: | 4 outgoing laser pulses per square meter with 50% overlap in swaths |
| Footprint Size: | 0.22 m diameter |
| Number of returns: | Up to 7 returns |
| Data Format: | LAS 1.3, Waveform Packets |
| Beam Type | Median | MAD | Mean | MAE | MAPE (%) | RMSE | RMSPE (%) | Bias | %Bias (%) | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Power | −2.03 | 5.19 | −0.75 | 6.69 | 29.79 | 10.29 | 76.97 | −0.75 | −12.51 | 0.63 |
| Coverage | −1.67 | 5.58 | 1.57 | 7.58 | 30.50 | 11.92 | 58.00 | 1.57 | −6.24 | 0.51 |
| Both | −1.88 | 5.35 | 0.18 | 7.05 | 30.08 | 10.97 | 70.02 | 0.18 | −10.01 | 0.58 |
| Height Bin (m) | Median | MAD | Mean | MAE | MAPE (%) | RMSE | RMSPE (%) |
|---|---|---|---|---|---|---|---|
| 0–10 | −5.79 | 4.87 | -7.31 | 7.73 | 151.31 | 10.43 | 256.58 |
| 10–20 | −3.83 | 5.68 | -3.74 | 6.40 | 45.31 | 7.74 | 61.45 |
| 20–30 | −1.98 | 5.63 | -0.83 | 6.11 | 24.31 | 8.28 | 33.12 |
| 30–40 | −1.40 | 5.47 | 1.41 | 7.34 | 21.02 | 10.54 | 30.23 |
| 40–50 | −1.46 | 5.17 | 2.41 | 8.02 | 18.02 | 12.64 | 28.88 |
| 50–60 | −1.16 | 4.05 | 2.06 | 6.87 | 12.67 | 12.66 | 23.59 |
| >60 | 0.03 | 4.17 | 3.77 | 6.90 | 10.73 | 14.16 | 22.72 |
| Slope Bin (Degree) | Median | MAD | Mean | MAE | MAPE (%) | RMSE | RMSPE (%) |
|---|---|---|---|---|---|---|---|
| 0–5 | −1.13 | 3.96 | 0.75 | 5.62 | 25.07 | 9.66 | 67.56 |
| 5–10 | −1.38 | 4.11 | 0.41 | 5.91 | 27.13 | 9.93 | 63.42 |
| 10–15 | −1.53 | 4.94 | 0.97 | 6.88 | 29.88 | 11.13 | 72.81 |
| 15–20 | −1.85 | 5.69 | 1.08 | 7.75 | 32.13 | 12.04 | 70.02 |
| 20–25 | −2.56 | 5.86 | −0.46 | 7.45 | 31.81 | 11.18 | 70.60 |
| 25–30 | −2.89 | 6.23 | −0.52 | 7.81 | 31.54 | 11.16 | 58.26 |
| 30–35 | −3.84 | 6.55 | −2.42 | 7.67 | 33.70 | 10.39 | 101.23 |
| 35–40 | −4.09 | 6.48 | −2.41 | 8.23 | 30.41 | 11.26 | 51.24 |
| 40–50 | −4.22 | 7.67 | −1.75 | 9.36 | 28.76 | 13.31 | 39.51 |
| 50–60 | −11.11 | 3.48 | −8.04 | 10.70 | 27.29 | 11.27 | 29.20 |
| Beam Type | Median | MAD | Mean | MAE | MAPE (%) | RMSE | RMSPE (%) | Bias | %Bias (%) | R2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Power | −0.44 | 0.70 | −0.73 | 0.85 | 131.16 | 1.23 | 337.27 | −0.73 | −115.52 | 0.15 |
| Coverage | −0.73 | 0.83 | −0.85 | 0.92 | 163.49 | 1.17 | 444.19 | −0.85 | −154.09 | 0.20 |
| Both | −0.55 | 0.78 | −0.78 | 0.88 | 144.08 | 1.21 | 383.60 | −0.78 | −130.94 | 0.17 |
| Height Bin (m) | Median | MAD | Mean | MAE | MAPE | RMSE | RMSPE |
|---|---|---|---|---|---|---|---|
| 0–10 | −0.56 | 0.82 | −0.94 | 1.00 | 659.82 | 1.42 | 1441.78 |
| 10–20 | −0.44 | 0.75 | −0.76 | 0.85 | 163.35 | 1.24 | 310.41 |
| 20–30 | −0.51 | 0.73 | −0.76 | 0.85 | 131.61 | 1.19 | 275.95 |
| 30–40 | −0.66 | 0.82 | −0.88 | 0.95 | 126.73 | 1.27 | 230.07 |
| 40–50 | −0.59 | 0.79 | −0.77 | 0.88 | 98.76 | 1.18 | 154.92 |
| 50–60 | −0.49 | 0.71 | −0.69 | 0.81 | 83.98 | 1.11 | 125.41 |
| >60 | −0.39 | 0.69 | −0.55 | 0.71 | 67.88 | 0.98 | 96.38 |
| Slope Bin (Degree) | Median | MAD | Mean | MAE | MAPE | RMSE | RMSPE |
|---|---|---|---|---|---|---|---|
| 0–5 | −0.32 | 0.47 | −0.42 | 0.53 | 84.41 | 0.76 | 216.85 |
| 5–10 | −0.35 | 0.53 | −0.49 | 0.59 | 92.58 | 0.84 | 247.88 |
| 10–15 | −0.41 | 0.63 | −0.61 | 0.72 | 117.38 | 1.01 | 323.07 |
| 15–20 | −0.55 | 0.80 | −0.77 | 0.88 | 150.17 | 1.22 | 382.80 |
| 20–25 | −0.80 | 0.99 | −0.96 | 1.04 | 170.24 | 1.35 | 483.25 |
| 25–30 | −1.02 | 1.09 | −1.13 | 1.21 | 202.79 | 1.52 | 456.01 |
| 30–35 | −1.22 | 1.15 | −1.31 | 1.36 | 236.16 | 1.67 | 618.52 |
| 35–40 | −1.46 | 1.17 | −1.43 | 1.50 | 220.22 | 1.78 | 316.29 |
| 40–50 | −1.36 | 1.12 | −1.42 | 1.47 | 211.05 | 1.76 | 304.31 |
| 50–60 | −2.14 | 0.13 | −1.72 | 1.72 | 194.17 | 1.90 | 217.77 |
| Fire Age-Class | 1939 | 2009 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Height Bin (m) | Median | MAD | MAE | MAPE | RMSE | RMSPE | Median | MAD | MAE | MAPE | RMSE | RMSPE |
| 5 | 0.012 | 0.077 | 0.068 | 88.30 | 0.088 | 144.04 | −0.007 | 0.097 | 0.089 | 747.57 | 0.121 | 4617.36 |
| 10 | −0.026 | 0.035 | 0.046 | 11,246.96 | 0.067 | 133,410.21 | −0.038 | 0.071 | 0.075 | 505.67 | 0.104 | 1676.06 |
| 15 | −0.008 | 0.016 | 0.020 | 7043.90 | 0.029 | 93,788.13 | −0.042 | 0.039 | 0.052 | 1254.64 | 0.066 | 3678.82 |
| 20 | −0.004 | 0.010 | 0.012 | 5779.06 | 0.019 | 87,236.17 | −0.011 | 0.019 | 0.028 | 1250.35 | 0.042 | 3897.17 |
| 25 | −0.001 | 0.008 | 0.010 | 1171.97 | 0.02 | 17,616.88 | 0.000 | 0.007 | 0.015 | 622.60 | 0.03 | 2749.55 |
| 30 | −0.001 | 0.009 | 0.010 | 103.61 | 0.017 | 416.49 | 0.003 | 0.003 | 0.012 | 111.23 | 0.027 | 177.57 |
| 40 | −0.002 | 0.012 | 0.012 | 67.83 | 0.016 | 131.91 | 0.004 | 0.002 | 0.009 | 94.94 | 0.022 | 96.66 |
| 50 | 0.003 | 0.015 | 0.013 | 42.99 | 0.017 | 74.02 | 0.003 | 0.001 | 0.005 | 94.85 | 0.009 | 0.96 |
| 60 | 0.002 | 0.015 | 0.014 | 65.82 | 0.019 | 97.43 | - | - | - | - | - | - |
| 70 | 0.001 | 0.010 | 0.008 | 61.66 | 0.011 | 70.87 | - | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhargay, S.; Lyell, C.S.; Brown, T.P.; Inbar, A.; Sheridan, G.J.; Lane, P.N.J. Performance of GEDI Space-Borne LiDAR for Quantifying Structural Variation in the Temperate Forests of South-Eastern Australia. Remote Sens. 2022, 14, 3615. https://doi.org/10.3390/rs14153615
Dhargay S, Lyell CS, Brown TP, Inbar A, Sheridan GJ, Lane PNJ. Performance of GEDI Space-Borne LiDAR for Quantifying Structural Variation in the Temperate Forests of South-Eastern Australia. Remote Sensing. 2022; 14(15):3615. https://doi.org/10.3390/rs14153615
Chicago/Turabian StyleDhargay, Sonam, Christopher S. Lyell, Tegan P. Brown, Assaf Inbar, Gary J. Sheridan, and Patrick N. J. Lane. 2022. "Performance of GEDI Space-Borne LiDAR for Quantifying Structural Variation in the Temperate Forests of South-Eastern Australia" Remote Sensing 14, no. 15: 3615. https://doi.org/10.3390/rs14153615
APA StyleDhargay, S., Lyell, C. S., Brown, T. P., Inbar, A., Sheridan, G. J., & Lane, P. N. J. (2022). Performance of GEDI Space-Borne LiDAR for Quantifying Structural Variation in the Temperate Forests of South-Eastern Australia. Remote Sensing, 14(15), 3615. https://doi.org/10.3390/rs14153615