1. Introduction
Hyperbolic diffractions in Ground Penetrating Radar (GPR) data are caused by a variety of subsurface objects such as pipes, cables, stones, or archaeological artifacts. The spatial distribution of their apex points can aid to investigate the spatial distribution of these subsurface structures. Additional information derivable from the hyperbola is the propagation velocity of electromagnetic waves in the subsurface, which is needed to determine the depth of the objects and/or the 3D-distribution of the water content of the soil.
With the advent of multi-channel GPR antenna arrays, it has become easy to cover large areas in short time with high spatial sampling, i.e., inline and crossline trace distances of 4 and 8 cm, respectively [
1]. This leads to large data volumes, from which often only a small portion of information is taken out for interpretation. On the one hand, for some applications this is sufficient, e.g., for delineating structures in timeslices such as pipes or rebar. On the other hand, this limited output of information is also due to high costs and time in experienced manpower to inspect the data carefully in all aspects. However, the latter can be supported by machine learning algorithms that became widely used in the last decades and have also been used in the context of GPR processing to automatically detect pipes or rebar [
2,
3,
4,
5,
6,
7,
8], defects in concrete [
9], tree roots [
10,
11,
12], and in radargrams or archaic hearths in timeslices [
13].
Most articles on hyperbola detection use a two-step approach or focus just on one of the steps. The first step is to detect the hyperbola in the radargram (spatial coordinate and traveltime) and the second step is to derive information such as the velocity or radius of the pipe from its shape. Whereas this procedure is easily applied to the detection of, e.g., pipes in urban environments, where radargrams are often relatively clear and simple, examples with applications to archaeology in a rather natural environment are missing. This might be because a straight line of hyperbola detected on parallel profiles is easy to connect to a pipe, but archaeological objects causing diffractions are not necessarily in line. In addition, pipes in urban environments are located in a relatively homogeneous background, whereas the subsurface of archaeological sites can be very heterogeneous and thus show complicated radargrams.
The automatic detection of hyperbolas in radargrams can be accomplished with artificial neural networks, where the radargram is seen as an image. Object detection in images is widely conducted using machine learning and deep learning [
14]. Often used networks in the context of object detection in images are R-CNN (regions with convolutional neural network) [
15], Faster R-CNN [
16], Cascade R-CNN [
17], SSD (Single shot multibox detector) [
18], YOLO (You Only Look Once) [
19,
20], or RetinaNet [
21,
22] to name just a few. The architecture of these networks can be built in deep learning frameworks such as pytorch, keras, or Matlab’s Deep Learning toolbox. To avoid the large number of images required for training, they can also be used as pretrained models in transfer learning to be adapted to the specific problem, which in our case is the detection of hyperbola in radargrams.
Probably the first paper using a simple artificial neural network in order to detect hyperbolas in radargrams was by the authors of ref. [
2]. They fed a binary image of the radargram into a neural network with two layers and received the apex points of the hyperbola. Since about the year 2010, the number of articles using neural networks for apex detection has increased. Ref. [
23] used a neural network of four layers with trapezoidal shaped images of hyperbola as training images. Unfortunately, no specific evaluation of the number of well- and misclassified hyperbola was provided. Since the advent of convolutional neural network (CNN) for object detection and classification in images [
14], some of the above mentioned common deep convolutional networks have also been applied to radargrams and the detection of hyperbola, e.g., refs. [
6,
8,
9,
24,
25].
One group of these networks is called region-based convolutional neural networks (R-CNN) [
15] and has gained increased speed over time (Fast and Faster R-CNN [
16,
26]). Faster R-CNN uses a CNN first in order to generate feature maps of the input image. Then, a region proposal network (RPN) is applied on the feature maps, which is again a CNN with some more layers, in order to propose regions in the image that are likely to contain objects. In a last step, the proposed regions are fed into another neural network with fully connected layers in order to extract bounding box coordinates and a classification of the object. The bounding box coordinates are the pixel-based coordinates of a box around the object in the original image. Faster R-CNN has been used for hyperbola detection by, e.g., refs. [
6,
8,
24].
A different network design has the YOLO (You Only Look Once) [
19,
20] object detector and its enhancements (up to YOLOv5). It also uses a deep CNN, but the input image is split into an S × S grid and for each of the grid cells a classification and bounding box regression is determined, which are combined in the end into final detections. This one-stage procedure has the advantage of being faster than the two-stage R-CNN detectors mentioned above. YOLOv5 was used by ref. [
9] for detecting internal defects in asphalt from GPR data.
Once a hyperbola is detected, its shape can be used to determine the propagation velocity of electromagnetic waves. The mostly mentioned method to derive the velocity from the shape of the hyperbola is the Hough transform [
27,
28,
29,
30,
31,
32,
33], which is a computationally intensive gridsearch. Another approach is the fitting of detected points on the hyperbolic signature with orthogonal distance fitting [
34] or the Random Sample Consensus (RANSAC) [
35].
In all the articles mentioned above, the comparison between automatically determined hyperbola parameters (which are in a reasonable range) and the ones manually derived by an experienced operator are missing. So how correct is the automatic determination, and what do these hyperbola parameters tell us? Obviously, the horizontal apex location provides the horizontal location of the scattering object, e.g., the pipe, rebar, root, or stone. The derived propagation velocity can be used to calculate the depth of the object from the traveltime to the apex. In case studies dealing with the urban detection of pipes or rebar, this is sufficient to delineate the underground infrastructure. However, what if the hyperbola originates from single stones or objects spread across an archaeological site? Conducting a multichannel GPR survey with small profile spacing across a single stone will result in diffraction hyperbola on several neighboring channels, i.e., the diffraction pattern is a hyperboloid in 3D. They will reveal the same velocity, but obviously have different apex locations on the neighboring radargrams, although they originate from one object. In addition, the subsurface on archaeological sites is mostly very heterogeneous compared with concrete bridge decks or asphalt in urban environments. Thus, we can expect heterogeneous radargrams with overlapping structures that mask the hyperbola.
So the questions that arise are:
How effective and accurate is the use of an artificial neural network (RetinaNet in our case) in order to automatically detect hyperbola on large scale multi-channel GPR data measured on an archaeological site?
Which fitting method for velocity determination is best and how accurate is the velocity determination compared to manual interpretation?
To answer these questions, we used a Malå MIRA (Mala Imaging Radar) GPR dataset collected using 16 channels measured on the archaeological site of Goting on the island of Föhr in Northern Germany. This site yields a stratified settlement with occupation phases ranging from the Younger Roman Iron Age to the High Medieval Period. In the area selected for measurements, prior magnetic survey and archaeological excavations have revealed divided areas used for residential and artisanal, harbor-related activities during the Early Medieval Period (8th–11th century AD), including cultural layers, workshop spaces, sunken-feature buildings, wells, and numerous ditches, forming parcellations and yard divisions [
36,
37,
38]. The radargrams show a variety of archaeological features such as pits and dipping layers, but also a lot of diffraction hyperbola. The data quality in most of the 1.7 ha area was good and penetration depth reached 3–4 m. In the first step, we used this data to train a RetinaNet for automatic detection of hyperbola. RetinaNet has not been used for hyperbola detection before, but has shown to outperform other CNNs in object detection [
21] and thus is promising for detecting hyperbola in radargrams. In the next step, the velocity and apex location were determined using different methods that are basically edge extraction and subsequent template matching and hyperbola fitting approaches. They are explained in detail below. The quality of detection and velocity determination for each method is be investigated on a smaller part of the area.
2. Materials and Methods
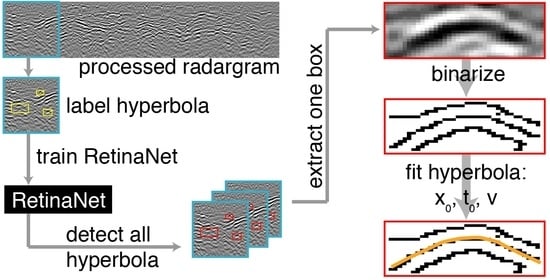
In this section, we first focus on the GPR data acquisition and processing and then provide an overview on RetinaNet, which was used to detect the hyperbola in the radargrams. Afterwards we show the further evaluation of the detected hyperbola, i.e., velocity derivation by different methods and clustering. A general overview of data preparation and the further procedure is also shown in the schematic in
Figure 1 and explained in detail in the following parts.
2.1. GPR Data Acquisition and Processing
The GPR dataset was recorded with a Malå Multichannel Imaging Radar (MIRA) with 16 channels and 400 MHz center frequency. The time range of 100 ns was recorded at 1024 samples and the signal was stacked 4 times. Profile spacing was 8 cm and inline trace distance 3 cm. Accurate positioning was achieved with a Leica total station (TS15).
The data processing was performed with the MATLAB software MultichannelGPR [
39] and consists of (a) DC amplitude removal, (b) time zero correction by shifting of channels 2–15 with relation to channel 1 for each profile by means of cross correlation, (c) adjustment of time zero across all profiles for all channels, (d) bandpass filtering (100–600 MHz), (e) cutting of the time axis at 80 ns, (f) application of a custom gain function with [−20, 0, 10, 20, 30 dB] stretched over the time range of 80 ns, and (g) removal of horizontal reflections with the help of a wavenumber highpass with cutoff wavenumber 0.1 m
−1.
The processed radargrams of all 16 channels were exported as jpeg images using a color scale with the highest 1% of amplitudes as black and the lowest 1% of amplitudes as white and gray scale in between. They were cut into pictures of 256 × 256 pixel size, i.e., 256 traces and the time range of 80 ns was spread onto 256 pixels, while recording the coordinates of each picture in a look-up table for later use. The gray-scale pictures were exported as RGB (red-green-blue) images and thus have three color values for each pixel, as was required for input into the pre-trained RetinaNet.
All 636 images of channel 1 containing hyperbola were used for training and evaluation of the Deep Learning network RetinaNet. The jpeg images of this channel were loaded into MATLAB Image Labeler and bounding boxes were manually assigned to the hyperbola. Then the data was split into 60% training data (381 images), 30% test data (191 images), and 10% validation data (64 images). In these 636 images, 1158 hyperbola were marked manually by bounding boxes as ground truth.
2.2. Hyperbola Detection with RetinaNet
Hyperbola in radargrams can be seen analogous to objects in images. For the detection and classification of objects in images, a wide range of tools exists. All these object detectors have to be trained on labeled images. This means that bounding boxes with a classification (called ground truth) have to be drawn manually in a number of images used for training. During training, a so-called loss function is minimized, which is roughly said to be the summed differences between the ground truth and detected box coordinates (bounding box regression) and the summed differences between the ground truth and detected classes (classification). When training is completed, the current weights of the network layers are fixed and new images can be fed into the network for object detection.
In this study, we used RetinaNet [
21,
22], which is based on Faster R-CNN [
16] combined with a Feature Pyramid Network (FPN). A FPN takes the input image and applies convolutional layers to derive feature maps at different levels. This combination allows the extraction of both low-resolution, semantically strong features and high-resolution, semantically weak features. In addition, to overcome the problem of class imbalance between few objects and a large number of background samples, a new loss function is used, which is called focal loss [
21]. For more details on the network see the references above.
We did not build the network from scratch, but used an existing RetinaNet in a pytorch implementation [
40]. Its architecture is described in
Appendix A. For classification, two classes were used: background and hyperbola, which is not a pre-existing class, but was defined by us. We used ResNet50 (Residual Network with 50 layers) [
41] as the backbone with pretrained weights on the Microsoft COCO dataset [
42] to reduce the training duration. This enables the network to extract features for detecting objects, but not explicitly hyperbola. In order to train the network further to detect the new object class “hyperbola”, we used our training dataset (381 images from channel 1, see above) as input. During this training we used an Adam optimizer with a learning rate of 1 × 10
−5 and reduced the learning rate by multiplication with 0.1 if the loss remained constant over three epochs. One epoch is over if all images used for training are passed through the network. In total, 50 epochs were used. Different batch sizes (1, 2, 4, 8, 16) were tested. This batch size provides the number of images after which the weights of the network layers are adjusted. The calculations were performed on a high-performance computing cluster on 32 Intel Xeon x86-64 cores. The images of the validation dataset were used for performance evaluation during training and the test dataset for the final evaluation after training was completed. The models for different batch sizes were evaluated by calculating the average precision (AP), recall, and precision from the test data. Recall provides the number of actually detected hyperbola (Recall = TP/(TP + FN) with TP: true positive, FN: false negative) and the precision answers the question of how many of the detected hyperbola are actually hyperbola (Precision = TP/(TP + FP) with FP: false positive) [
43]. These two measures were calculated for the first input image and subsequently updated after each following input image and could thus be plotted as a recall–precision curve. The area under the recall–precision curve is called average precision (AP).
After training was completed, all images from all other GPR channels were used as input for the trained RetinaNet and bounding boxes for classified hyperbola were inferred.
2.3. Velocity Derivation from Detected Hyperbola
While the accuracy of the hyperbola detection can be evaluated with the labeled test dataset (AP, recall, precision), we would also like to investigate the accuracy of apex and velocity derivation from the detected hyperbola. Therefore, a smaller test area of 10 m × 15 m was cut from the large dataset. The detected hyperbola in this area were then evaluated with different methods in order to derive the apex location (x0 and t0) and the velocity of the overlying medium. The results of the different methods, which are explained in the following subsections, are evaluated with respect to runtime and accuracy. For the accuracy determination, we derived the “true” apex location and velocity for each of the detected hyperbola manually by means of visually fitting a hyperbola to the radargram. In order to determine the error of apex and velocity determination during manual picking, we carried out this determination three times and calculated the mean and standard deviation. The test velocities were defined from 0.05 up to 0.15 m/ns in steps of 0.005 m/ns. This range was also used as a “valid data range” for the velocities during automatic determination.
The “true” apex locations and velocities, i.e., defined by mean and standard deviation from the three picking passes, were compared to the automatically derived ones by means of RMS errors (Root Mean Square errors). For all the automatic methods, the images in the smaller area were loaded and the detected bounding boxes were extracted. The following procedure applied to the bounding boxes could then be divided into two steps: (1) extraction of potential points on a hyperbola and (2) fitting of these points. For the extraction of potential points on a hyperbola, we used three methods, i.e., a Canny edge filter, minimum and maximum phase, and a threshold combined with subsequent column connection clustering (C3) algorithm. For fitting and deriving the hyperbola parameters, we used template matching (only applied to Canny edge-filtered images), Random Sample Consensus (RANSAC), Hough transform (HT), and least-squares fitting of
x2-
t2-pairs (
Figure 2).
All of these methods have been used individually in the literature before, but we wanted to compare all combinations on a single dataset. This resulted in, overall, 10 different methods for automatic velocity determination inside the bounding boxes: (1) Template matching, (2) Canny edge and RANSAC, (3) Canny edge and HT, (4) Canny edge and x2-t2-fitting, (5) Min/max phase and RANSAC, (6) Min/max phase and HT, (7) Min/max phase and x2-t2-fitting, (8) Threshold and C3 and RANSAC, (9) Threshold and C3 and HT, and (10) Threshold and C3 and x2-t2-fitting. The different parts of these methods are explained in the following sections. To receive valid parameters during hyperbola fitting, we applied following restrictions to the derived parameters or otherwise set them to “invalid”: (a) the velocity has to be between 0.05 and 0.15 m/ns, and (b) the apex location (x0 and t0) has to be inside the bounding box.
2.3.1. Canny Edge Filter
Ref. [
44] proposed a filter to detect edges in noisy images. They first applied a Gaussian filter to suppress noise and then calculated the intensity gradient of the smoothed gray-scale image. Afterwards, the pixels with gradients above a certain threshold were marked as strong edges and between this upper and a second lower threshold as weak edges. All pixels with gradients below the lower threshold were suppressed. In our applied MATLAB function for Canny edge detection, the upper threshold was selected automatically depending on the input data and the lower threshold was determined as 0.4 times the upper threshold. The resulting image was a binary image where 1 represents an edge and 0 the background.
2.3.2. Minimum and Maximum Phase
A very simple hyperbola point extraction method was inspired by ref. [
45], who took the minimum phase points of each trace of a detected hyperbola. Therefore, we took the minimum and maximum amplitude point of each trace, resulting in two sets of points for fitting: one from the minima and one from the maxima. Unfortunately, they do not necessarily need to originate from the detected hyperbola, but could also stem from other high amplitude reflections in the current bounding box. After fitting each set individually, the determined parameters
x0,
t0, and v were averaged. Of course the apex times of minimum and maximum phase were different, but nevertheless, the mean value provides a robust estimate of the temporal location.
2.3.3. Threshold and Column Connection Clustering (C3) Algorithm
This method was proposed by ref. [
33] and includes first the selection of regions of interest by thresholding the radargram and later thinning the regions of interest by finding connected clusters on neighboring traces. We selected half of the maximum amplitude in each detected bounding box as threshold and set all pixels with absolute amplitude above this threshold to one and below to zero. Then the resulting binary image was scanned column-wise from left to right in order to separate different regions into connected clusters. In a column a number of consecutive points higher than s (s = 3 in our case) is called a column segment. If there is a point in the same row on a neighboring column, it is called a connecting element. For each column segment in the first column, it is checked for a connecting element in the second column. If there is a connecting element in the second column with column segment length ≥ s, the cluster will continue. It is also possible that clusters split into two or more clusters. A detailed description of the algorithm can be found in ref. [
33]. For each output cluster of the C3 algorithm, a central string is determined, which is composed of the middle points of the elements in each column for one cluster. Because there are probably more clusters in a bounding box, we chose the one with the longest central string, i.e., the highest number of connected columns and disregarded all other clusters. The points of the longest central string were then used for further fitting.
Because the small images as input for the hyperbola detection are relatively coarse with respect to temporal time step dt = 0.31 ns, using the cut-outs of bounding boxes from these input images resulted in no connecting elements. In order to achieve better correspondence between neighboring traces, i.e., more connecting elements, we upsampled the images inside the bounding boxes to dt/4 by linear interpolation before thresholding and C3 application.
2.3.4. Template Matching
Template matching for hyperbola detection was already applied by ref. [
46] using modeled radargrams as templates. In contrast to using radargrams as input and test image, we used binary representations for both. First, a Canny edge filter was applied to the extracted bounding boxes resulting in binary images and then these binary images were compared with hyperbola templates using a 2D normalized cross correlation. The hyperbola templates were created for different apex times (
t0 between 0 and 79 ns in steps of the sample interval dt) and propagation velocities (
v between 0.05 and 0.15 m/ns in steps of 0.005 m/ns). The resulting cross correlation maps for each velocity were searched for maximum values. To prevent the search to be trapped into local minima at the border, the cross correlation values were weighted with the inverse distance to the zero lag point. Thus, correlations near the center (minimum lags in x and t direction) were amplified. This assumption is valid because the bounding boxes were mostly located with the hyperbola in the middle in x direction and at the top in t direction, which is in accordance with the templates and thus close to zero lag. The location of the global maximum value of the weighted maps then indicates the best velocity and apex location.
2.3.5. Random Sample Consensus (RANSAC)
The RANSAC (Random Sample Consensus) algorithm [
34] can be used to fit a model to noisy data by detecting and ignoring outliers. In our case the model is the equation for a hyperbola:
with
ti: two-way-traveltime at location
xi,
t0: two-way-traveltime at apex location
x0, and
v: propagation velocity. Our noisy data consists of m x-t-pairs derived from the methods explained in
Section 2.3.1,
Section 2.3.2,
Section 2.3.3 and for a well-determined set of equations we need at least three of these m points for fitting and deriving the three unknown parameters
x0,
t0, and
v. For the RANSAC algorithm, we defined a number of sample points
n (in our case
n = 3) that were randomly taken from the m input points. Subsequently the model was fitted to these randomly chosen sample points and the number of points from the complete dataset within a certain error tolerance e (in our case
e = 5 pixels in time direction) is determined. We call these points inliers as opposed to outliers. This was performed 50 times (in our case) and the sampling subset with the maximum number of inliers used to fit the model and derive the unknown parameters finally. For this final fitting, not only the
n subset points were used, but rather the
n points plus
i inliers.
2.3.6. Hough Transform (HT)
The Hough transform (HT) was originally intended for finding straight lines in an image [
47], but was further extended for the detection of general geometrical shapes in binary images [
48]. A hyperbola can also be such a geometrical shape, which is described by the three parameters
x0,
t0, and
v. All points derived by the methods explained in
Section 2.3.1,
Section 2.3.2,
Section 2.3.3 were transformed into the parameter or Hough space according to the equation for a hyperbola (Equation (1)). The Hough space was determined by the valid ranges of the three unknown parameters:
v between 0.05 and 0.15 m/ns,
t0 in the time range of the bounding box and
x0 around the vertical symmetry axis ±
w/4, where
w is the width of the bounding box. The location of the vertical symmetry axis was determined by calculating the symmetry of the binary image inside the bounding box as provided by ref. [
29] and references therein. As maximum calculation column width, we used
w again. This reduction of the valid parameter range of
x0 decreased the calculation time of the HT.
For all points taken from the binary image, the temporal apex location t0 was calculated for all x0 and v combinations using Equation (1). If the calculated t0 was within the valid range, the Hough space at this location (x0, t0, v) increased by one. The point with the maximum number of counts was taken as the best match.
2.3.7. Least-Squares Fitting of x2 − t2-Pairs
By rearranging Equation (1) one can yield
which corresponds to a linear equation of type
y′ = a + mx′ with
,
,
and
. Thus, the velocity
v can be directly derived from the slope and
t0 from the intercept of a straight line fitting pairs of
x′ and
y′. The apex location
x0 is determined by fitting a straight line to
x′-
t′-pairs with all different
x′ taken as
x0. The fit with the smallest RMS error indicates the right
x0 value.
2.4. Clustering of Hyperbola
In rebar or pipe detection, it is relatively straightforward to connect detected apex points of hyperbola arranged in a straight line to one object, e.g., a pipe. In an archaeological context, where hyperbolae originate mainly from point-like objects such as stones, these will produce hyperbola on adjacent profiles all originating from a single point. Therefore, one has to find these hyperbolae belonging together and determine the true location of the object.
In order to group hyperbolae originating from the same subsurface object, we applied Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [
49]. The input data for the algorithm are the 3D locations of the determined apex points provided by Easting, Northing, and
z. The depth
z is determined by
z =
t0/2 ×
v. The velocity
v for this calculation is not taken from the automatic determination directly, but from a linear fit of the mean velocities determined in time intervals of 10 ns starting from 0 ns reaching to 80 ns. If the automatically determined velocities would have been taken, errors in them would result in very different depths of the hyperbola belonging to one cluster and thus they would not be clustered. When a mean velocity is taken instead, outliers are neglected and clustering is more robust.
For clustering, first, one point of this input data was chosen as current point and all points within a certain radius r (0.25 m in our case) were defined as neighbors. If the number of neighbors is above a value minpts (2 in our case), the current point was defined as a core point belonging to cluster c. All neighboring points were then taken iteratively as the current point and if they had more neighbors than minpts inside r they were also labeled as core points belonging to cluster c. If the number of neighbors was below minpts, the current point was labeled as an outlier. Afterwards the next-until-now unlabeled point was chosen as the current point and the cluster number c was increased. The outputs of the algorithm were the cluster numbers for each input point or −1 if they were outliers and were not assigned to a cluster. All hyperbolae belonging to one cluster were merged into one, where the horizontal coordinates are represented by the mean of the coordinates of all hyperbolae, the temporal coordinate by the minimum t0, and the velocity of the overlying medium by the mean of all velocities.
2.5. Evaluation of the Velocity Determination Algorithm
For evaluation of the correctness of determined velocities, we have to consider different errors originating from following sources:
(Partial) masking and/or distortion of hyperbolae through other reflection events;
Errors in positioning and thus distortion of hyperbolae;
Erroneous assumptions about the antenna offset and object radius;
Inaccurate picking of hyperbolae from radargrams.
The error from the first source cannot be quantified uniquely, being different for each individual subsurface structure. The second could in principle be determined, but is different for each channel, profile, and along the profile. Thus, we neglected it here. Nevertheless, we can try to estimate the errors from the last two sources with a modeling study. Hyperbolae were, in general, calculated using Equation (1). The depth of the object (
D) is directly related to travel time
t0 with
. Equation (1) is only valid for zero offset antennae (no distance between transmitter and receiver) and for point objects (
Figure 3a). In reality, there is normally an offset between transmitter and receiver (2
B) and objects have a finite size, approximated as spheroids with radius
r (
Figure 3b). The equation taking these quantities into account is as follows [
50]:
See the definition of variables in
Figure 1. In real-world applications, the antenna offset is known or can at least be estimated, but the radius of the object is unknown. If we now use the simple formula Equation (1) to derive the velocity and depth of the object from a measured radargram, we introduce errors, because the hyperbola in the radargram obeys Equation (3).
2.5.1. Velocity Dependence on Offset and Object Size
To quantify the errors introduced by this procedure, we performed two modeling studies: (a) we calculated “exact” hyperbola based on Equation (3) and estimated the velocity and depth with the simple Equation (1) and thus neglected offset and radius, and (b) we calculated “exact” hyperbolae based on Equation (3) and only took the right radius of the object into account, but still zero offset. The resulting depth and velocity were compared with the real ones and thus an error could be calculated. In the calculations we used a half offset B = 0.075 m.
2.5.2. Velocity Dependence on Picked Phase
When picking hyperbolae manually, one needs to decide which phase to pick. From our experience, the choice will always be different and depends on which one is best visible. However, what error is introduced through picking the minimum phase on one hyperbola and the maximum phase on the next? This also not only accounts for manual picking, but also for the automatic fitting. In order to estimate the errors of picking different phases, a radargram was modeled above an object with radius 0.1 m in a depth of 0.5 m and with two different relative permittivities of the surrounding material (10 and 25). Thus, the theoretical velocities were 0.095 m/ns and 0.06 m/ns, respectively. For modeling we used the open-source software gprMax [
51] with a ricker wavelet of 400 MHz and a trace spacing of 2 cm. The offset between transmitter and receiver was 15 cm. The resulting radargrams were cut out around the hyperbola and minimum and maximum phases were picked automatically. The velocity and depth of the object were determined with simple Equation (1) and exact Equation (3).