Investigation on Vertical Position and Sound Velocity Variation for GNSS/Acoustic Seafloor Geodetic Calibration Based on Moving Survey Data

Abstract

The accuracy of GNSS/Acoustic seafloor geodetic calibration is greatly influenced by the temporal variation of sound velocity, especially in the vertical direction. Aiming at correcting of the unknown parameters related to both the positions and the sound velocity, this paper proposes a step-by-step inversion scheme based on moving survey data. The proposed method firstly estimates the horizontal normalized travel time delay with sound ray tracing strategy and then computes the horizontal position with circle line observations. We reconstructed an inversion scheme for extracting the surface sound velocity disturbance (SSVD) and corrected the vertical position from cross line data. The SSVD is decomposed into a sum of different period disturbances, and a new SSVD is reconstructed by combining the long period disturbance and short period disturbance. The proposed algorithm is verified by the South China Sea experiment for GNSS/Acoustic seafloor geodetic calibration. The results demonstrate that the new method can take the effects of sound velocity variation into consideration and improve the precision of the vertical position, which is superior to the least squares (LS), the single-difference LS for seafloor geodetic calibration.

1. Introduction

The GNSS/Acoustic (GNSS/A) technique was devised in the 1980s [1], which is a combination technique of kinematic GNSS positioning and underwater acoustic ranging for seafloor geodetic absolute positioning. Since the seafloor geodetic benchmarks for detecting absolute seafloor crustal deformations were established, it has yielded many significant results, including detection of interseismic [2,3], coseismic [4,5], and postseismic deformation associated with earthquake [6,7], as well as plate motions [8,9,10,11]. However, the positioning service or deformation analysis using the seafloor benchmarks is affected by the accuracy of locations of seafloor benchmarks. Thus, it is necessary to improve the accuracy of the seafloor geodetic absolute calibration and realize efficient observations.

The observation accuracy of GNSS/A is mainly limited by the acoustic ranging error, especially caused by the temporal fluctuations of sound velocity within the observation period [12,13,14]. In general, the sound velocity is generally assumed to be vertically stratified in seawater with the underwater acoustic signals conforming to Snell’s law. By adopting the sound ray-tracing (SRT) strategy based on the sound velocity profiles (SVPs) data, the propagation paths of acoustic signals can be tracked [15,16]. The sound velocity is not only affected by seasonal and daily variations in ocean conditions but also by more detailed temporal and spatial variations caused by several factors such as internal waves, anomalous temperature and water masses [17]. There are difficulties for the SVP data to balance real-time and accurate demands due to the time fluctuation of sound velocity within tens of minutes to a few hours, especially during moving calibration surveys. As for GNSS/A absolute calibration observation, the single transponder is positioned by controlling the vessel sailing around a circle with a nominally constant radius [18,19]. The surveying strategy is effective in precisely determining the horizontal components of the center transponder, since systematic errors have been cancelled out [2,20]. However, the accuracy of vertical components remains difficult to improve, limited by the sound velocity temporal variation, especially surface sound velocity disturbance [21].

Many previous GNSS/A studies have proposed several methods to correct the effect of sound velocity variation. Osada et al. succeeded in estimating the temporal variation of sound velocity from acoustic data [22]. Xu et al. proposed a single difference (SD) method for single point seafloor positioning and the double difference method for relative seafloor positioning to remove the effect of systematic errors [13]. The simulations have shown that the accuracy of single point positioning can be determined with one centimeter in the three dimensions, and the performance remains to be further validated using the field data. When the reference sound velocity profile is different from the actual profile, it ultimately affects the discrepancy between the estimation of the propagation time delay. Fujita et al. removed this effect by using a simple time function to estimate the temporal variation of the acoustic velocity structure [14]. The results showed that the temporal and spatial stability of the acoustic velocity structure in the seawater depend on the region and season. Kido et al. proposed a generalized expression of sound velocity variation in terms of a travel time residual normalized to the vertical component to acoustically estimated sound velocity [23]. This method also provides a reference for many future studies [2,5,7,24,25]. Chen et al. estimated the relative positions of three transponders and a constant sound velocity bias by an optimization technique combined with ray-tracing calculations [26]. The results show that the accuracy of relative positioning is insensitive to the surface sound velocity disturbance at a depth of 300 m. In the last ten years, analytical procedures with the estimation of the spatial sound velocity gradient for the moving-around pattern have been developed. Yokota et al. proposed a technique for extracting the gradient effects of sound velocity structure through multiple modeling [3]. Honsho et al. showed a more general expression for one-directional sound velocity gradient, and the accuracy of the seafloor positioning was also improved by the above inversion scheme [7]. However, most of those studies have basically adopted the Scripps Institution of Oceanography (SIO) approach [1], which locates a virtual geodetic station and estimates the sound velocity variation using the transponders array. In GNSS/Acoustic seafloor geodetic absolute calibration, each seafloor transponder is an independent geodetic station [27], and the influence of sound velocity variation on ranging error is intuitively related to various factors such as propagation time, incidence angle and depth, which increase the complexity of data processing.

There are two key points involved in vertical positioning and sound velocity variation. One is the observation configuration optimization that can be constructed by designing different survey lines and the array of seafloor stations, and the other is to determine the appropriate inversion scheme for solving the optimization problem. As for the data post-processing, the observation configuration has been determined. Thus, we focus on the improvement of the inversion scheme. In this contribution, the step-by-step inversion scheme has been proposed to simplify the difficulty of parameter estimation and to improve the positioning accuracy in the vertical direction based on the moving survey data. Furthermore, in the experiment, the cross-survey lines over the top of the transponder are arranged. In order to improve the vertical accuracy and estimation efficiency of the absolute positions of the seafloor reference stations, we performed a vertical position inversion and sound velocity perturbation inversions iteratively to obtain the final solutions from cross line data. Finally, we discuss our results on the South China Sea experiment.

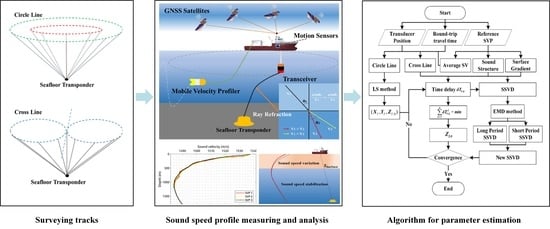
2. Principles of the GNSS/Acoustic Seafloor Geodetic Move-Around Calibration Method

2.1. Observation System

A conceptual model of the seafloor absolute calibration system is shown in Figure 1, which refers to the process of transferring positioning from a surface positioning system referenced to a global reference frame to a seafloor transponder. This typically involves the simultaneous observation of the GNSS positioning and the attitudes of a vessel while acoustically ranging toward the fixed seafloor transponder from a transducer and known offsets from the GNSS antenna on the vessel. A single transponder is positioned by controlling the vessel sailing around a circle with a nominally constant radius to remove systematic errors. By collecting geometrically symmetric data, the positioning accuracy and observation efficiency tend to be improved [28,29,30,31]. In order to ensure geometric structure of the observation, the radius of the circle that the surveying vessel sails around is approximately 50% to 150% of the water depth. The distance between the seafloor transponder and the vessel transducer is estimated by acoustic round-trip traveling time.

The sound velocity can be measured by a velocimetry or computed from measurements of the water temperature, salinity and pressure using a conductivity temperature depth (CTD) profiler [32]. However, the temperature varies significantly with time and space, particularly in shallow parts, and the accuracy of the sound velocity is limited by the empirical equations that relate these parameters to sound velocity.

2.2. Basic Ray-Tracing Strategy for GNSS/Acoustic Absolute Calibration

The basic principles of the GNSS/Acoustic absolute calibration during an interrogation/reply cycle are shown in Figure 2a. When the vessels steam around a circle, the location of the vessels is changed, and the round-trip traveling time for interrogation and reply must be calculated separately.

Assuming a laterally stratified sound velocity structure, to estimate the transponder position ${\mathit{P}}_T=[\begin{array}{ccc}{\mathit{X}}_T& {\mathit{Y}}_T& {\mathit{Z}}_T\end{array}]$ precisely, let ${\mathit{P}}_{S,k}=[\begin{array}{ccc}{\mathit{X}}_{S,k}& {\mathit{Y}}_{S,k}& {\mathit{Z}}_{S,k}\end{array}]$ be the positions of the transceiver at the time of sending and ${\mathit{P}}_{R,k}=[\begin{array}{ccc}{\mathit{X}}_{R,k}& {\mathit{Y}}_{R,k}& {\mathit{Z}}_{R,k}\end{array}]$ be the positions of the transceiver at the time of receiving acoustic signals. The observation equation expressing the round-trip travel time for the seafloor transponder at time k is represented as:

$$T_{m,k}=T_{S,k}+T_{R,k}+{\epsilon }_k$$

(1)

with

$$T_{S,k}=f({\mathit{P}}_T,{\mathit{P}}_{S,k},{\mathit{C}}_k),T_{R,k}=f({\mathit{P}}_T,{\mathit{P}}_{R,k},{\mathit{C}}_k)$$

(2)

where $T_{m,k}$ represents the measured round-trip acoustic travel time. As shown in Figure 2a, the one-way travel time $T_{S,k}$, $T_{R,k}$ can be calculated using the ray-tracing technique with sound velocity profile $\mathit{C}$ based on Snell’s law. ${\epsilon }_k$ represents the random timing error.

The error equation of round-trip travel time can be expressed as:

$${\mathit{V}}_k=T_{m,k}-f({\mathit{P}}_{T,o},{\mathit{P}}_{S,k},{\mathit{C}}_0)-f({\mathit{P}}_{T,o},{\mathit{P}}_{R,k},{\mathit{C}}_0)-\Delta T_{P,k}-\Delta T_{C,k},$$

(3)

$$\Delta T_{P,k}\approx f({\mathit{P}}_T,{\mathit{P}}_{S,k},{\mathit{C}}_k)+f({\mathit{P}}_T,{\mathit{P}}_{R,k},{\mathit{C}}_k)-f({\mathit{P}}_{T,o}+\delta {\mathit{P}}_T,{\mathit{P}}_{S,k},{\mathit{C}}_k)-f({\mathit{P}}_{T,o}+\delta {\mathit{P}}_T,{\mathit{P}}_{R,k},{\mathit{C}}_k),$$

(4)

$$\Delta T_{C,k}\approx f({\mathit{P}}_T,{\mathit{P}}_{S,k},{\mathit{C}}_k)+f({\mathit{P}}_T,{\mathit{P}}_{R,k},{\mathit{C}}_k)-f({\mathit{P}}_T,{\mathit{P}}_{S,k},{\mathit{C}}_0+\delta {\mathit{C}}_k)-f({\mathit{P}}_T,{\mathit{P}}_{R,k},{\mathit{C}}_0+\delta {\mathit{C}}_k),$$

(5)

where ${\mathit{P}}_{T,o}$ represents the initial transponder position, ${\mathit{C}}_0$ represents the reference sound velocity profile, $\Delta T_{P,k}$ and $\Delta T_{C,k}$ denote the ray-tracing time error by position basis $\delta {\mathit{P}}_T$ and sound velocity temporal variation $\delta \mathit{C}$, respectively.

The error sum of squared errors between the measured and calculated travel times is written as follows:

$$\mathit{J}(\delta {\mathit{P}}_T,\delta {\mathit{C}}_k)={\displaystyle \sum _{k=1}^n{\mathit{V}}_k^2},$$

(6)

where n is the number of acoustic observation pairs. When the average sound velocity along the actual ray path is expressed as $C_m$, the Euclidean distances and the transceiver and the transponder position can be calculated with the least square (LS) method; see Appendix A.

Kido et al. represented the temporal variation of sound velocity as a vertically normalized time delay relative to that for a reference model [23], which is called the Nadir Total Delay (NTD) [24]. Using the mapping function, the horizontal and vertically normalized travel time delay can be represented as follows:

$$\delta T_{H,k}=T_{m,k}\frac{2\sin ({\theta }_{S,k}^{})\sin ({\theta }_{R,k}^{})}{\sin ({\theta }_{S,k}^{})+\sin ({\theta }_{R,k}^{})}-T_{S,k}\sin ({\theta }_{S,k}^{})-T_{R,k}\sin ({\theta }_{R,k}^{}),$$

(7)

$$\delta T_{V,k}=T_{m,k}\frac{2\cos ({\theta }_{S,k}^{})\cos ({\theta }_{R,k}^{})}{\cos ({\theta }_{S,k}^{})+\cos ({\theta }_{R,k}^{})}-T_{S,k}\cos ({\theta }_{S,k}^{})-T_{R,k}\cos ({\theta }_{R,k}^{}),$$

(8)

where the travel-time delay $\delta T_{H,k}$ and $\delta T_{V,k}$ normalized by the mapping function are independent of the vertical and horizontal distance of the transducer, respectively.

Note that, if the sound velocity perturbation $\delta c$ is a constant bias, based on the geometric symmetry of a circular track, the horizontal travel-time residual $\delta T_{H,k}$ has a smaller effect on horizontal positioning. Meanwhile, the vertically travel-time residual normalized by the mapping function is independent of the horizontal distance of the transducer [33]. As shown in Figure 2b, if the depth error $\delta d$ exists, the vertically travel-time residual normalized by the mapping function varies depending on the horizontal distance from the transducer to the transponder. The vertically normalized travel time delay can be represented as follows:

$$\delta {\mathit{T}}_{V,i}\approx \frac{d_i}{\sqrt{h_i^2+d_i^2}}\left(\frac{\sqrt{h_i^2+{(d_i^{}+\delta d)}^2}}{C+\delta c}-\frac{\sqrt{h_i^2+d_i^2}}{C}\right),$$

(9)

According to the Equation (9), the vertically normalized travel time delay includes not only information on the range, but also that on the velocity structure along the path. This also indicates that the sound velocity error and the depth error cannot be distinguished from the same incident angles for the transponders. Other observations with different indicant angles are essential to precisely estimate vertical displacements. During the acoustic absolute calibration, the sound velocity variation function $\delta c$ is usually given as a simple time function.

3. Inversion Scheme

3.1. Absolute Horizontal Position Estimation

In this research, the horizontal and vertical position are estimated to utilize a step-by-step method for moving survey data. We design two kinds of calibration survey lines, as shown in Figure 3: one is the circular line (Figure 3a), the other is the cross line (Figure 3b).

In this research, these two types of survey lines are used to calculate the horizontal (2D) and vertical coordinates of the seabed reference station, respectively. As the LS method with circular calibration trajectory is insensitive to the sound velocity perturbation, it is possible to calculate the precision horizontal position precisely. The horizontal position can be used as the constraint to estimate the vertical position and the surface sound velocity disturbance (SSVD). The unknown horizontal position can be estimated by solving the nonlinear Equation (7) for all circle line travel time data using the iterative least squares method. The nonlinear equation is locally linearized as follows:

$$\begin{array}{l}\delta {\mathit{T}}_{H,k}^{Circle}=[\frac{\sin {\theta }_{S,k}^{}\delta {\mathit{f}}_S}{\delta {\mathit{X}}_T}|{\mathit{X}}_{T,o}+\frac{\sin {\theta }_{R,k}^{}\delta {\mathit{f}}_R}{\delta {\mathit{X}}_T}|{\mathit{X}}_{T,o}\frac{\sin {\theta }_{S,k}^{}\delta {\mathit{f}}_S}{\delta {\mathit{Y}}_T}|{\mathit{Y}}_{T,o}+\frac{\sin {\theta }_{R,k}^{}\delta {\mathit{f}}_R}{\delta {\mathit{X}}_T}|{\mathit{X}}_{T,o}]\left[\begin{array}{c}\delta {\mathit{X}}_T\\ \delta {\mathit{Y}}_T\end{array}\right]\\ =\left[\frac{{\kappa }_{S,k}\sin {\theta }_{S,k}^{}({\mathit{X}}_{T,o}-{\mathit{X}}_{S,k})}{H_{S,k}}+\frac{{\kappa }_{R,k}\sin {\theta }_{R,k}^{}({\mathit{X}}_{T,o}-{\mathit{X}}_{R,k})}{H_{R,k}}\frac{{\kappa }_{S,k}\sin {\theta }_{S,k}^{}({\mathit{Y}}_{T,o}-{\mathit{Y}}_{S,k})}{H_{S,k}}+\frac{{\kappa }_{R,k}\sin {\theta }_{R,k}^{}({\mathit{Y}}_{T,o}-{\mathit{Y}}_{R,k})}{H_{R,k}}\right]\left[\begin{array}{c}\delta {\mathit{X}}_T\\ \delta {\mathit{Y}}_T\end{array}\right]\end{array}$$

(10)

where ${\kappa }_{S,k}$ and ${\kappa }_{R,k}$ are sending and receiving Snell’s constant and are computed by the ray-tracing. $H_{S,k}=\sqrt{{({\mathit{X}}_{T,o}-{\mathit{X}}_{S,k})}^2+{({\mathit{Y}}_{T,o}-{\mathit{Y}}_{S,k})}^2}$, and $H_{R,k}=\sqrt{{({\mathit{X}}_{T,o}-{\mathit{X}}_{R,k})}^2+{({\mathit{Y}}_{T,o}-{\mathit{Y}}_{R,k})}^2}$.

The observations of different incident angles through different cross lines are sensitive to vertical deviation and sound velocity disturbance. Thus, this observation pair also provides basis information for the inversion of coupled surface sound velocity disturbances and vertical deviations. To estimate the vertical position, it is necessary to find the best $\delta {\mathit{Z}}_T$ and $\delta {\mathit{C}}_k$ to minimize the following objective function:

$$\mathit{J}(\delta {\mathit{Z}}_T,\delta {\mathit{C}}_k)={\displaystyle \sum _{k=1}^n\delta {\mathit{T}}_{V,k}^2}$$

(11)

3.2. Surface Sound Velocity Temporal Variation Extraction Method

The absolute position of a transponder and temporal sound velocity variation can be estimated by finding the best values to minimize Equation (6). A variety of effective optimization algorithms, e.g., Bayesian least squares inversion [14], numerical optimization approach [26], linearized inversion method [3], extended Kalman filter [33], one step approach [7], are developed with different kinds of temporal sound velocity variation. In order to improve the vertical accuracy and estimation efficiency of the absolute calibration position, we performed a vertical position and sound velocity perturbation inversions iteratively to obtain the final solutions. The sound velocity perturbation inversion method was developed by Fujita et al. [14]. The shape of the vertical profile is also assumed to be invariable with time. Different from Fujita’s method, for the absolute correction of a single transponder, this study only calculates the surface sound velocity disturbance (SSVD).

As shown in Figure 4, the reference sound velocity profile is divided into two parts: the shallow water area and the deep water area. Our method takes into account the shallow water sound velocity disturbances affected by the outside environment and reduces the number of inversion parameters. Consider that the surface sound velocity disturbance $\delta {\mathit{C}}_k(z)$ varies in time with depths shallower than $Z_{Surface}$, then $\delta {\mathit{C}}_k(z)$ can be rewritten as the sum of intrinsic model functions (IMFs) $u$ and residual $r$:

$$\delta {\mathit{C}}_k(z)=\{\begin{array}{cc}{\mathit{r}}_m(k)+\sum _i^{\mathrm{m}}{\mathit{u}}_i(k)& (z\le Z_{Surface})\\ 0& (z>Z_{Surface})\end{array},$$

(12)

Another important step is to calculate the $\delta {\mathit{C}}_k(z)$ based on vertically normalized travel time delay $\delta {\mathit{T}}_V$ and SRT method. In this study, the $\delta {\mathit{C}}_k$ is calculated using the following SSVD extraction method (Algorithm 1).

Algorithm 1 Surface sound velocity variation extraction method

1 . Input: ${\mathit{P}}_{T,o}$, ${\mathit{P}}_S$, ${\mathit{P}}_R$, ${\mathit{T}}_m$, ${\mathit{C}}_0(z)$ 2 . Recursive computation: For k = 1, 2, 3, … $\mathit{C}(z)=C_0(z)$;   While True   (1) Compute the gradient of $\mathit{C}(z)$;   (2) Estimate the incident angle ${\theta }_{S,k}^{}$ and ${\theta }_{R,k}^{}$;   (3) Estimate the travel time $T_{S,k}$ and $T_{R,k}$;   (4) Estimate the vertically normalized travel time delay $\delta T_{V,k}$ using Equation (8);   (5) Estimate the SSVD $\delta {\mathit{C}}_k$     If $\delta T_{V,k}<\gamma$      Break;     Else if $\delta T_{V,k}>0$      $\mathit{C}(z)=\{\begin{array}{c}\mathit{C}(z)+\kappa \\ \mathit{C}(z)\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}(z\le Z_{Surfacce})\\ (z>Z_{Surfacce})\end{array}$; ($\kappa$ is a small search step)     Else      $\mathit{C}(z)=\{\begin{array}{c}\mathit{C}(z)-\kappa \\ \mathit{C}(z)\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}(z\le Z_{Surfacce})\\ (z>Z_{Surfacce})\end{array}$;     End $\delta {\mathit{C}}_k=\mathit{C}(z)-{\mathit{C}}_0(z)$; End for Output: $\delta \mathit{C}$.

Recursions (1)–(3) compute the round-trip travel time based on the classical SRT method. Recursions (4) estimate the vertically normalized travel time delay $\delta T_{V,k}$ using Equation (8) and the round-trip travel time ${\mathit{T}}_m$. Recursions (5) compute the SSVD $\delta {\mathit{C}}_k$ using a small search step to let the $\delta T_{V,k}$ be close to zero.

3.3. Absolute Vertical Position and SSVD Estimation

This study utilizes the numerical optimization iterations approach to estimate the vertical position of a seafloor transponder and SSVD. For previous research, the SSVD are usually reconstructed by a combination of series of the basis function:

$$\delta {\mathit{C}}_k=\mathit{\alpha }+{\displaystyle \sum _i^{}{\mathit{\beta }}_i{\mathit{\Gamma }}_i(k)}+{\mathit{\eta }}_{i}r(k)\cos (\gamma (k)-{\gamma }_a),$$

(13)

where $\mathit{\alpha }$ is a constant of sound velocity, and ${\mathit{\beta }}_i$ and ${\mathit{\eta }}_i$ are the coefficients of the basis function. ${\mathit{\Gamma }}_i(t)$ represents the basis function with different periods, e.g., second degree polynomial, or quadratic curve, $r(t)$ is the horizontal distance from transponder to transducer, $r(k)\cos (\gamma (k))$ indicates the vessel position at time t, and ${\gamma }_a$ represents the horizontal gradient effect.

Considering the complex of the SSVD during the moving survey, in this research, the $\delta \mathit{C}$ is analyzed by the Empirical Mode Decomposition (EMD) method, as shown in Appendix B, which is a time–frequency analysis method to process non-linear and non-stationary signals [34]. EMD can decompose the $\delta \mathit{C}$ to a sum of some IMFs ${\mathit{u}}_i$ with different periods and residual ${\mathit{r}}_m$ adaptively without any prior knowledge.

$$\delta \mathit{C}={\displaystyle \sum _{i=1}^m{\mathit{u}}_i+{\mathit{r}}_m},$$

(14)

As shown in Figure 5, for estimating the vertical position and SSVD, two kinds of calibration survey line observations are used to estimate the horizontal position and vertical position, respectively. The horizontal position calculated by the circle line is used directly to estimate other unknown parameters. We utilize a certain acoustic velocity structure to estimate the vertical position with the cost function $\mathit{J}(\delta {\mathit{Z}}_T,\delta {\mathit{C}}_{Surface})$. Then, we recompute the vertically normalized travel time delay. The SSVD is extracted using the above SRT method. We iterate this process until the position parameters converge.

The EMD method can be utilized to distinguish the effect between the sound velocity variation and the depth error. The surface sound velocity perturbation might have short time periods and long time periods, whereas some previous studies have already proved it [17]. In particular, to distinguish the effect of the vertical basis and the long period disturbance, the relevance index should be computed and adjusted. In our method, the SSVD is decomposed into a sum of different period disturbances, and a new SSVD is reconstructed by combining the long period disturbance and short period disturbance.

4. Experimental Analysis

To analyze the GNSS/Acoustic seafloor geodetic absolute calibration precision, we utilized data from a moving survey calibration experiment in the South China Sea (19°42′ N, 115°08′ E) with a depth of 1750 m on 3 April 2021, as shown in Figure 6. The raw data mainly included the GNSS observations, ship attitudes, round trip travel times of acoustic signals, GNSS offset from the GNSS antenna to the transceiver and sound velocity profiles. The kinematic GNSS observations were obtained using the Veripos APEX with an approximately horizontal and vertical accuracy 10 and 20 cm, respectively. The attitude of the survey ship was obtained using the POS MV 320 of Applanix company (Richmond Hill, ON, Canada). The acoustic ranging data was obtained using the HiPap 102PMGC of Konsberg company (Konsberg, Norway) high precision acoustic positioning system with ultra-long range capabilities (cymbal model) and a cNODE transponder, measuring the travel times of acoustic signals with an approximate range accuracy of 0.02 m. During the trial period, a single transponder was set on the seafloor lander as the entity geodetic station.

After the lander was deployed on the seafloor, the vessel sailed according to the predetermined circle track lines (Figure 7a) and cross track line (Figure 7b) centered on the seafloor station. The number of all acoustic observations was about 5150, and the sampling rate was 4 s.

Table 1. The information of acoustic measurements.

Trajectory	Time First Sample	Time Last Sample	Number of Samples
A circle, R = 2000	3 April 2021 04:11	3 April 2021 06:25	2006
A circle, R = 1000	3 April 2021 06:43	3 April 2021 08:19	1148
A eight, R = 1000	3 April 2021 08:31	3 April 2021 10:27	2004

shows the data list of acoustic measurements at the seafloor reference points.

As shown in Figure 8a, the average incident angles of the big circle and small circle are 43° and 28°. The incident angles of the cross line (eight track) are distributed from 0° to 45°. Three sound velocity profilers in seawater were measured by MVP 300 from the AML Oceanographic company, and the resulting profiles are shown in Figure 8b. The time span of these extracted data was approximately 6 h, ranging from 3:40:00 to 8:20:00 in Coordinated Universal Time (UTC). The average profile of three SVPs is utilized as the reference SVP in this study, and the mean velocity is about 1492 m/s.

To estimate the absolute horizontal position of a seafloor transponder, we used the circle line observation. As shown in Figure 9a, the round trip travel times of big circle and small circle track are approximately 3.4 and 2.7 s, respectively. Using the ray-tracing calculations and Equation (7), the travel time delay and horizontal normalized travel time delay can be estimated, as shown in Figure 9b. The root mean square (RMS) values of the travel time delay and horizontal normalized travel time delay are 0.18 and 0.11 ms, respectively.

The travel time delay and horizontal normalized travel time delay are utilized to estimate the horizontal position with LS method, respectively. Figure 10 shows the histogram of acoustic horizontal range residuals for two LS methods. The RMS of the range residuals for travel time delay and horizontal normalized travel time delay are 13.21 and 8.26 cm, respectively. In addition, the range residuals had mean values of 3.48 and 2.12 cm, respectively. Even though the horizontal range precision in horizontal positioning is limited by systematic errors, the mean value of slant range residuals for the circle line is close to zero. Furthermore, the horizontal position can be utilized to estimate the vertical position and surface sound velocity disturbance.

To estimate the absolute vertical position of a seafloor transponder, we used the cross line observation. As shown in Figure 11a, the round trip travel times vary from 2.3 to 3.3 s. Using the ray-tracing calculations and Equation (8), the travel time delay and vertical normalized travel time delay can be estimated, as shown in Figure 11b. The root mean square (RMS) values of the travel time delay and vertical normalized travel time delay are 0.22 and 0.21 ms, respectively. The mean value of travel time delay and vertical normalized travel time delay are −0.83 and −0.68 ms, respectively. The effect of the delay on the ranging results in an uncertainty of about half a meter in vertical positioning. The IMFs of different periods can be calculated according to the SSVD extraction method in Section 3.2 by setting different surface depths as the initial condition. As shown in Figure 12a, the larger the reference depth is set, the smaller the SSVD value will be. The SSVD can be decomposed with different IMFs, as shown in Figure 12b. Although the amplitude of IMFs is different, the tendency of the IMFs with different reference depths is similar. Considering that the temporal and spatial variation of the surface sound velocity of seawater is more obvious and the variation range is larger, the reference water depth is selected as 300 m in this paper.

The vertical position and SSVD can be estimated by the new numerical iterations approach mentioned in Section 3.3. The new SSVD is constructed using IMFs of different cycles and is then used to iteratively calculate the vertical component. As shown in Figure 13a,b, the vertical range residual with different iterations reduced step by step, and the periodic fluctuations associated with SSVD were gradually eliminated.

The LS method, least squares with unknown sound velocity (LS + C) method in which the average bias of sound velocity is regarded as unknown parameters, the SD least squares method, and the new numerical iterations approach were conducted and compared for underwater acoustic positioning.

Table 2. The residuals statistics of all methods for vertical position.

Method	RMS (cm)	Max (cm)	$\mathbf{Mean} \left(\left|{\mathit{V}}_{\mathbf{V}}\right|\right)\left(\mathbf{cm}\right)$
LS	32.6	104.1	25.9
LS + C	26.5	82.2	18.6.
SD	18.6	72.8	14.7
New method	7.3	26.7	5.7

presents the residuals statistics of different algorithms for vertical position. For the case of underwater 1750 m depth, the vertical RMS of SD and new method are 18.6 and 7.3 cm compared to the 32.6 cm of LS, with an improvement of 42.9% and 77.6%. The vertical Max and Mean of the new method is significantly better than the other three schemes.

5. Conclusions

This study presents an approach of correction for vertical position and sound velocity variation on GNSS/Acoustic seafloor geodetic calibration with moving survey data. The horizontal and vertical positions are estimated to utilize a step-by-step method with circle and cross line survey data. After the validation from a real example, the following conclusions can be drawn.

For the horizontal position component, the symmetric circle line reduced the influence of sound velocity errors and ensured the correctness of the horizontal estimation. The horizontal position can be utilized to estimate the vertical position and surface sound velocity disturbance.

To overcome the vertical defects of the GNSS/acoustic technique, the new numerical iterations were studied. We utilize a certain acoustic velocity structure to estimate the vertical position and SSVD with the vertical normalized travel time delay of the cross line. The SSVD is decomposed into a sum of different period disturbances, and a new SSVD is reconstructed by combining the long period disturbance and short period disturbance. The estimation results illustrated that the GNSS/acoustic calibration precision can be improved by implementing the numerical iterations method.