Weighted Mean Temperature Hybrid Models in China Based on Artificial Neural Network Methods
Abstract
:1. Introduction
2. Study Area and Methods for Calculating Tm
2.1. Study Area
2.2. Method of Calculating Tm
2.2.1. Calculation of Tm Based on Radiosonde Data
2.2.2. Calculating Tm Based on the UNB3m Model
2.2.3. Calculating Tm Based on the GPT3 Model
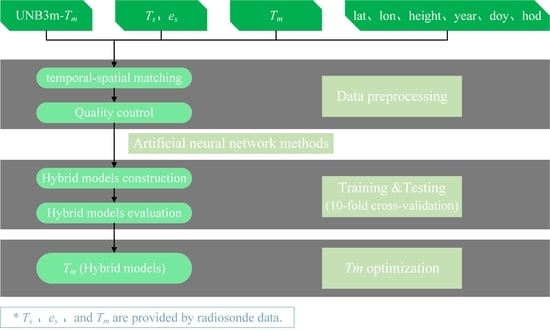
3. Construction of Hybrid Model
3.1. Three Artificial Neural Network Methods
3.1.1. BPNN
3.1.2. RF
3.1.3. GRNN
3.2. Evaluation Indicators Adopted by the Model
3.3. Parameter Determination
4. Performance Analyses of Hybrid Models
4.1. Overall Performance
4.2. Spatiotemporal Performance of the Hybrid Models
4.3. Occupancy of Hybrid Models
5. Applications of Hybrid Models in Retrieving PWV
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.H.; Zhang, L.Y. Climate applications of a global, 2-hourly atmospheric precipitable water dataset derived from IGS tropospheric products. J. Geod. 2009, 83, 209–217. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Luo, O.F. Variability and Climatology of PWV From Global 13-Year GPS Observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1918–1924. [Google Scholar] [CrossRef]
- Wang, J.; Balidakis, K.; Zus, F.; Chang, X.; Ge, M.; Heinkelmann, R.; Schuh, H. Improving the Vertical Modeling of Tropospheric Delay. Geophys. Res. Lett. 2022, 49, e2021GL096732. [Google Scholar] [CrossRef]
- Wang, X.M.; Zhang, K.F.; Wu, S.Q.; He, C.Y.; Cheng, Y.Y.; Li, X.X. Determination of zenith hydrostatic delay and its impact on GNSS-derived integrated water vapor. Atmos. Meas. Tech. 2017, 10, 2807–2820. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Yuan, Y.B.; Ou, J.K.; Chai, Y.J.; Li, Z.S.; Liou, Y.A.; Wang, N.B. New versions of the BDS/GNSS zenith tropospheric delay model IGGtrop. J. Geod. 2015, 89, 73–80. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. Gps Meteorology—Remote-Sensing of Atmospheric Water-Vapor Using the Global Positioning System. J. Geophys. Res.-Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Yu, S.W.; Liu, Z.Z. Temporal and Spatial Impact of Precipitable Water Vapor on GPS Relative Positioning During the Tropical Cyclone Hato (2017) in Hong Kong and Taiwan. Earth Space Sci. 2021, 8, e2020EA001371. [Google Scholar] [CrossRef]
- Zhao, Q.Z.; Liu, Y.; Ma, X.W.; Yao, W.Q.; Yao, Y.B.; Li, X. An Improved Rainfall Forecasting Model Based on GNSS Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4891–4900. [Google Scholar] [CrossRef]
- Zhang, H.X.; Yuan, Y.B.; Li, W.; Ou, J.K.; Li, Y.; Zhang, B.C. GPS PPP-derived precipitable water vapor retrieval based on T-m/P-s from multiple sources of meteorological data sets in China. J. Geophys. Res.-Atmos. 2017, 122, 4165–4183. [Google Scholar] [CrossRef]
- Wang, X.M.; Zhang, K.F.; Wu, S.Q.; Fan, S.J.; Cheng, Y.Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res.-Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, B.; Xu, C.; Yan, F. Improved one/multi-parameter models that consider seasonal and geographic variations for estimating weighted mean temperature in ground-based GPS meteorology. J. Geod. 2013, 88, 273–282. [Google Scholar] [CrossRef]
- Jin, S.G.; Li, Z.; Cho, J. Integrated Water Vapor Field and Multiscale Variations over China from GPS Measurements. J. Appl. Meteorol. Climatol. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Lee, S.W.; Kouba, J.; Schutz, B.; Kim, D.H.; Lee, Y.J. Monitoring precipitable water vapor in real-time using global navigation satellite systems. J. Geod. 2013, 87, 923–934. [Google Scholar] [CrossRef]
- Emardson, T.R.; Elgered, G.; Johansson, J.M. Three months of continuous monitoring of atmospheric water vapor with a network of Global Positioning System receivers. J. Geophys. Res.-Atmos. 1998, 103, 1807–1820. [Google Scholar] [CrossRef]
- Ross, R.J.; Rosenfeld, S. Estimating mean weighted temperature of the atmosphere for Global Positioning System applications. J. Geophys. Res.-Atmos. 1997, 102, 21719–21730. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.M.; Xu, T.H.; Nie, W.F.; Wang, J.; Xu, G.C. Establishment of atmospheric weighted mean temperature model in the polar regions. Adv. Space Res. 2020, 65, 518–528. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, N.S.; Zhang, K.F.; Liu, J.Y. A New Method for Refining the GNSS-Derived Precipitable Water Vapor Map. Sensors 2019, 19, 698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.H.; Yao, Y.B.; Sang, J.Z. A new weighted mean temperature model in China. Adv. Space Res. 2018, 61, 402–412. [Google Scholar] [CrossRef]
- Bohm, J.; Moller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Schuler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques. GPS Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Yao, Y.B.; Xu, C.Q.; Zhang, B.; Cao, N. GTm-III: A new global empirical model for mapping zenith wet delays onto precipitable water vapour. Geophys. J. Int. 2014, 197, 202–212. [Google Scholar] [CrossRef] [Green Version]
- Landskron, D.; Bohm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.Y.; Zhang, B.; Yao, Y.B. An ERA5-Based Model for Estimating Tropospheric Delay and Weighted Mean Temperature Over China With Improved Spatiotemporal Resolutions. Earth Space Sci. 2019, 6, 1926–1941. [Google Scholar] [CrossRef]
- Mateus, P.; Catalão, J.; Mendes, V.B.; Nico, G. An ERA5-Based Hourly Global Pressure and Temperature (HGPT) Model. Remote Sens. 2020, 12, 1098. [Google Scholar] [CrossRef] [Green Version]
- Mateus, P.; Mendes, V.B.; Plecha, S.M. HGPT2: An ERA5-Based Global Model to Estimate Relative Humidity. Remote Sens. 2021, 13, 2179. [Google Scholar] [CrossRef]
- Huang, L.K.; Liu, L.L.; Chen, H.; Jiang, W.P. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China. GPS Solut. 2019, 23, 51. [Google Scholar] [CrossRef]
- Yuan, Q.Q.; Xu, H.Z.; Li, T.W.; Shen, H.F.; Zhang, L.P. Estimating surface soil moisture from satellite observations using a generalized regression neural network trained on sparse ground-based measurements in the continental U.S. J. Hydrol. 2020, 580, 124351. [Google Scholar] [CrossRef]
- Shamshiri, R.; Motagh, M.; Nahavandchi, H.; Haghighi, M.H.; Hoseini, M. Improving tropospheric corrections on large-scale Sentinel-1 interferograms using a machine learning approach for integration with GNSS-derived zenith total delay (ZTD). Remote Sens. Environ. 2020, 239, 111608. [Google Scholar] [CrossRef]
- Li, L.; Xu, Y.; Yan, L.Z.; Wang, S.L.; Liu, G.L.; Liu, F. A Regional NWP Tropospheric Delay Inversion Method Based on a General Regression Neural Network Model. Sensors 2020, 20, 3167. [Google Scholar] [CrossRef]
- Ding, M.H. A neural network model for predicting weighted mean temperature. J. Geod. 2018, 92, 1187–1198. [Google Scholar] [CrossRef]
- Klos, A.; Hunegnaw, A.; Teferle, F.N.; Abraha, K.E.; Ahmed, F.; Bogusz, J. Statistical significance of trends in Zenith Wet Delay from re-processed GPS solutions. GPS Solut. 2018, 22, 51. [Google Scholar] [CrossRef] [Green Version]
- Mao, J.; Wang, Q.; Liang, Y.; Cui, T. A new simplified zenith tropospheric delay model for real-time GNSS applications. GPS Solut. 2021, 25, 43. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Academic Press: Cambridge, UK, 1992; pp. 65–93. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Yao, Y.B.; Sun, Z.Y.; Xu, C.Q. Establishment and Evaluation of a New Meteorological Observation-Based Grid Model for Estimating Zenith Wet Delay in Ground-Based Global Navigation Satellite System (GNSS). Remote Sens. 2018, 10, 1718. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Specht, D.F. A general regression neural network. IEEE Trans Neural Netw 1991, 2, 568–576. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. Improving the Estimation of Weighted Mean Temperature in China Using Machine Learning Methods. Remote Sens. 2021, 13, 1016. [Google Scholar] [CrossRef]
- Reich, S.L.; Gomez, D.R.; Dawidowski, L.E. Artificial neural network for the identification of unknown air pollution sources. Atmos. Environ. 1999, 33, 3045–3052. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Wang, J.H.; Zhang, L.Y.; Dai, A. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications. J. Geophys. Res.-Atmos. 2005, 110, D21101. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.-S. Real-time retrieval of precipitable water vapor from GPS precise point positioning. J. Geophys. Res.-Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]
- Chen, M. F-test and z-test for high-dimensional regression models with a factor structure. J. Stat. Comput. Simul. 2022, 1–20. [Google Scholar] [CrossRef]














| Input parameters | surface temperature (Ts), water vapor pressure (es), year, day of year (doy), and hour of day (hod), latitude, longitude, height, and UNB3m-Tm |
| Output parameter | Tm |
| Model | Hyperparameter | Bias (K) | MAE (K) | STD (K) | RMSE (K) | R | |
|---|---|---|---|---|---|---|---|
| UNB3m | - | - | −1.97 | 8.41 | 10.78 | 10.955 | 0.540 |
| Hm1 | Cross-V | 18 | 0.00 | 2.28 | 2.95 | 2.954 | 0.969 |
| Fitting | 18 | 0.00 | 2.28 | 2.95 | 2.953 | 0.969 | |
| Hm2 | Cross-V | 55 | 0.00 | 2.07 | 2.70 | 2.703 | 0.974 |
| Fitting | 55 | 0.00 | 1.62 | 2.10 | 2.096 | 0.984 | |
| Hm3 | Cross-V | 0.06 | 0.02 | 2.09 | 2.76 | 2.763 | 0.973 |
| Fitting | 0.06 | 0.01 | 1.59 | 2.10 | 2.101 | 0.984 | |
| Bevis | - | - | 0.80 | 3.53 | 4.49 | 4.563 | 0.931 |
| GPT3 | - | - | −0.48 | 3.35 | 4.31 | 4.340 | 0.932 |
| HGPT | - | - | 0.00 | 3.33 | 4.32 | 4.317 | 0.932 |
| Model | RMSE (K) |
|---|---|
| Hm1 | 2.954 |
| Hm2 | 2.703 |
| Hm3 | 2.763 |
| LS model | 3.340 |
| Bevis | 4.563 |
| GPT3 | 4.340 |
| HGPT | 4.317 |
| Model | Computer Storage Space | Number of Parameters |
|---|---|---|
| UNB3m | 104 KB | 103 |
| Hm1 | 104 KB | 104 |
| Hm2 | 104 KB | 104 |
| Hm3 | 104 KB | 104 |
| GPT3 | 29,081.6 KB | 324,003 |
| Station Number | Latitude/° | Longitude/° | Altitude/m |
|---|---|---|---|
| 58,457 | 30.23 | 120.16 | 43.1 |
| 50,557 | 49.16 | 125.23 | 242.6 |
| 51,463 | 43.78 | 89.61 | 921.4 |
| 45,004 | 22.33 | 114.17 | 66.17 |
| Station Number | Hm1 | Bevis | Change in | GPT3 | Change in | HGPT | Change in |
|---|---|---|---|---|---|---|---|
| MAE/mm | MAE/mm | % | MAE/mm | % | MAE/mm | % | |
| 58,457 | 0.150 | 0.224 | 49.3 | 0.332 | 121.2 | 0.332 | 121.2 |
| 50,557 | 0.067 | 0.134 | 99.8 | 0.137 | 104.2 | 0.157 | 133.5 |
| 51,463 | 0.080 | 0.169 | 112.0 | 0.166 | 108.2 | 0.154 | 92.5 |
| 45,004 | 0.169 | 0.381 | 124.7 | 0.307 | 81.3 | 0.308 | 82.0 |
| Station Number | Hm2 | Bevis | Change in | GPT3 | Change in | HGPT | Change in |
|---|---|---|---|---|---|---|---|
| RMSE/mm | RMSE/mm | % | RMSE/mm | % | RMSE/mm | % | |
| 58,457 | 0.199 | 0.293 | 46.9 | 0.430 | 115.4 | 0.428 | 114.4 |
| 50,557 | 0.101 | 0.182 | 80.6 | 0.204 | 102.5 | 0.240 | 137.8 |
| 51,463 | 0.111 | 0.248 | 124.5 | 0.217 | 96.5 | 0.206 | 86.1 |
| 45,004 | 0.219 | 0.454 | 107.1 | 0.380 | 73.3 | 0.379 | 72.6 |
| z (P) | Bevis | GPT3 | HGPT |
|---|---|---|---|
| Hm2 | −2.2463 (0.0122) | −2.7058 (0.003) | −2.6693 (0.004) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, M.; Li, J.; Liu, L.; Huang, L.; Zhou, L.; Huang, L.; He, H. Weighted Mean Temperature Hybrid Models in China Based on Artificial Neural Network Methods. Remote Sens. 2022, 14, 3762. https://doi.org/10.3390/rs14153762
Cai M, Li J, Liu L, Huang L, Zhou L, Huang L, He H. Weighted Mean Temperature Hybrid Models in China Based on Artificial Neural Network Methods. Remote Sensing. 2022; 14(15):3762. https://doi.org/10.3390/rs14153762
Chicago/Turabian StyleCai, Meng, Junyu Li, Lilong Liu, Liangke Huang, Lv Zhou, Ling Huang, and Hongchang He. 2022. "Weighted Mean Temperature Hybrid Models in China Based on Artificial Neural Network Methods" Remote Sensing 14, no. 15: 3762. https://doi.org/10.3390/rs14153762
APA StyleCai, M., Li, J., Liu, L., Huang, L., Zhou, L., Huang, L., & He, H. (2022). Weighted Mean Temperature Hybrid Models in China Based on Artificial Neural Network Methods. Remote Sensing, 14(15), 3762. https://doi.org/10.3390/rs14153762